Wenn ein Balken einer Biegebelastung ausgesetzt ist, beispielsweise durch das Anbringen einer Last an einem seiner Enden, beginnt er sich zu verformen. Die Biegelinie beschreibt dann die Form der resultierenden Krümmung des Balkens.
Die Biegelinie ist ein wichtiges Konzept in der Mechanik und wird verwendet, um die Deformationen von Bauteilen unter Biegebelastung zu analysieren und zu verstehen. Sie dient als Grundlage für die Berechnung von Spannungen, Verformungen und anderen wichtigen Eigenschaften von Bauteilen unter Biegebeanspruchung.
Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.
Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.
Biegelinie – Definition
Bei der Biegelinie handelt es sich um eine Funktion w(x), welche die Balkenbiegung durch äußere Querkräfte oder Momente angibt.
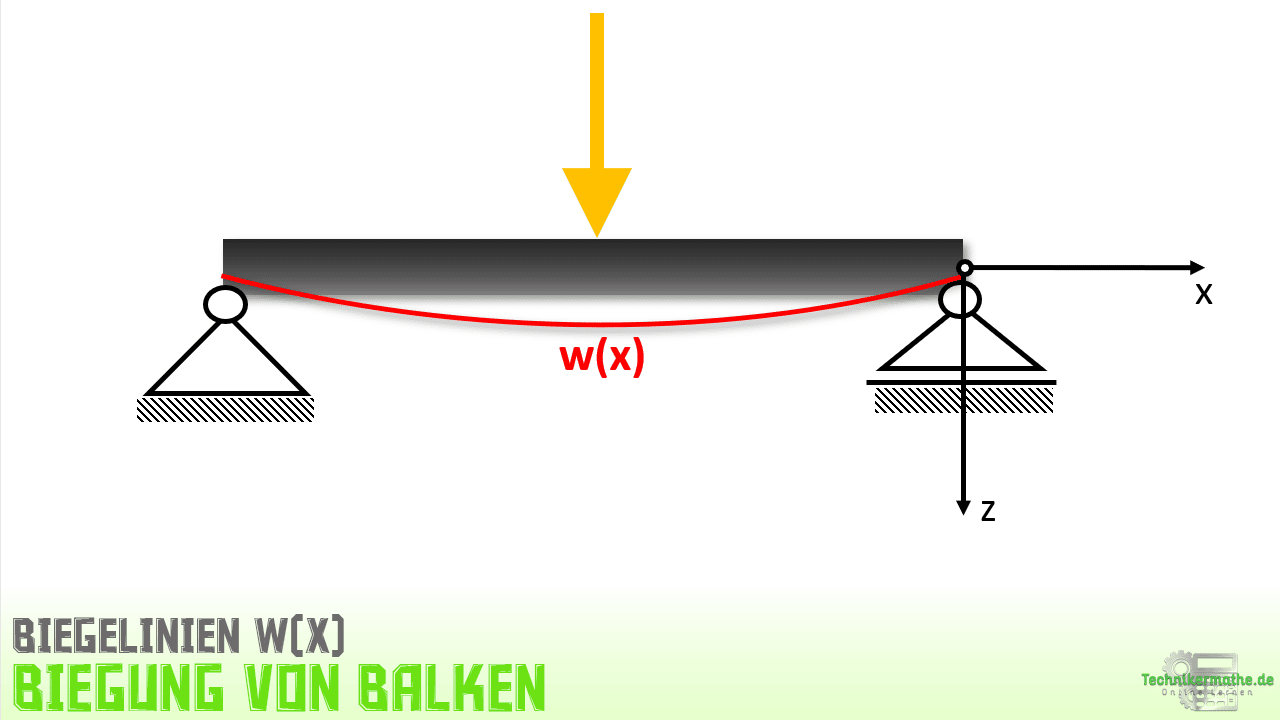
In der obigen Grafik siehst du einen Balken, der durch eine äußere Querkraft eine Durchbiegung in Richtung der z-Achse erfährt. Dabei wird die Durchbiegung in z-Richtung mit w(x) bezeichnet. Hierbei handelt es sich um eine Funktion in Abhängigkeit von x. Je nachdem an welcher Stelle die Durchbiegung des Balkens w(x) gesucht ist, kann dann für x einfach die gesuchte Stelle eingesetzt werden:
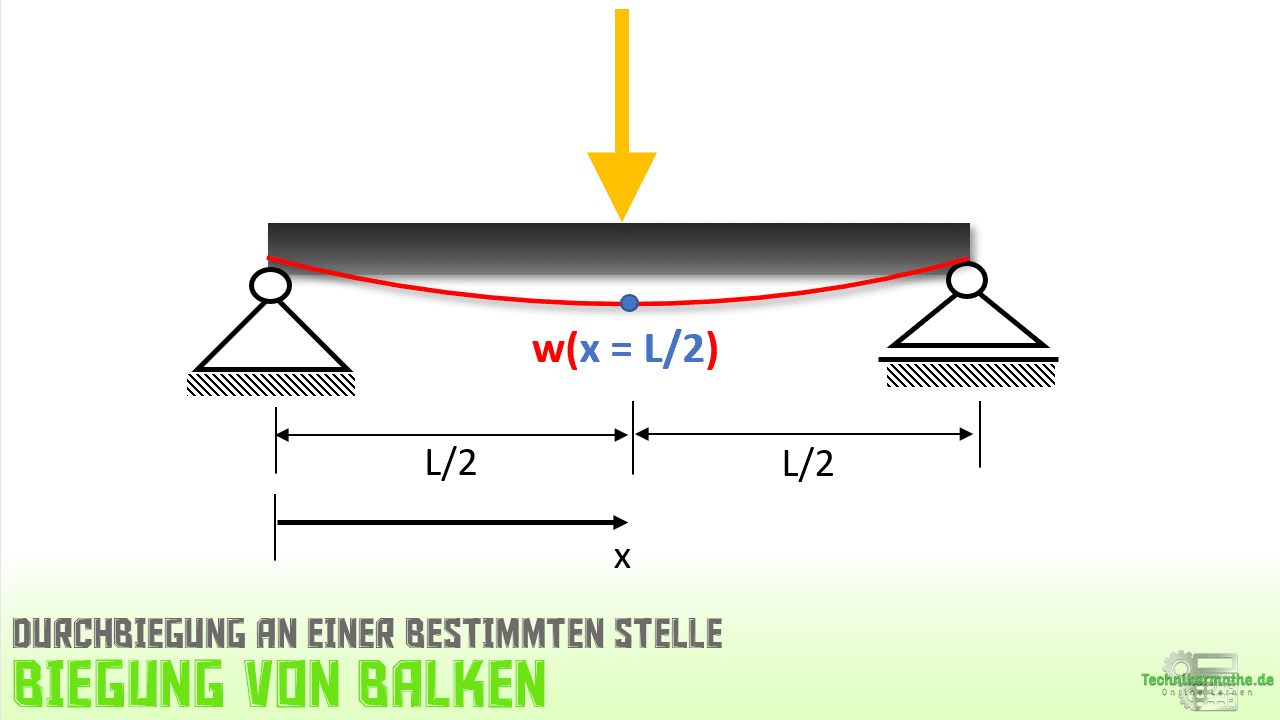
Schauen wir uns nun an, wie du die Biegelinie w(x) bestimmen kannst.
Biegelinie aus Momentenverlauf – Formeln
Für die Bestimmung Biegelinie w(x) bzw. für die Durchbiegung an einer bestimmten Stelle, kannst du die folgende Differentialgleichung 2. Ordnung verwenden:
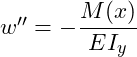
Hierbei ist E der Elastizitätsmodul (abhängig vom Werkstoff), Iy das Flächenträgheitsmoment bezüglich der y-Achse, w die gesuchte Durchbiegung und M(x) der Momentenverlauf.
Häufig wird aber anstelle des Elastizitätsmoduls gleich die Biegesteifigkeit EI angegeben.
Die obige Gleichung ist eine Differentialgleichung 2. Ordnung. Zweimaliges Integrieren führt hier auf die gesuchte Größe w. Bei der Integration fallen insgesamt zwei Integrationskonstanten an.
Vorgehensweise: Bestimmung der Biegelinie
Wir gehen nun wie folgt vor, um die Durchbiegung w aus der Differentialgleichung berechnen zu können:
- Wir bestimmen den Momentenverlauf im gesamten Balken (Schnittgröße!)
- Liegt eine veränderliche Biegesteifigkeit im Balken vor (ändert sich also der Querschnitt des Balkens), dann muss die Gleichung E(x)·I(x) aufgestellt werden.
- Wir bestimmen die Durchbiegung w(x) durch zweimalige Integration.
- Es fallen insgesamt 2 Integrationskonstanten an, die wir mittels Randbedingungen bestimmen.
- Bei mehr als einem Schnittbereich, müssen zusätzlich Übergangsbedingungen berücksichtigt werden.
Integration: Differentialgleichung der Biegelinie
Wir wollen uns schon im Vorfeld mal allgemein anschauen, wie die Integration der Differentialgleichung aussieht. Diese wird zweimal integriert. Nach jeder Integration fällt eine Integrationskonstante Ci an. Bei der zweiten Integration muss die Integrationskonstante C1 ebenfalls integriert werden.
Die zweifache Integration der Differentialgleichung sieht wie folgt aus:
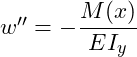
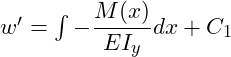
![Rendered by QuickLaTeX.com w = \int [\int -\dfrac{M(x)}{EI_y} dx] + C_1 \cdot x + C_2](https://technikermathe.de/wp-content/ql-cache/quicklatex.com-6fcfbf155aee0d71b1603bbd19555711_l3.png)
Für M(x) muss der Momentenverlauf eingesetzt werden.
Randbedingungen und Übergangsbedingungen
Nachdem die Integration durchgeführt wurde, müssen die Integrationskonstanten berechnet werden. Dafür benötigen wir die Randbedingungen an den Auflagern des Balkens, welche aus Tabellenwerken entnommen werden können. Außerdem müssen wir Übergangsbedingungen betrachten, wenn Gelenke bzw. Steifigkeitssprünge auftreten. In der nachfolgenden Lerneinheit findest du die Rand- und Übergangsbedingungen (auch als PDF), welche du bei der Bestimmung der Biegelinie bzw. Durchbiegung immer zur Hand haben solltest.
Betrachten wir hierzu das folgende Beispiel.
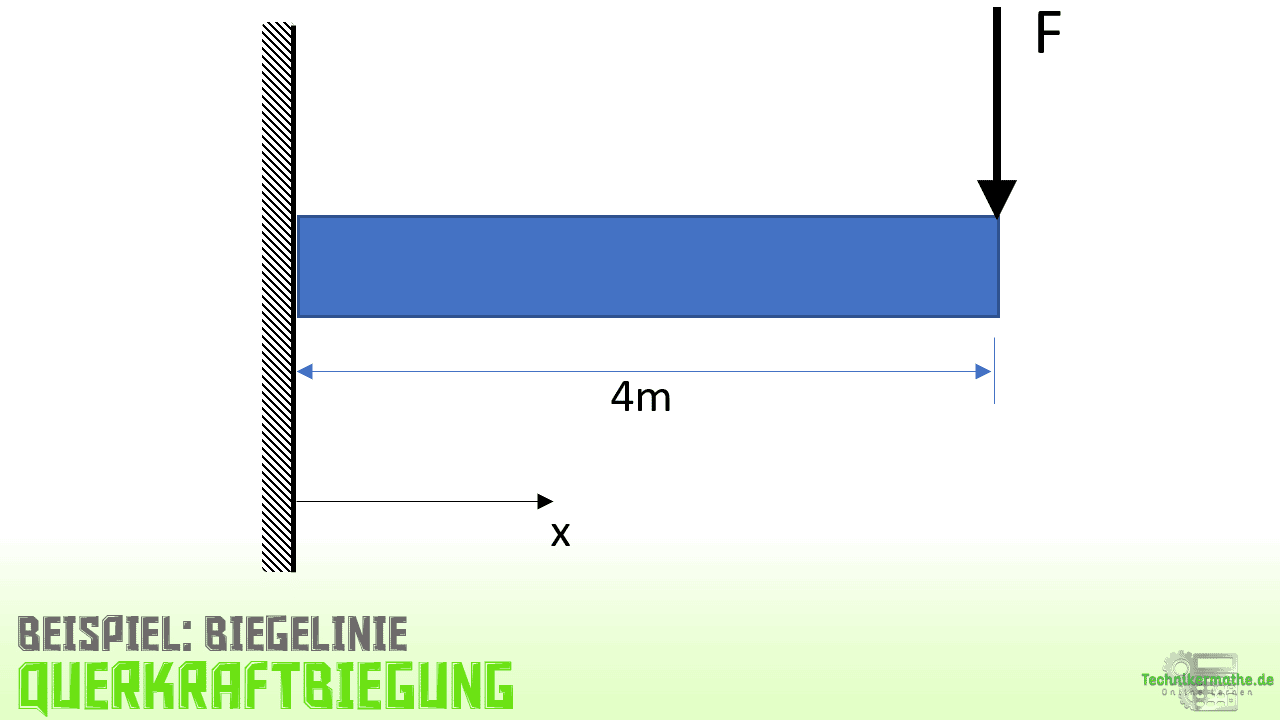
Beispiel 1: Biegelinie bei Querkraftbiegung
1.Auflagerkräfte berechnen

Zur Berechnung der Auflagerkräfte wenden wir die drei Gleichgewichtsbedingungen in der Ebene an.
Horizontale Gleichgewichtsbedingung
![]() :
:
![]()
Vertikale Gleichgewichtsbedingung
![]() :
:
![]()
![]()
Momentengleichgewichtsbedingung (Bezugspunkt Lager A)
![]() :
:
![]()
![]()
2. Momentenverlauf bestimmen
Zur Berechnung der Biegelinie benötigen wir den Momentenverlauf M(x). Wenn wir den obigen Balken betrachten, so ergibt sich genau ein Schnittbereich und damit auch eine Biegelinie.
Schnittbereich: 0 ≤ x ≤ 4m
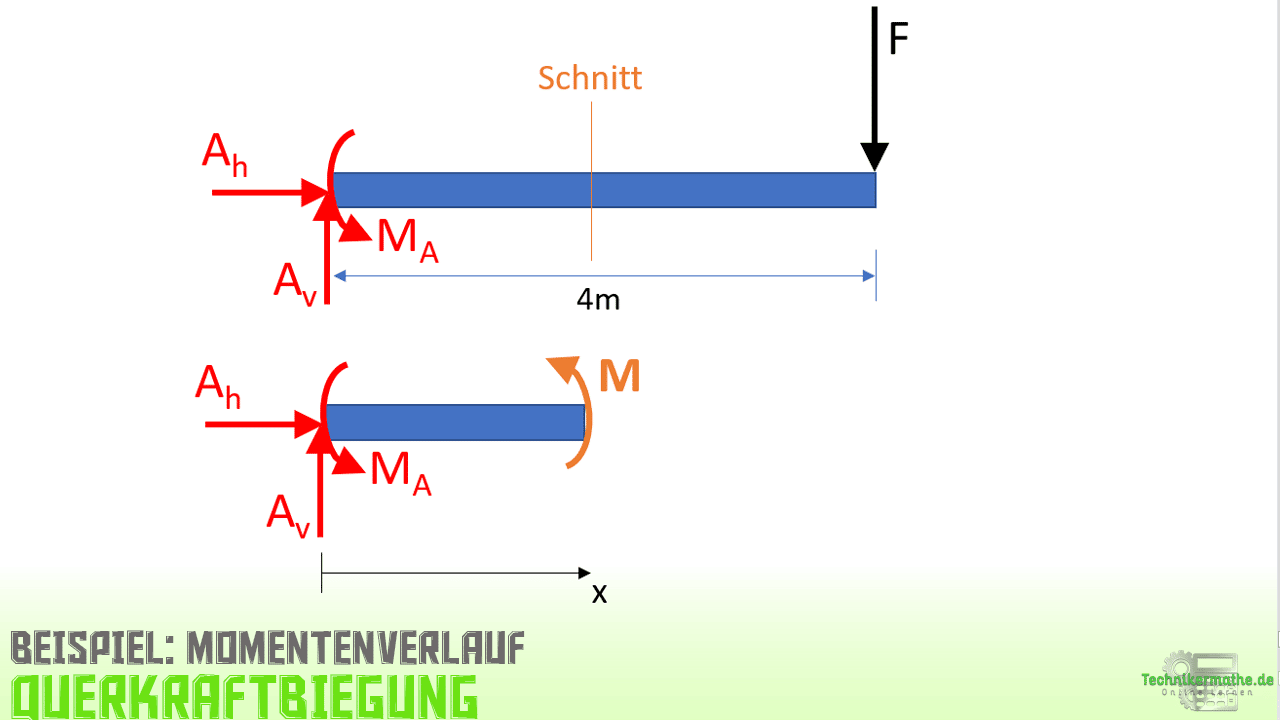
Wir berechnen den Momentenverlauf M. Dazu verwenden wir die Momentengleichgewichtsbedingung. Bei Berechnung von Schnittgrößen ist der Bezugspunkt immer der Schnitt:
![]()
![]()
![]()
Es handelt sich hierbei um einen linearen Momentenverlauf.
3. Biegelinie aus der Differentialgleichung bestimmen
Die Differentialgleichung zur Bestimmung der Biegelinie aus dem Momentenverlauf lautet:
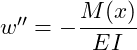
Da die Biegesteifigkeit EI im gesamten Balken konstant ist, können wir diese auch vor die Integration ziehen:
![]()
Wir integrieren somit den Momentenverlauf.
Biegelinie w
Wir starten damit die Biegelinie w zu bestimmen. Dazu betrachten wir unsere Differentialgleichung 2. Ordnung und integrieren diese zweimal, um die Biegelinie w zu bestimmen. Bei jeder Integration fallen zwei Integrationskonstanten an.
Wir starten mit der 1. Integration, bei welcher wir die 1. Ableitung der Biegelinie erhalten:
![]()
Einsetzen des Momentenverlaufs und Integration:
![]()
![]()
![]()
Wir führen die 2. Integration durch (die Integrationskonstante C1 muss ebenfalls mit integriert werden):
![]()
![]()
![]()
4. Integrationskonstante aus den Randbedingungen
Wir haben auf der linken Seite des Balkens eine feste Einspannung gegeben. Aus der vorherigen Seite können wir die Randbedingungen ablesen:
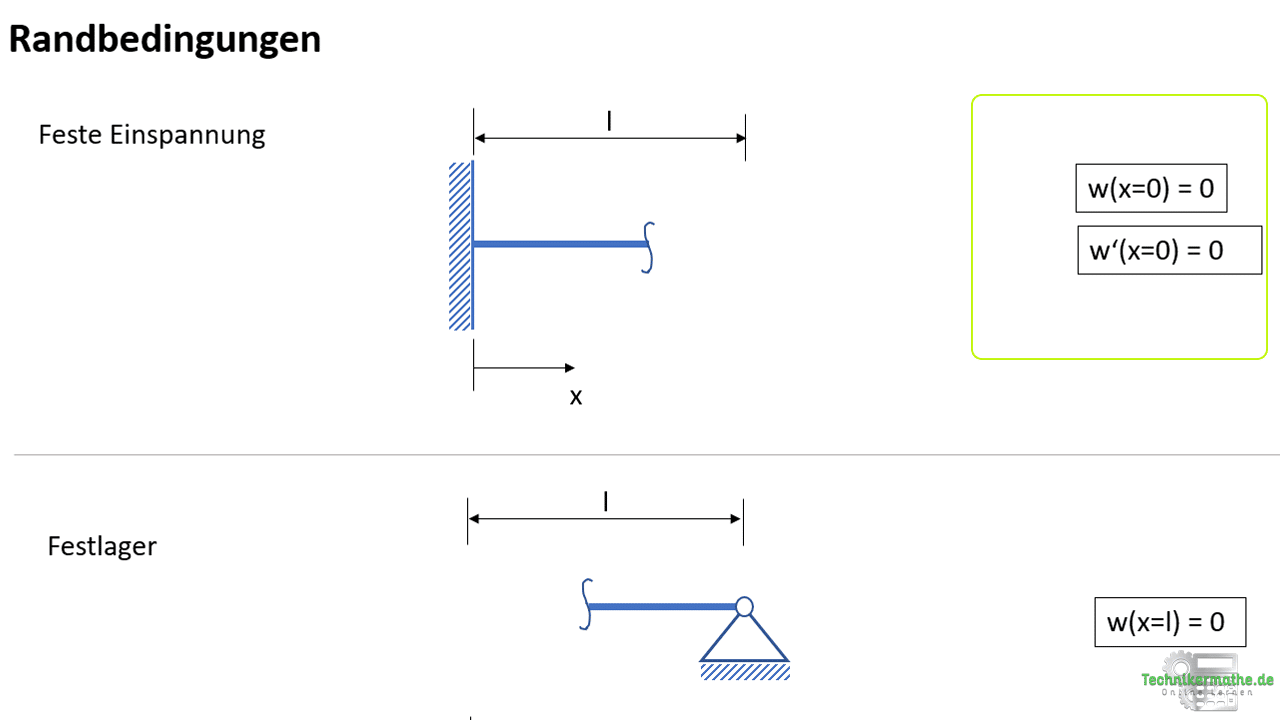
Dort wo eine feste Einspannung gegeben ist gilt w = 0 (die Durchbiegung ist an dieser Stelle also Null) & w’=0 (die erste Ableitung ist gleich Null bzw. die Steigung). Da die Einspannung an der linken Seite bei x = 0 gegeben ist gilt:
![]() Bei x = 0 (Ort der Einspannung) ist w = 0
Bei x = 0 (Ort der Einspannung) ist w = 0
![]() Bei x = 0 (Ort der Einspannung) ist w’ = 0
Bei x = 0 (Ort der Einspannung) ist w’ = 0
Wir setzen nun also in die 1. Ableitung (nach der 1. Integration) w’=0 und x = 0:
![]()
![]()
Damit haben wir die erste Integrationskonstante bestimmt:
![]()
Danach betrachten wir die Biegelinie und setzen w = 0, x = 0 und auch C1 = 0:
![]()
![]()
Die zweite Integrationskonstante ist ebenfalls Null:
![]()
Wir können im letzten Schritt die Biegelinie bestimmen, indem wir die berechneten Integrationskonstanten dort einsetzen:
![]()
![]()
![]()
Auflösen nach w:
![]()
Die Biegelinie ist bestimmt.
Ist noch der Wert der Biegesteifigkeit gegeben, so können wir diesen noch zusätzlich berücksichtigen. Nehmen wir eine Biegesteifigkeit von EI = 210.000 N mm² an, so ergibt sich:
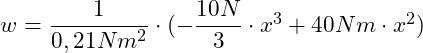
Die Biegesteifigkeit wurde hier von Nmm² in Nm² umgerechnet.
Nachdem wir uns mit der Biegelinie ausreichend befasst haben, wollen wir in der nächsten Lektion nochmals die Betrachtung vertiefen und den Umgang mit den Formeln verbessern.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team