TM2 – Prüfungsaufgabe: Normalspannung und Längenänderung [Beispiel, Berechnung]

In dieser Lerneinheit wollen wir uns eine Prüfungsaufgabe zur Bestimmung der Normalspannung und der Längenänderung eines rotierenden Stabs anschauen.

In dieser Lerneinheit betrachten wir eine Prüfungsaufgabe zur Bestimmung der Normalspannung und Längenänderung eines rotierenden Stabs.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM2 – Festigkeitslehre.

Rotierender Stab: Linienlast Formel

Bei einem rotierenden Stab mit der Winkelgeschwindigkeit $\omega$ , wirkt eine Belastung pro Längeneinheit n(x) auf den Stab. Diese können wir wie folgt berechnen:

$n(x) = \rho \cdot A \cdot x \cdot \omega^2$

mit

$\rho$ Dichte

$A$ Querschnitt

$x$ Betrachteter Schnitt im Abstand von der Drehachse

$\omega$ Winkelgeschwindigkeit

Mittels der obigen Formel ist es uns möglich die Normalspannung zu berechnen, die in einem rotierende Stab auftritt.

Prüfungsaufgabe: Normalspannung und Längenänderung

Aufgabenstellung

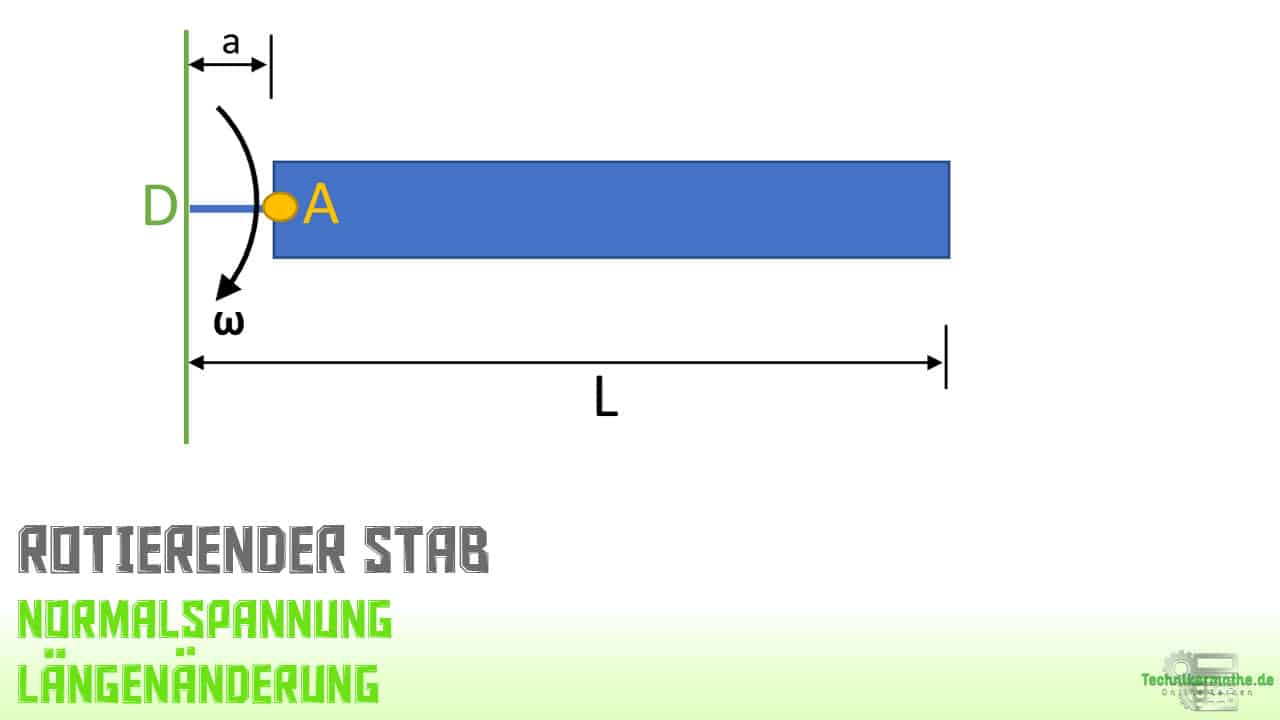
Rotierender Stab, Längenänderung, Normalspannung, Rotorblatt, Hubschrauber, Dehnung — Beispiel: Längenänderung und Normalspannung im Stab

Gegeben sei ein Rotorblatt eines Hubschraubers, der mit der Winkelgeschwindigkeit $\omega$ um den Punkt D rotiert. Für die Streckenlast, die durch das Rotieren im Rotorblatt auftritt, gilt die folgende Gleichung:

$n(x) = \rho \cdot A \cdot x \cdot \omega^2$

Die Querschnittsfläche A sei konstant!

Gegeben sind:

$L = 5m$

$a = 5cm$

$\rho = 4,4 · 10^{-6} \frac{kg}{mm^3}$

$\omega = 30 s^{-1}$

a) Bestimme die Normalspannung $\sigma_A$ an der Einspannung A!

b) Bestimme die Längenänderung ΔL!

Zunächst müssen wir die Einheiten in SI-Einheiten umrechnen:

$b = 5cm = 0,05m$

$\rho = 4,4 \cdot 10^{-6} \dfrac{kg}{mm^3} = 4,4 \cdot 10^{-6} \dfrac{kg}{10^{-9} m^3} = 4400 \dfrac{kg}{m^3}$

Wir suchen die Normalspannung. Diese können wir im Stab mittels der folgenden Gleichung bestimmen:

$\sigma = \dfrac{N}{A}$

Wir haben eine Linienlast $n(x)$ gegeben. Diese können wir wie folgt berechnen (siehe vorangegangene Lerneinheit):

$N' = -n(x)$

Die Ableitung der Normalkraft führt zur negativen Linienlast. Durch die einmalige Integration erhalten wir daraus die Normalkraft N:

$N = \int -n(x) \; dx$

Einsetzen der gegebenen Linienlast:

$N = \int -\rho \cdot A \cdot x \cdot \omega^2 \; dx$

Hierbei sind $\rho$ , $A$ und $\omega^2$ Konstanten. Diese können wir also vor das Integral ziehen:

$N = -\rho \cdot A \cdot \omega^2 \int_x^L x \; dx$

Die Grenzen verlaufen von x bis L. x ist hierbei die Stelle, für welche die Normalspannung bzw. Normalkraft bestimmt werden soll (ausgehend vom Drehpunkt). L ist dabei die Länge des Stabes bis hin zum Drehpunkt. Es wird also immer der Teil des Stabs betrachtet, welcher der Rotation ausgesetzt ist.

Auflösen des Integrals:

$N = -\rho \cdot A \cdot \omega^2 \cdot [\frac{1}{2} x^2]_x^L$

$N = -\rho \cdot A \cdot \omega^2 \cdot [\frac{1}{2} L^2 -\frac{1}{2} x^2 ]$

Die obige Gleichung zeigt den Normalkraftverlauf für einen Schnitt bei x an.

Wir suchen die Normalspannung und wenden dazu die folgende Formel an:

$\sigma = \dfrac{N}{A}$

Einsetzen des Normalkraftverlaufs:

$\sigma = \dfrac{-\rho \cdot A \cdot \omega^2 \cdot [\frac{1}{2} L^2 -\frac{1}{2} x^2]}{A}$ |A kürzt sich raus

$\sigma = -\rho \cdot \omega^2 \cdot [\frac{1}{2} L^2 -\frac{1}{2} x^2]$ Normalspannungsverlauf

Die obige Gleichung zeigt den Normalspannungsverlauf in Abhängigkeit von x an. x ist dabei die Stelle, für welche die Normalspannung bestimmt werden soll.

Wir können nun die Normalspannung an der Stelle x = a = 0,05m berechnen:

$\sigma = -4400 \frac{kg}{m^3} \cdot (30 s^{-1})^2 \cdot [\frac{1}{2} (5m)^2 -\frac{1}{2} (0,05m)^2]$

$\sigma = -4400 \frac{kg}{m^3} \cdot (30 s^{-1})^2 \cdot 12,5 m^2 = -49.500.000 Pa = -49,5 MPa$

Die Normalspannung an der Einspannung A beträgt 49,5 MPa! Das negative Vorzeichen zeigt an, dass es sich hier um eine Druckspannung handelt.

b) Bestimme die Längenänderung ΔL!

In diesem Aufgabenteil wollen wir die Längenänderung des Stabs bestimmen. Die Längenänderung können wir zum Beispiel aus der Dehnung wie folgt berechnen:

$\triangle l = \int \epsilon \;dx$

Und da wir oben bereits die Normalspannung bestimmt haben, können wir das Hook’sche Gesetz anwenden:

Hook’sche Gesetz

$\sigma = E \cdot \epsilon$

mit

$E$ Elastizitätsmodul

$\epsilon$ Dehnung

$\sigma$ Normalspannung

Lösen wir die obige Gleichung nach der Dehnung ε auf:

$\epsilon = \dfrac{\sigma}{E}$

Einsetzen in die Formel für die Längenänderung:

$\triangle l = \int \dfrac{\sigma}{E} \;dx$

Der Elastizitätsmodul ist konstant, weshalb wir diesen vor das Integral ziehen:

$\triangle l = \dfrac{1}{E} \int \sigma \;dx$

Den Normalspannungsverlauf haben wir bereits im Aufgabenteil a) bestimmt:

$\triangle l = -\dfrac{1}{E} \cdot \int_a^L \rho \cdot \omega^2 \cdot [\frac{1}{2} L^2 -\frac{1}{2} x^2] \;dx$

Die Grenzen sind hier zwar identisch, allerdings ist dies nur der Aufgabenstellung geschuldet. Beim Aufgabenteil a) musst du für x die Stelle wählen, an welcher du die Normalspannung bestimmen möchtest. Dies war bei x = a. Bei der Längenänderung betrachten wir hingegen den gesamten Stab (hier: Rotorblatt). Dieses beginnt bei der Einspannung, also bei x = a und endet bei x = L. Deswegen sind die Grenzen in diesem Fall identisch!

Wir nehmen als nächstes die Integration vor:

$\triangle l = \dfrac{1}{E} \cdot \rho \cdot \omega^2 \cdot [\frac{1}{2} L^2 \cdot x -\frac{1}{6} x^3 ]_a^L$

Einsetzen der Grenzen (obere minus untere Grenze):

$\triangle l = \dfrac{1}{E} \cdot \rho \cdot \omega^2 \cdot [\frac{1}{2} L^2 \cdot L -\frac{1}{6} L^3 - (\frac{1}{2} L^2 \cdot a -\frac{1}{6} a^3)]$

Zusammenfassen:

$\triangle l = \dfrac{1}{E} \cdot \rho \cdot \omega^2 \cdot [\frac{1}{2} L^3 -\frac{1}{6} L^3 - \frac{1}{2} L^2 \cdot a +\frac{1}{6} a^3)]$

$\triangle l = \dfrac{1}{E} \cdot \rho \cdot \omega^2 \cdot [\frac{1}{3} L^3 - \frac{1}{2} L^2 \cdot a +\frac{1}{6} a^3)]$

Einsetzen der gegebenen Werte:

$\triangle l = \dfrac{1}{110000 \cdot 10^6 Pa} \cdot 4400 \frac{kg}{m^3} \cdot (30 \frac{1}{s})^2 \cdot [\frac{1}{3} (5m)^3 - \frac{1}{2} (5m)^2 \cdot 0,05m +\frac{1}{6} (0,05m)^3)]$

$\triangle l =0,001478m = 1,478mm$

Hier sind die Grenzen von a bis L zu setzen, weil wir die Längenänderung im Rotorblatt suchen. Dieses startet erst bei x = a und endet bei x = L.

Die Längenänderung beträgt 1,478mm.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++