Fachwerke sind eine spezielle Bauweise von Tragwerken, die sich durch ihre offene Struktur aus senkrechten und waagerechten Balken auszeichnen, die miteinander verbunden sind. Diese Bauweise wurde seit dem Mittelalter verwendet und findet auch heute noch in verschiedenen Formen Anwendung, besonders in Brücken, Dachstühlen und Gebäudefassaden.
Der Aufbau eines Fachwerks besteht aus vertikalen Ständern, horizontalen Riegeln und schrägen Streben, die miteinander zu einem stabilen Gerüst verbunden sind. Die vertikalen Ständer tragen die vertikalen Lasten, während die horizontalen Riegel die Horizontallasten aufnehmen. Die schrägen Streben dienen dazu, die Kräfte abzuleiten und das Fachwerk zu stabilisieren.
Wir wollen in dieser Lerneinheit den Aufbau von Fachwerken betrachten und gehen hier speziell auf die Abzählformel sowie auf das 1., 2. und 3. Bildungsgesetz ein.
Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs: TM1-Statik

Ein Fachwerk ist eine Tragkonstruktion aus Profilstäben (siehe obige Grafik: Baukran). Auch Hochspannungsmasten sind Fachwerkskonstruktionen. Fachwerke bieten den Vorteil eines minimalem Materialaufwands bei maximaler Stabilität. Durch Fachwerke wird demnach Material eingespart, was zu einem geringeren Gewicht solcher Konstruktionen führt. Wie du bereits jetzt erlesen kannst, sind Fachwerke sehr vorteilhaft gegenüber anderen Konstruktionsvarianten.
Fachwerke – Aufbau
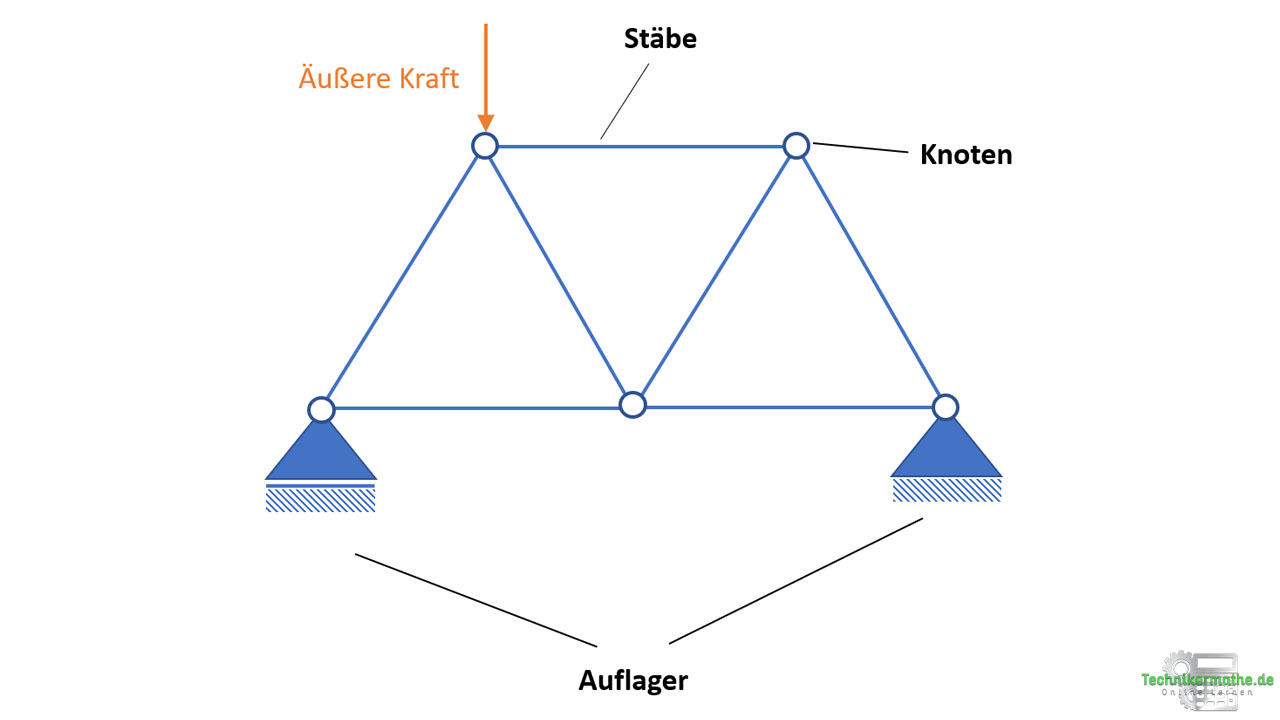
Die Verbindungsstellen der einzelnen Stäbe eines Fachwerks werden als Knoten bezeichnet. Wir gehen davon aus, dass die Knoten keine Momente übertragen, was dazu führt, dass die Stäbe nur Druck- bzw. Zugkräfte übertragen und keine Biegekräfte, Torsionskräfte oder Scherkräfte. Damit können die Knoten als Gelenke angesehen werden.
Jeder Knoten befindet sich im Gleichgewicht, d.h. das für jeden Knoten die Gleichgewichtsbedingungen in x- und y-Richtung angewendet werden können.
Die Wirkungslinien der Stabkräfte verlaufen in den Stabachsen und entsprechen demnach den Richtungen der Stäbe. Unbekannt sind die Beträge der einzelnen Stabkräfte und ob es sich um Zug- oder Druckstäbe handelt.
Mithilfe des Knotenpunktverfahrens und des Ritterschnittverfahrens können diese unbekannten Größen bestimmt werden. Wie das funktioniert zeigen wir dir in den folgenden beiden Lerneinheiten.
Freiheitsgrade von Knoten
Unter Freiheitsgraden verstehen wir Bewegungsmöglichkeiten von Körpern in der Ebene.
Es gibt in der Ebene insgesamt drei Freiheitsgrade:
- Die Verschiebung in x-Richtung
- Die Verschiebung in y-Richtung
- Die Drehung in der x,y-Ebene
Freiheitsgrade werden mit einem kleinen Buchstaben f angegeben.
Wenn wir uns nun auf die Knoten eines Fachwerks beziehen, dann wirken in diesen – wie oben bereits erwähnt – keine Momente. Damit reduzieren sich die Freiheitsgrade von Knoten eines Fachwerks auf zwei (f = 2). Der Knoten eines Fachwerks kann sich demnach nur in x-Richtung und in y-Richtung verschieben.
Damit diese Verschiebung der Knoten verhindert wird, werden Stäbe und Auflager benötigt.
Statische Bestimmtheit: Abzählformel
Ein Fachwerk ist statisch bestimmt, wenn jede Bewegungsmöglichkeit genau durch eine Lager- oder Stabkraft unterbunden wird. Ist dies der Fall, so ist die Anzahl der unbekannten Lager- und Stabkräfte gleich der Anzahl der möglichen Bewegungen.
Mithilfe der Abzählformel kannst du ein Fachwerk auf statische Bestimmtheit hin überprüfen. Diese in Grundvoraussetzung dafür, dass alle Lager- und Stabkräfte mittels Gleichgewichtsbedingungen berechnet werden können:
![]()
mit
![]() = Anzahl der Auflagerkräfte
= Anzahl der Auflagerkräfte
![]() = Anzahl der Stabkräfte
= Anzahl der Stabkräfte
![]() = Anzahl der Knoten
= Anzahl der Knoten
Für jeden Knoten stehen 2 Gleichgewichtsbedingungen (x- und y-Richtung) zur Verfügung. Diese Anzahl multipliziert mit der Anzahl der Knoten k ergibt die Anzahl der Gleichgewichtsbedingungen (2k) die zur Verfügung stehen, um die unbekannten Lager- und Stabkräfte (a + s) zu berechnen.
Die obige Gleichung muss Null (f = 0) ergeben, damit das Fachwerk statisch bestimmt ist, denn dann entspricht die Anzahl der Gleichgewichtsbedingungen der Anzahl der Lager- und Stabkräfte.
Der Vollständigkeit halber wollen wir hier aber auch noch angeben, was passiert, wenn die Abzählformel nicht den Wert Null annimmt:
![]() statisch unbestimmt
statisch unbestimmt
Ist f > 0, dann ist das Fachwerk statisch unbestimmt (bzw. statisch überbestimmt). Die Anzahl der Lager- und Stabkräfte übersteigt die Anzahl der möglichen Bewegungen. Mindestens einer Bewegungsmöglichkeit wirkt mehr als eine Kraft entgegen. In diesem Fall können die unterschiedlichen Kräfte nicht mithilfe der Gleichgewichtsbedingungen ermittelt werden.
![]() kinematisch
kinematisch
Ist f < 0, dann ist das Fachwerk kinematisch. Die Anzahl der Lager- und Stabkräfte ist kleiner als die Anzahl der möglichen Bewegungen. Mindestens einer Bewegungsmöglichkeit wirkt demnach keine Kraft entgegen, d.h. der Knoten kann sich (infinitesimal) verschieben. Die Stab- und Lagerkräfte können zwar berechnet werden, jedoch kann ein solches System nicht bestehen.
Die Abzählformel ist ein notwendiges aber kein hinreichendes Kriterium, um herauszufinden, ob ein System tatsächlich statisch bestimmt ist. Denn auch ein nach der Abzählformel ermitteltes statisch bestimmtes System kann kinematisch sein. Um sicherzustellen, dass es sich um ein statisch bestimmtes System handelt, müssen also zusätzlich die Bildungsgesetze und der Polplan herangezogen werden.
Statische Bestimmtheit: Bildungsgesetze
Die im Weiteren behandelten Fachwerke sollen statisch bestimmt und damit nicht verschieblich sein. Zur Überprüfung der statischen Bestimmtheit eines Fachwerks stehen dir die nachfolgenden drei Bildungsgesetze zur Verfügung.
1. Bildungsgesetz
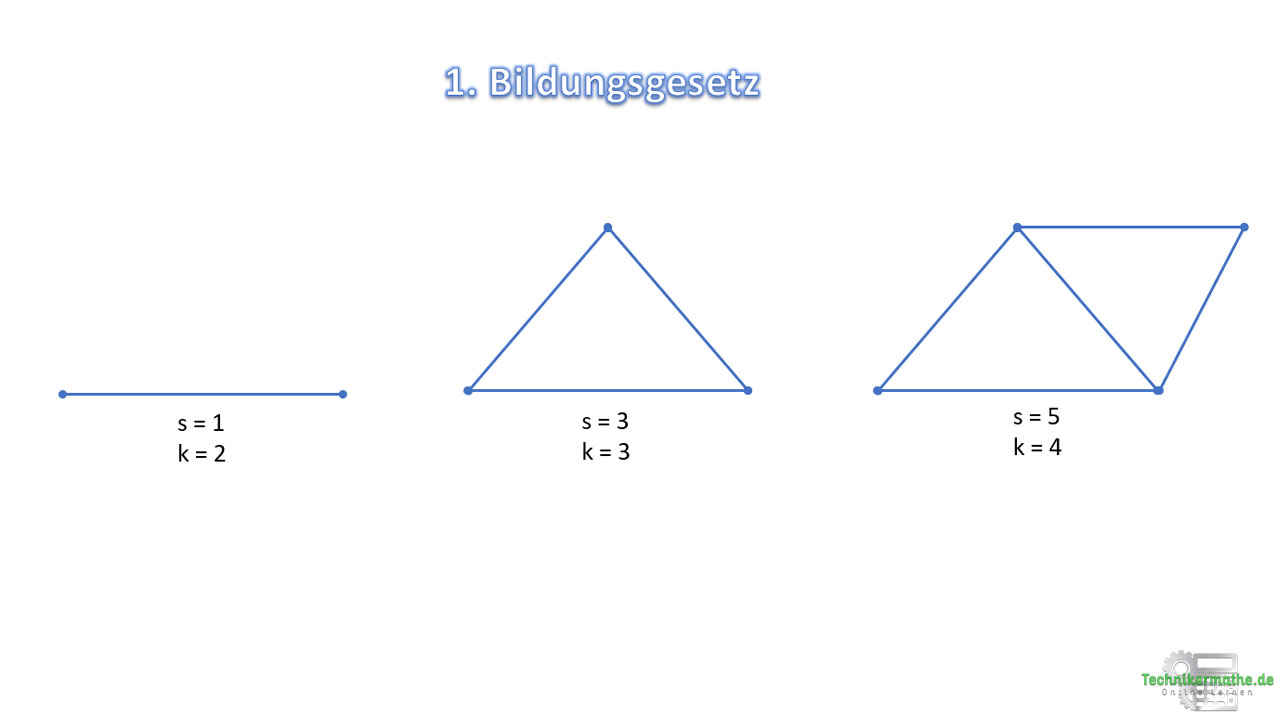
Ausgehend von einem Einzelstab werden zwei weitere Stäbe so an diesen Stab angefügt, dass ein Dreieck entsteht. Es entsteht so ein neuer Knoten. Es können nun je zwei weitere Stäbe an zwei beliebige Knoten angeschlossen und verbunden werden, ohne dass die beiden Stäbe auf einer Wirkungslinie liegen. Die Anzahl der Knoten erhöht sich beim Zufügen von zwei Stäben immer um eins.
Diese Vorgehensweise kann beliebig fortgesetzt werden. Ein Fachwerk, welches nach diesem Muster aufgebaut ist, heißt einfaches Fachwerk. Hier gilt die obige Beziehung:
![]()
2. Bildungsgesetz
Zwei nach dem ersten Bildungsgesetz aufgebaute Fachwerke können wie folgt miteinander verbunden werden:
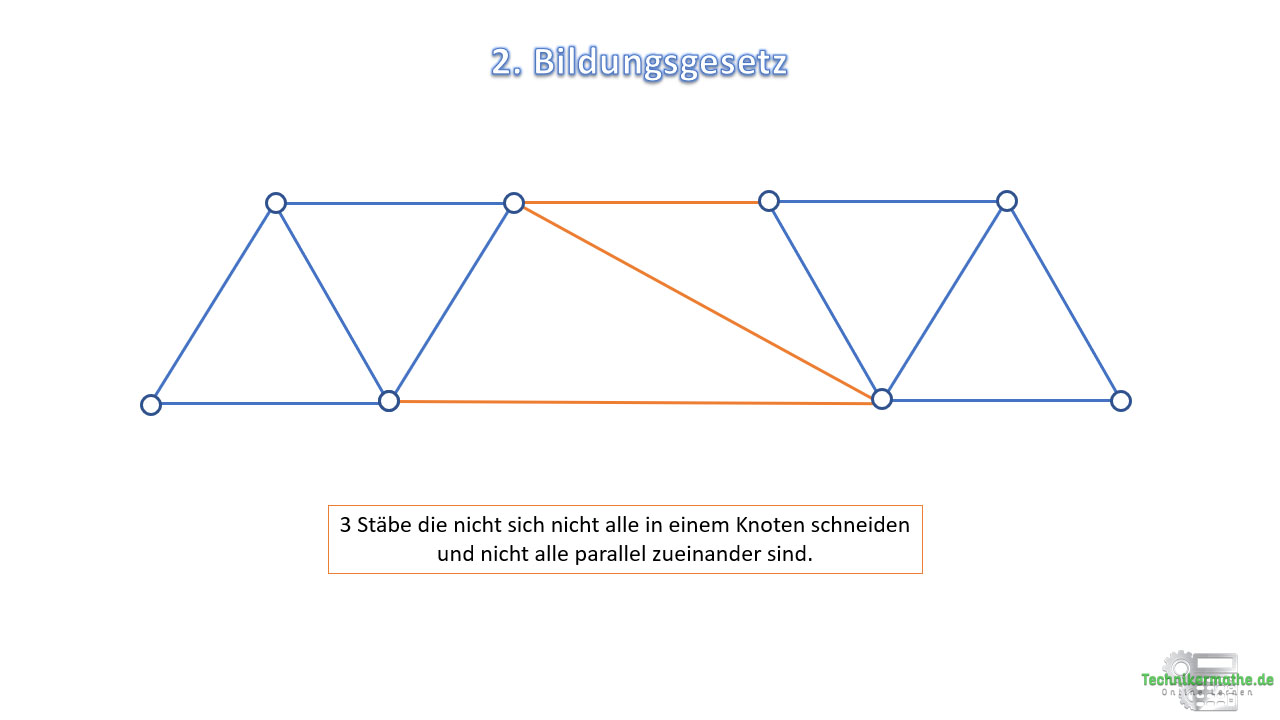
Durch drei Stäbe, die sich nicht alle in einem Punkt scheiden und die nicht alle parallel sind.
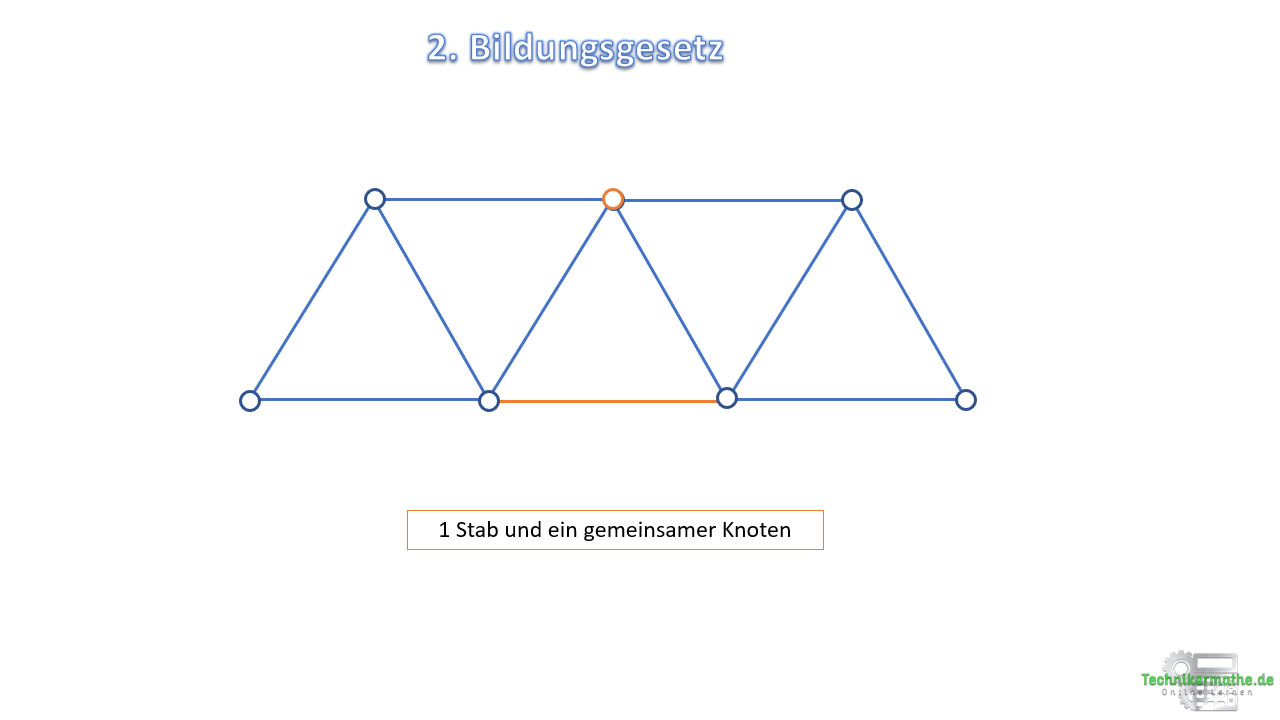
Durch einen gemeinsamen Knoten und einen Stab.
3. Bildungsgesetz
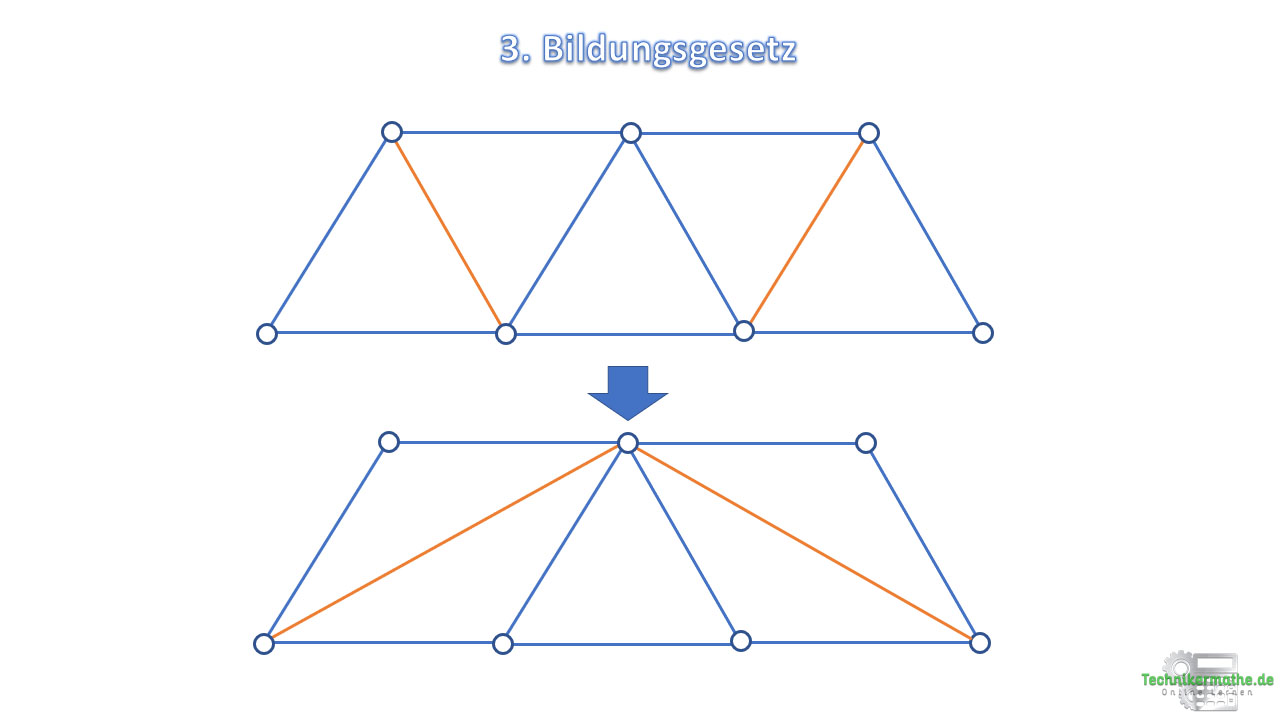
Wird ein Stab aus einem Fachwerk (nach dem 1. und 2. Bildungsgesetz) entfernt, so muss an einer anderen Stelle ein Stab so eingefügt werden, dass das Fachwerk wieder dem 1. und 2. Bildungsgesetz entspricht.
Nachdem du weißt, wie du die statische Bestimmtheit mittels Abzählformel bzw. Bildungsgesetz überprüfen kannst, wollen wir uns im folgenden mit der Berechnung der unbekannten Stabkräfte eines Fachwerks beschäftigen und gehen dabei immer von statisch bestimmten Systemen aus. Wir starten mit dem Knotenpunktverfahren.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






