TM1 – Schnittgrößen bei konstanter Streckenlast [Definition, Aufgabe, Videos, Lösung]

Die Schnittgrößen sind nichts anderes als die Resultierende der Spannungen im Inneren des Balkens. Diese inneren Spannungen treten auf, wenn Kräfte von außen auf den Balken wirken. Ein solcher äußerer Krafteinfluss kann zum Beispiel eine Schneelast sein, die dann keine Einzelkraft mehr ist, sondern eine Streckenlast, also eine Last, die über einen bestimmten Bereich auf den Balken wirkt.

In dieser Lerneinheit berechnen wir die Schnittgrößen bei konstanter Streckenlast (auch: rechteckiger Streckenlast) und zeigen dir die Schnittgrößenverläufe auf.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM1-Statik.

Für ein optimales Verständnis helfen dir zwei ausführliche Videoclips und ein anschauliches Rechenbeispiel zu dem Thema.

Videos – Schnittgrößen bei konstanter Streckenlast

In den folgenden Videos zeigen wir dir ausführlich, wie du die Auflagerkräfte und die Schnittgrößen bei einer gegebenen konstanter Streckenlast bestimmst.

1.Teil: Auflagerkräfte berechnen:

2. Teil: Schnittgrößen berechnen:

rechteckige Streckenlast, konstante Streckenlast, Schnittgrößen

Bevor wir mit der Berechnung der Schnittgrößen bei konstanter Streckenlast beginnen, wollen wir uns zunächst einmal anschauen was eine Streckenlast ist und wie du die Resultierende der Streckenlast bildest.

Rechteckige bzw. konstante Streckenlast

Eine Streckenlast ist dann gegeben, wenn verteilte Kräfte auf eine Linie oder Fläche wirken. Zum besseren Verständnis stelle dir ganz einfach eine Schneedecke auf einer Brücke vor. Diese Schneedecke ist annähernd an jedem Punkt der Brücke gleich dick und über die gesamte Brücke gleich verteilt.

Streckenlast, konstante Streckenlast, rechteckige Streckenlast, Schnittgrößen — Streckenlast: Schneedecke, Schnittgrößen bei konstanter Streckenlast

In der obigen Grafik ist eine konstante Streckenlast gegeben. Diese zeichnet sich dadurch aus, dass die Größe der Einzelkraft an jeder Stelle gleich ist. Damit wirkt auf das betrachtete Bauteil an jeder Stelle die gleiche Kraft. Eine konstante Streckenlast weist eine rechteckige Fläche auf, weshalb auch häufig von einer rechteckigen Streckenlast gesprochen wird.

Wir wollen nun zeigen, wie die Schnittgrößen berechnet werden, wenn eine konstante Streckenlast wirkt.

Resultierende der konstanten Streckenlast

Willst du die Schnittgrößen in einem Balken berechnen, so musst du zunächst die Auflagerkräfte ermitteln. Um die Auflagerkräfte ermitteln zu können, musst du zunächst die Resultierende der gegebenen Streckenlast bestimmen.

Die Resultierende der Streckenlast ist nichts anderes als der Flächeninhalt der gegebenen Streckenlast. Die Resultierende greift im Schwerpunkt der gegebenen Fläche an.

Schauen wir uns dazu mal die folgende Grafik an:

Streckenlast, konstante Streckenlast, rechteckige Streckenlast, Resultierende, Schwerpunkt — Resultierende der konstanten Streckenlast, Schnittgrößen bei konstanter Streckenlast

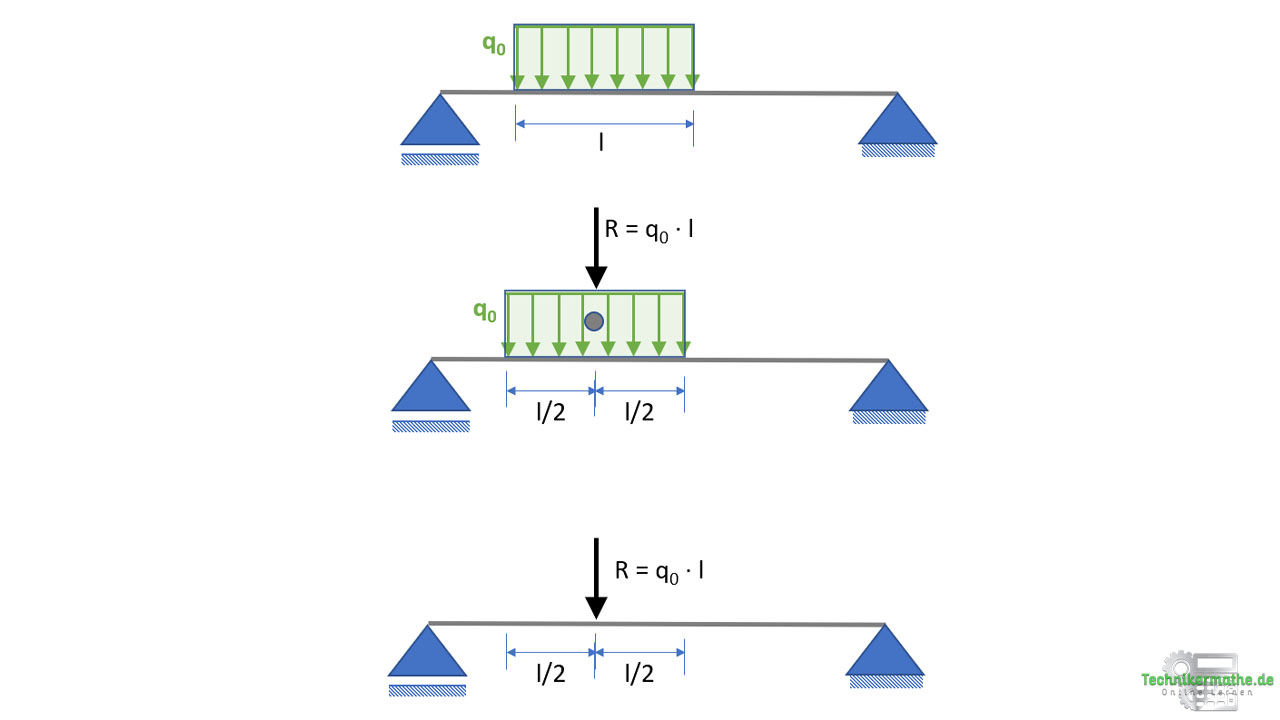
Ist eine rechteckige Streckenlast gegeben, so berechnen wir zur Bestimmung der Resultierenden den rechteckigen Flächeninhalt. Der Flächeninhalt eines Rechtecks bestimmt sich durch Höhe mal Länge. Für die rechteckige Streckenlast gilt also:

Resultierende einer konstanten Streckenlast

$R = q_0 \cdot l$

mit

$q_0$ Einzellast

$l$ Länge der Streckenlast

Wir wollen noch wissen, wo genau die Resultierende am Balken angreift. Die Resultierende einer Streckenlast greift immer im Schwerpunkt der Fläche an. Wir haben hier eine rechteckige Fläche gegeben. Bei einem Rechteck liegt die Schwerpunkt genau in der Mitte der Fläche. Da uns nur der horizontale Abstand interessiert, greift die Resultierende also bei der Hälfte der Länge der Streckenlast (l/2) an.

Merk’s dir!

Die Resultierende der Streckenlast ersetzt die Streckenlast. Du musst nun nicht extra eine neue Skizze anfertigen und den Balken ohne Streckenlast skizzieren. Du kannst statt dessen auch einfach die Resultierende oberhalb der Streckenlast einzeichnen, so wie am mittleren Balken gezeigt.

Wir wollen uns das Vorgehen aber auch nochmal an einem weiteren Beispiel anschauen.

Beispiel: Schnittgrößen bei konstanter Streckenlast

Schnittgrößen, Rechteckige Streckenlast, konstante Streckenlast, Beispiel Schnittgrößen, schräger Kraft, Beispiel — Beispiel: Schnittgrößen bei konstanter Streckenlast

Beispiel: Schnittgrößen bei rechteckiger Streckenlast

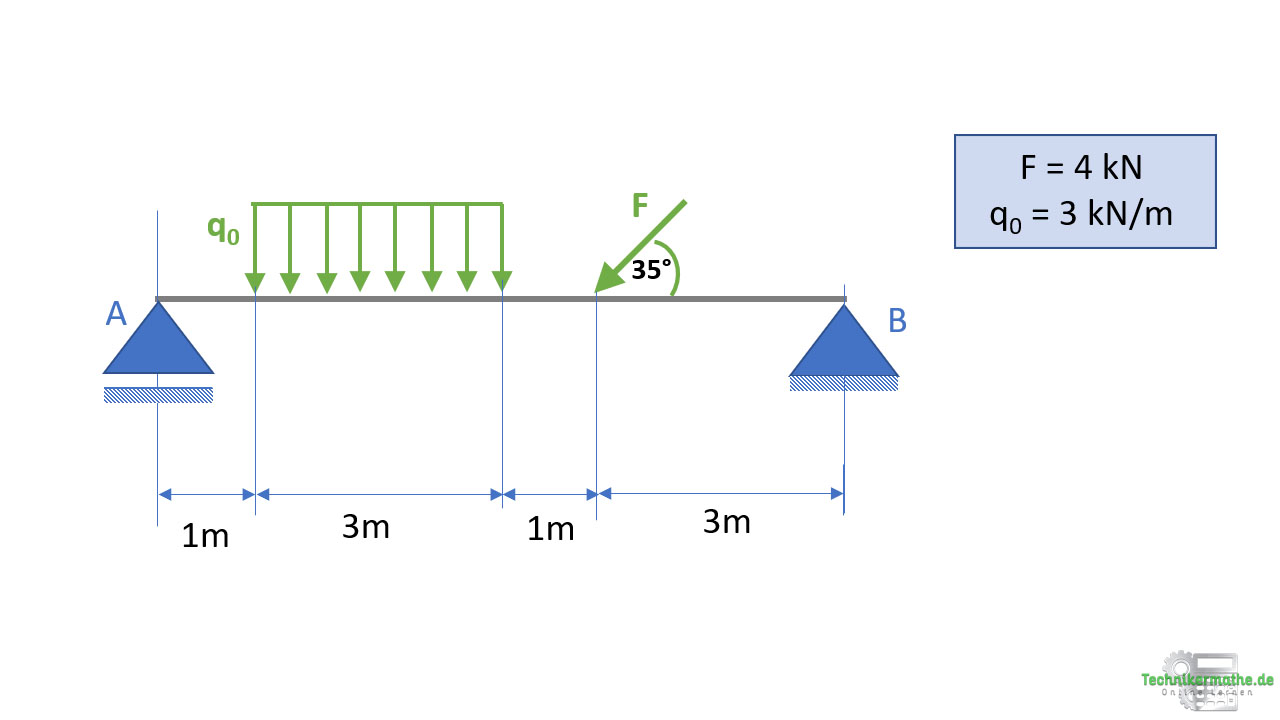
Gegeben sei der obige Balken, an welchen eine rechteckige Streckenlast mit q₀ = 3 kN/m sowie eine Kraft F = 4 kN mit einem Winkel von 35° zur Horizontalen angreift.

Wir wollen für den gesamten Balken die Schnittgrößen bestimmen und die Schnittgrößenverläufe angeben.

Kräftezerlegung durchführen

Zunächst führen wir eine Kräftezerlegung der äußeren Kraft F durch:

$F_x = F \cdot \cos(35^{\circ}) = 4 kN \cdot \cos(35^{\circ}) = 3,28 kN$

$F_y = F \cdot \sin(35^{\circ}) = 4 kN \cdot \sin(35^{\circ}) = 2,29 kN$

Resultierende der Streckenlast bilden

Als nächstes bilden wir die Resultierende der konstanten Streckenlast, um die Auflagerkräfte berechnen zu können. Dazu berechnen wir ganz einfach den Flächeninhalt der gegebenen konstanten Streckenlast:

$R = q_0 \cdot l = 3 \frac{kN}{m} \cdot 3m = 9 kN$

Der Angriffspunkt der Resultierenden ist immer im Schwerpunkt der Fläche. Da wir eine rechteckige Fläche gegeben haben, liegt der Schwerpunkt genau in der Mitte. Somit greift die Resultierende bei der Hälfte der Länge (1,5m) der Streckenlast an.

Schnittgrößen, rechteckige Streckenlast, konstante Streckenlast, Auflagerkräfte, Resultierende — Resultierende der Streckenlast, Schnittgrößen bei konstanter Streckenlast

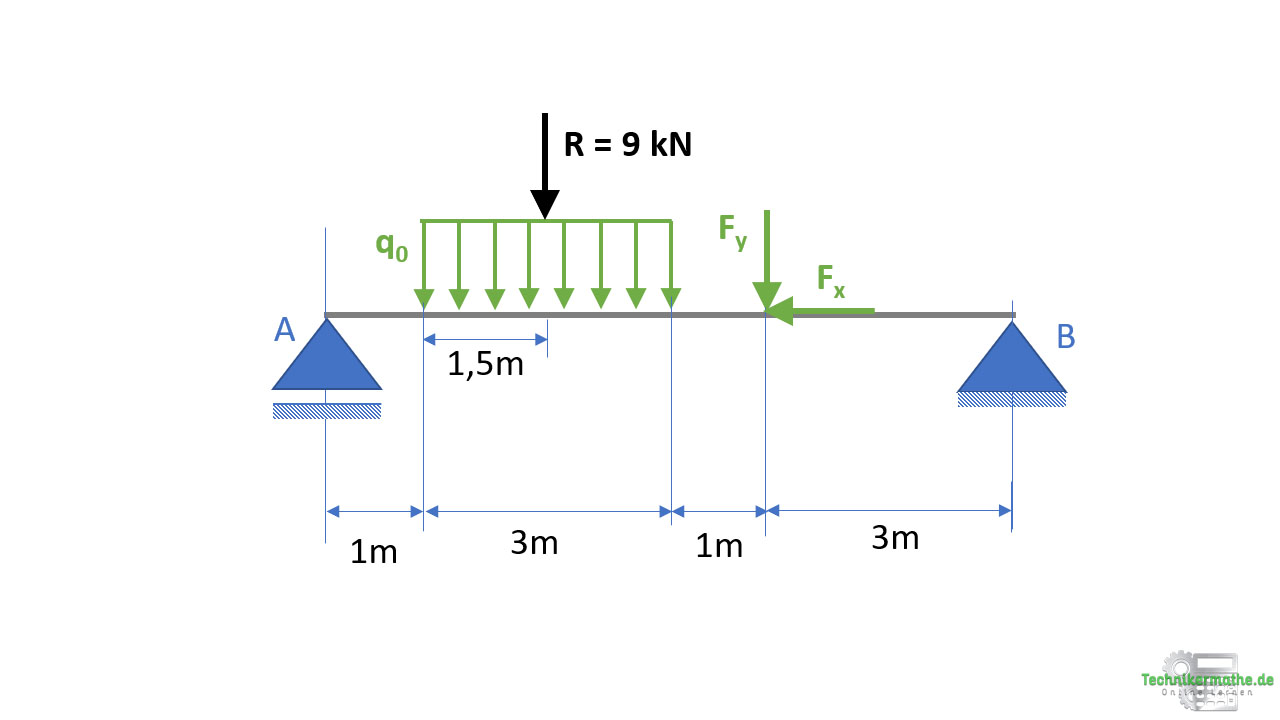
Auflagerkräfte bestimmen

In nächsten Schritt können wir damit beginnen die Auflagerkräfte zu berechnen. Dazu müssen wir den Balken zunächst von seinen Auflagern freischneiden und die Kräfte abtragen:

Schnittgrößen bei rechteckiger Streckenlast, Prüfungsvorbereitung Techniker — Schnittgrößen bei konstanter Streckenlast: Auflagerkräfte bestimmen

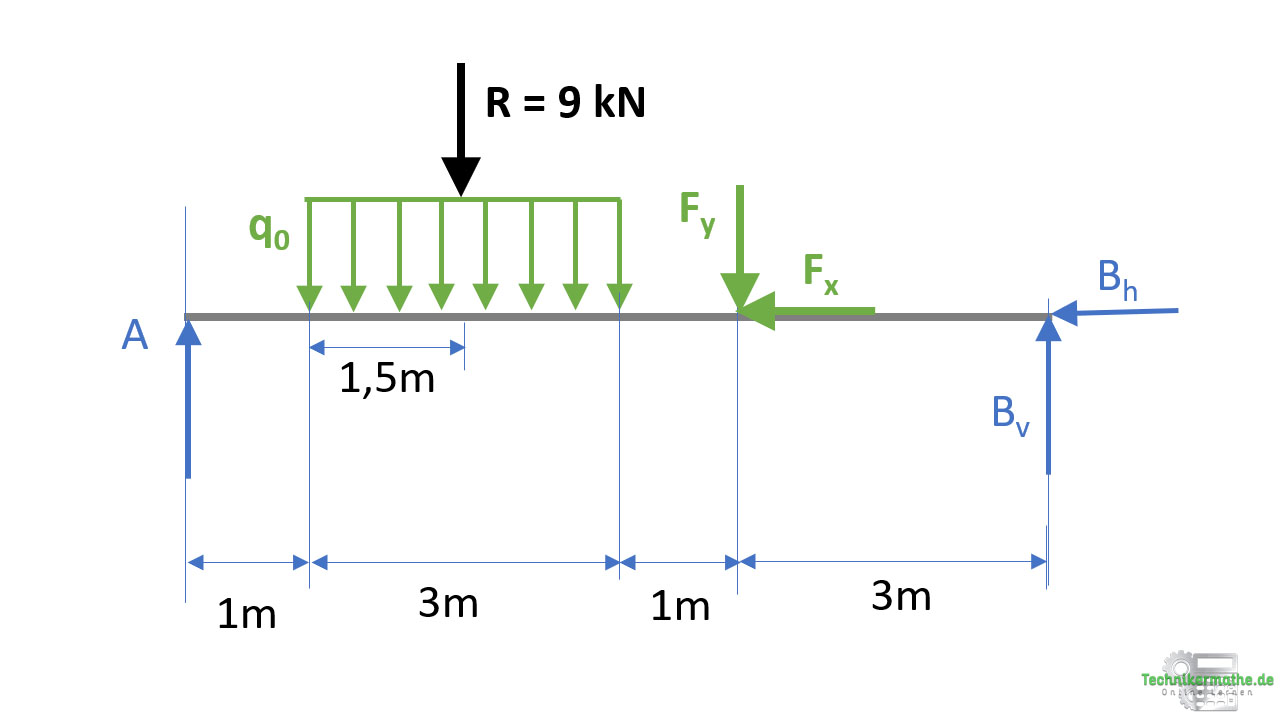
Wir wenden die drei Gleichgewichtsbedingungen der Ebene an, um die Auflagerkräfte zu berechnen.

Gleichgewichtsbedingung in x-Richtung

$-F_x - B_h = 0$

$B_h = -F_x$

$B_h = -3,28 kN$

Gleichgewichtsbedingung in y-Richtung

$A - R - F_y + B_v = 0$

Aus dieser Gleichgewichtsbedingung können wir noch keine Auflagerkraft berechnen, da hier zwei Unbekannte (A und B_v) gegeben sind.

Momentengleichgewichtsbedingung

Wir ziehen also zunächst die Momentengleichgewichtsbedingung heran und legen den Bezugspunkt in das Lager A (alternativ in das Lager B):

$-R \cdot 2,5m - F_y \cdot 5m + B_v \cdot 8m = 0$

$B_v = \dfrac{R \cdot 2,5 m + F_y \cdot 5m}{8m}$

$B_v = \dfrac{9 kN \cdot 2,5 m + 2,29 kN \cdot 5m}{8m}$

$B_v = 4,24 kN$

Aus der vertikalen Gleichgewichtsbedingung können wir jetzt die Auflagerkraft A berechnen:

$A - R - F_y + B_v = 0$

$A = R + F_y - B_v$

$A = 9 kN + 2,29 kN - 4,24 kN$

$A = 7,05 kN$

Wir haben nun alle Auflagerkräfte berechnet und können damit beginnen die Schnittgrößen zu bestimmen.

Schnittgrößen berechnen

Wir müssen wie folgt Schnitte durch den Balken durchführen:

Schnittgrößen, rechteckige Streckenlast, Streckenlast, Schnittbereiche — Schnittgrößen bei konstanter Streckenlast: Schnitte angeben

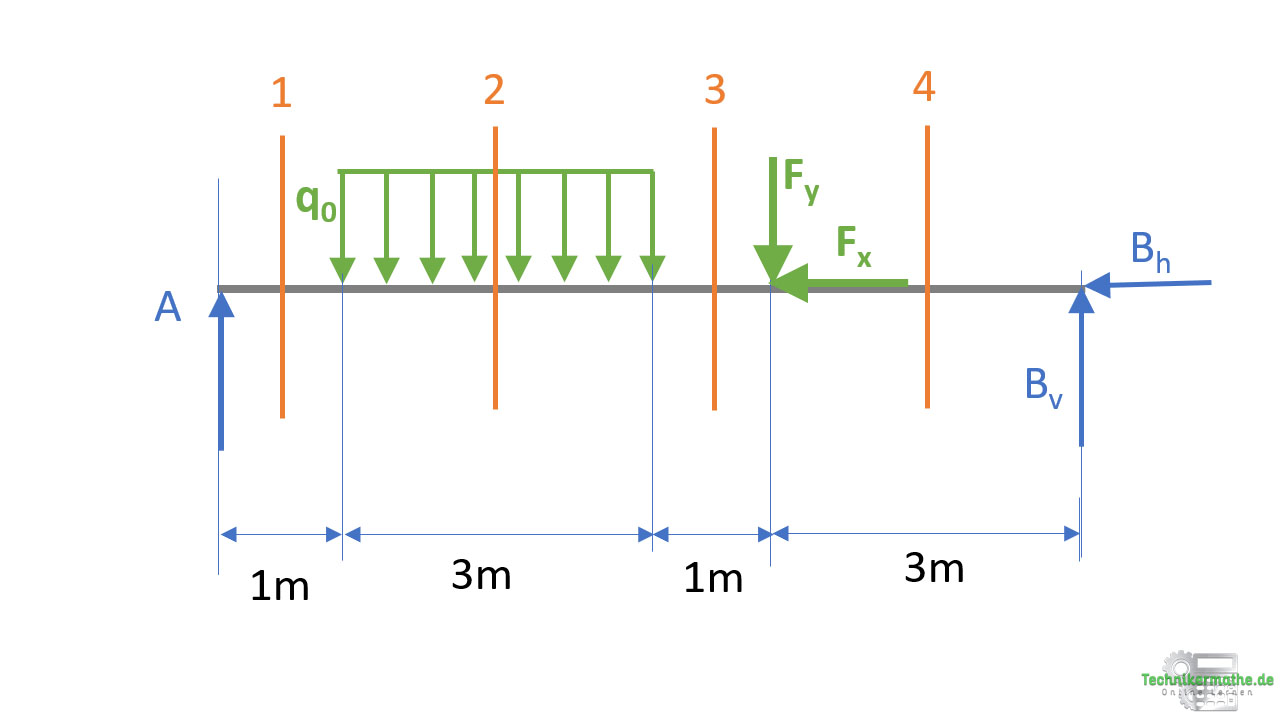
Es wird immer vor bzw. nach einer äußeren Einzelkraft geschnitten. Hierzu zählen auch die Auflagerkräfte. Außerdem wird ein Schnitt durch die Streckenlast vorgenommen. Insgesamt ergeben sich für unser Beispiel vier Schnitte.

Wir können zur Berechnung der Schnittgrößen entweder das linke oder das rechte Schnittufer heranziehen. Beides führt zum selben Ergebnis. Wir starten mit dem 1. Schnitt und wählen das linke Schnittufer.

Schnitt 1: (0 ≤ x ≤ 1m)

Schnittgrößen, Streckenlast, linkes Schnittufer, Schnittufer, Querkraft, Normalkraft, Moment — Schnittgrößen bei konstanter Streckenlast: Schnitt 1

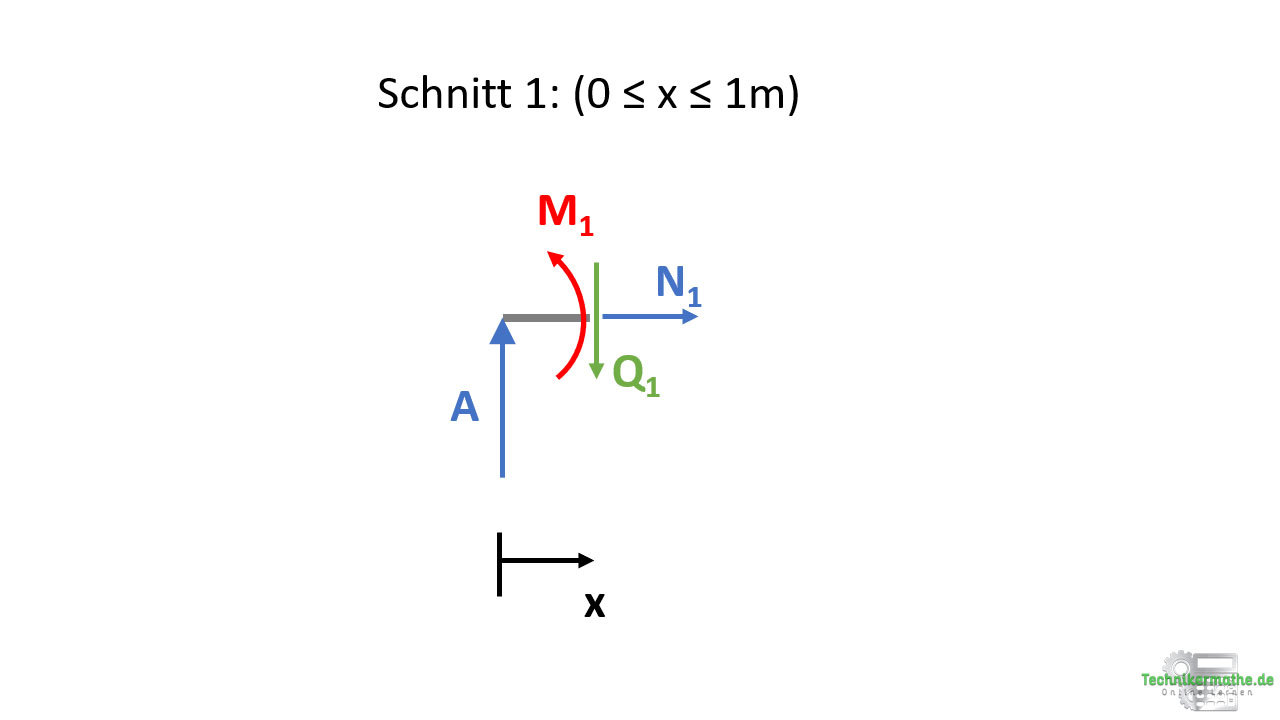
Zur Berechnung der Schnittgrößen wenden wir die Gleichgewichtsbedingungen der Ebene an.

Gleichgewichtsbedingung in x-Richtung

$N_1 = 0$

Gleichgewichtsbedingung in y-Richtung

$A - Q_1 = 0$

$Q_1 = A = 7,05 kN$

Momentengleichgewichtsbedingung

$-A \cdot x + M_1 = 0$

$M_1 = A \cdot x$

$M_1 = 7,05 kN \cdot x$

Als nächstes betrachten wir den 2. Schnitt durch die rechteckige Streckenlast.

Schnitt 2: (1m ≤ x ≤ 4m)

Schnittgrößen, Streckenlast, Resultierende, Schnittufer — Schnittgrößen bei konstanter Streckenlast: Schnitt 2

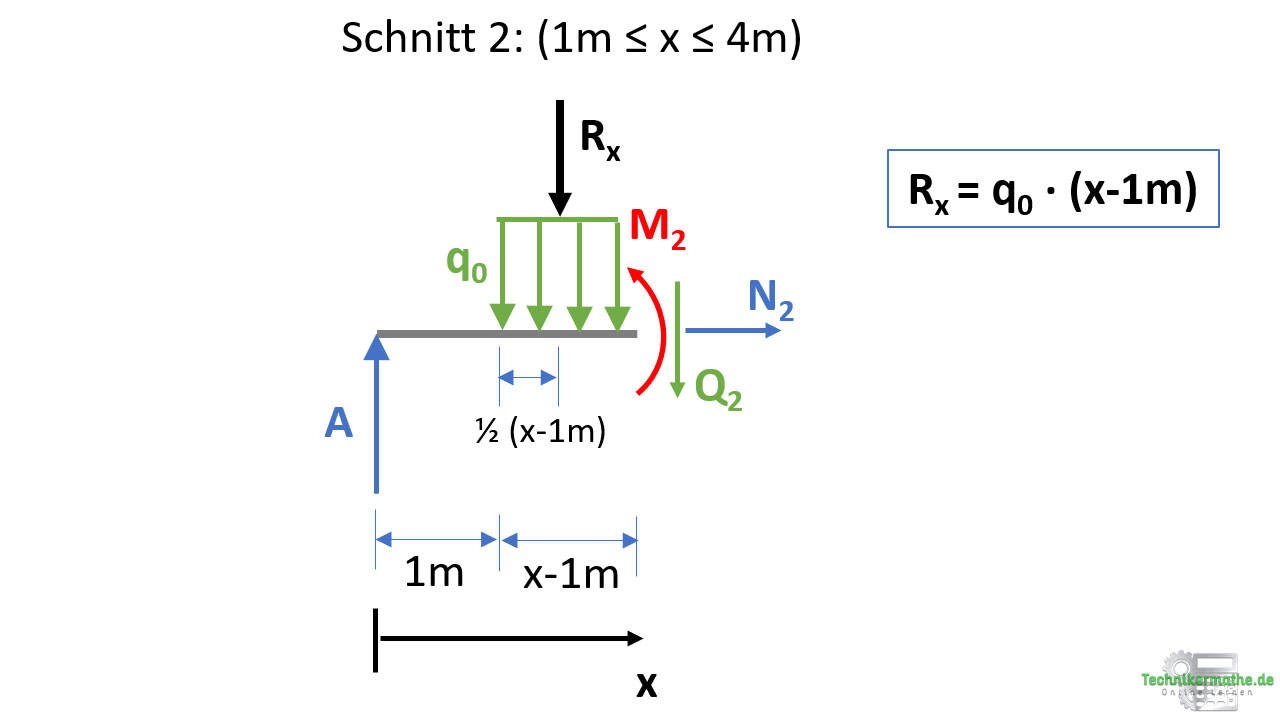
Wir betrachten wieder das linke Schnittufer und schneiden irgendwo zwischen der Streckenlast. Wir haben dann nicht mehr die gesamte Streckenlast gegeben, sondern nur noch eine Teilstreckenlast. Diese weist die Länge x-1m auf. Ihre Länge hängt also davon ab, wo genau der Schnitt durchgeführt wird.

Wir müssen diese Teilstreckenlast zu einer Resultierenden R_x zusammenfassen. Hier gilt es wieder den Flächeninhalt der Teilstreckenlast zu bestimmen (Höhe mal Länge):

$R_x = q_0 \cdot (x-1m)$

$R_x = 3 \frac{kN}{m} \cdot (x-1m)$

Der Angriffspunkt der Resultierenden Rx liegt im Schwerpunkt der Teilstreckenlast, also genau in der Mitte bei der Hälfte der Länge:

$\frac{1}{2} (x-1m)$ Angriffspunkt der Resultierenden

Wir können als nächstes damit beginnen die Schnittgrößen aus den Gleichgewichtsbedingungen zu berechnen.

Gleichgewichtsbedingung in x-Richtung

$N_2 = 0$

Gleichgewichtsbedingung in y-Richtung

$A - R_x - Q_2 = 0$

$Q_2 = A - R_x$

$Q_2 = 7,05 kN - 3 kN \cdot (x-1m)$

Momentengleichgewichtsbedingung

$-A \cdot x + R_x \cdot \frac{1}{2} (x-1m) + M_2 = 0$

$M_2 = A \cdot x - R_x \frac{1}{2} (x-1m)$

$M_2 = 7,05 kN \cdot x - 3 kN \cdot (x-1m) \cdot \frac{1}{2} (x-1m)$

$M_2 = 7,05 kN \cdot x - 1,5 kN \cdot (x-1m)^2$

$M_2 = - 1,5 kN \cdot (x-1m)^2 + 7,05 kN \cdot x$

Die konstante Streckenlast führt zu einem linearen Querkraftverlauf und zu einem quadratischen (=parabelförmigen) Momentenverlauf.

Schnitt 3: (4m ≤ x ≤ 5m)

Für den dritten Schnitt betrachten wir wieder das linke Schnittufer:

Streckenlast, Schnittbereich, Schnittufer, Streckenlast — Schnittgrößen bei konstanter Streckenlast: Schnitt 3

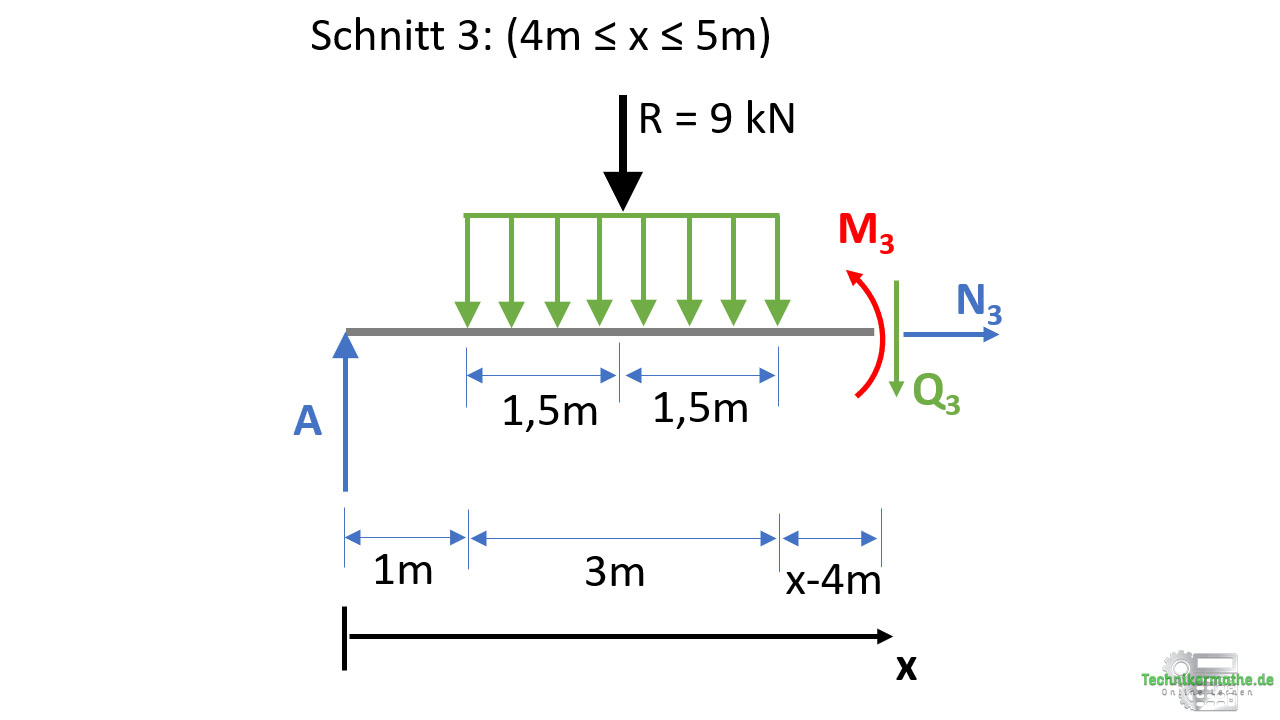
Wenn wir das linke Schnittufer betrachten, dann müssen wir für den 3. Schnitt (und auch für den 4. Schnitt) die gesamte Streckenlast betrachten, weil diese vor dem 3. Schnittbereich liegt. Hier wird dann wieder die Resultierende der gesamten Streckenlast gebildet, so wie bereits bei den Auflagerkräften gezeigt.

Gleichgewichtsbedingung in x-Richtung

$N_3 = 0$

Gleichgewichtsbedingung in y-Richtung

$A - R - Q_3 = 0$

$Q_3 = A - R$

$Q_3 = 7,05 kN - 9 kN$

$Q_3 = -1,95 kN$

Momentengleichgewichtsbedingung

$-A \cdot x + R \cdot (1,5 m + x -4m) + M_3 = 0$

$M_3 = A \cdot x - R (x - 2,5m)$

$M_3 = 7,05 kN \cdot x - 9kN \cdot (x-2,5m)$

$M_3 = 7,05 kN \cdot x - 9kN \cdot x + 22,5 kNm$

$M_3 = -1,95 kN \cdot x + 22,5 kNm$

Schnitt 4: (5m ≤ x ≤ 8m)

Für letzten Schnitt betrachten wir das rechte Schnittufer:

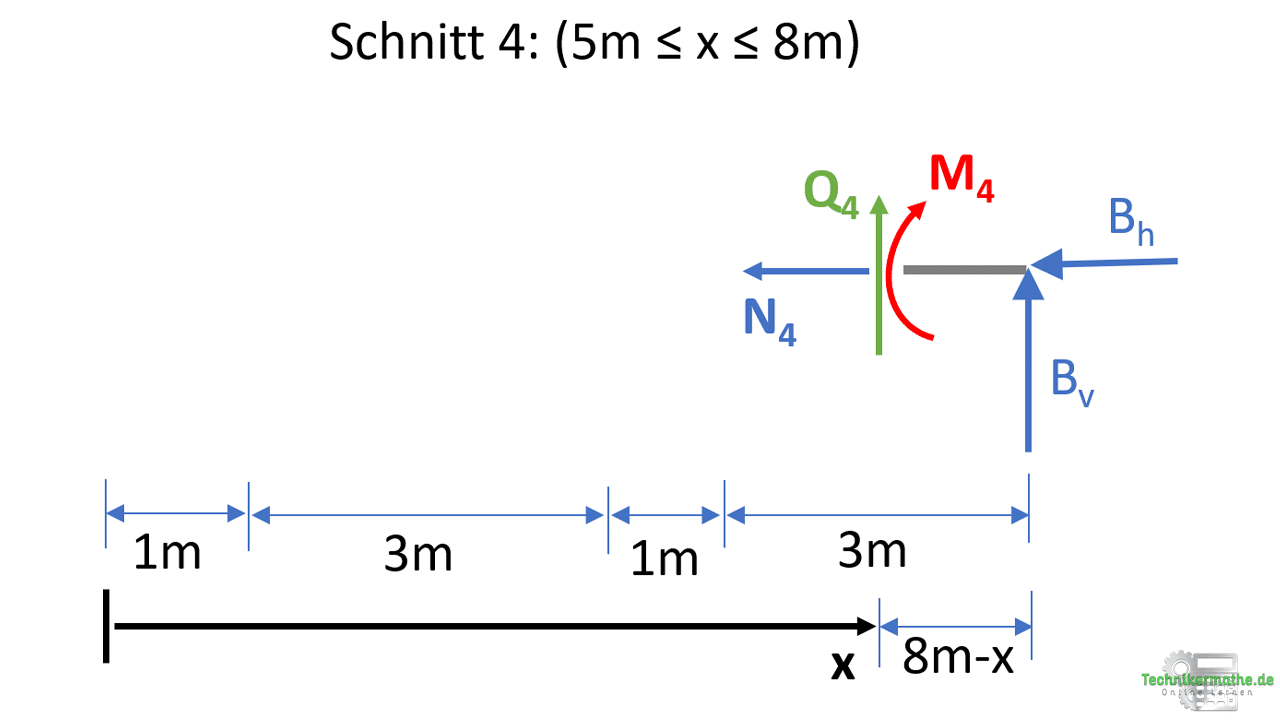
Schnittgrößen, rechtes Schnittufer, Streckenlast, Beispiel — Schnittgrößen bei konstanter Streckenlast: Schnitt 3

Wir können nun wieder die Schnittgrößen aus den Gleichgewichtsbedingungen berechnen.

Gleichgewichtsbedingung in x-Richtung

$-N_4 - B_h = 0$

$N_4 = -B_h = -(-3,28 kN)$

$N_4 = 3,28 kN$

Gleichgewichtsbedingung in y-Richtung

$B_v + Q_4 = 0$

$Q_4 = -B_v$

$Q_4 = -4,24 kN$

Momentengleichgewichtsbedingung

$B_v \cdot (8m-x) - M_4 = 0$

$M_4 = B_v \cdot (8m-x)$

$M_4 = 4,24 kN \cdot (8m-x)$

$M_4 = -4,24 kN \cdot x +33,92 kN$

Wir haben alle Schnittgrößen berechnet. Wir können als nächstes die Schnittgrößenverläufe einzeichnen.

Schnittgrößenverläufe

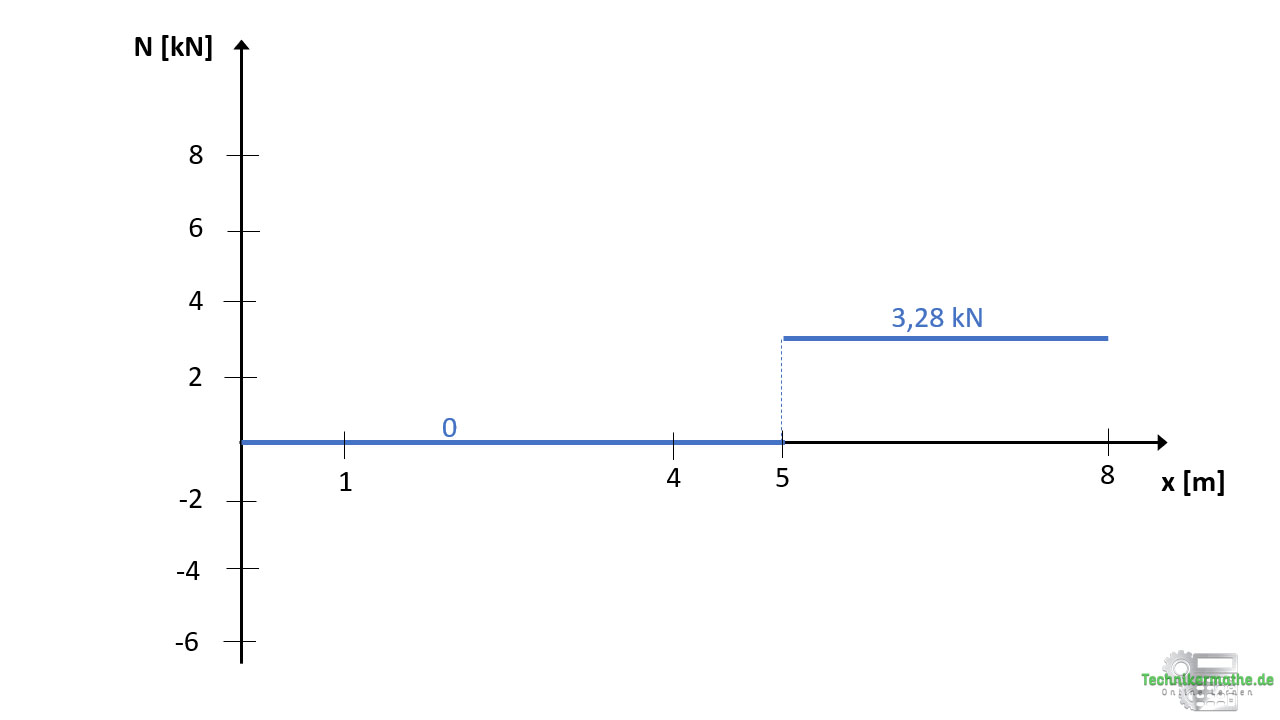
Normalkraftverlauf

Beginnen wir mit der Normalkraft, die in den ersten drei Schnittbereichen Null ist, weil dort keine horizontale Kraft angreift. Im vierten Schnittbereich ist diese konstant bei 3,28 kN infolge der äußeren Kraft F_x:

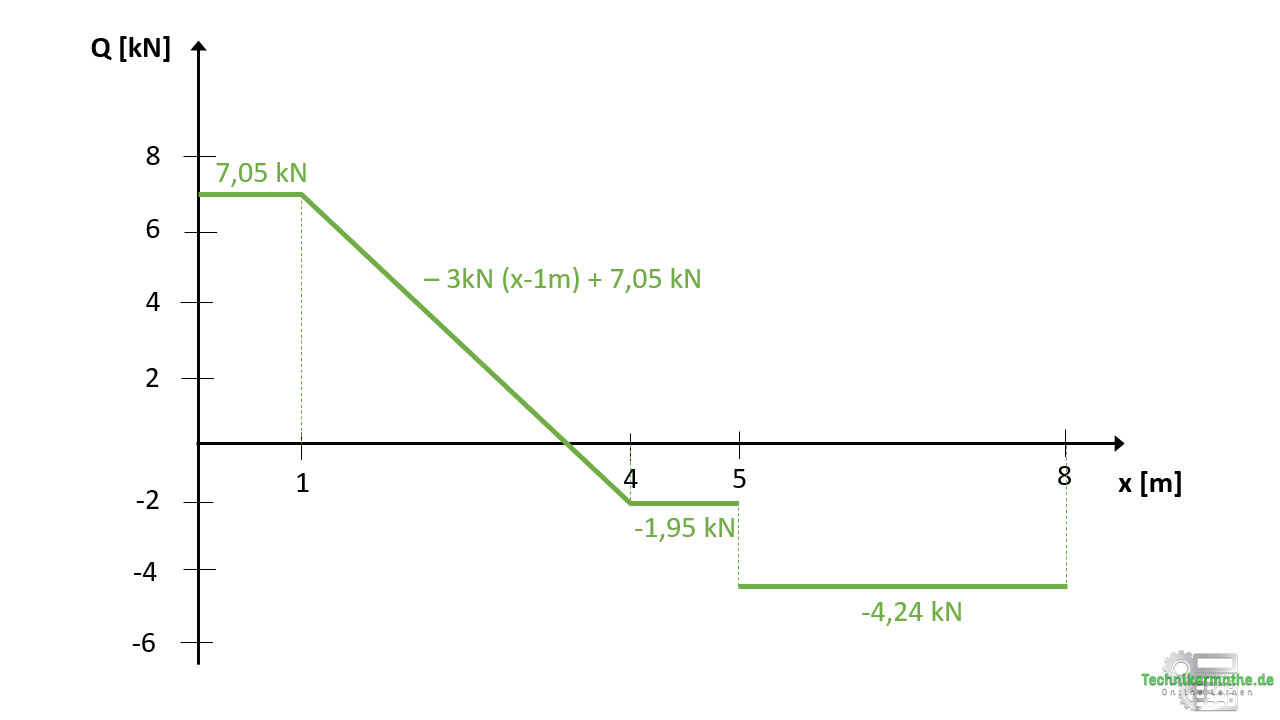
Querkraftverlauf

Die Querkraft ist zunächst konstant bei 7,05 kN infolge der angreifenden Lagerkraft A. Danach ergibt sich ein linearer Querkraftverlauf mit negativer Steigung infolge der im 2. Schnittbereich angreifenden rechteckigen Streckenlast. Im 3. Schnittbereich ist die Querkraft konstant bei -1,95 kN und im 4. Schnittbereich ist die Querkraft konstant bei -4,24 kN.

Du solltest dir folgendes für den Querkraftverlauf merken:

Merk’s dir!

Die Querkraft ist in lastfreien Bereichen konstant, d.h. der Wert der Querkraft ändert sich nicht.
An der Stelle, an der eine äußere Einzellast angreift, weist der Querkraftverlauf einen Sprung in der Größe der angreifenden äußeren vertikalen Einzellast auf.
In Bereichen mit konstanter (rechteckiger) Streckenlast verläuft der Querkraftverlauf linear.

Die Querkraft weist im 2. Schnittbereich einen Nulldurchgang auf. Der wird später relevant, weil hier für den Momentenverlauf ein Maximum oder Minimum gegeben ist. Du kannst aus dem Querkraftverlauf die Stelle berechnen, an welcher die Querkraft einen Nulldurchgang aufweist, indem du die dort geltende Funktion gleich Null setzt und nach x auflöst:

$Q_2 = 7,05 kN - 3 kN \cdot (x-1m) = 0$ |Einheiten weglassen

$Q_2 = 7,05 - 3 \cdot (x-1) = 0$ |Klammer auflösen

$7,05 - 3 \cdot x + 3 = 0$ |Zusammenfassen

$10,05 - 3x = 0$ | $+3x$

$10,05 = 3x$ | $:3$

$x = 3,35$

An der Stelle x = 3,35 weist die Querkraft einen Nulldurchgang auf, hier ist sie also gleich Null. An dieser Stelle weist der Momentenverlauf einen Extremwert auf.

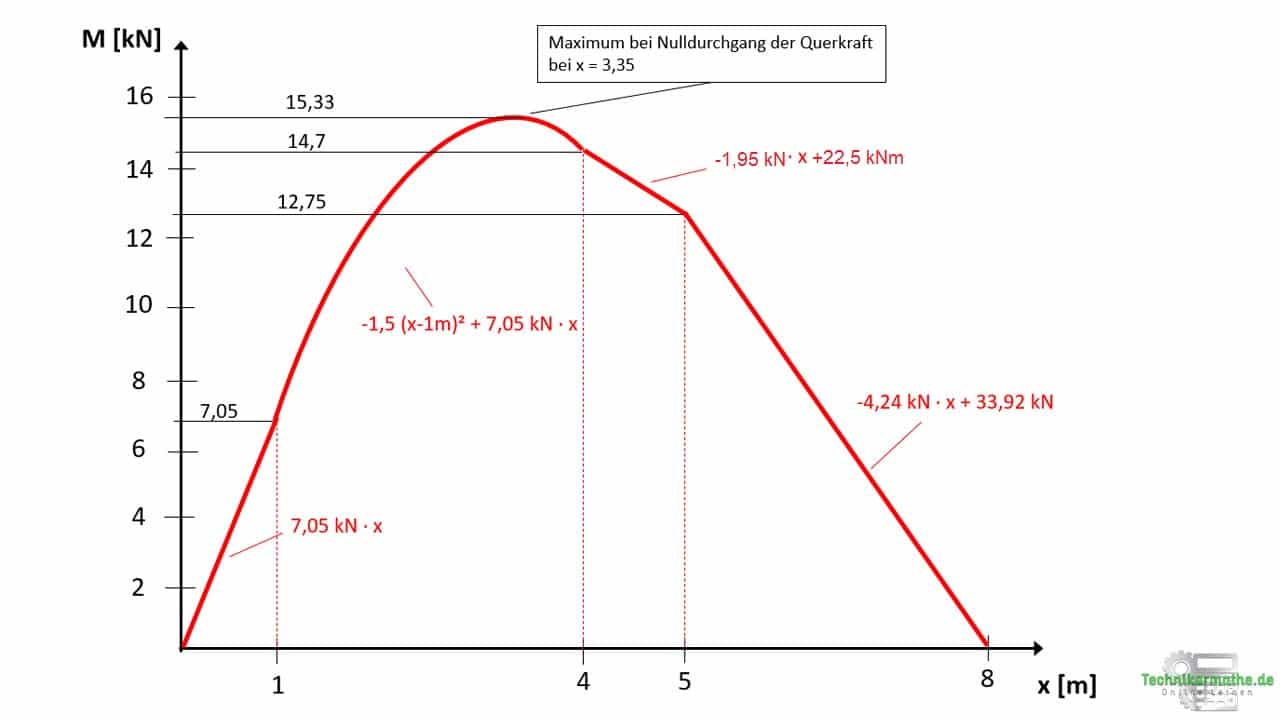
Momentenverlauf

Das Moment ist in allen Schnittbereichen eine lineare Funktion, bis auf den Schnittbereich, wo die rechteckige Streckenlast gegeben ist. Hier liegt ein parabelförmiger Verlauf der Streckenlast vor. Dabei handelt es sich um eine nach unten geöffnete Parabel. An den Lagern A (x = 0) und B (x = 8m) ist das Moment Null, weil Loslager und Festlager keine Momente übertragen.

Du solltest dir folgendes für den Momentenverlauf merken:

Merk’s dir!

Der Momentenverlauf ist in lastfreien Bereichen linear. In Sonderfällen ist die Momentenlinie dort Null.
An der Stelle, an der eine äußere Einzellast angreift, hat der Momentenverlauf einen Knick.
In Bereichen mit konstanter Streckenlast ist der Momentenverlauf quadratisch (parabelförmig).
Der Momentenverlauf hat einen Extremwert an der Stelle, wo der Querkraftverlauf einen Nulldurchgang hat.

In der obigen Grafik sieht du für den 2. Schnittbereich (zwischen 1m und 4m) einen parabelförmigen Verlauf gegeben. Du kannst vorher schlecht abschätzen, ob der quadratische Momentenverlauf ein Extremwert (Maximum oder Minimum) aufweist.

Deswegen schauen wir uns den Querkraftverlauf an. Dieser weist einen Nulldurchgang auf. An dieser Stelle ist die Querkraft gleich Null. Für den Momentenverlauf gilt an dieser Stelle, dass diese einen Extremwert (Maximum oder Minimum) aufweist.

Wir kennen die Stelle, an welcher der Momentenverlauf einen Extremwert aufweist. Diese haben wir bereits aus dem Nulldurchgang des Querkraftverlaufs bestimmt (x = 3,35). Wir können diese Stelle aber auch aus dem Momentenverlauf ermitteln.

Dazu können wir einfach den Momentenverlauf des 2. Schnittbereichs heranziehen und die Extremwerte berechnen.

Wiederholung Extremwerte berechnen – Vorgehensweise

1.Ableitung bilden, gleich Null setzen und nach x auflösen. An dieser Stelle ist ein Maximum oder Minimum gegeben.

2. Ableitung bilden:
-> Größer Null = Minimum
-> Kleiner Null = Maximum

Bei Funktionen x³ und höher musst du in die 2. Ableitung noch zusätzlich den ermittelten x-Wert einsetzen, um zu bestimmen, ob ein Maximum oder Minimum gegeben ist.

Wir schauen uns den Momentenverlauf an:

$M_2 = - 1,5 kN \cdot (x-1m)^2 + 7,05 kN \cdot x$

Wir berechnen das Ganze ohne Einheiten:

$M_2 = - 1,5 \cdot (x-1)^2 + 7,05 \cdot x$

Wir bilden die 1. Ableitung und setzen diese gleich Null (denk an innere mal äußere Ableitung der Klammer):

$M_2' = -3 (x-1) + 7,05 = 0$

Wir lösen die 1. Ableitung nach x auf:

$M_2' = -3 (x-1) + 7,05 = 0$

$-3 \cdot x + 3 + 7,05 = 0$

$-3 \cdot x + 10,05 = 0$ | $-10,05$

$-3 \cdot x = -10,05$ | $:(-3)$

$x = 3,35$

Wir bilden die 2. Ableitung:

$M_2' = -3 kN$ (Maximum)

Wir haben an der Stelle x = 3,35 ein Maximum gegeben.

Was kommt als Nächstes?

Nachdem wir die Schnittgrößen bei konstanter Streckenlast betrachtet haben, wollen wir uns in der folgenden Lerneinheit anschauen, wie du die Schnittgrößen bei einer dreieckigen Streckenlast bestimmst und wie die Schnittgrößenverläufe gezeichnet werden.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++