TM1 – Resultierende im allgemeinen Kräftesystem

Die Resultierende oder resultierende Kraft ist die Zusammenfassung mehrerer Einzelkräfte zu einer einzigen Kraft. Dabei müssen wir zwischen dem zentralen und allgemeinen Kräftesystem unterscheiden. Im allgemeinen Kräftesystem müssen wir den Betrag, die Richtung und die Lage der Resultierenden aus den gegebenen Einzelkräften bestimmen.

Für ein optimales Verständnis helfen dir fünf ausführliche Videoclips und ein anschauliches Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Statik findest du im Onlinekurs: TM1 – Statik.

In dieser Lerneinheit zeigen wir dir, wie du die Resultierende bestimmen kannst. Dabei betrachten wir Kräfte in einem allgemeinen Kräftesystem.

Wir zeigen dir ganz ausführlich wie du Kräfte zu einer einzigen Kraft, der sogenannten Resultierenden, zusammenfassen kannst. Dabei betrachten wir das allgemeine Kräftesystem, in welchem sich die gegebenen Kräfte nicht alle in einem einzigen Punkt schneiden.

Die Resultierende ist die Zusammenfassung von Einzelkräfte zu einer einzigen Kraft. Diese Kraft weist genau dieselbe Wirkung auf den Körper auf, wie die Einzelkräfte zusammen.

Schauen wir uns mal an, wie wir vorgehen müssen und welche Gleichungen wir benötigen, wenn wir die Resultierende bestimmen sollen. Danach folgt ein ausführliches Beispiel zur Berechnung der Resultierenden.

Videoreihe: Resultierende im allgemeinen Kräftesystem

In dieser Videoreihe zeigen wir dir ausführlich, wie du den Betrag, die Richtung und die Lage der Resultierende im allgemeinen Kräftesystem bestimmst:

Lernclips

Resultierende bestimmen

1.Aufgabenstellung und Kräftezerlegung

2. Teilresultierende bestimmen

3. Betrag und Richtung der Resultierenden bestimmen

4. Lage der Resultierenden bestimmen

5. Resultierende einzeichnen

Vorgehensweise: Resultierende bestimmen (allgemeines Kräftesystem)

Wenn wir für Kräfte in einem allgemeinen Kräftesystem die Resultierende bestimmen sollen, dann wollen wir den Betrag, die Richtung und die Lage der Resultierenden bestimmen. Dazu kannst du dir die folgenden Schritte merken:

Vorgehensweise: Resultierende bestimmen

1.Durchführung der Kräftezerlegung für alle Kräfte die in der Ebene wirken (alle Kräfte mit Winkel).

2. Ersetzen der Kräfte mit Winkel durch ihre Kraftkomponenten aus 1.

3. Berechnung der Teilresultierenden R_x und R_y.

4. Berechnung des Betrags der Resultierenden aus den Teilresultierenden R_x und R_y.

5. Bestimmung der Richtung der Resultierenden (z.B. Winkel zur Waagerechten) aus den Teilresultierenden R_x und R_y.

6. Berechnung der Summe aller Momente der Einzelkräfte auf einen festgelegten Bezugspunkt.

7. Berechnung der Lage der Resultierenden.

Wenn du die obigen Schritte durchführst, dann erhältst du am Ende den Betrag, die Richtung und die Lage der Resultierenden. Schauen wir uns mal die Gleichungen an, die du benötigst, um die Resultierenden bestimmen zu können.

Gleichungen: Resultierende bestimmen

Kräftezerlegung

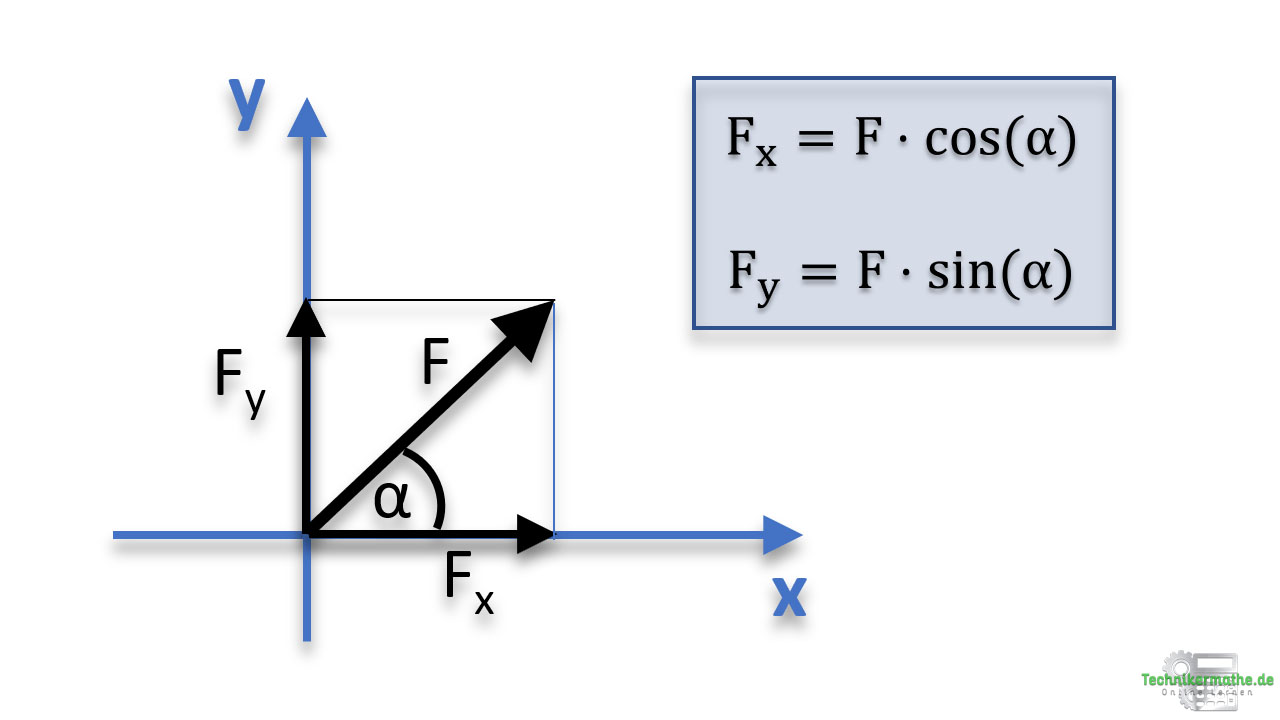
Die Kräftezerlegung musst du dann durchführen, wenn Kräfte in der Ebene wirken. Diese Kräfte weisen einen Kraftanteil in x- und in y-Richtung auf. Für die Berechnung der Teilresultierenden müssen wir diese Kraftanteile kennen. So geht der Kraftanteil in x-Richtung in die Bestimmung der Teilresultierenden R_x ein und der Kraftanteil in y-Richtung in die Bestimmung der Resultierenden R_y:

Kräftezerlegung

$F_x = F \cdot cos(\alpha)$

$F_y = F \cdot sin(\alpha)$

Damit die Gleichungen gelten, muss der Winkel zur Horizontalen (zur x-Achse) gegeben sein. Hierbei ist F die Kraft die zerlegt werden soll und α der Winkel zur Horizontalen.

Berechnung der Teilresultierenden R_x und R_y

Wir können im nächsten Schritt die Teilresultierenden R_x und R_y berechnen. R_x ist die Zusammenfassung aller Kräfte die in x-Richtung wirken, R_y die Zusammenfassung aller Kräfte die in y-Richtung wirken.

$R_x = \sum F_{ix}$ Summe aller Kräfte in x-Richtung

$R_y = \sum F_{iy}$ Summe aller Kräfte in y-Richtung

Bei der späteren Berechnung der Teilresultierenden R_x und R_y ist es wichtig, dass du auf die Vorzeichen achtest. So werden Kräfte die in positive Achsenrichtung wirken addiert und Kräfte die negative Achsenrichtung wirken subtrahiert.

Betrag der Resultierenden

Die beiden Teilresultierenden liegen auf den Achsen und sind damit rechtwinklig zueinander. Zwei rechtwinklige Kräfte können zu einer Kraft mittels Satz des Pyhtagoras zusammengefasst werden. Um den Betrag der Resultierenden bestimmen zu können, kannst du also Satz des Pythagoras anwenden:

Betrag der Resultierenden

$R = \sqrt{R_x^2 + R_y^2}$

Richtung der Resultierenden

Die Richtung der Resultierenden wird bestimmt, indem der Winkel zur Horizontalen oder zur Vertikalen angegeben wird. Wenn wir den Winkel aus den beiden Teilresultierenden bestimmen, dann können wir den Tanges anwenden:

Winkel von der Horizontalen zur Resultierenden

$\tan(\alpha) = \dfrac{R_y}{R_x}$

Hierbei handelt es sich um den Winkel von Rx zu R, damit also um den Winkel von der Horizontalen zur Resultierenden.

Hierbei handelt es sich um den Winkel von R_x zu R. Mit der obigen Gleichung wird also der Winkel von der Horizontalen zur Resultierenden berechnet. Sollst du den Winkel zur Senkrechten angeben, so musst du einfach 90° – α rechnen.

Bestimmung des resultierenden Moments

Wir müssen das resultierende Moment M_R ermitteln, um im letzten Schritt die Lage der Resultierenden bestimmen zu können. Das resultierende Moment M_R ist nichts anderes als die Summe aller Moment der Einzelkräfte auf einen festgelegten Bezugspunkt X:

Resultierendes Moment

$M_R^X = \sum M_i^X$

Das resultierende Moment ist demnach auch das Moment, welches die Resultierende R auf den Bezugspunkt X ausübt.

Bestimmung der Lage der Resultierenden (=resultierendes Moment)

Betrachten wir die Resultierende, dann übt diese ein Moment auf einen bestimmten Bezugspunkt aus. Dieses Moment kann auch mit der folgenden Gleichung berechnet werden:

Resultierendes Moment

$M_R^X = R \cdot h$

Hierbei ist M_R das Moment welches die Resultierende ausübt, X der festgelegte Bezugspunkt auf welchen das Moment ausgeübt wird, R die Resultierende und h der Hebelarm, also der senkrechte Abstand von der Resultierenden zum Bezugspunkt X.

Wir suchen hier die Lage der Resultierenden. Diese können wir mittels Hebelarm angeben. Wir stellen also die obige Gleichung nach h um:

Lage der Resultierenden

$h = \dfrac{M_R}{R}$

Wir geben damit die Lage der Resultierenden h mit dem senkrechten Abstand vom gewählten Bezugspunkt X zur Resultierenden an.

Beispiel: Resultierende berechnen

Aufgabenstellung

Resultierende bestimmen, Beispiel, Balken, Berechnung, Lösung — Resultierende bestimmen

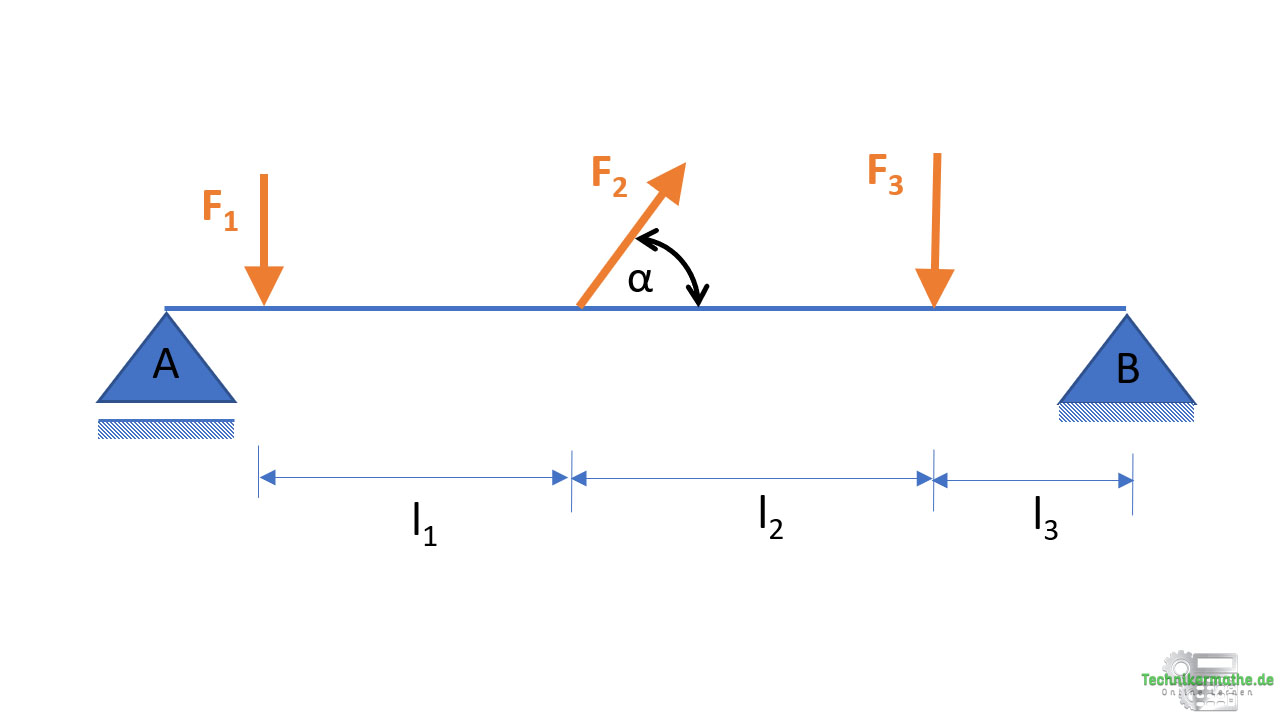
Gegeben sei eine Hubbrücke für Fußgänger, die einen kleinen Kanal überspannt. Die Brücke wird durch ein Seil mit einer Zugkraft von F_s = 60 kN gehalten. Die Zugkraft greift in einem Winkel von α=58° an. Außerdem wirken zwei parallele Kräfte F₁ = 80 kN und F₂ = 40 kN auf die Hubbrücke. Die Kräfte weisen die folgenden Abständen zueinander auf:

l₁=4m, l₂=2m und l₃=1m

Bestimme
a) den Betrag der Resultierenden R,
b) den Winkel α_R der Resultierenden (zur Vertikalen) sowie
c) den senkrechten Abstand (=Hebelarm) der Resultierenden zum Lager B.

a) Betrag der Resultierenden R

Bevor wir mit der Berechnung des Betrags der Resultierenden beginnen können, müssen wir zunächst Kräfte mit einem Winkel in ihre Komponenten zerlegen. Im obigen Beispiel müssen wir zunächst die Seilkraft FS in ihre x- und y-Komponente zerlegen:

Beispiel, Resultierende im allgemeinen Kräftesystem, Kräftezerlegung — Resultierende bestimmen

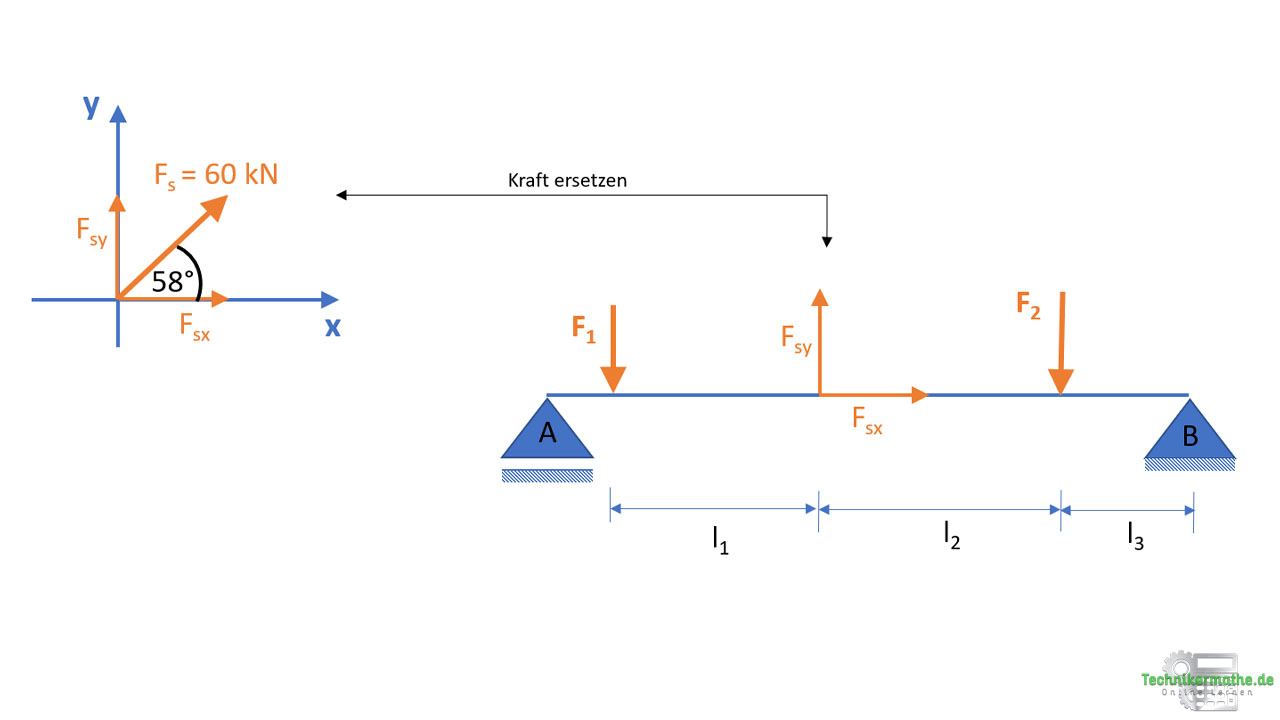
Die Berechnung der Kraftanteile erfolgt zu:

$F_{sx} = F_s \cdot \cos(\alpha) = 60 kN \cdot \cos(58^\circ) = 31,8 N$

$F_{sy} = F_s \cdot \sin(\alpha) = 60 kN \cdot \sin(58^\circ) = 50,9 N$

Wir können als nächstes die Teilresultierenden R_x und R_y bestimmen.

Teilresultierende R_x

$R_x = \sum F_{ix} = + F_{sx}$

$R_x = +31,8 kN$

Wir haben hier nur eine Kraft in x-Richtung gegeben und zwar den Kraftanteil F_sx der Kraft F_s. Diese Kraft zeigt in positive x-Richtung, damit ist die Teilresultierende R_x positiv und zeigt damit in positive x-Richtung.

Teilresultierende R_y

$R_y = \sum F_{iy} = -F_1 + F_{sy} - F_2$

$R_y = -80 kN + 50,9 kN - 40 kN = -69,1 kN$

Die Kraft F₁ zeigt in negative y-Richtung, wird deswegen negativ berücksichtigt, genau wie die Kraft F₂. Der Kraftanteil F_sy zeigt in positive y-Richtung, wird also positiv berücksichtigt. Die Teilresultierende Ry ist negativ und zeigt damit in negative y-Richtung.

Teilresultierende, Resultierende, Koordinatensystem — Resultierende bestimmen

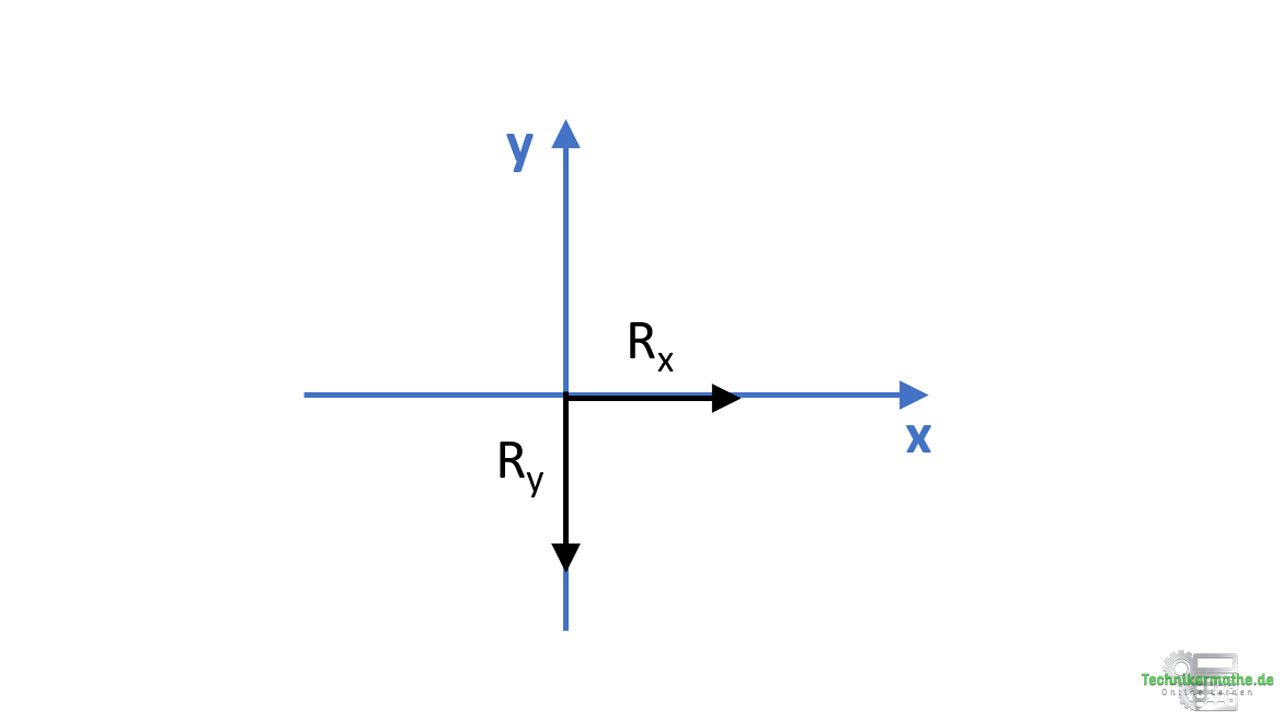
Resultierende bestimmen

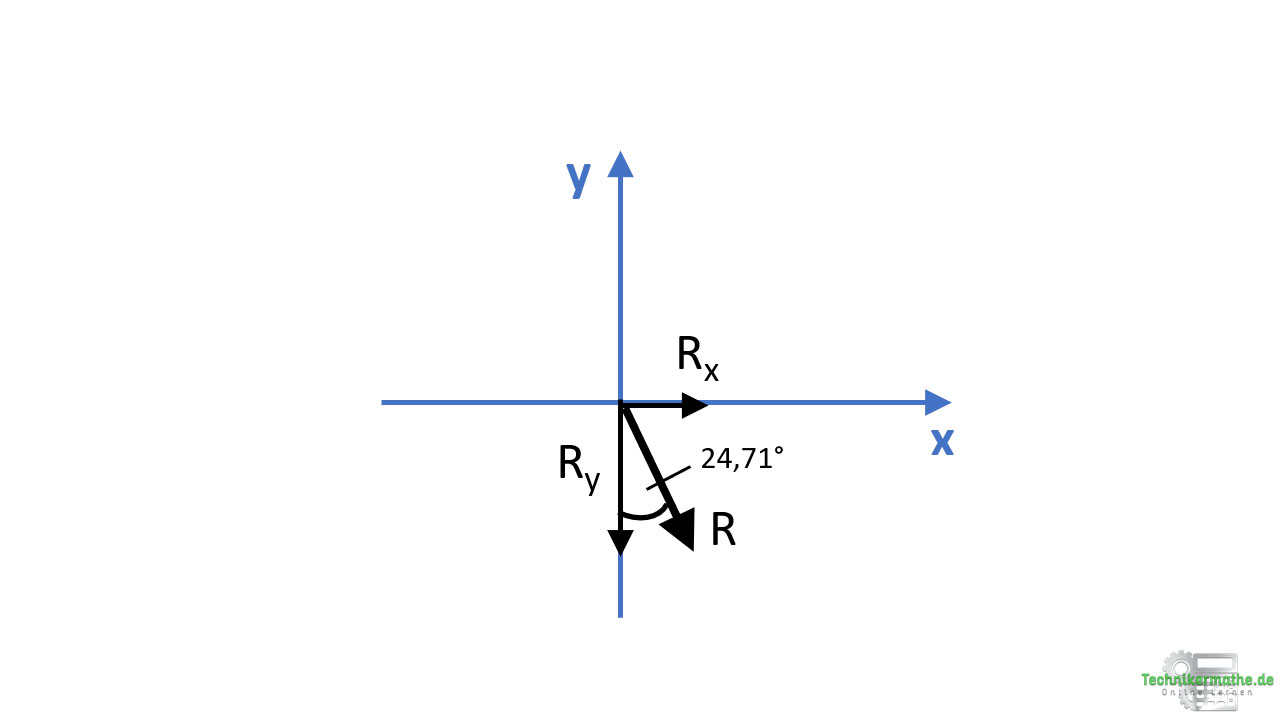
Wir können als nächstes aus den beiden Teilresultierenden die Resultierende bestimmen. Diese liegt irgendwo im 4. Quadranten des obigen Koordinatensystems. Wir können die Richtung der Resultierenden also schon grob abschätzen.

Den Betrag der Resultierenden können wir mittels Satz des Pythagoras berechnen:

$R = \sqrt{R_x^2 + R_y^2} = \sqrt{(31,8 kN)^2 + (-69,1 kN)^2} = 76,1 kN$

Die Resultierende weist einen Betrag von 76,1 kN auf.

a) Winkel zur Vertikalen – Richtung der Resultierenden

In der Lösung b wollen wir die Richtung der Resultierenden bestimmen bzw. den Winkel zur Vertikalen. Wir können den Winkel zur Horizontalen über die beiden Teilresultierenden mittels Tangens berechnen:

$\tan(\alpha_R) = \dfrac{R_y}{R_x}$

Hierbei handelt es sich um den Winkel von der Teilresultierenden R_x zur Resultierenden R. Da R_x auf der x-Achse liegt, handelt sich also um den Winkel von der Horizontalen zur Resultierenden.

Wir lösen die obige Gleichung nach dem Winkel α_R auf:

$\alpha_R = tan^{-1}(\dfrac{R_y}{R_x})$

Einsetzen der Werte:

$\alpha_R = tan^{-1}(\dfrac{-69,1 kN}{31,8 kN}) = -65,29^{\circ}$

Der Winkel von der R_x zur Resultierenden beträgt 65,29°. Das Minuszeichen bedeutet, dass die Winkelabtragung von R_x zu R in einer Rechtsdrehung erfolgen muss (negativer Drehsinn). Das ist aber auch aus der Grafik erkennbar, so dass du das Vorzeichen gar nicht weiter beachten musst. Denn aus der obigen Grafik wissen wir, dass die Resultierende im 4. Quadranten liegen muss und wissen demnach auch, wie der Winkel abzutragen ist.

Wir suchen nun aber den Winkel zur Vertikalen:

$90^{\circ} - 65,29^{\circ} = 27,71^\circ$

Richtung der Resultierenden, Winkel, allgemeines Kräftesystem, Resultierende — Resultierende bestimmen

c) Bestimmung des Hebelarms – Lage der Resultierenden

resultierendes Moment, Hebelarm, Resultierende, allgemeines Kräftesystem, Lage der Resultierenden — Resultierende bestimmen

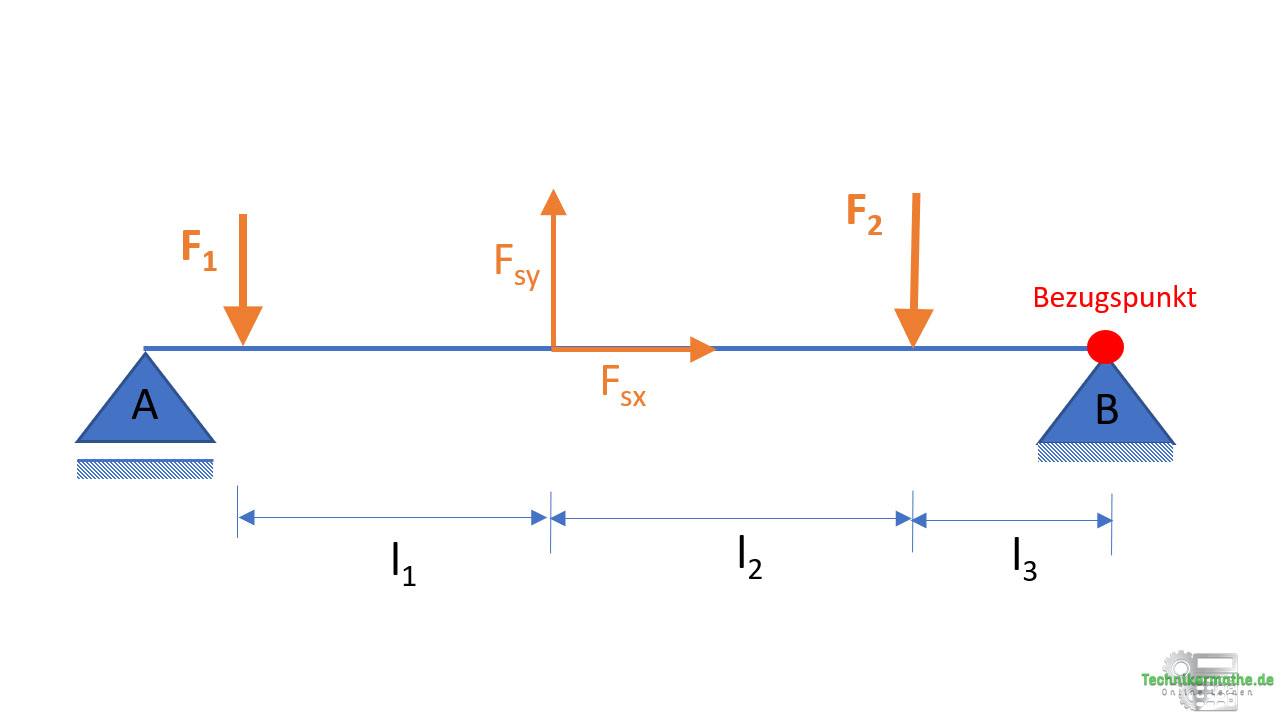
In der letzten Aufgabenstellung wollen wir die Lage der Resultierenden in Bezug auf das Lager B bestimmen. Zunächst müssen wir dazu aber das resultierende Moment aus der Summe der Einzelmomente bestimmen. Da wir den Abstand zum Lager B suchen, legen wir hier unseren Bezugspunkt für die Bestimmung der Moment hin:

$M_R^B = \sum M_i^{B} = F_1 \cdot (l_1 + l_2 + l_3) - F_{sy} \cdot (l_2 + l_3) + F_2 \cdot l_3$

Einsetzen der Werte:

$M_R^B = 80 kN \cdot 7m - 50,9 N \cdot 3m + 40 kN \cdot 1m = 447,3 kNm$

Das resultierende Moment beträgt demnach 447,3 Nm. Um den Abstand vom Bezugspunkt (Lager B) zur Resultierenden bestimmen zu können, können wir den Hebelarm berechnen:

$h = \dfrac{M_R}{R} = \dfrac{447,3 kNm}{76,1 kN} = 5,88 m$

Der senkrechte Abstand vom gewählten Bezugspunkt zur Resultierenden beträgt 5,88m. Da der Bezugspunkt im Lager B liegt, ist dies auch gleichzeitig der senkrechte Abstand vom Lager B zum Bezugspunkt.

Hebelarm, Resultierende einzeichnen, Resultierendes Moment, allgemeines Kräftesystem, senkrechter Abstand — Resultierende bestimmen

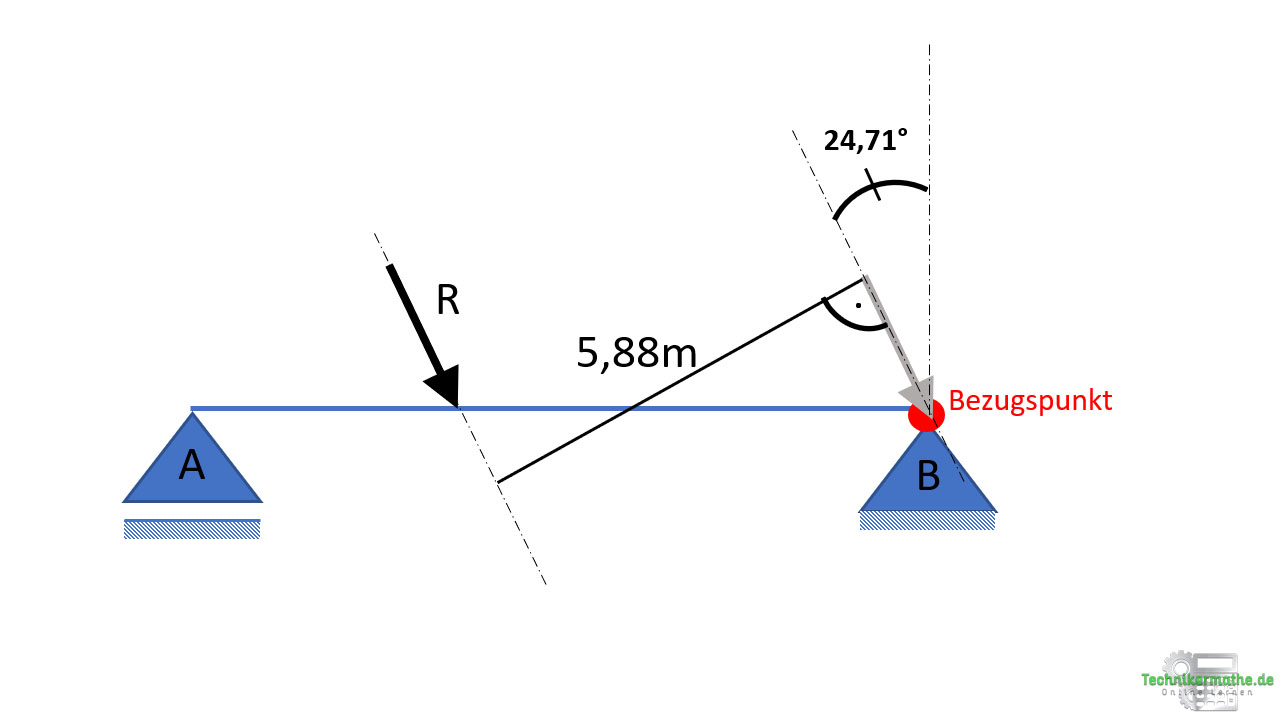
Die Resultierende mit der Größe von 76,1 kN, dem Winkel von 24,71° zur Senkrechten sowie dem senkrechten Abstand von 5,88m vom Lager B ausgehend weist dieselbe Wirkung auf den Balken auf, wie die 3 Einzelkräfte zusammen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++