TM1 – Statik: Prinzip der virtuellen Arbeit [Definition, Beispiel]

Das Prinzip der virtuellen Arbeit wird häufig verwendet, um unbekannte Lagerkräfte zu bestimmen. Zunächst müssen wir uns mit dem Begriff der Arbeit vertraut machen. Es besagt, dass bei einem sich in Ruhe befindlichen System die virtuelle Arbeit aller äußeren Kräfte und Momente verschwindet.

Wir wollen uns in dieser Lerneinheit anschauen, wie das Prinzip der virtuellen Arbeit angewendet wird.

Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.

In dieser Lektion wollen wir uns das Prinzip der virtuellen Arbeit zur Berechnung von unbekannten Lagerkräften anschauen.

Begriff: Arbeit

Das Prinzip der virtuellen Arbeit wird häufig verwendet, um unbekannte Lagerkräfte zu bestimmen. Zunächst müssen wir uns mit dem Begriff der Arbeit vertraut machen.

Eine Arbeit wird dann verrichtet, wenn eine Kraft F einen Körper über einen Weg s verschiebt. Wirkt die Kraft genau in Richtung des Weges, so ist die Arbeit positiv, wirkt die Kraft genau entgegengesetzt zur Bewegung, dann ist die Arbeit negativ.

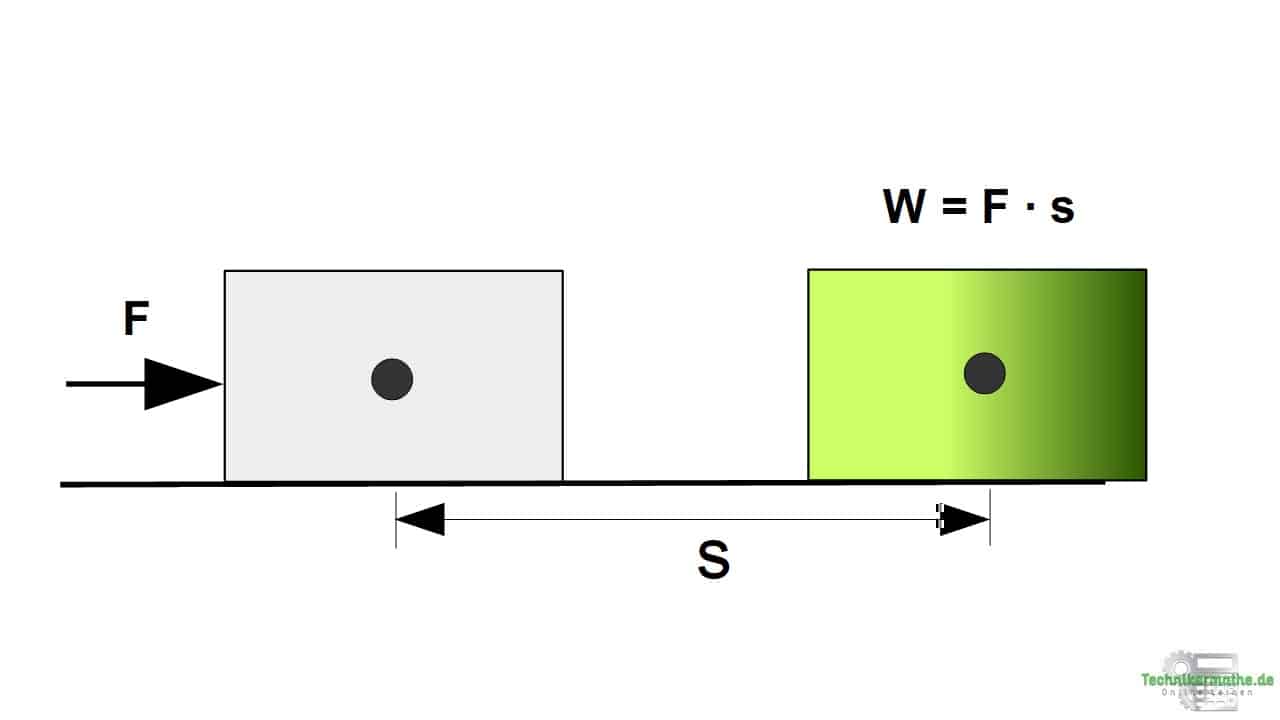
Die Arbeit W ist damit das Produkt aus Kraft mal Weg:

$W = F \cdot s$

Wir befinden uns im obigen Fall innerhalb der Dynamik (Teilgebiet Kinetik), weil wir einen bewegten Körper betrachten.

Merk’s dir!

Beim Prinzip der virtuellen Arbeit gehen wir nun nicht von tatsächlichen Bewegungen bzw. Verschiebungen von Körpern aus, sondern von virtuellen – also gedachten – Verschiebungen.

Prinzip der virtuellen Arbeit: Voraussetzungen

Das Prinzip der virtuellen Arbeit basiert auf bestimmten Voraussetzungen, um korrekt angewendet werden zu können. Hier sind die wichtigsten Voraussetzungen:

Starre Körper: Das Prinzip der virtuellen Arbeit gilt typischerweise für starre Körper oder Systeme von starren Körpern. Starre Körper sind solche, deren Form und Größe sich unter Einwirkung von Kräften nicht verändern.
Statischer oder dynamischer Gleichgewichtszustand: Das System muss entweder in einem statischen Gleichgewichtszustand (wo die Summe aller Kräfte und Momente gleich null ist) oder in einem dynamischen Gleichgewichtszustand (wo sich die Bewegung nicht ändert, wenn die Summe aller Kräfte und Momente gleich null ist) sein.
Virtuelle Verschiebungen: Eine virtuelle Verschiebung ist eine gedachte, infinitesimale Verschiebung eines Systems von seiner Gleichgewichtslage ausgehend.
Reversible Verschiebungen: Reversible Verschiebungen sind Verschiebungen in einem mechanischen System, bei denen das System in seinen ursprünglichen Zustand zurückkehren kann, ohne dass dabei Energie verloren geht oder permanente Veränderungen auftreten.
Elastizitätsfreiheit: In den meisten Anwendungen des Prinzips der virtuellen Arbeit wird angenommen, dass das System elastizitätsfrei ist, d.h. dass es keine Verformungen aufgrund von Spannungen oder Verformungen gibt.

Wenn diese Voraussetzungen erfüllt sind, kann das Prinzip der virtuellen Arbeit angewendet werden, um Gleichgewichtsbedingungen in mechanischen Systemen zu analysieren und Lösungen für verschiedene statische oder dynamische Probleme zu finden.

Prinzip der virtuellen Arbeit: Formel

Betrachten wir nun Verschiebungen u statt des Wegs s, so erhalten wir den Arbeitssatz für Verschiebungen:

$dW = F \cdot du$

Hierbei ist dW die infinitesimale Arbeit die infolge der infinitesimalen Verschiebung du durch die Kraft F erfolgt. Wir ersetzen hier s durch u, weil wir allgemein nicht vom Weg s sondern von Verschiebungen u ausgehen.

Merk’s dir!

Der Begriff >infinitesimal< bedeutet: ins unendlich Kleine gehend! Wir betrachten also sehr kleine, kaum merkbare Verschiebungen und damit Arbeiten. Das >d< vor den Buchstaben zeigt an, dass es sich um infinitesimale Verschiebungen und Arbeiten handelt.

Sind mehrere Kräfte gegeben, so müssen wir die Summe der einzelnen Arbeiten betrachten:

$dW = \sum F_i \cdot du_i$

Da wir von virtuellen Verschiebungen ausgehen, die tatsächlich nicht gegeben sind, ist die verrichtete Arbeit tatsächlich nicht vorhanden und damit Null:

Prinzip der virtuellen Arbeit

$dW = \sum F_i \cdot du_i = 0$

Schauen wir uns nun mal Schritt-für-Schritt an, wie das Prinzip der virtuellen Arbeit (auch: PdvA) angewendet wird, um eine unbekannte Auflagerkraft zu bestimmen.

Vorgehensweise: Prinzip der virtuellen Arbeit

Wir wollen mit dem folgenden Beispiel aufzeigen, wie das Prinzip der virtuellen Arbeiten angewendet wird, um eine unbekannte Auflagerkraft zu bestimmen.

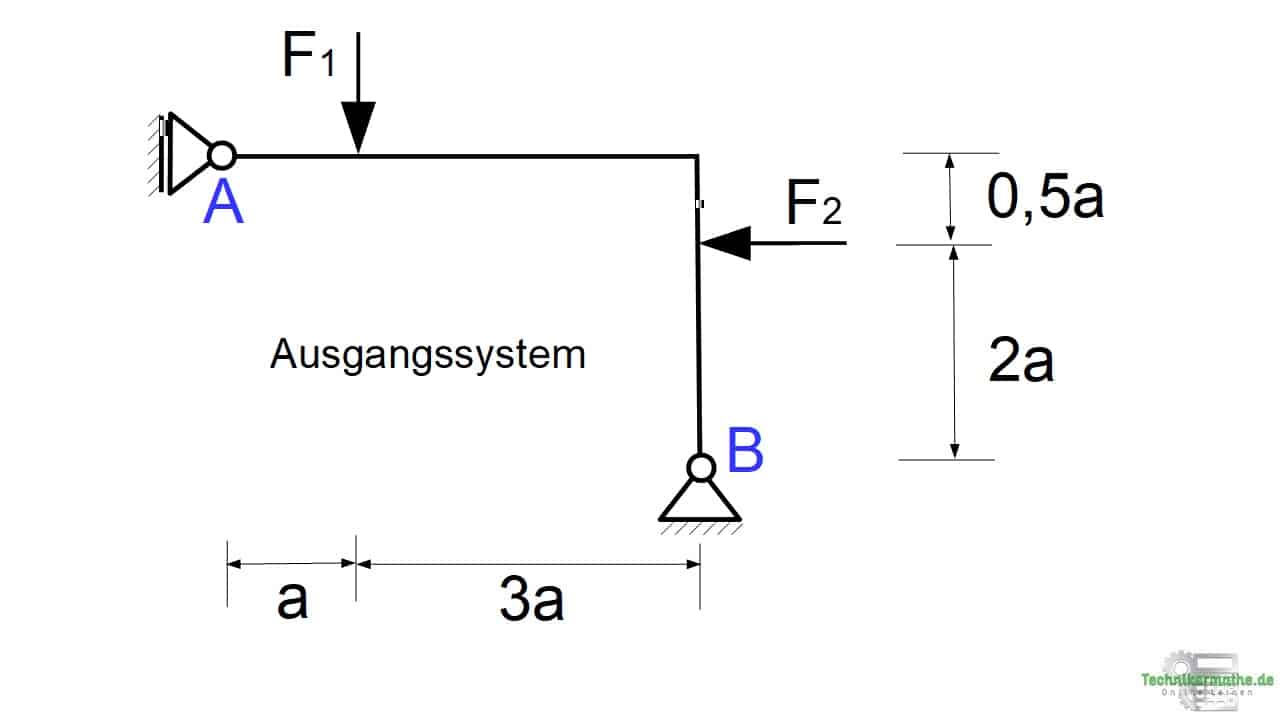
Prinzip der virtuellen Arbeit, pdva, Beispiel, Auflagerkraft berechnen, Verschiebungen, Auflagerkraft, Lagerkraft, virtuelle Verschiebungen — Beispiel: Prinzip der virtuellen Arbeit (PdvA)

Gegeben sei das obige System, welches auf einem Loslager A und einem Festlager B gelagert ist. Die äußeren Kräfte betragen F₁ = 12 kN und F₂ = 8 kN.

Bestimme die Auflagerkraft B_h mittels Prinzip der virtuellen Arbeit.

Schritt 1: Gesuchte Auflagerkraft lösen

Um das Prinzip der virtuellen Arbeit auf statische Systeme anwenden zu können, müssen wir das gegebene statisch bestimmte System zunächst kinematisch also verschieblich machen, indem wir die gesuchte Auflagerreaktion entfernen und als äußere Kraft an das System anbringen.

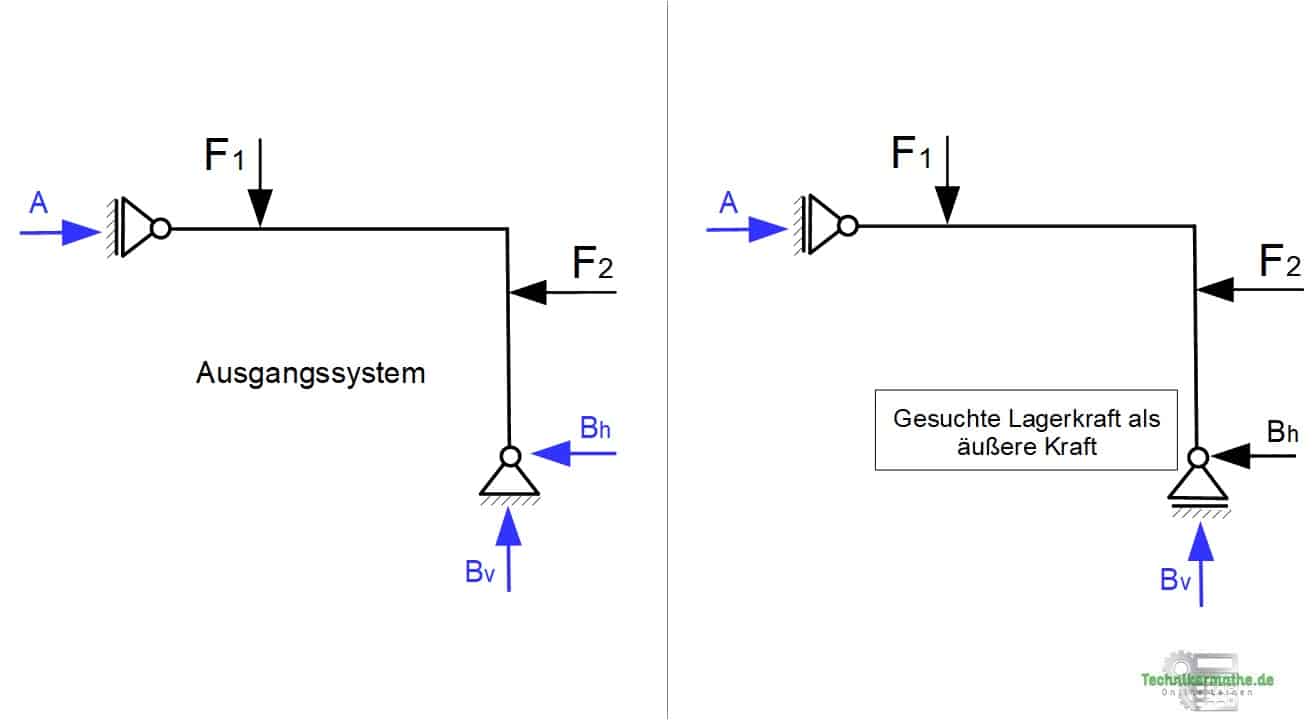
Prinzip der virtuellen Arbeit, PdvA, Auflagerkräfte berechnen, Verschiebungen, Auflagerkraft, Lagerkraft — Gesuchte Auflagerkraft als äußere Kraft abtragen

Gesucht wird die Auflagerkraft B_hmittels Prinzip der virtuellen Arbeit. Demnach müssen wir diese Lagerkraft aus dem System lösen und als äußere Kraft abtragen. Das gegebene Festlager müssen wir dann durch ein Lager ersetzen, welches dann keine vertikale Lagerkraft mehr übertragen darf. Dazu wählen wir ein Loslager, welches noch die vorhandene Lagerkraft B_v überträgt.

Schritt 2: Polplan aufstellen

Prinzip der virtuellen Arbeit, Polplan, Verschiebungen, virtuelle Verschiebung, virtuelle Arbeit, Auflagerkraft, — Polplan aufstellen

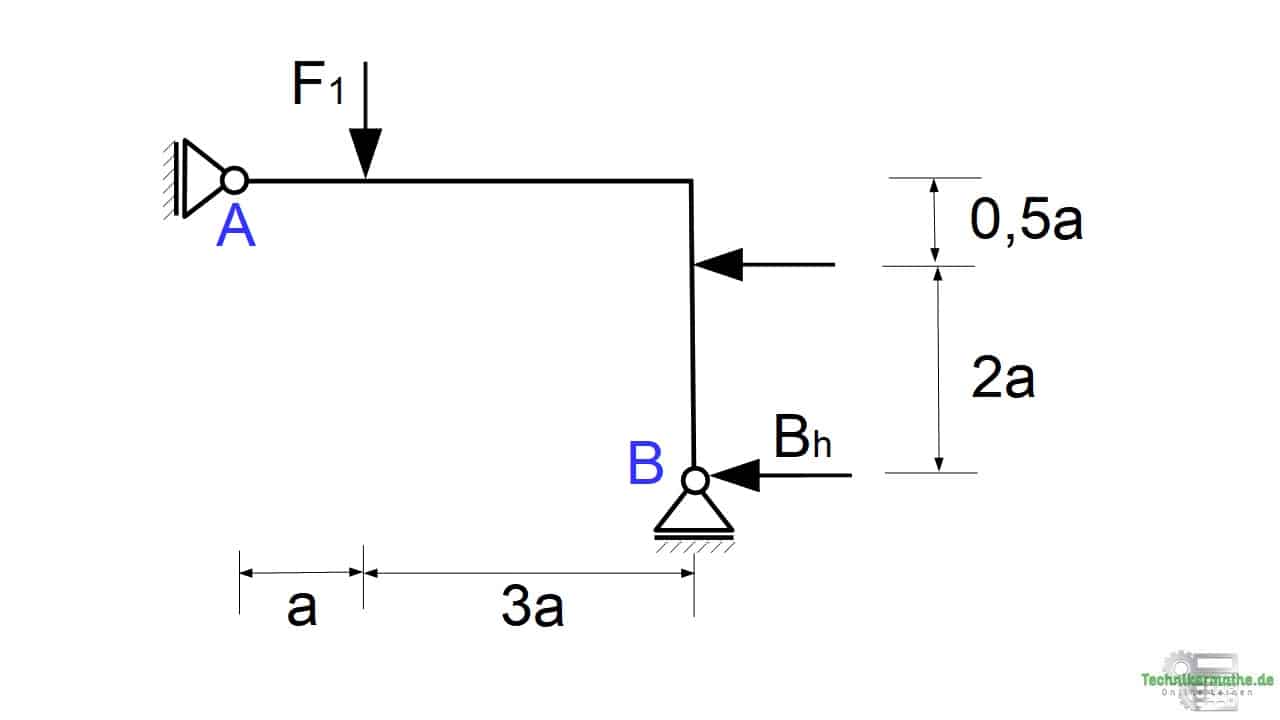
Im nächsten Schritt muss der Polplan aufgestellt werden. Dazu wenden wir die Regeln des Polplans an (siehe Materialien).

Bei unserem System handelt es sich um eine Scheibe, weil dieses System fest verbunden ist. Es sind keine Gelenke gegeben, die zwei Systeme miteinander verbinden.

Damit gibt es hier nur einen Hauptpol und keinen Nebenpol. Wir müssen diesen Hauptpol zunächst finden.

Da wir zwei Loslager (=verschiebliche Lager) gegeben haben, können wir hier die Regel 3 anwenden.

Regel 3: Der Hauptpol (i) einer Scheibe, die auf einem verschieblichen Lager (z.B. Loslager) gelagert ist, liegt auf einer Geraden (Polstrahl) senkrecht zur Bewegungsmöglichkeit dieses Lagers.

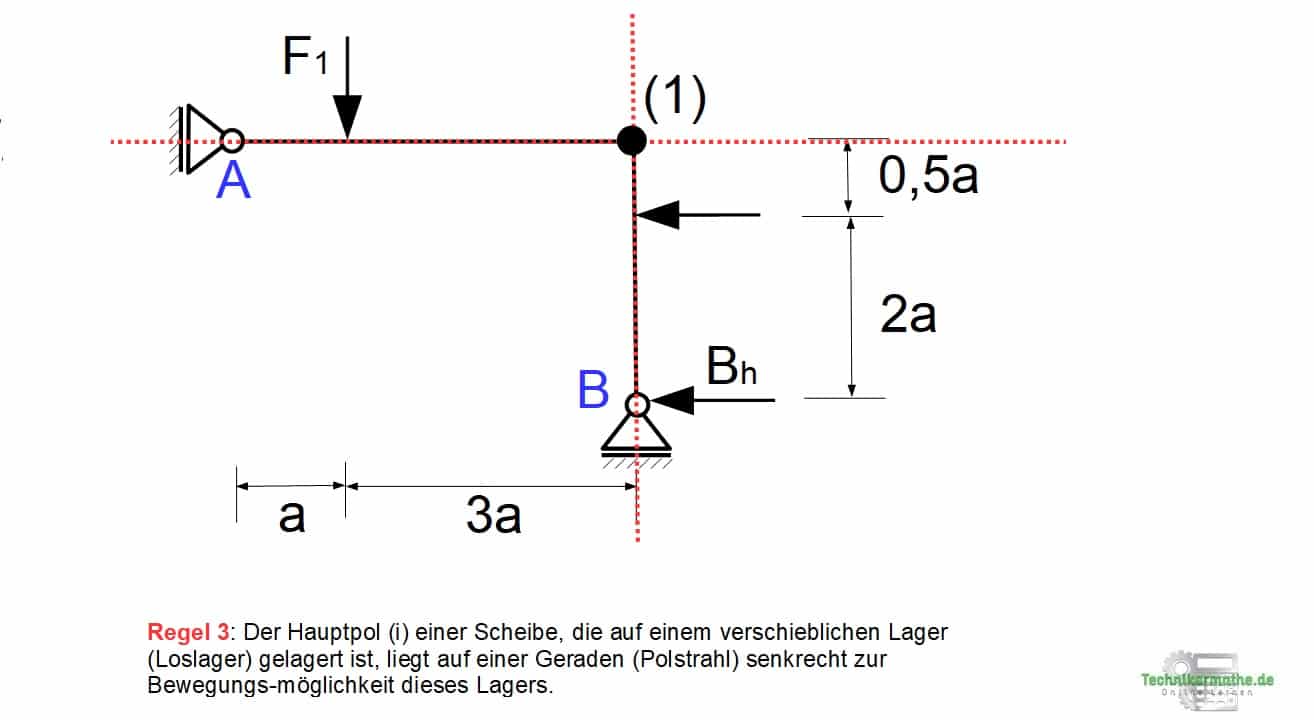
Polplan, Prinzip der virtuellen Arbeit, Verschiebungen, Regel — Polplan anwenden

In der obigen Grafik ist der Hauptpol (1) der Scheibe im Schnittpunkt der beiden Polstrahlen gegeben. Denn für diesen Punkt gilt die Regel 3 für beide Loslager.

Schritt 3: Verschiebungsplan

Als nächstes betrachten wir den Verschiebungsplan, indem wir eine infinitesimale Drehung dφ um den Hauptpol vornehmen. Hier können wir nun entweder eine Drehung im oder entgegengesetzt zum Uhrzeigersinn wählen.

Merk’s dir!

Der Begriff >infinitesimal< bedeutet >ins unendlich Kleine gehend<. Wir gehen hier also von sehr kleinen, kaum sichtbaren Drehungen und damit verbundenen Verschiebungen aus. Diese Drehungen und Verschiebungen sind zudem virtuell, also gedacht und dienen lediglich der Berechnung der Auflagerkräfte.

Wir wählen hier eine infinitesimale Drehung dφ im Uhrzeigersinn (Rechtsdrehung) um den Hauptpol (1):

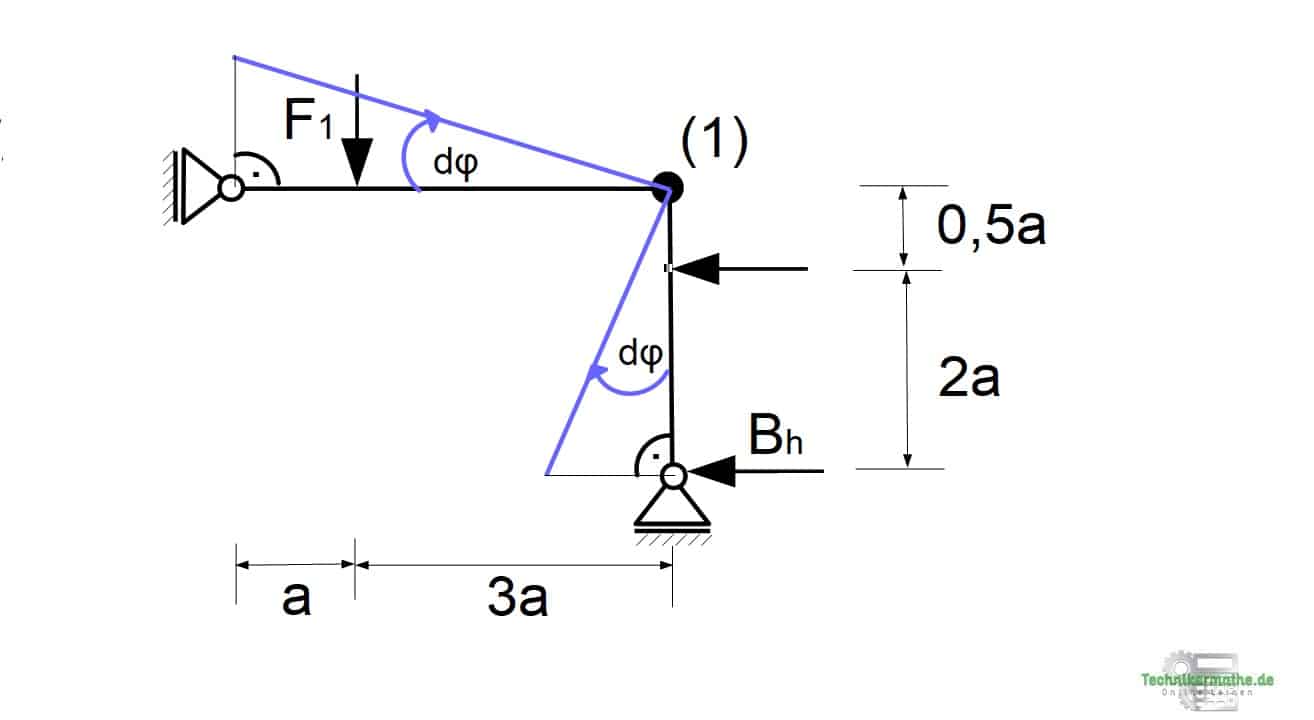
Prinzip der virtuellen Arbeit, Verschiebungsplan, Drehung, Polplan — Infinitesimale Drehung des Systems im Uhrzeigersinn

Durch die infinitesimale Drehung um den Hauptpol erfolgt eine Verschiebung der Endpunkte (hier: Auflager) in einem rechten Winkel zur Verbindungslinie zwischen Hauptpol und Endpunkt.

Das System verschiebt sich dann wie in der Grafik in blau angegeben. Dabei verschieben sich auch die Loslager sowie die Kräfte F₁, F₂ und B_h:

Prinzip der virtuellen Arbeit, Verschiebungsplan, Verschiebung — Verschiebung der Auflager und Kräfte

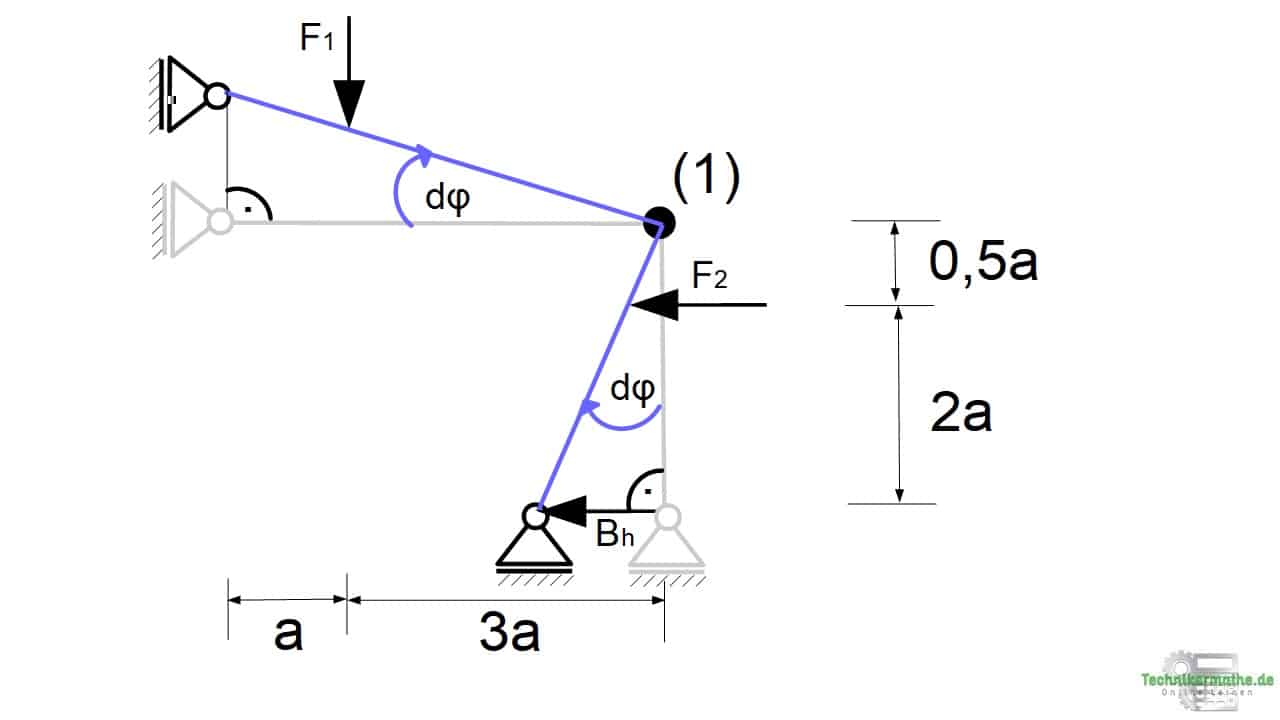
Wir wollen nun die aufgrund der virtuellen infinitesimalen Verdrehung dφ hervorgerufenen infinitesimalen Verschiebungen du der einzelnen Kräfte bestimmen. Dazu betrachten wir die rechtwinkligen Dreiecke und wenden den Tangens an (Trigonometrie am rechtwinkligen Dreieck):

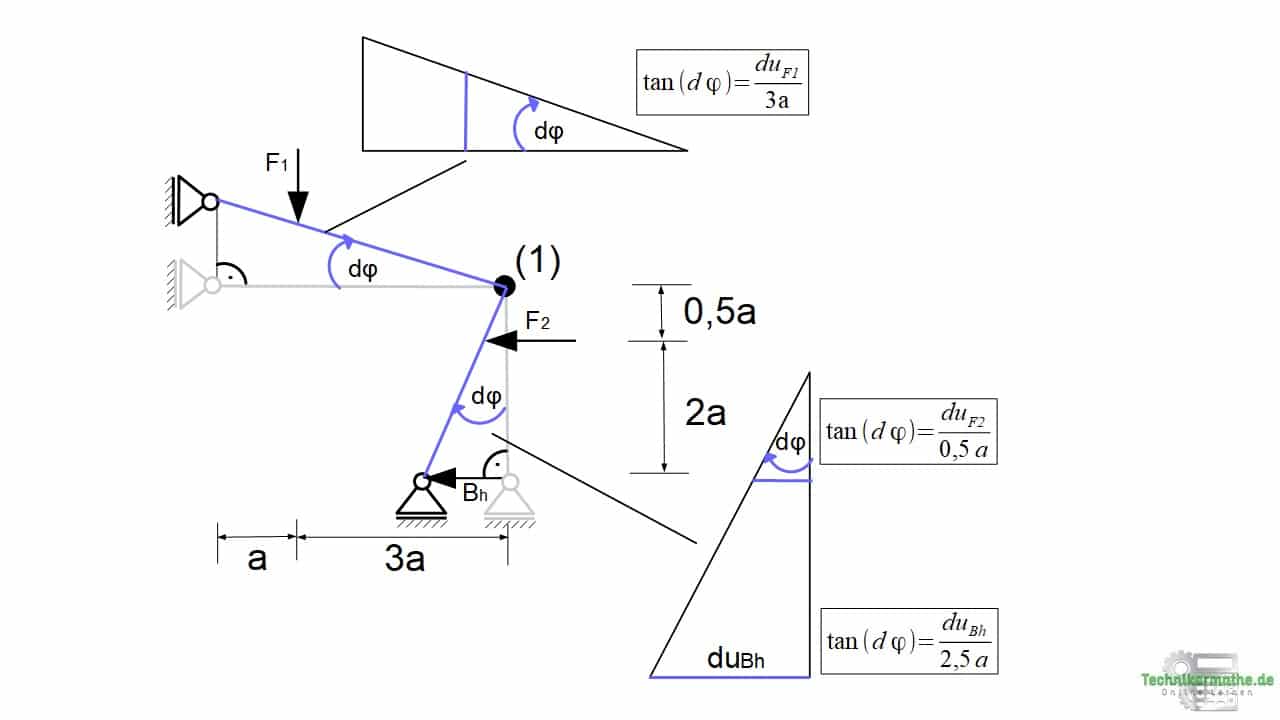
Prinzip der virtuellen Arbeit, Verschiebungsplan, Verschiebung, Tangens — Berechnung der Verschiebung der äußeren Kräfte

Wir gehen hier von infinitesimalen Verschiebungen aus, weshalb gilt:

$\tan(d\varphi) = d\varphi$

Merk’s dir!

Der Tangens des Winkels ist bei sehr kleinen Winkel gleich dem Winkel selbst.

Damit ergib sich:

$d\varphi = \dfrac{du_{F1}}{3a}$

$d\varphi = \dfrac{du_{F2}}{0,5a}$

$d\varphi = \dfrac{du_{Bh}}{2,5a}$

Wir suchen die infinitesimale Verschiebung du der Kräfte infolge der infinitesimalen Drehung dφ um den Hauptpol und lösen die obigen Gleichungen nach der Verschiebung auf:

$du_{F1} = d\varphi \cdot 3a$ Verschiebung der Kraft F₁

$du_{F2} = d\varphi \cdot 0,5a$ Verschiebung der Kraft F₂

$du_{Bh} = d\varphi \cdot 2,5a$ Verschiebung der Kraft B_h

Schritt 4: Arbeitssatz anwenden und Lagerkraft berechnen

Prinzip der virtuellen Arbeit, Verschiebungsplan, Arbeitssatz, Verschiebungen — Arbeitssatz anwenden, um Verschiebungen zu berechnen

Im nächsten Schritt wenden wir den Arbeitssatz an:

$dW = \sum F_i \cdot du = 0$

dW ist hierbei die Summe der infinitesimale Arbeit, die von den Kräfte auf ihren infinitesimalen Verschiebungen du verrichtet wird.

Diese infinitesimale Arbeit dW setzen wir gleich Null, weil tatsächlich im System keine Verschiebungen stattfinden dürfen. Diese haben wir nur herbeigeführt, indem wir die Auflagerkraft B_h entfernt und als äußere Kraft abgetragen haben. Mit der Bedingung, dass nun die Arbeit null sein muss, können wir diese unbekannte Kraft B_h berechnen.

Die Verschiebungen hatten wir berechnet zu:

$du_{F1} = d\varphi \cdot 3a$ Verschiebung der Kraft F₁

$du_{F2} = d\varphi \cdot 0,5a$ Verschiebung der Kraft F₂

$du_{Bh} = d\varphi \cdot 2,5a$ Verschiebung der Kraft B_h

Einsetzen der Verschiebungen in den Arbeitssatz:

$dW = -F_1 \cdot d\varphi \cdot 3a + F_2 \cdot d\varphi \cdot 0,5a + B_h \cdot d\varphi \cdot 2,5a= 0$

Die Arbeit, welche die Kraft F₁ verrichtet ist negativ, weil die Kraft F₁ entgegengesetzt zur Verschiebung gerichtet ist. Die Verschiebung erfolgt vertikal nach oben, die Kraft F₁ ist aber vertikal nach unten gerichtet.

Die Arbeiten, welche die Kräfte F₂ und B_h verrichten sind positiv, weil die Kräfte und die Verschiebung gleich gerichtet sind.

Wir lösen nun die obige Gleichungen Schritt-für-Schritt nach der gesuchten Lagerkraft B_h auf:

$-F_1 \cdot d\varphi \cdot 3a + F_2 \cdot d\varphi \cdot 0,5a + B_h \cdot d\varphi \cdot 2,5a= 0$ | $:d\varphi$

$-F_1 \cdot 3a + F_2 \cdot 0,5a + B_h \cdot 2,5a= 0$

$B_h \cdot 2,5 = F_1 \cdot 3 - F_2 \cdot 0,5$ | $:2,5a$

$B_h = F_1 \cdot 1,2 - F_2 \cdot 0,2$

Einsetzen der Zahlenwerte (F₁ = 12 kN, F₂ = 8 kN):

$B_h = 12 kN \cdot 1,2 - 8 kN \cdot 0,2 = 12,8 kN$

Die Auflagerkraft B_h beträgt 12,7 kN.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++