TM1 – Knotenpunktverfahren

Das Knotenpunktverfahren dient zur Berechnung der unbekannten Stabkräfte in einem Fachwerk. Dazu schneidest du jeden Knoten einzeln frei und bestimmst aus der vertikalen und horizontalen Gleichgewichtsbedingung die unbekannten Stabkräfte. Es ist immer nur möglich einen Knoten mit maximal 2 unbekannten Stabkräften zu betrachten.

In diesem Kursabschnitt erklären wir dir ausführlich und einfach anhand eines Beispiels wie das Knotenpunktverfahren funktioniert. Dieser Lerntext ist ein Auszug aus unserem Onlinekurs TM1 – Statik.

Für ein optimales Verständnis zeigen wir die das Knotenpunktverfahren an einem ausführlichen Beispiel auf.

Knotenpunktverfahren – Grundlagen

Das Knotenpunktverfahren dient zur Berechnung der unbekannten Stabkräfte in einem Fachwerk. Dazu schneidest du jeden Knoten einzeln frei und bestimmst aus der vertikalen und horizontalen Gleichgewichtsbedingung die unbekannten Stabkräfte. Es ist immer nur möglich einen Knoten mit maximal 2 unbekannten Stabkräften zu betrachten.

In dieser Lerneinheit behandeln wir das Knotenpunktverfahren zur Bestimmung der unbekannten Stabkräfte in einem Fachwerk. Wir betrachten hierzu ein ausführliches Beispiel zur Anwendung des Knotenpunktverfahrens. Wir zeigen dir in diesem Beispiel:

Wie du die Nullstäbe bestimmst.
Wie du die Auflagerkräfte berechnest.
Wie du die Winkel von den Stabkräften zur Waagerechten mittels Trigonometrie bestimmst.
Wie du die Stabkräfte aus den Gleichgewichtsbedingungen mittels Knotenpunktverfahren ermittelst.

Knotenpunktverfahren – Beschreibung | Gleichungen

Das Knotenpunktverfahren dient zur Bestimmung aller Stabkräfte eines Fachwerks. Dazu wird jeder Knoten freigeschnitten und die Gleichgewichtsbedingung in x-und y-Richtung angewendet, um die unbekannten Stabkräfte an diesem Knoten zu bestimmen. Die Knoten müssen sich alle im Gleichgewicht befinden, d.h. die Summe aller Kräfte in x- und in y-Richtung muss Null ergeben.

Gleichgewichtsbedingungen:

$\sum S_{ix} = 0$ Summe aller Kräfte in x-Richtung muss Null ergeben

$\sum S_{iy} = 0$ Summe aller Kräfte in y-Richtung muss Null ergeben

Die Momentengleichgewichtsbedingung entfällt, da die Knoten keine Momente übertragen und die Stäbe zentrisch an den Knoten angeschlossen sind.

Eine an den Knoten wirkende äußere Kraft muss ebenfalls mit ihrer gegebenen Richtung berücksichtigt werden. Für die Stabkräfte selber ist zwar die Wirkungslinie der Stäbe bekannt und wird übernommen, aber nicht die Wirkrichtung (Zug- oder Druckstab). Deswegen werden alle Stäbe zunächst als Zugstäbe angenommen. Das spätere Ergebnis zeigt dann die tatsächliche Wirkrichtung an. Bei einem negativen Wert ist tatsächlich ein Druckstab gegeben. Bei einem positiven Wert ist die angenommen Richtung bestätigt und es handelt sich um einen Zugstab.

Knoten freischneiden, Knotenpunktverfahren, Stabkräfte, äußere Kraft, Beispiel — Knotenpunktverfahren

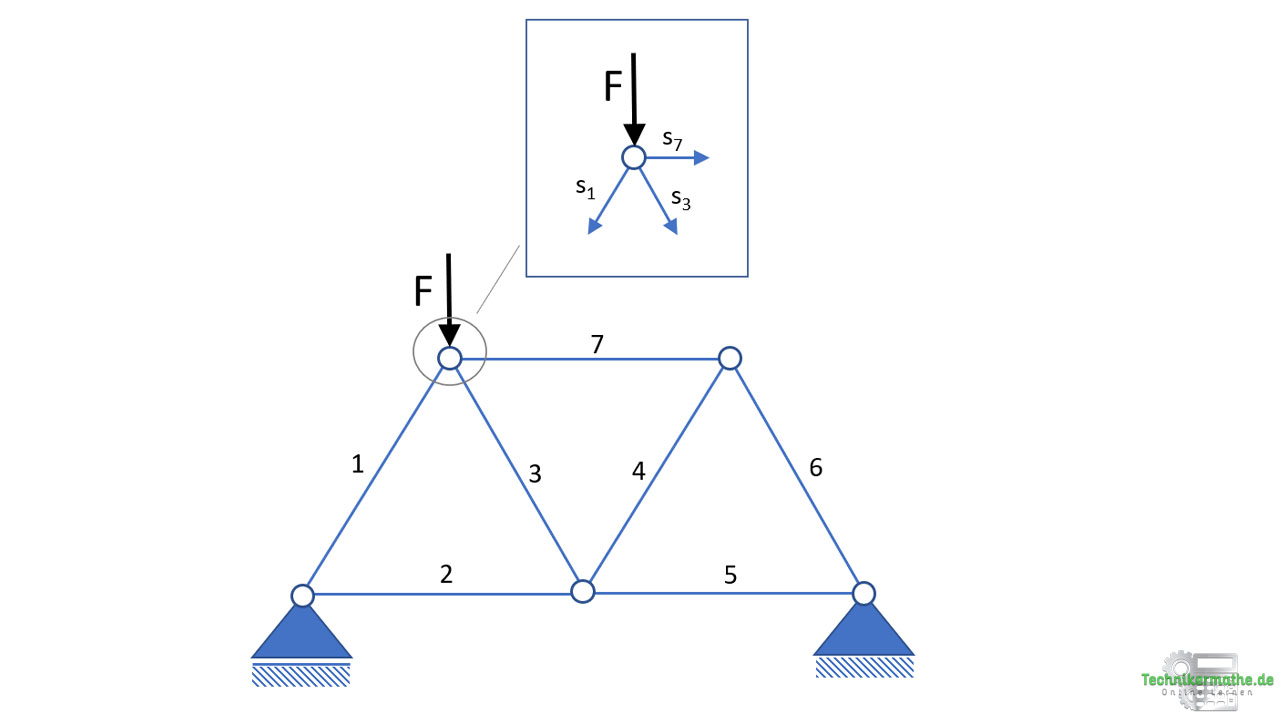
Es wird immer nur derjenige Knoten freigeschnitten der maximal zwei unbekannte Stabkräfte aufweist, weil aus den beiden Gleichgewichtsbedingungen nur zwei unbekannte Kräfte berechnet werden können. In der obigen Grafik kann der freigeschnittene Knoten also erst dann betrachtet werden, wenn mindestens einer der Stabkräfte (S₁, S₂ oder S₃) bereits bekannt ist.

Knotenpunktverfahren an einem Beispiel

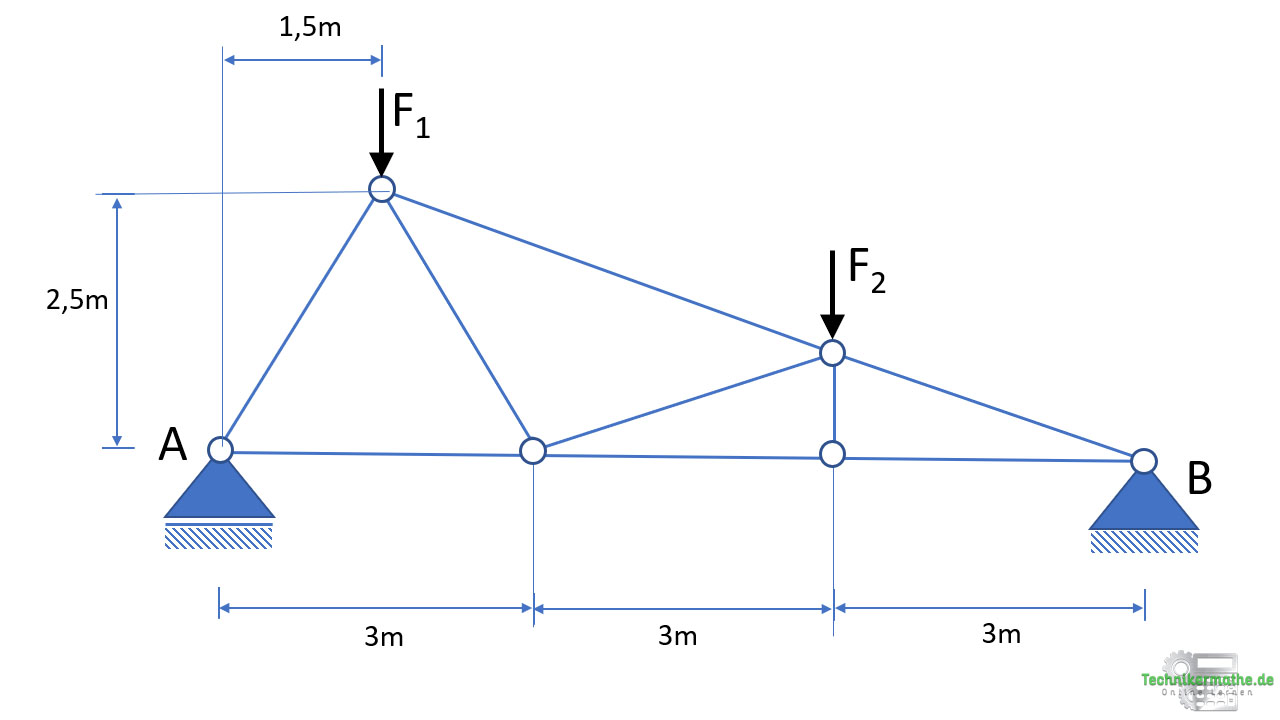
Wir wollen uns das Knotenpunktverfahren mal an einem ausführlichen Beispiel anschauen:

Aufgabenstellung

In der obigen Grafik siehst du ein Fachwerk, welches auf einem Loslager A und einem Festlager B gelagert ist. Auf das Fachwerk wirken die beiden äußeren Kräfte F₁ = 50 kN und F₂ = 20 kN. Gesucht werden

a) die Auflagerkräfte (Stützkräfte) und

b) alle Stabkräfte des Fachwerks mittels Knotenpunktverfahren.

Nullstäbe bestimmen

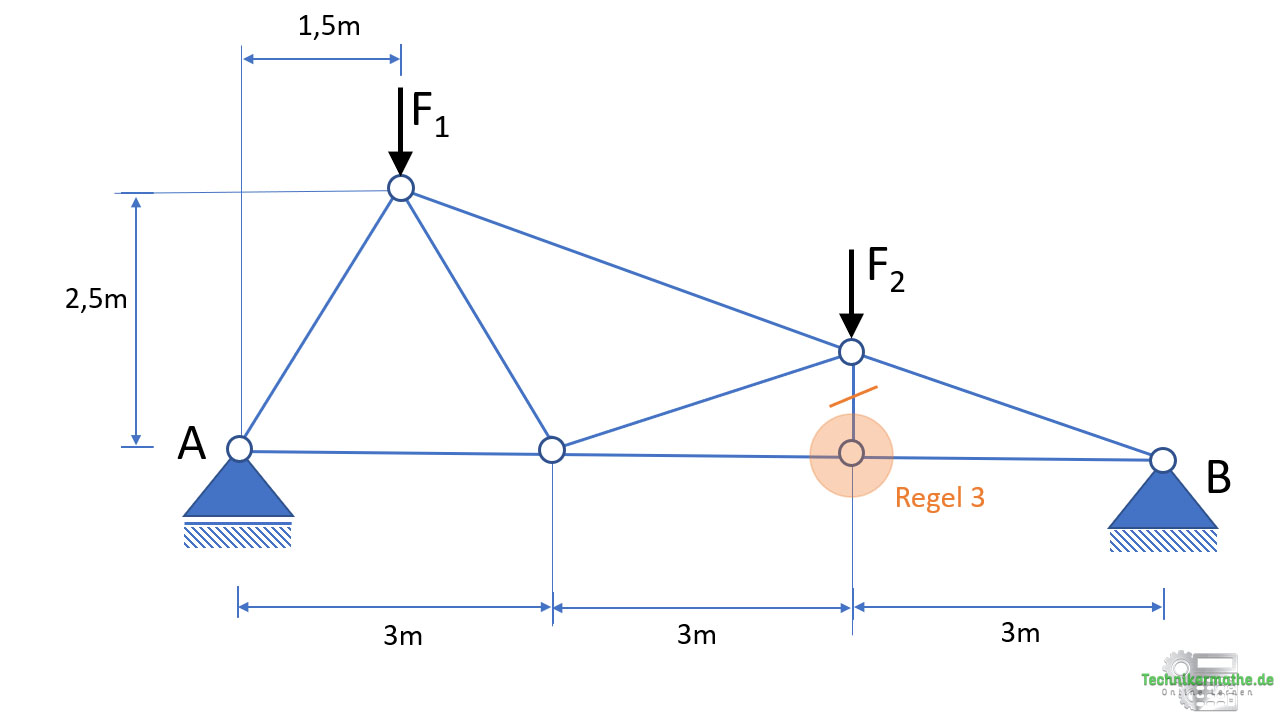
Wir starten zunächst mit der Bestimmung von Nullstäben im obigen Fachwerk:

Im obigen Fachwerk kann für den markierten Knoten die Regel 3 angewendet werden. Hier greifen drei Kräfte an einen unbelasteten Knoten an. Zwei liegen auf einer Wirkungslinie, dann ist der dritte ein Nullstab. Diesen Nullstab markieren wir für die weiteren Berechnungen.

Hinweis Regel 1 bzw. 2

Der Knoten im Lager A weist zwar zwei Stäbe auf, die in unterschiedliche Richtung wirken, jedoch greift hier die Lagerkraft A an. Deswegen ist hier ein belasteter Knoten gegeben. Selbes gilt für den Knoten am Lager B. Damit können wir die Regel 2 überprüfen.

Für das Loslager A wissen wir, dass es eine vertikale Lagerkraft ist, wir kennen also die Richtung dieser äußeren Kraft. Da aber kein Stab im Lager A vertikal gerichtet ist, können wir die Regel 2 hier nicht anwenden.

Für das Festlager B hingegen kennen wir zwar die einzelnen Kräfte B_h und B_v, allerdings müssen wir die resultierende Lagerkraft B betrachten. Wie genau die resultierende Lagerkraft B wirkt, wissen wir nicht. Deswegen können wir hier die Regel gar nicht anwenden.

Stäbe und Knoten durchnummerieren

Zunächst müssen alle Stäbe und Knoten durchnummeriert werden, damit wir genau wissen, welchen Stab wir schon berechnet haben bzw. noch berechnen müssen und an welchem Knoten wir uns gerade befinden. Für die Knoten wählen wir römische Zahlen:

Knotenpunkverfahren, Beispiel — Knotenpunktverfahren

Fachwerk freischneiden und Auflagerkräfte berechnen

Im nächsten Schritt müssen wir das Fachwerk von den Auflagern freischneiden und die unbekannten Auflagerkräfte abtragen:

Knotenpunktverfahren, Lagerkräfte berechnen — Knotenpunktverfahren

Die Auflagerkräfte können wir mit den drei Gleichgewichtsbedingungen der Ebene berechnen:

$\sum F_{ix} = 0$

$\sum F_{iy} = 0$

$\sum M_i = 0$

Wir starten mit der Gleichgewichtsbedingung in x-Richtung. Da keine äußeren horizontalen Kräfte an das Fachwerk angreifen, ist die horizontale Auflagerkraft B_h gleich Null:

$\sum F_{ix} = 0: \; B_h = 0$

Als nächstes wenden wir die Gleichgewichtsbedingung in y-Richtung an, indem wir alle vertikalen Kräfte summieren. Kräfte die nach oben zeigen berücksichtigen wir positiv, Kräfte die nach unten zeigen negativ:

$\sum F_{iy} = 0: \; \; A - F_1 - F_2 + B_v = 0$

Wir haben hier zwei unbekannte Kräfte A und B_v gegeben. Wir können aus dieser Gleichung also noch keine Unbekannte bestimmen. Demnach betrachten wir als nächstes die Momentengleichgewichtsbedingung und wählen den Bezugspunkt so, dass eine unbekannte Kraft aus der Berechnung herausfällt. Dazu legen wir den Bezugspunkt genau in den Angriffspunkt der unbekannten Kraft. Wir wählen beliebig das Lager A:

$\sum M_i^A = 0: \; \; -F_1 \cdot 1,5 m - F_2 \cdot 6m + B_v \cdot 9m = 0$

Wir lösen die obige Gleichung nach der Auflagerkraft B_v auf:

$B_v = \dfrac{F_1 \cdot 1,5 m + F_2 \cdot 6m}{9m}$

Einsetzen der gegeben Werte führt uns zu:

$B_v = \dfrac{50 kN \cdot 1,5 m + 20 kN \cdot 6m}{9m} = 21,67 kN$

Die Auflagerkraft B_v muss insgesamt 21,67 kN aufnehmen, damit das Fachwerk sich nicht vertikal verschiebt.

Um herauszufinden wie viel die Auflagerkraft A aufnehmen muss, können wir nun die vertikale Gleichgewichtsbedingung heranziehen und nach A auflösen:

$A - F_1 - F_2 + B_v = 0$

$A = F_1 + F_2 - B_v = 50 kN + 20 kN - 21,67 kN = 48,33 kN$

Die Auflagerkraft A muss 48,33 kN aufnehmen, damit sich das Fachwerk nicht vertikal verschiebt.

Zusammenfassung der Auflagerkräfte

Auflagerkraft	A	B_h	B_v
Betrag	48,33 kN	0	21,67 kN

Knoten freischneiden und Stabkräfte berechnen

Nachdem wir die Nullstäbe bestimmt und die Auflagerkräfte berechnet haben, können wir mit dem Knotenpunktverfahren beginnen. Dazu schneiden wir die einzelnen Knoten frei und berechnen die unbekannten Stabkräfte. Wichtig ist hierbei, dass wir nur diejenigen Knoten betrachten können, an denen maximal zwei unbekannte Stabkräfte angreifen. Wir beginnen mit dem Knoten I, weil hier nur zwei unbekannte Stabkräfte gegeben sind.

Knoten I

Zunächst müssen wir mittels Trigonometrie am rechtwinkligen Dreieck den Winkel vom Stab 1 zur Horizontalen bestimmen:

Knotenpunktverfahren, Trigonometrie, Fachwerk, Tangens — Knotenpunktverfahren

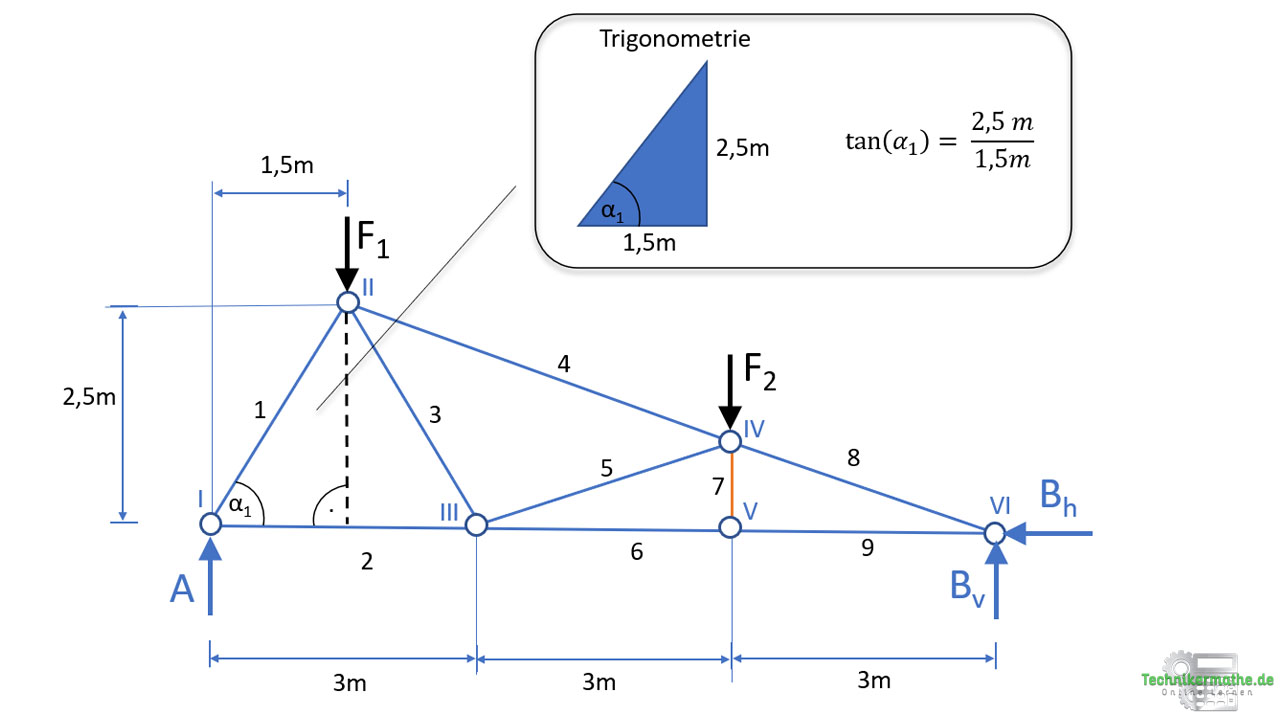
Wir konstruieren hierzu ein rechtwinkliges Dreieck, indem wir die Höhe (gestrichelte senkrechte Linie) einfügen. Wir haben dann aus dem allgemeinen Dreieck zwei rechtwinklige Dreiecke gemacht. Für das linke Dreieck berechnen wir den Winkel α₁ mittels Tanges, da wir die Gegenkathete (Höhe 2,5m) sowie die Ankathete (1,5m) gegeben haben:

$\tan(\alpha_1) = \dfrac{2,5m}{1,5m}$

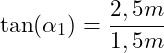
Auflösen nach $\alpha_1$ :

$\alpha_1 = \tan^{-1}(\dfrac{2,5m}{1,5m})$

$\alpha_1 = 59,04^{\circ}$

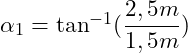
Jetzt können wir den Knoten I freischeiden und die Kräfte antragen:

Knotenpunktverfahren, Knoten I, Fachwerk, unbekannte Stabkräfte — Knotenpunktverfahren

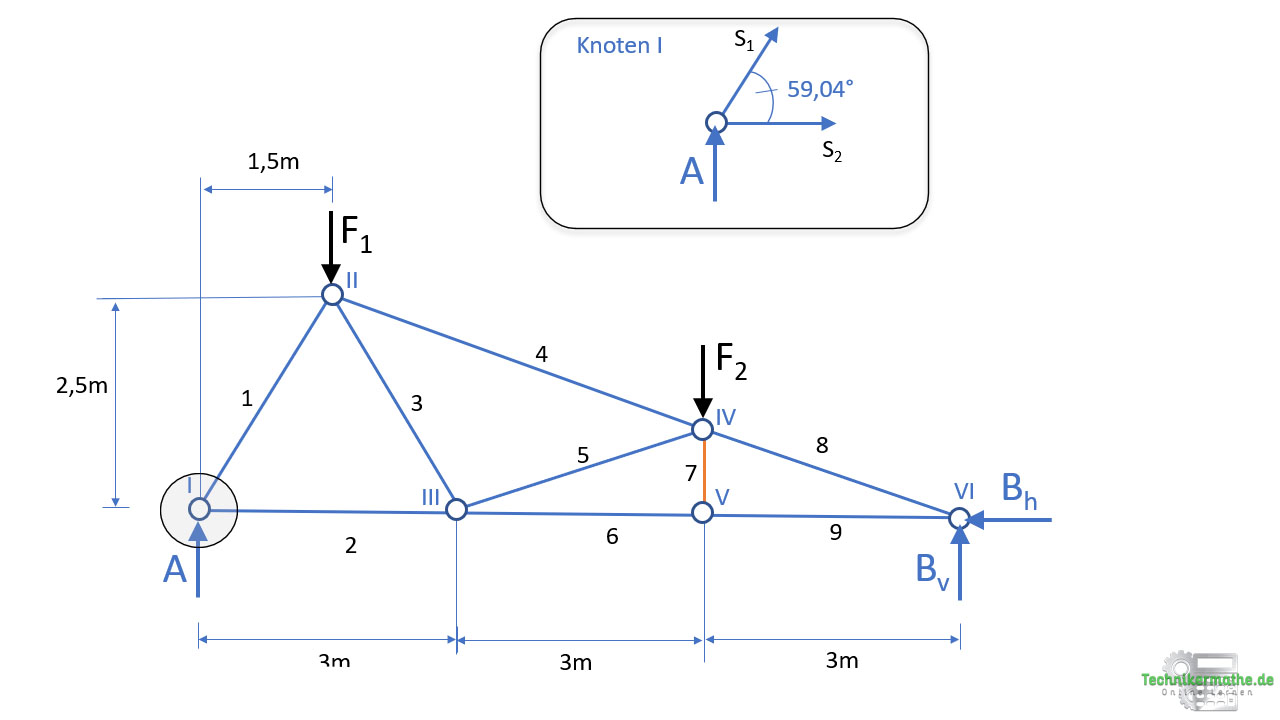
Zur Berechnung der unbekannten Stabkräfte wenden wir die Gleichgewichtsbedingungen in x- und y-Richtung an.

Wir starten mit der Gleichgewichtsbedingung in y-Richtung:

$\sum F_{ix} = 0: \; \; S_1 \cdot \cos(59,04^{\circ}) + S_2 = 0$

Die Stabkraft S₁ muss hier in ihre x-Komponente zerlegt werden. Da der Winkel zur Waagrechten gegeben ist, bestimmen wir die x-Komponente mittels Kosinus. Beide Kräfte sind positiv zu berücksichtigen, da sie nach rechts in positive x-Richtung zeigen.

Wir berechnen den cos(59,04°):

$S_1 \cdot 0,514 + S_2 = 0$

Aus der obigen Gleichung können wir noch keine Stabkraft berechnen, deswegen schauen wir uns die Gleichgewichtsbedingung in y-Richtung an:

$\sum F_{iy} = 0: \; \; S_1 \cdot \sin(59,04^{\circ}) + A = 0$

Die Stabkraft S₁ muss hier in ihre y-Komponente zerlegt werden. Da der Winkel zur Waagrechten gegeben ist, bestimmen wir die y-Komponente mittels Sinus. Beide Kräfte sind positiv zu berücksichtigen, da sie nach oben in positive y-Richtung zeigen.

Wir berechnen zunächst den sin(59,04°):

$S_1 \cdot 0,858 + A = 0$

Wir können nun die obige Gleichung nach S₁ auflösen:

$S_1 \cdot 0,858 = -A$

$S_1 = -\dfrac{A}{0,858}$

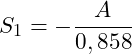
Einsetzen von A = 48,33 kN ergibt:

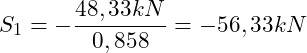$S_1 = -\dfrac{48,33 kN}{0,858} = -56,33 kN$ (Druckstab)

Die Stabkraft S₁ ist 56,33 kN groß. Das Vorzeichen gibt an, dass es sich um einen Druckstab handelt, der zum Knoten hinzeigt.

Betrachten wir nun wieder die horizontale Gleichgewichtsbedingung, so können wir auch die Stabkraft für S₂ berechnen:

$S_1 \cdot 0,514 + S_2 = 0$

Auflösen nach S₂ und einsetzen der Werte:

$S_2 = -S_1 \cdot 0,514$

$S_2 = -(-56,33 kN) \cdot 0,514 = 28,95 kN$ (Zugstab)

Die Stabkraft S₂ ist 28,95 kN groß. Das Vorzeichen gibt an, dass es sich um einen Zugstab handelt, der wie angenommen vom Knoten wegzeigt.

Knoten II

Zunächst müssen wir den Winkel von der Stabkraft S₄ zur Waagerechten bestimmen. Den Winkel von der Stabkraft S₁ zur Waagerechten haben wir bereits oben bestimmt:

Knotenpunktverfahren, Trigonometrie, Winkel — Knotenpunktverfahren

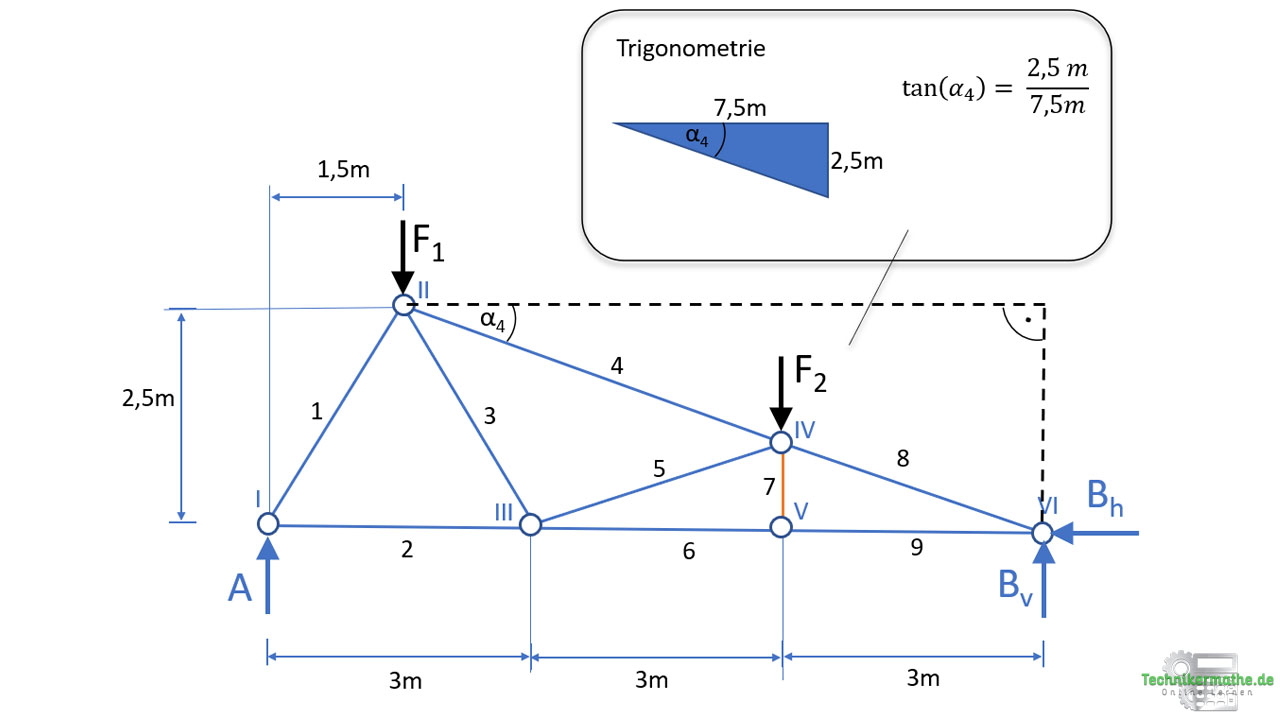
Zur Bestimmung des Winkels von S₄ zur Waagrechten müssen wir das äußere rechtwinklige Dreieck (gestrichelte Linie) konstruieren. Wir kennen die Höhe mit 2,5m sowie die Länge mit 1,5m + 3m + 3m = 7,5 m. Die 1,5m sind der Teil vom ersten (linken) Dreieck des Fachwerks.

Auch hier wenden wir den Tangens an, weil Gegenkathete (Höhe) und Ankathete (Länge) gegeben sind:

$\tan(\alpha_4) = \dfrac{2,5m}{7,5m}$

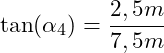
Auflösen nach dem gesuchten Winkel:

$\alpha_4 = \tan^{-1} (\dfrac{2,5m}{7,5m})$

$\alpha_4 = 18,43^{\circ}$

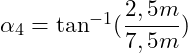
Wir müssen nun noch den Winkel von der Stabkraft S₃ zur Waagerechten bestimmen. Dazu verwenden wir wieder das erste Dreieck und zeichnen die Höhenlinie (gestrichelt) ein:

Trigonometrie, Fachwerke, Winkel — Knotenpunktverfahren

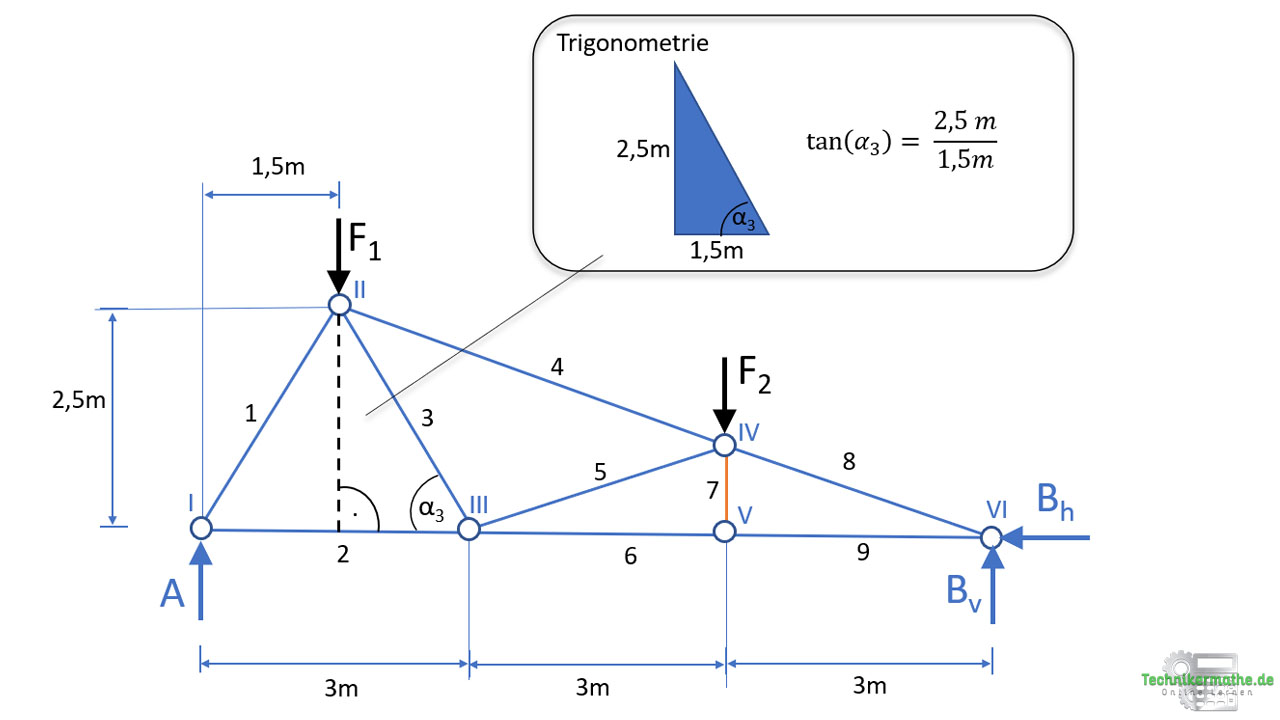
Wir erhalten dann:

$\tan(\alpha_3) = \dfrac{2,5m}{1,5m}$

$\alpha_3 = \tan^{-1} (\dfrac{2,5m}{1,5m})$

$\alpha_3 = 59,04^{\circ}$

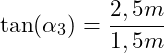
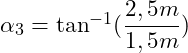
Da wir im ersten Dreieck ein gleichschenkliges Dreieck gegeben haben (siehe Abmessungen) sind die unteren beiden Winkel $\alpha_1 = \alpha_3$ gleich groß!

Als nächstes können wir den Knoten II freischneiden:

Knotenpunktverfahren, Knoten 2, Freischnitt, Gleichgewichtsbedingungen — Knotenpunktverfahren

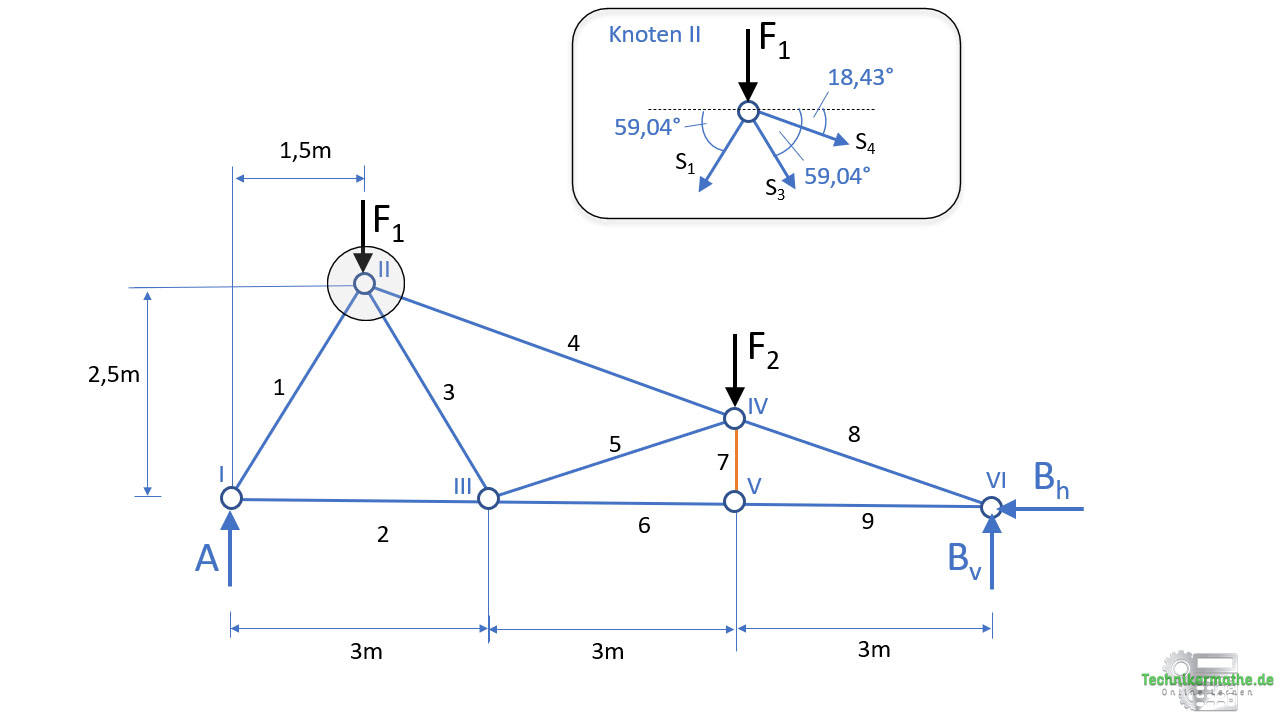
Wir haben nun den Knoten II freigeschnitten und wenden auf diesen die Gleichgewichtsbedingungen an. Wir starten mit der Gleichgewichtsbedingung in x-Richtung:

$\sum F_{ix} = 0: \; \; -S_1 \cdot \cos(59,04^{\circ}) + S_3 \cdot \cos(59,04^{\circ}) + S_4 \cdot \cos(18,43^{\circ}) = 0$

$-S_1 \cdot \cos(59,04^{\circ}) + S_3 \cdot \cos(59,04^{\circ}) + S_4 \cdot \cos(18,43^{\circ}) = 0$

Wir können aus dieser Gleichung noch keine unbekannte Kraft berechnen, wir setzen aber die bekannten Werte ein und fassen die zu berechnenden Werte zusammen (S₁ = -56,33 kN):

$-(-56,33 kN) \cdot \cos(59,04^{\circ}) + S_3 \cdot \cos(59,04^{\circ}) + S_4 \cdot \cos(18,43^{\circ}) = 0$

(I) $28,98 kN + S_3 \cdot 0,514 + S_4 \cdot 0,949 = 0$

Als nächstes Stellen wir die Gleichgewichtsbedingung in y-Richtung auf:

$\sum F_{iy} = 0: \; \; -F_1 - S_1 \cdot \sin(59,04^{\circ}) - S_3 \cdot \sin(59,04^{\circ}) - S_4 \cdot \sin(18,43^{\circ}) = 0$

$-F_1 - S_1 \cdot \sin(59,04^{\circ}) - S_3 \cdot \sin(59,04^{\circ}) - S_4 \cdot \sin(18,43^{\circ}) = 0$

Auch hier können wir keine der unbekannten Kräfte bestimmen, weshalb wir diese Gleichung zunächst komprimieren, indem wir alle Werte berechnen, die berechnet werden können (F₁ = 50 kN, S₁ = -56,33 kN):

$-50 kN - (-56,33 kN) \cdot \sin(59,04^{\circ}) - S_3 \cdot \sin(59,04^{\circ}) - S_4 \cdot \sin(18,43^{\circ}) = 0$

$-50 kN + 48,30 kN - S_3 \cdot 0,858 - S_4 \cdot 0,316 = 0$

(II) $-1,7 kN - S_3 \cdot 0,858- S_4 \cdot 0,316 = 0$

Wir lösen eine der beiden Gleichungen (I) oder (II) nach einer der unbekannten Kräfte auf und setzen es in die andere Gleichung ein.

Wir wählen beliebig die Gleichung (I) und lösen diese nach S₃ auf:

$28,98 kN + S_3 \cdot 0,514 + S_4 \cdot 0,949$

$S_3 \cdot 0,514 = -28,98 kN - S_4 \cdot 0,949$

$S_3 = \dfrac{-28,98 kN}{0,514 } - \dfrac{S_4 \cdot 0,949}{0,514 }$

$S_3 = -56,38 kN - S_4 \cdot 1,846$

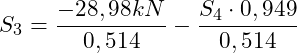
Einsetzen in die Gleichung II für S₃:

$-1,7 kN - [-56,38 kN - S_4 \cdot 1,846] \cdot 0,858 - S_4 \cdot 0,316 = 0$

$-1,7kN + 56,38 kN \cdot 0,858 + S_4 \cdot 1,846 \cdot 0,858 - S_4 \cdot 0,316 = 0$

$-1,7 kN + 48,37 kN + S_4 \cdot 1,584- S_4 \cdot 0,316 = 0$

$46,67 kN + S_4 \cdot 1,584 - S_4 \cdot 0,316 = 0$

Zusammenfassen von S₄:

$46,67 kN + S_4 (1,584 - 0,316) = 0$

$46,67 kN + S_4 \cdot 1,268 = 0$

Und zum Schluss auflösen nach S₄:

$S_4 \cdot 1,268 = -46,67 kN$

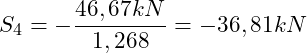$S_4 = -\dfrac{46,67 kN}{1,268} = -36,81 kN$ (Druckstab)

Wir können nun aus einer der beiden Gleichungen (I) oder (II) die Stabkraft S₃ bestimmen:

(I) $28,98 kN + S_3 \cdot 0,514 + S_4 \cdot 0,949$

$S_3 \cdot 0,514 = -28,98 kN - S_4 \cdot 0,949$

$S_3 = \dfrac{-28,98 kN - S_4 \cdot 0,949}{0,514}$

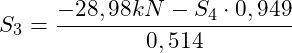
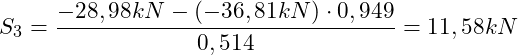$S_3 = \dfrac{-28,98 kN - ( -36,81 kN) \cdot 0,949}{0,514} = 11,58 kN$ (Zugstab)

Diese Berechnung war nun sehr umfangreich. Hier solltest du versuchen systematisch vorzugehen, um keine Fehler zu machen. Sinnvoll ist es bei so großen Gleichungen die Werte soweit wie möglich zusammenzufassen (durch Berechnung des Sinus und Kosinus eines Winkels und Einsetzen bekannter Größen).

Wir gehen nun zum nächsten Knoten über. Es ist nun möglich Knoten III oder Knoten IV zu betrachten. Wir nehmen den Knoten III, weil wir danach nur noch den Knoten VI betrachten müssen und alle Stabkräfte des Fachwerks bestimmt sind. Alternativ können wir auch den Knoten IV und V wählen und sind dann mit unseren Berechnungen fertig.

Knoten III

Zunächst benötigen wir für den Knoten III die Winkel der Stabkräfte S₅ und S₃ zur Waagerechten. Den Winkel von S₃ zur Waagerechten haben wir bereits oben bestimmt mit α₃ = 59,04°.

Wir benötigen demnach den Winkel von der Stabkraft S₅ zur Waagerechten. Dieser ist identisch mit dem Winkel von der Stabkraft S₈ zur Waagerechten, welcher über das große rechtwinklige Dreieck (gestrichelte Linie) bestimmt werden kann:

Trigonometrie, Winkel berechnen, Fachwerk — Knotenpunktverfahren

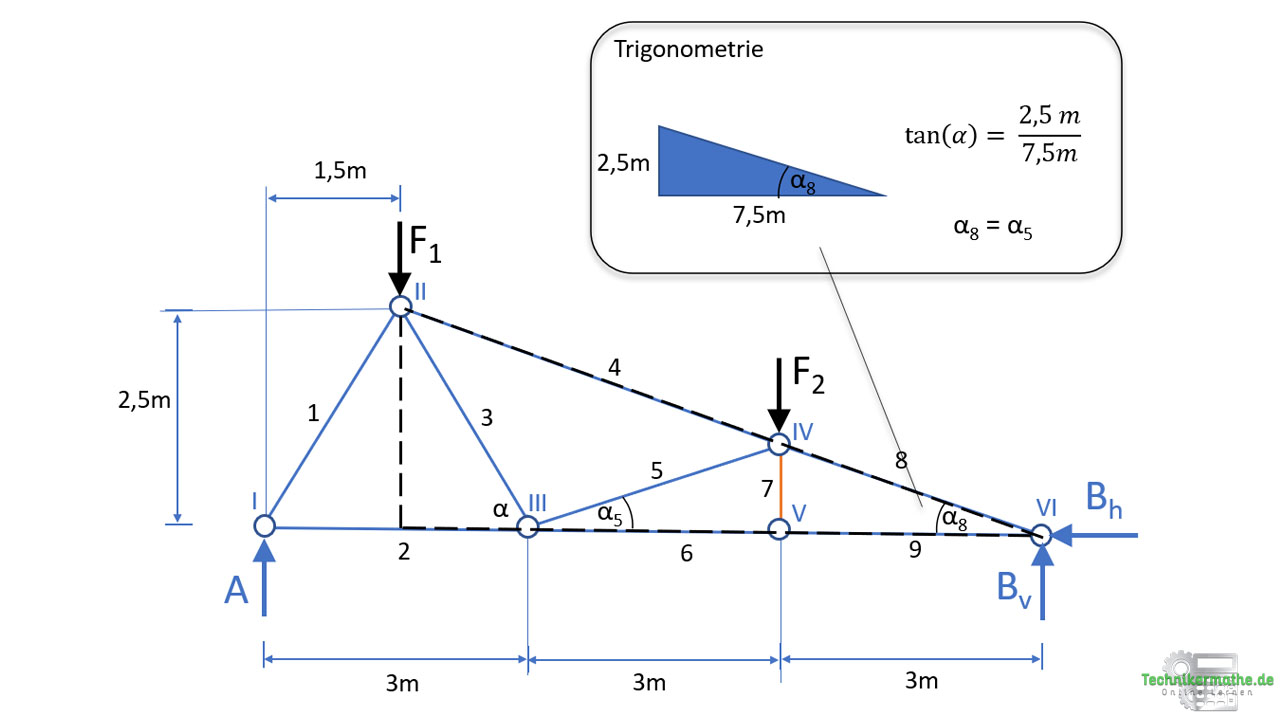
Es gilt:

$\tan(\alpha_8) = \dfrac{2,5m}{7,5m}$

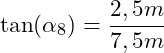
Auflösen nach α₈ ergibt:

$\alpha_8 = \tan^{-1}(\dfrac{2,5m}{7,5m})$

$\alpha_8 = \alpha_5 = 18,43^{\circ}$

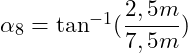
Der Winkel von der Stabkraft S₅ zur Waagerechten ist identisch zu diesem Winkel, weil die Stabkräfte S₅, S₈, S₉ und S₆ ein gleichschenkliges Dreieck formen.

Als nächstes schneiden wir den Knoten III frei:

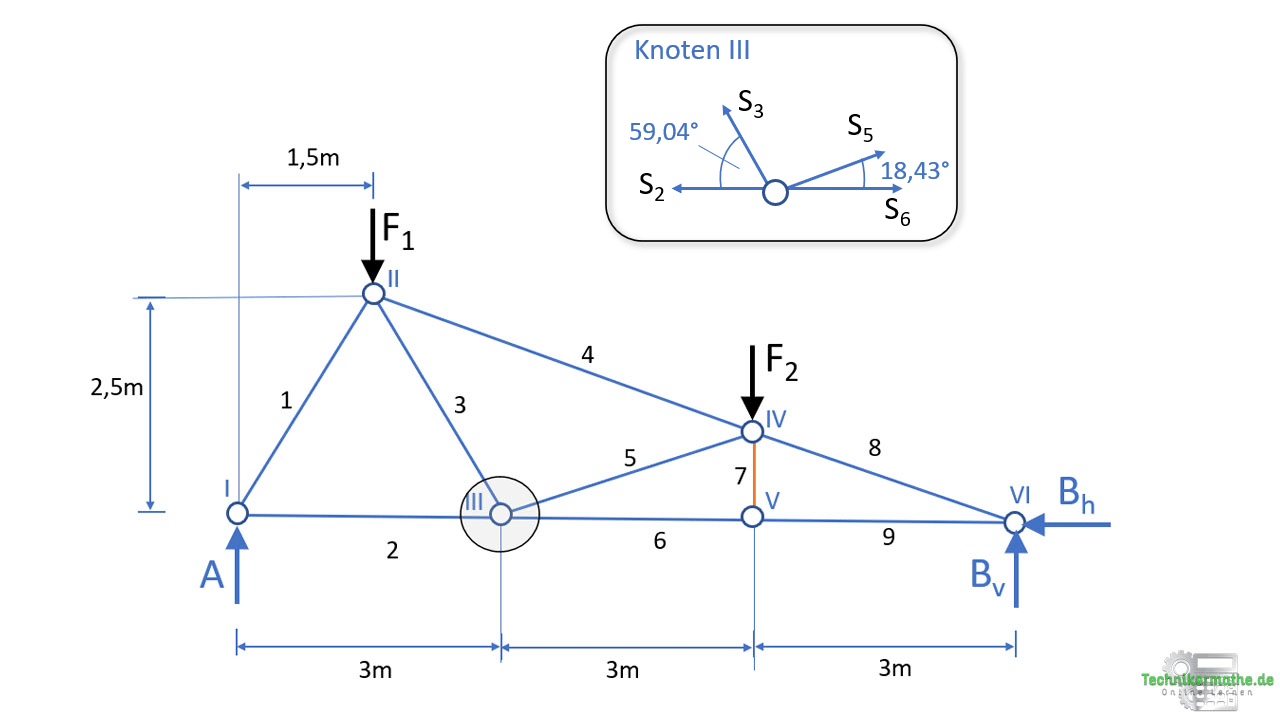
Wir wenden zunächst die Gleichgewichtsbedingung in x-Richtung an:

$\sum F_{ix} = 0: \; \; -S_2 -S_3 \cdot \cos(59,04^{\circ}) + S_5 \cdot \cos(18,43^{\circ}) + S_6 = 0$

Wir setzen die bekannten Werte ein und fassen zusammen (S₂ = 28,95 kN und S₃ = 11,58 kN):

$- 28,95 kN -11,58 kN \cdot \cos(59,04^{\circ}) + S_5 \cdot \cos(18,43^{\circ}) + S_6 = 0$

(I) $-34,91 kN + S_5 \cdot 0,949 + S_6 = 0$

Als nächstes betrachten wir die Gleichgewichtsbedingung in y-Richtung:

$\sum F_{iy} = 0: \; \; S_3 \cdot \sin(59,04^{\circ}) + S_5 \cdot \sin(18,43^{\circ}) = 0$

Auch hier setzen die bekannten Werte ein und fassen zusammen (S₃ = 11,58 kN):

$11,58 kN \cdot \sin(59,04^{\circ}) + S_5 \cdot \sin(18,43^{\circ}) = 0$

(II) $9,93 kN + S_5 \cdot 0,316 = 0$

Aus der Gleichung (II) kann die Stabkraft S₅ berechnet werden:

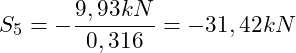$S_5 = -\dfrac{9,93 kN}{0,316} = -31,42 kN$ (Druckstab)

Wir können aus der Gleichung (I) die Stabkraft S₆ ermitteln:

(I) $-34,91 kN + S_5 \cdot 0,949 + S_6 = 0$

$S_6 = 34,91 kN - S_5 \cdot 0,949$

$S_6 = 34,91 kN - (-31,42 kN) \cdot 0,949 = 64,73 kN$ (Zugstab)

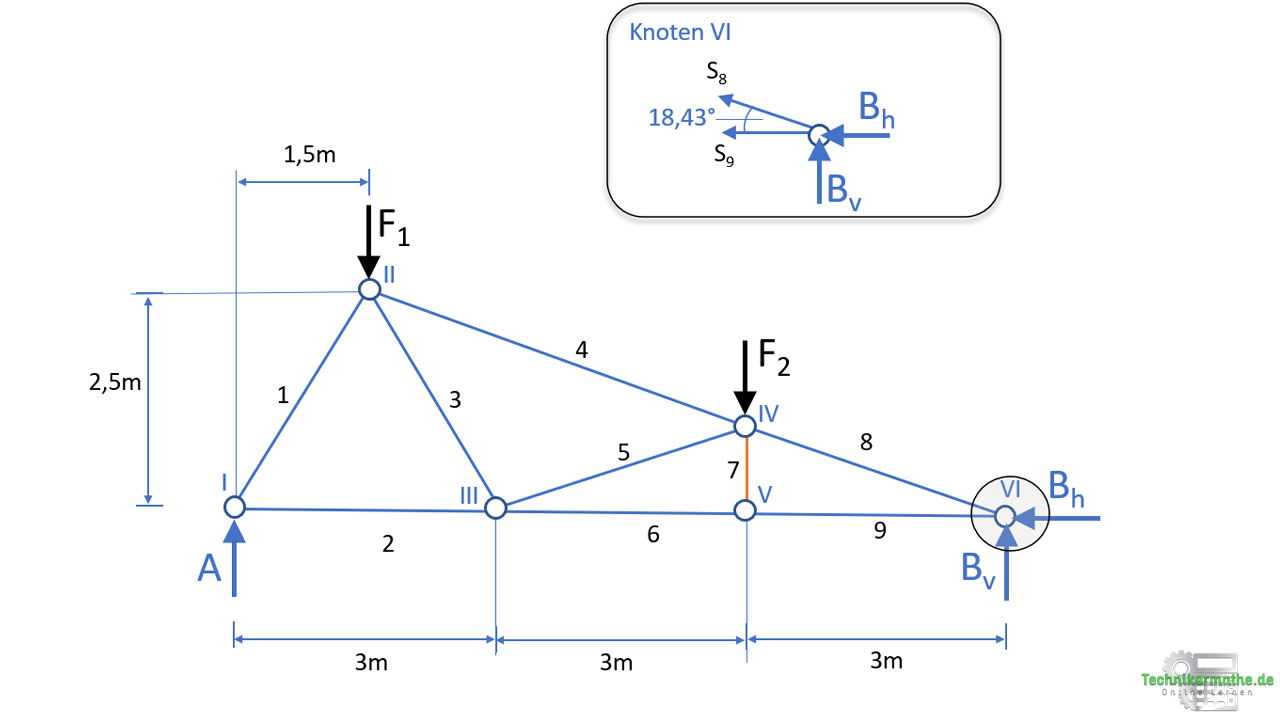
Als nächstes betrachten wir den Knoten VI.

Knoten VI

Hier müssen wir keine weitere Trigonometrie anwenden, um einen Winkel zu bestimmen. Den Winkel von der Stabkraft S8 zur Waagerechten haben wir bereits oben ermittelt mit α₈ = 18,43°.

Wir schneiden den Knoten VI frei:

Zunächst betrachten wir die Gleichgewichtsbedingung in x-Richtung und fassen zusammen:

$\sum F_{ix} = 0: \; \; -S_9 - S_8 \cdot \cos(18,43^{\circ}) - B_H = 0$

(I) $-S_9 - S_8 \cdot 0,949 - B_H = 0$

Danach betrachten wir die Gleichgewichtsbedingung in y-Richtung:

$\sum F_{ix} = 0: \; \; S_8 \cdot \sin(18,43^{\circ}) + B_V = 0$

Einsetzen der bekannten Werte und zusammenfassen (B_V = 21,67 kN):

$S_8 \cdot 0,316 + 21,67 kN = 0$

Auflösen nach S₈:

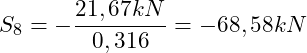$S_8 = -\dfrac{21,67 kN}{0,316} = -68,58 kN$ (Druckstab)

Zur Berechnung der Stabkraft S₉ betrachten wir die Gleichgewichtsbedingung in x-Richtung und setzen S₈ = -68,58 kN und B_h = 0 ein:

(I) $-S_9 - S_8 \cdot 0,949 - B_H = 0$

$-S_9 - (-68,58 kN \cdot 0,949) - 0 = 0$

$-S_9 + 68,58 kN \cdot 0,949 = 0$

$S_9 = 68,58 kN \cdot 0,949 = 65,08 kN$ (Zugstab)

Wir haben alle Stabkräfte im obigen Fachwerks berechnet. Die folgende Tabelle zeigt nochmal die Stabkräfte übersichtlich auf:

Stab	S₁	S₂	S₃	S₄	S₅
Betrag	56,33 kN	28,95 kN	11,58 kN	36,81 kN	31,42 kN
Richtung	Druckstab	Zugstab	Zugstab	Druckstab	Druckstab

Stab	S₆	S₇	S₈	S₉
Betrag	35,78 kN	0	-68,58 kN	65,08 kN
Richtung	Zugstab	Nullstab	Druckstab	Zugstab

Was kommt als Nächstes?

Nachdem du nun weißt, wie das Knotenpunktverfahren anwendet wird, wollen wir uns in der folgenden Lerneinheit das Ritterschnittverfahren anschauen, um unbekannte Stabkräfte eines Fachwerks zu berechnen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++