Das Culmann-Verfahren gehört zu den grafischen Verfahren und wird auch als Vierkräfteverfahren bezeichnet und wurde von dem deutschen Bauingenieur Karl Culmann (1821–1881) entwickelt. Mithilfe des Culmann-Verfahrens können zum Beispiel unbekannte Lagerkräfte bestimmt werden (Richtungen bekannt).
Die äußeren auf den Balken wirkenden Kräfte können zuvor zu einer Resultierenden zusammengefasst werden (Richtung und Größe bekannt). Die Zusammenfassung der äußeren Kräfte zu einer Resultierenden erfolgt mittels grafischer Vektoraddition und Seileckverfahren (vorangegangene Lerneinheiten).
Zur Anwendung des Culmann-Verfahrens werden vier Kräfte benötigt, deren Richtungen bekannt sind. Zusätzlich muss eine Kraft mit ihrer Richtung und ihrem Betrag geben sein.
Dieses Thema ist ein Lernausschnitt aus unserem Onlinekurs: TM1-Statik
- Es müssen drei Kräfte mit ihren Richtungen gegeben sein
- Zusätzlich muss eine weitere Kraft mit ihrer Richtung und ihrem Betrag gegeben sein.
Wir starten zunächst mal mit einem einfachen Beispiel, in welchem wir von einer auf den Balken wirkenden Kraft ausgehen.
Beispiel: Culmann Verfahren – Lagerkräfte bestimmen
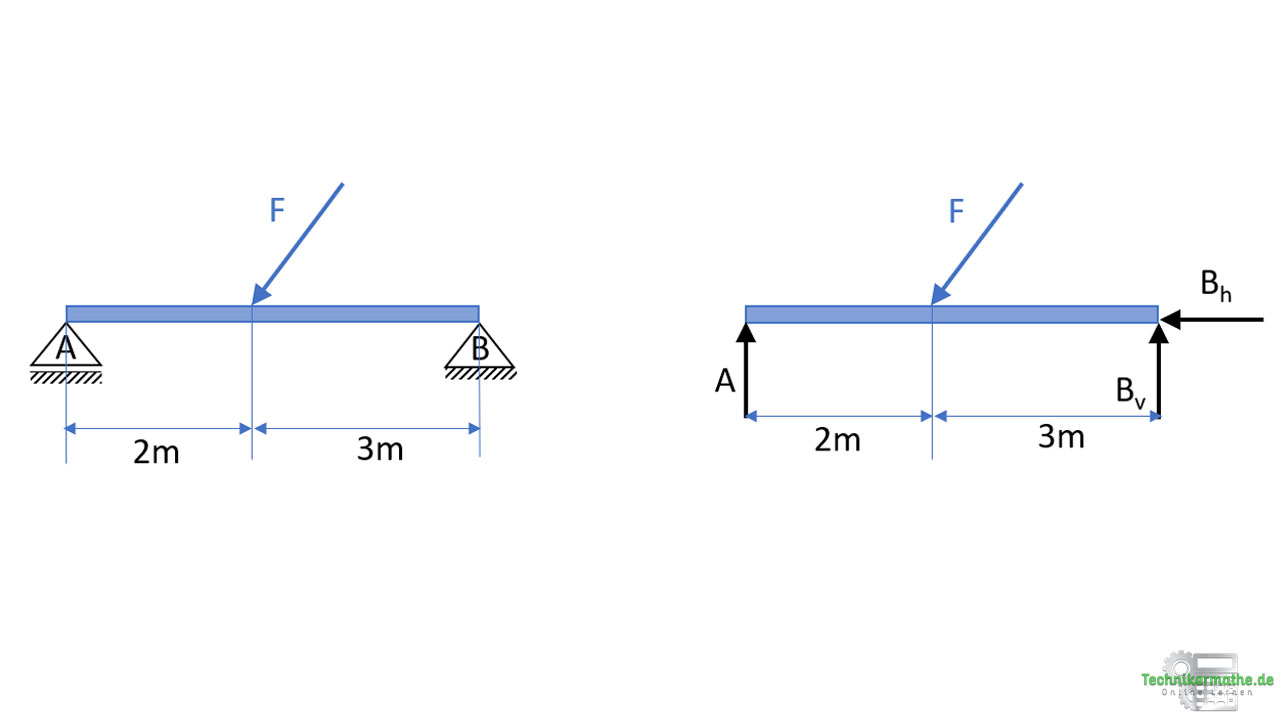
Wir können für dieses Beispiel das Culmann Verfahren anwenden, da drei Lagerkräfte mit ihren Richtungen gegeben sind (Loslager = vertikal, Festlager = vertikal, horizontal) und die äußere Kraft mit Richtung und Betrag gegeben ist.
Schritt 1: Maßstab festlegen
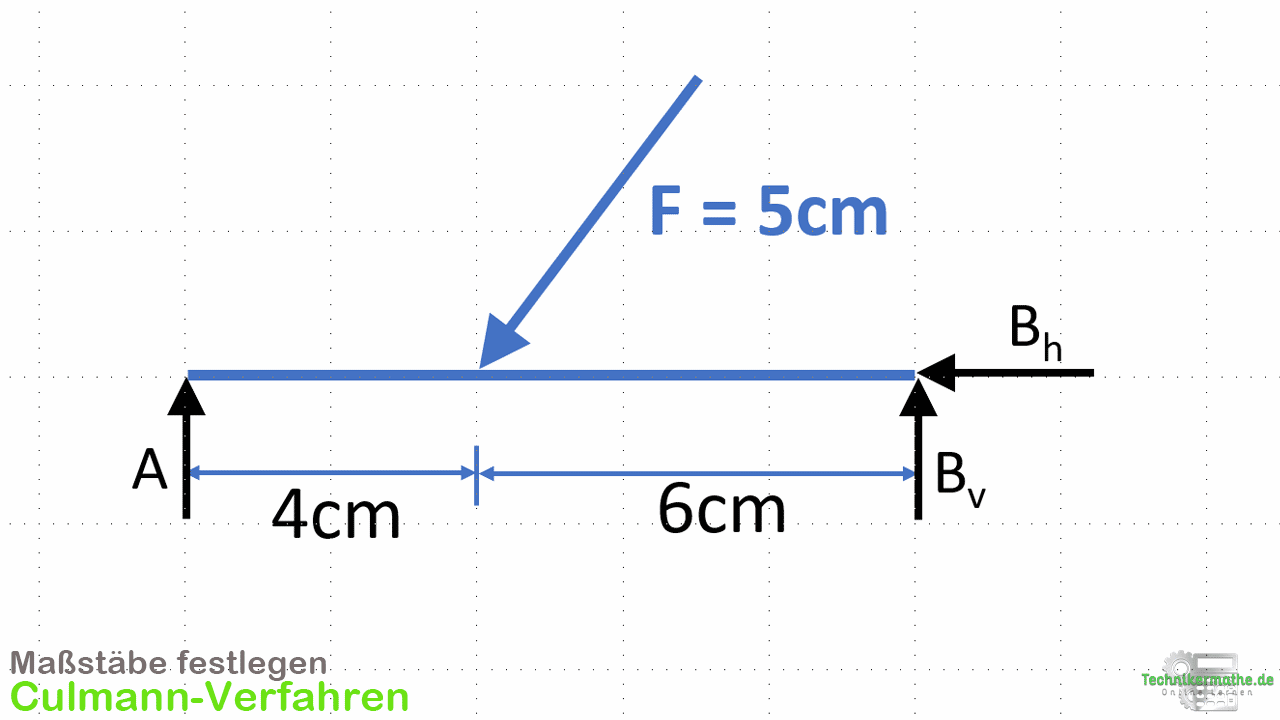
Zunächst müssen wir einen geeigneten Maßstab für die Kräfte festlegen. Die Kraft F ist mit 150 N gegeben. Wir können hier zum Beispiel den Maßstab: 15 N = 0,5cm wählen, so dass wir die Kraft F mit 5 cm einzeichnen können.
Außerdem benötigen wir einen geeigneten Maßstab für die Abmessungen des Balkens. Hier wählen wir den Maßstab:
![]()
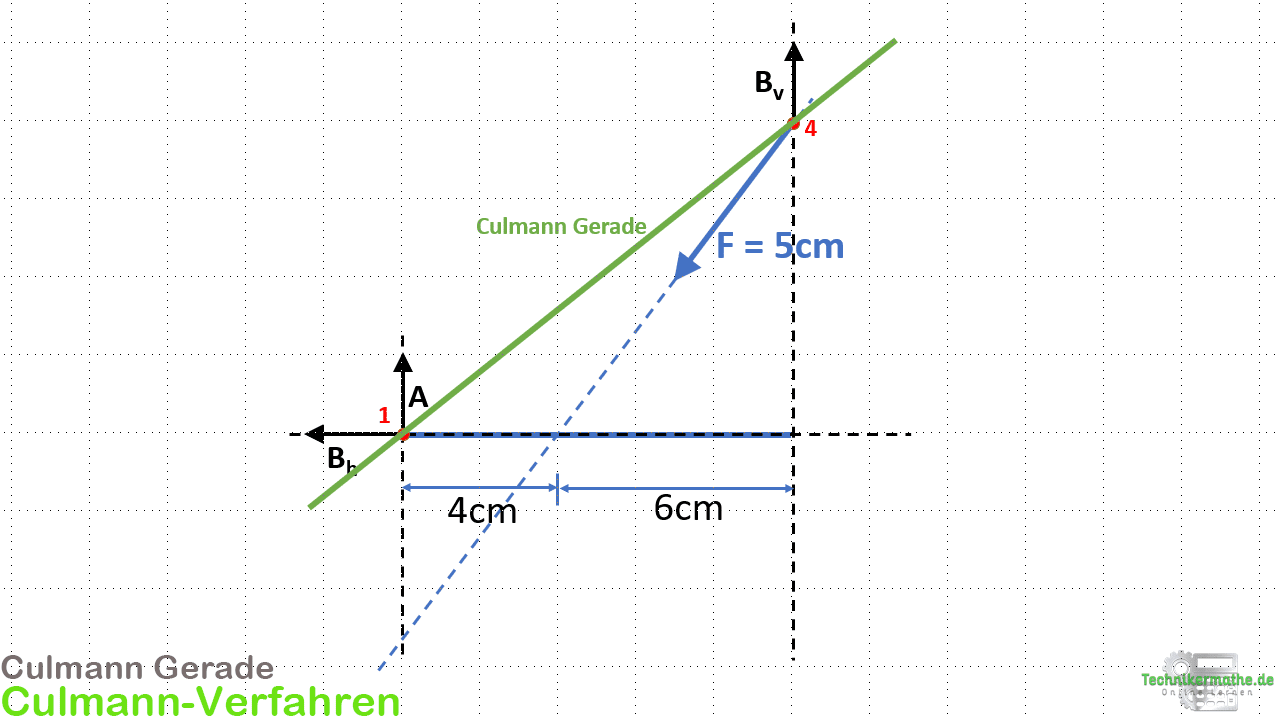
Wir können dann den obigen Balken inklusive Kraft gemäß der gewählten Maßstäbe einzeichnen:
Hinweis: Die Kraft ist übrigens mit einem Winkel von 53° zur Horizontalen gegeben.
Schritt 2: Wirkungslinien verlängern
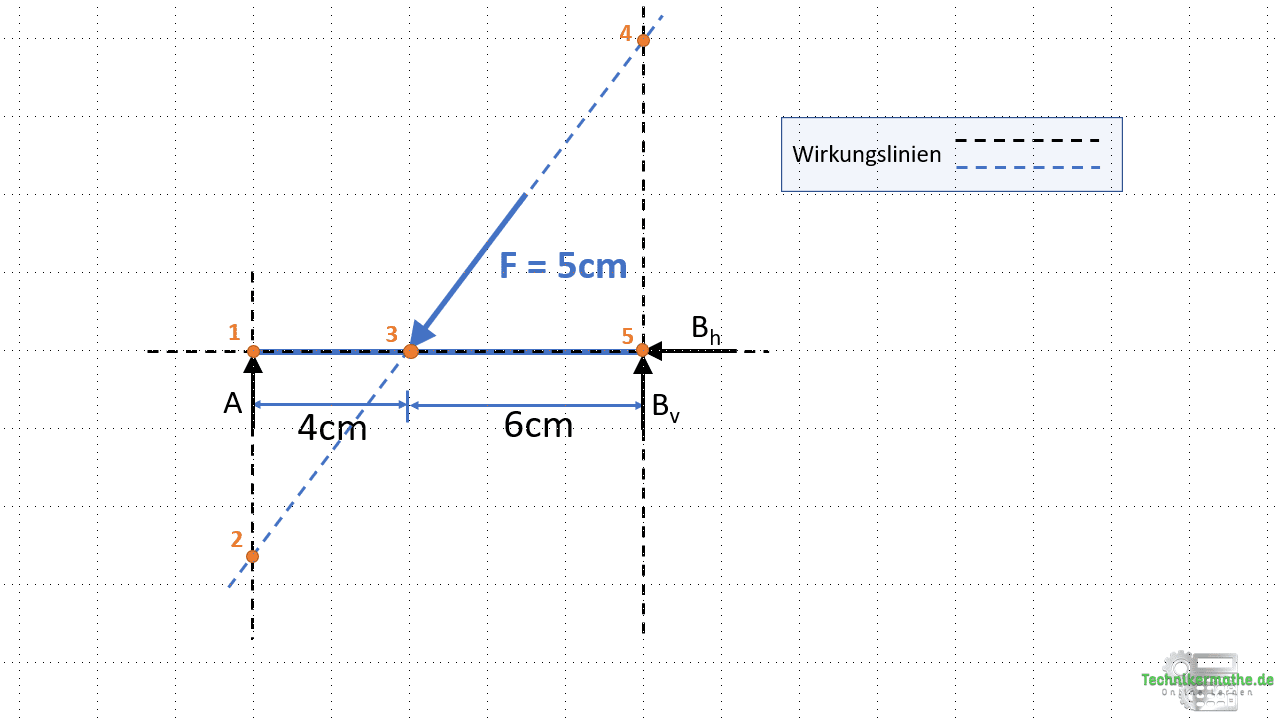
Im nächsten Schritt werden die Wirkungslinien der gegebenen Kräfte so verlängert, dass sich diese schneiden. Es ergeben sich dann 5 Schnittpunkte. Diese Schnittpunkte nummerieren wir beliebig durch:
Schritt 3: Schnittpunkte wählen
Im nächsten Schritt werden nun zwei Schnittpunkte gewählt, in welchen die Kräfte auf ihren Wirkungslinien verschoben werden. Dabei darf jede Kraft insgesamt nur einmal vorkommen. Eine Kraft darf also nicht in zwei oder mehr Schnittpunkten vorkommen.
Betrachten wir die Schnittpunkt 1 und 2. Im Schnittpunkt 1 liegt die Kraft A und die Kraft Bh, im Schnittpunkt 2 die Kraft A und F. Demnach kommt die Kraft A in beiden Schnittpunkten vor. Dies ist nicht möglich.
Wir können die folgenden beiden Konstellationen beliebig wählen:
- Schnittpunkt 1 und 4
- Schnittpunkt 2 und 5
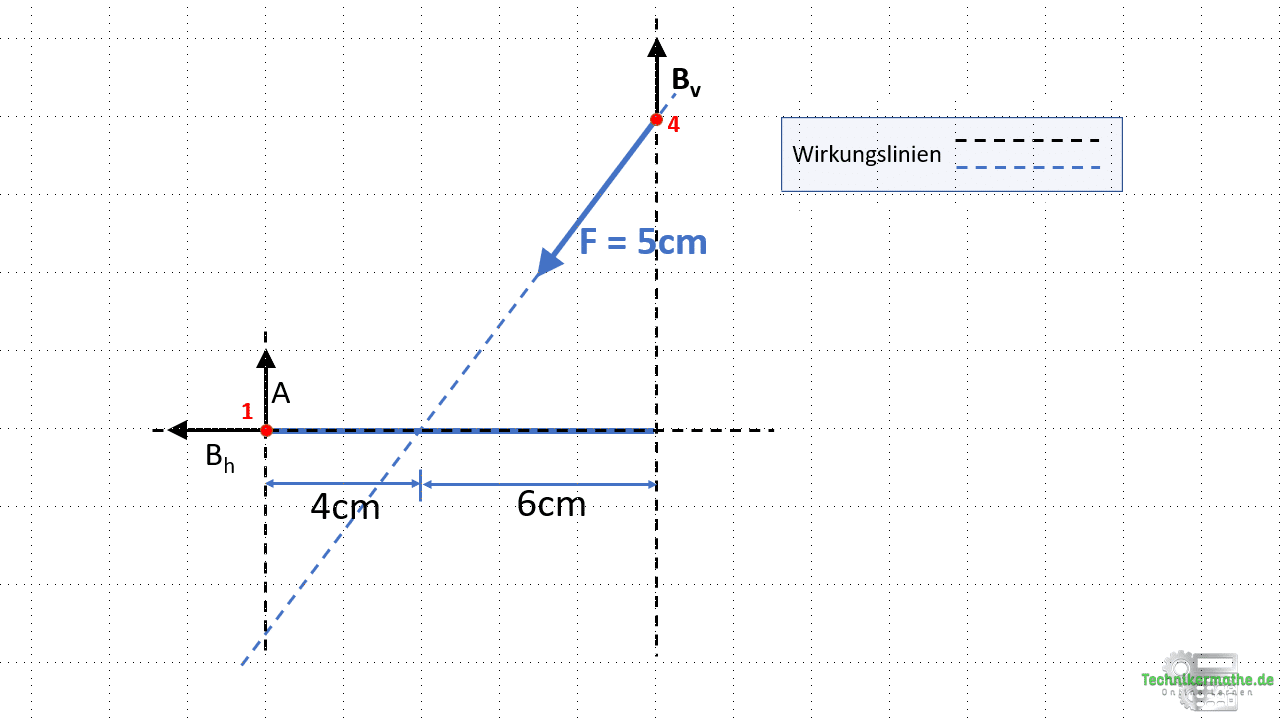
Wir wählen beliebig Schnittpunkt 1 und 4 aus und verschieben die zugehörigen Kräfte auf ihren Wirkungslinien in die Schnittpunkte:
Schritt 4: Culmann Gerade einzeichnen
Im nächsten Schritt können wir die Culmann Gerade einzeichnen, indem wir die beiden gewählten Schnittpunkte 1 und 4 miteinander verbinden:
Schritt 5: Kraftplan zeichnen – Lagerkräfte bestimmen
Die Culmann-Gerade gibt nichts anderes an, als die Richtung der Resultierenden aus den Kräften Bv und F und der Richtung der Resultierenden aus den Kräfte A und Bh (siehe folgende Grafiken).
Resultierende R1
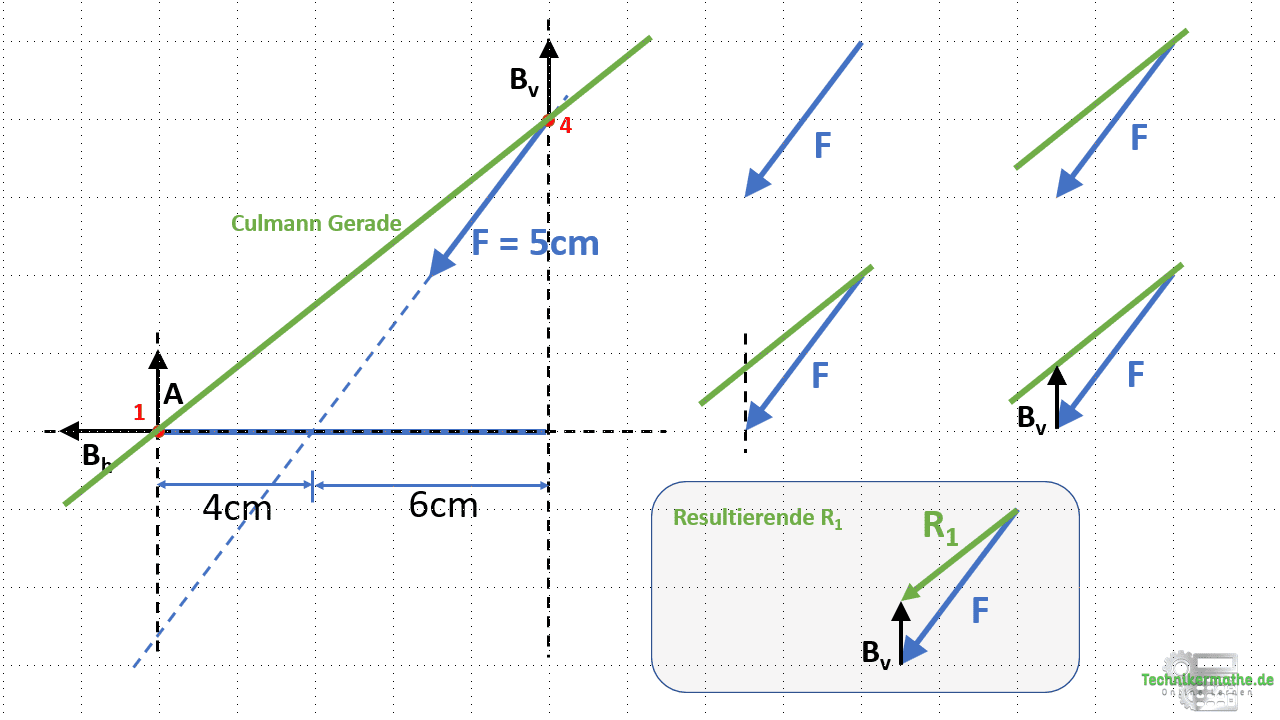
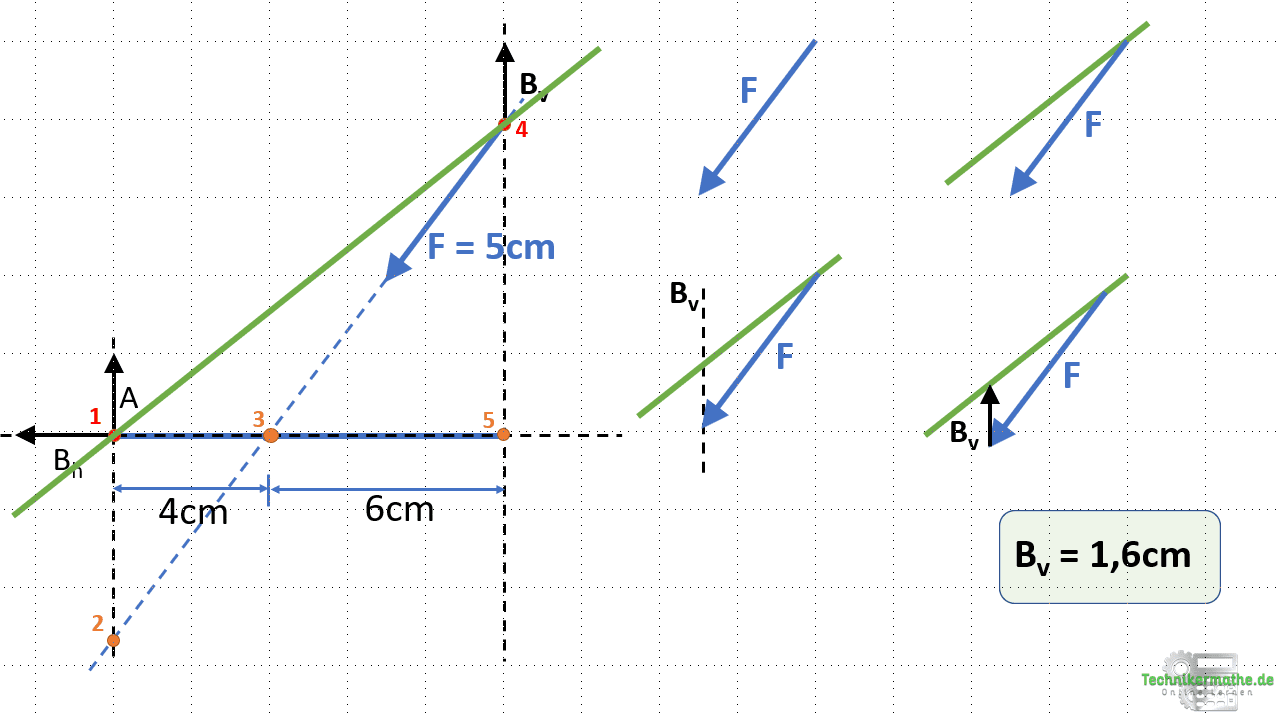
Wir beginnen nun damit den Kraftplan zu zeichnen. Dazu beginnen wir mit derjenigen Kraft, für welche Richtung und Größe bekannt ist (hier: Kraft F). Die Kraft F wird mit ihrer Richtung (53° zur Horizontalen) und ihrer Größe (5 cm) auf ein Zeichenblatt gezeichnet. Die Kraft F liegt gemeinsam mit der Kraft Bv im Schnittpunkt 4. Wir zeichnen nun die bekannte Kraft F ein, die Culmann Gerade und zum Schluss die Kraft Bv:
Die Kraft F liegt im Schnittpunkt 4, in welcher auch die Kraft Bv liegt. Wir können als erstes die Kraft Bv wie folgt bestimmen:
- Nachdem wir die Kraft F mit Richtung und Größe eingezeichnet haben, legen wir die Culmann Gerade an den Anfangspunkt der Kraft F. Danach legen wir die Wirkungslinie der Kraft Bv an die Spitze der Kraft F.
- Die Kraft Bv liegt zwischen Spitze der Kraft F und der Culmann Geraden. Da wir Kräfte grafisch so zusammenfügen, dass Anfangspunkt einer Kraft die Spitze der vorangegangenen Kraft berührt, zeigt die Lagerkraft Bv nach oben.
Zur Bestimmung einer Resultierenden, wird eine grafische Vektoraddition durchgeführt. Dabei wird eine Kraft eingezeichnet und die nachfolgenden Kräfte mit ihrem Anfangspunkt an die Spitze der Vorgängerkraft gelegt. Die Resultierende wird dann eingezeichnet, indem der Anfangspunkt an den Anfangspunkt der zuerst gewählten Kraft und die Spitze der Resultierenden an die Spitze der zuletzt gewählten Kraft gelegt wird.
Für unseren Fall ist die Kraft F die erste Kraft und die Kraft Bv die letzte Kraft. Damit zeigt die Resultierende R1 nach links unten.
Nach dem Messen der Kraft Bv (Länge des Pfeils) erhalten wir die Länge Bv = 1,6 cm. Dies entspricht einem Betrag von Bv = 48 N. Wir können nun auch noch die Resultierende R1 abmessen, die eine Länge von ca. 3,8 cm aufweist. Damit ist R1 ≈ 114 N.
Resultierende R2
Die Resultierende R2 der beiden Kräfte A und Bh ist genau so groß wie die Resultierende R1, zeigt in dieselbe Richtung (also in Richtung der Culmann-Geraden) und ist genau entgegengesetzt zu R1 gerichtet:
![]()
R2 ist genau entgegengesetzt zu R1 gerichtet und liegt auf der Culmann Geraden.
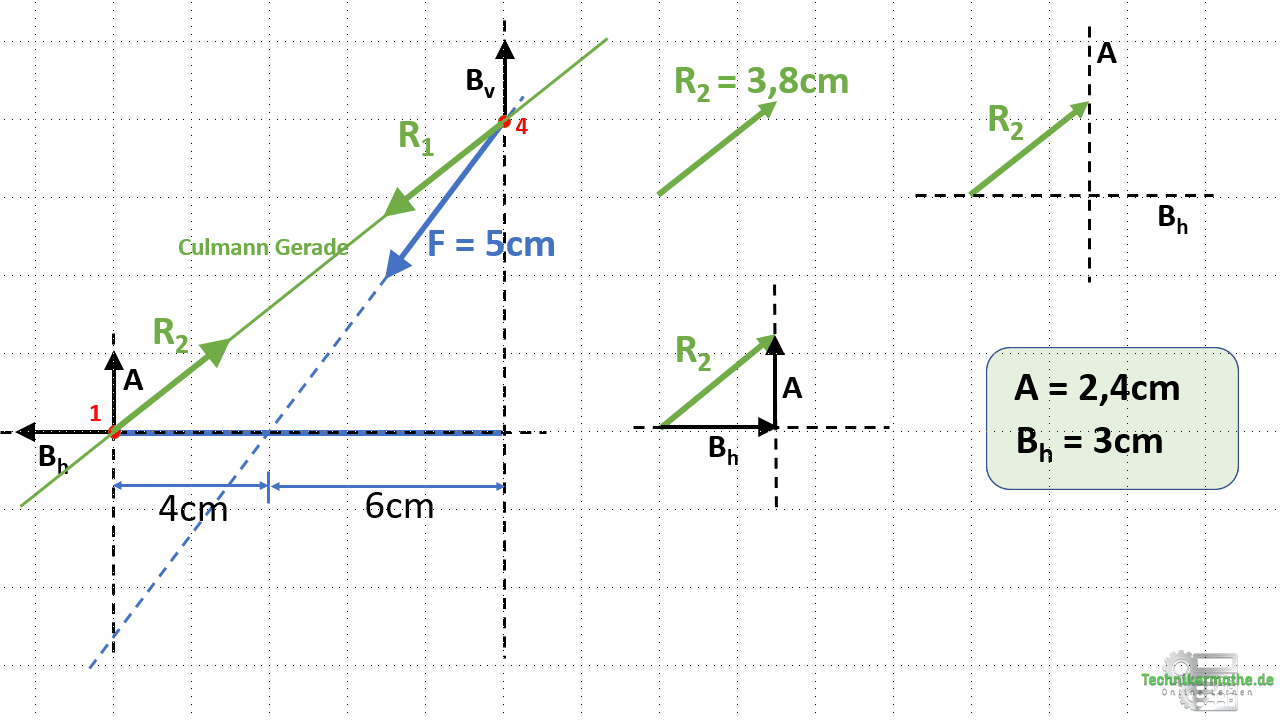
Wir können mit dieser Kenntnis den zweiten Kraftplan einzeichnen. Dazu zeichnen wir zunächst die uns von der Richtung und der Größe bekannte Resultierende Kraft R2 ein. Danach legen wir die Wirkungslinien von Bh und A so an die Resultierenden, dass eine Wirkungslinie die Resultierende an ihrem Anfangspunkt und eine Wirkungslinie die Resultierenden an ihrer Spitze berührt. Die beiden Wirkungslinien müssen sich zusätzlich schneiden:
In der obigen Grafik haben wir die Wirkungslinien von Bh an den Anfangspunkt der Resultierenden R2 gelegt und die Wirkungslinie von A an die Spitze der Resultierenden. Die beiden Wirkungslinien schneiden sich zudem.
Zur Bestimmung einer Resultierenden, wird eine grafische Vektoraddition durchgeführt. Dabei wird eine Kraft eingezeichnet und die nachfolgenden Kräfte mit ihrem Anfangspunkt an die Spitze der Vorgängerkraft gelegt. Die Resultierende wird dann eingezeichnet, indem der Anfangspunkt an den Anfangspunkt der zuerst gewählten Kraft und die Spitze der Resultierenden an die Spitze der zuletzt gewählten Kraft gelegt wird.
Für unseren Fall muss also Bh die erste Kraft darstellen und A die letzte Kraft. Damit können wir die Pfeile der beiden Kräfte einzeichnen und anschließend die Längen abmessen.
Nach dem Abmessen der Längen ergibt sich:
![]()
![]()
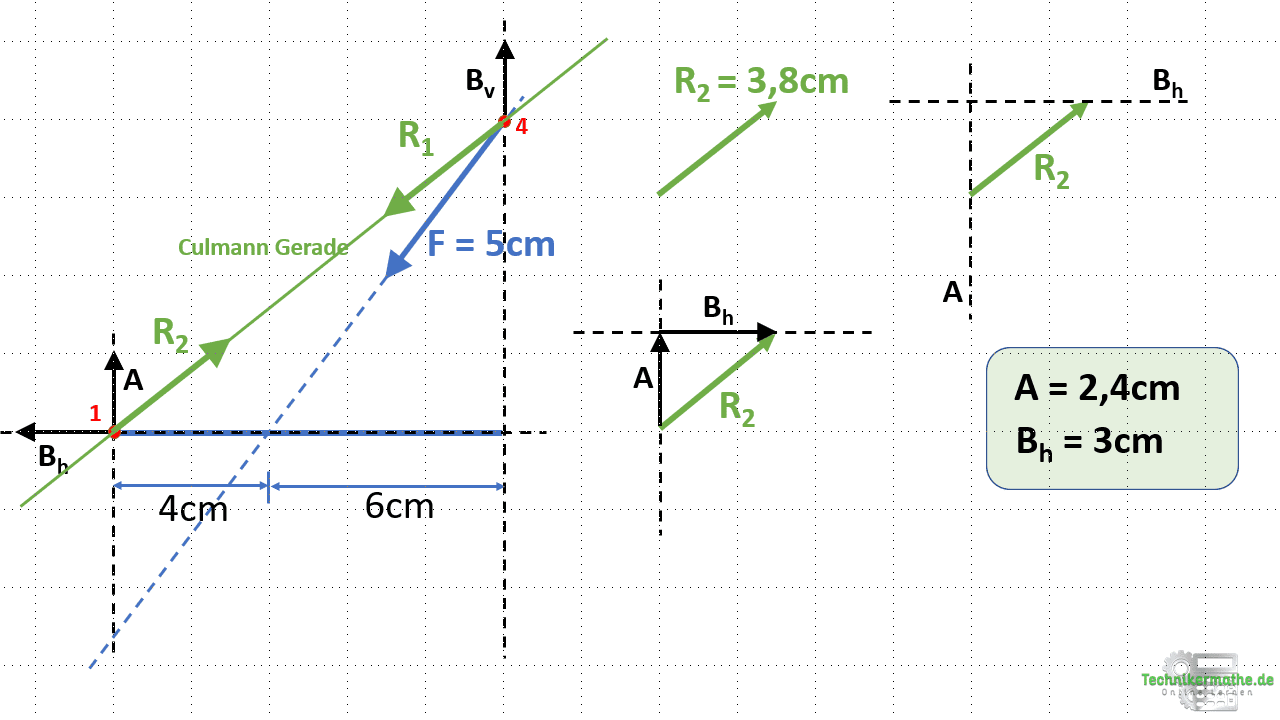
Wir können natürlich ebenfalls die beiden Kräfte genau anders herum anordnen:
In der obigen Grafik haben wir die Wirkungslinien von A an den Anfangspunkt der Resultierenden R2 gelegt und die Wirkungslinie von Bh an die Spitze der Resultierenden. Die beiden Wirkungslinien schneiden sich zudem.
In diesem Fall muss also A die erste Kraft darstellen und Bh die letzte Kraft. Damit können wir die Pfeile der beiden Kräfte einzeichnen und anschließend die Längen abmessen. Es ergeben sich natürlich dieselben Längen wie bereits oben gezeigt.
Variante ohne Resultierende
Die obige Vorgehensweise sollte aufzeigen, dass die Culmann Gerade die Richtung der Resultierenden der Kräftepaare darstellt. Es gibt noch eine weitere Möglichkeit das Culmann-Verfahren anzuwenden. Diese erfolgt ohne Anwendung der Resultierenden.
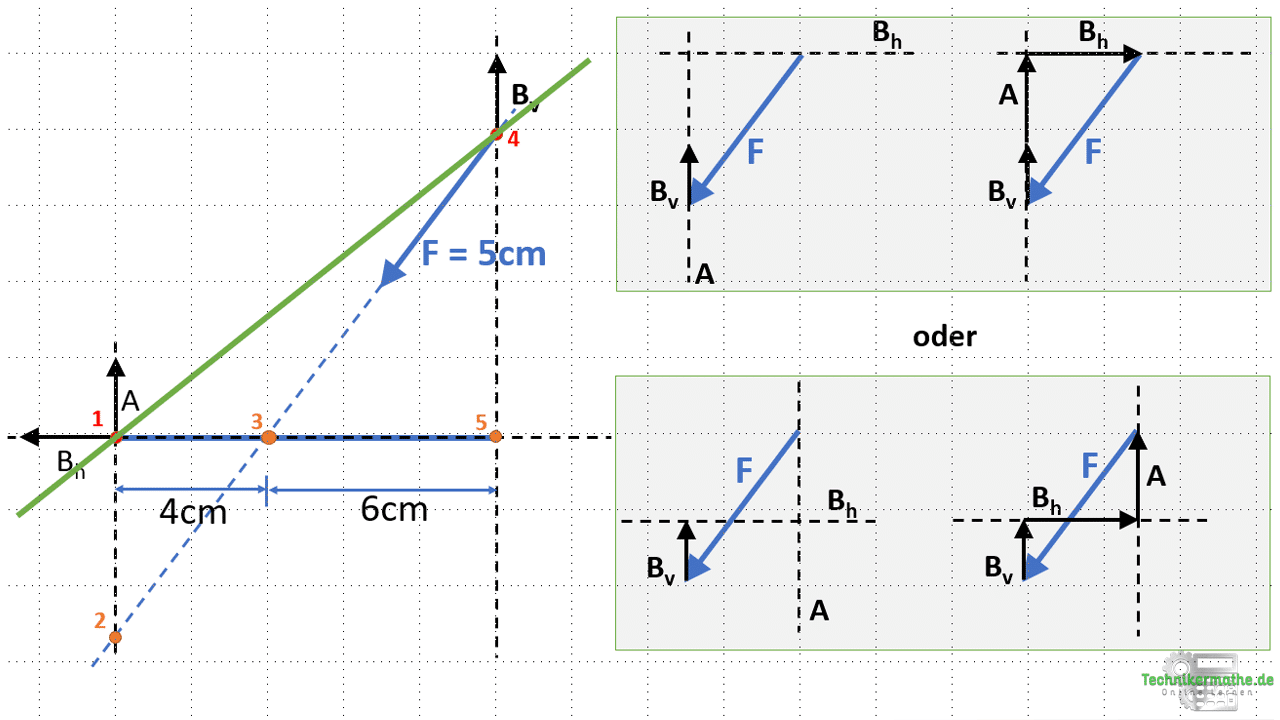
Auch hier stellen wir den Kraftplan zunächst für den Schnittpunkt mit der bekannten äußeren Kraft F auf, fügen die Culmann-Gerade an und zeichnen die Wirkungslinie der Kraft Bv ein:
Dieses Vorgehen ist identisch mit dem obigen Vorgehen (Überschrift Resultierende R1). Wir messen nun aber nicht die Resultierende R1, sondern legen direkt die Kräfte aus dem zweiten Schnittpunkt an:
- Eine der beiden Kräfte A oder Bh wird mit ihrer Wirkungslinien an die Spitze der Kraft Bv gelegt.
- Die andere Kraft wird mit ihrer Wirkungslinie an den Anfangspunkt der Kraft F gelegt.
Welche Kraft für die I. und welche für II. verwenden, ist beliebig wählbar.
Oben in der Grafik siehst du beide Varianten eingezeichnet. Einmal haben wir die Kraft A mit ihrer Wirkungslinie an die Spitze der Kraft Bv gelegt und die Kraft Bh mit ihrer Wirkungslinie an den Anfangspunkt der Kraft F (oben) und einmal genau umgekehrt (unten). Beides führt zum selben Ergebnis.
Wir reihen die Kräfte gemäß grafischer Vektoraddition aneinander, so dass der Anfangspunkt einer Kraft die Spitze der Vorgängerkraft berührt und erhalten damit die oben angegebenen Richtungen.
Wichtig: Hier gibt es nach Aneinanderreihung aller Kräfte keine Resultierende, weil wir alle äußeren Kräfte betrachten. Da sich das System in Ruhe und damit im Gleichgewicht befindet, muss die Summe aller Kräfte gleich Null ergeben. Für die grafische Vektoraddition gilt dann, dass sich ein geschlossenes Krafteck ergibt.
Nach Messen der Kräfte Bv, Bh und A erhalten wir:
![]()
![]()
![]()
Damit ergibt sich nach Umrechnung gemäß 15 N = 0,5 cm:
![]()
![]()
![]()
Das Culmann Verfahren endet hier, da alle unbekannten Auflagerkräfte bestimmt sind.
Es ist unbedingt zu beachten, dass du die Abmessungen des Körpers mit berücksichtigst. Für die Abmessungen des Körpers sowie für die Kräfte müssen Maßstäbe so gewählt werden, dass du diese gut auf ein Zeichenpapier übertragen kannst.
Sind in der Aufgabe mehrere äußere Kräfte gegeben, so musst du diese zunächst zu einer Resultierenden zusammenfassen. Diese kannst du mittels grafischer Vektoraddition (Betrag und Richtung) und Seileckverfahren (Lage der Resultierenden) ermitteln. Danach kannst du das Culmann-Verfahren anwenden.
Die Auswahl der Schnittpunkte (Schritt 3) sollte so vorgenommen werden, dass die beiden gewählten Schnittpunkte weit genug auseinander liegen, da ansonsten die Culmann Gerade sehr klein und damit der Kraftplan ungenau wird. Alternativ kannst du den Maßstab vergrößern.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team