TM1 – Schnittgrößenverläufe bei Dreieckslast

Schnittgrößen sind die internen Kräfte und Momente, die entlang eines Balkens auftreten, wenn er einer Belastung ausgesetzt ist. Diese Belastungen können beispielsweise durch Kräfte, Momente oder Temperaturänderungen verursacht werden. Die wichtigsten Schnittgrößen sind:

Normalkraft (Axialkraft): Die Normalkraft ist die Kraft, die parallel zur Längsachse des Balkens wirkt. Sie entsteht, wenn der Balken einer Zug- oder Druckbelastung ausgesetzt ist.

Querkraft (Schubkraft): Die Querkraft ist die Kraft, die senkrecht zur Längsachse des Balkens wirkt. Sie entsteht, wenn der Balken einer seitlichen Belastung ausgesetzt ist.

Biegemoment: Das Biegemoment ist das Moment, das um die Querachse des Balkens wirkt. Es entsteht, wenn der Balken einer Biegebelastung ausgesetzt ist, die dazu führt, dass der Balken sich biegt.

Diese Schnittgrößen sind entscheidend für das Verständnis des Verhaltens eines Balkens unter Belastung und spielen eine wichtige Rolle bei der Berechnung seiner Tragfähigkeit und Dimensionierung für bestimmte Anwendungen.

In dieser Lerneinheit wollen wir uns anschauen, wie die Schnittgrößenverläufe grafisch eingezeichnet werden, wenn eine Dreieckslast auf den Balken wirkt.

Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.

Dieses Thema ist ein Auszug aus unserem Onlinekurs TM1-Statik.

In dieser Lerneinheit wollen wir uns anschauen, wie die Schnittgrößenverläufe grafisch eingezeichnet werden, wenn eine Dreieckslast auf den Balken wirkt. Wir behandeln:

Den Normalkraftverlauf.
Den Querkraftverlauf sowie die Bestimmung von Minimum/Maximum und die Stelle des Nulldurchgangs.
Den Momentenverlauf sowie die Bestimmung von Minimum/Maximum.

Beispiel: Balken mit zwei Dreieckslasten

Dazu betrachten wir das vorangegangene Beispiel mit den zwei gegebenen Dreieckslasten:

Schnittgrößenverläufe: Dreieckslasten auf Balken, Nachhilfe Techniker — Dreieckslast: Beispiel

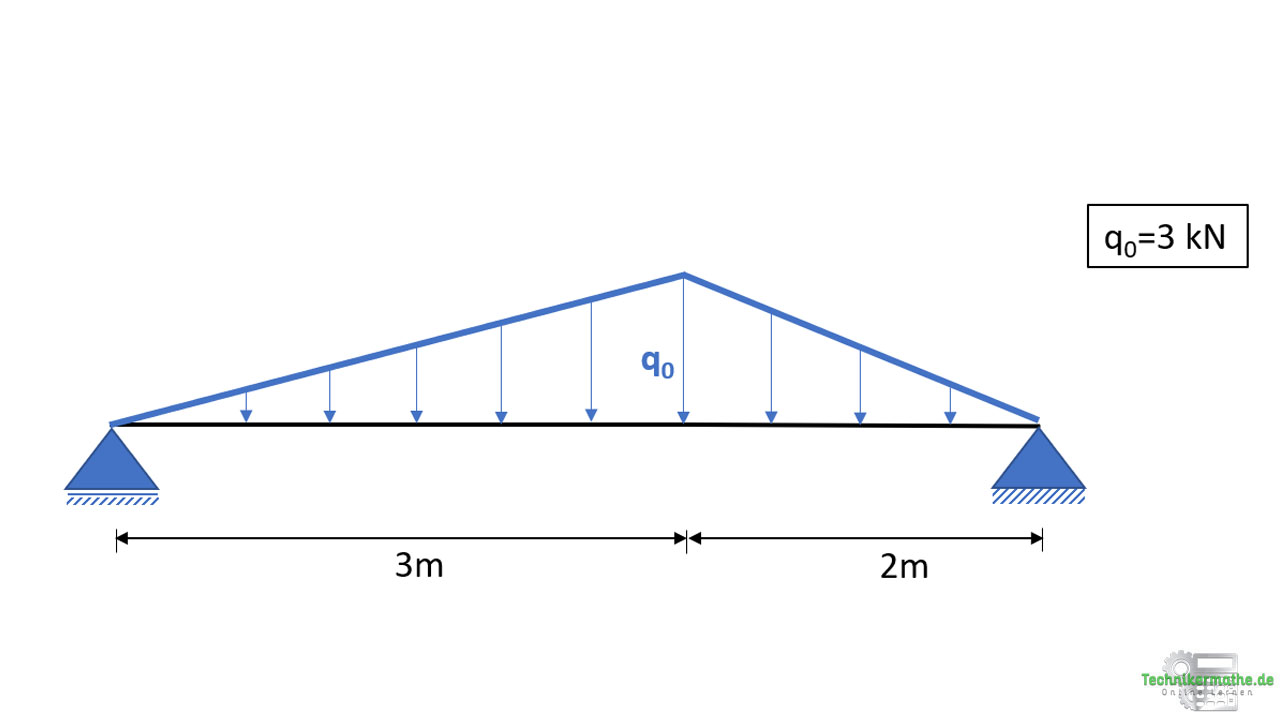
Für den obigen Balken mit den zwei Dreieckslasten haben wir die folgenden Schnittgrößenverläufe in der vorangegangenen Lerneinheit berechnet:

	Schnitt 1	Schnitt 2
Normalkraftverlauf	$N_1 = 0$	$N_2 = 0$
Querkraftverlauf	$Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2$	$Q_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-x)^2 - 4 kN$
Momentenverlauf	$M_1 = 3,5 kN \cdot x - \dfrac{1}{6} \frac{kN}{m^2}\cdot x^3$	$M_2 = 4 kN \cdot (5m - x) - \dfrac{1}{4} \frac{kN}{m^2}\cdot (5m-x)^3$

Schnittgrößenverläufe: Normalkraftverlauf

Der Normalkraftverlauf ist im gesamten Balken Null, da keine horizontalen Kräfte an den Balken angreifen.

Normalkraftverlauf bei Dreieckslast, Schnittgrößenverläufe, Prüfungsvorbereitung Techniker, Normalkraftverlauf, Schnittgrößen, Streckenlast — Normalkraftverlauf bei Dreieckslasten

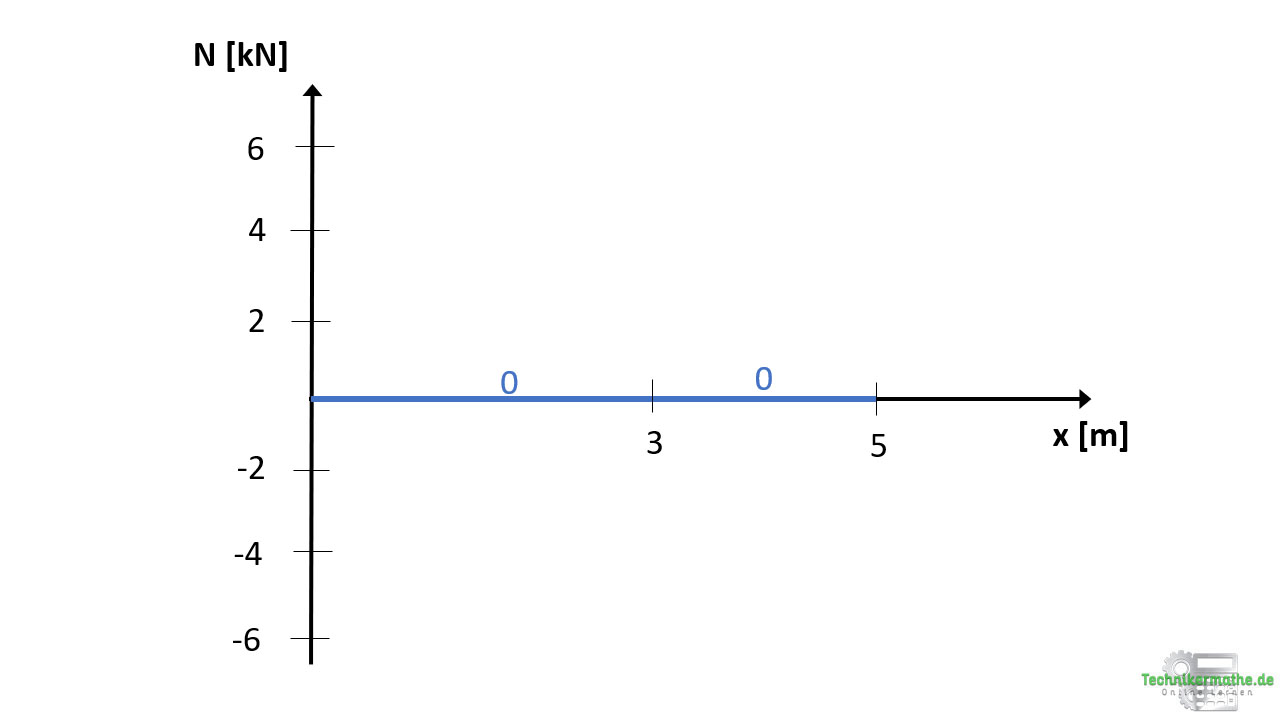
Der Normalkraftverlauf ist unabhängig von der gegebenen Dreieckslast, weil es sich bei dieser um eine Vertikallast handelt (senkrecht zur Balkenachse). Es tritt nur dann ein Normalkraftverlauf auf, wenn auch äußere Normalkräfte (Kräfte in Richtung der Balkenachsen) auf den Balken wirken.

Schnittgrößenverläufe: Querkraftverlauf

Der Querkraftverlauf ist in beiden Schnittbereich quadratisch. Es ergibt sich also für beide Schnittbereiche eine quadratische Parabel:

Querkraftverlauf bei Dreieckslasten, Nachhilfe Techniker, Querkraftverlauf, Dreieckslast, Streckenlast, Schnittgrößenverläufe — Schnittgrößenverläufe: Querkraftverlauf bei Dreieckslasten

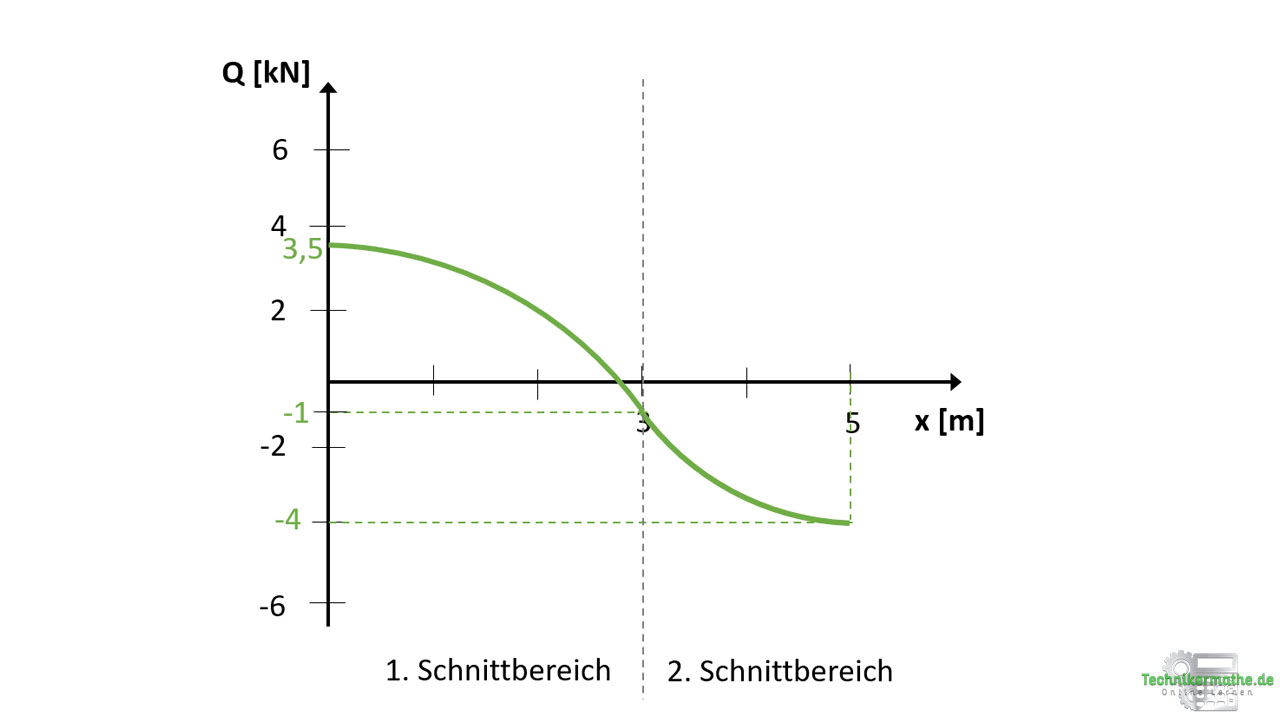
Schauen wir uns im Folgenden mal genauer an, wie der obige Querkraftverlauf eingezeichnet wird.

Querkraftverlauf im ersten Schnittbereich

Im ersten Schnittbereich ist der parabelförmige Verlauf wie folgt gegeben:

$Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2$

Als erstes wollen wir den Beginn und das Ende des Querkraftverlaufs berechnen. Dazu setzen wir x = 0m (Beginn der Streckenlast) und x = 3m (Ende der Streckenlast) in die Gleichung Q₁ ein:

$x = 0m: \; Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot (0m)^2 = 3,5 kN$

$x = 3m: \; Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot (3m)^2 = -1 kN$

Diese Streckenlast beginnt demnach bei Q = 3,5 kN und endet bei Q= -1 kN. Der Querkraftverlauf im ersten Schnittbereich muss durch die x-Achse verlaufen (Nulldurchgang), weil der Verlauf bei 3,5 kN (positiv) beginnt und bei -1 kN (negativ endet).

Nulldurchgang des Querkraftverlaufs bestimmen

Durch Nullsetzen des Querkraftverlaufs und anschließendes Auflösen nach x können wir die Stelle des Nulldurchgangs berechnen:

$Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2 = 0$

Wir haben eine quadratische Funktion gegeben, die wir zunächst in die allgemeine Form bringen:

$y = ax^2 + bx + c$

Stellen wir nun den gegebenen Querkraftverlauf so um, dass die obige Form gegeben ist, so erhalten wir:

$Q_1 = - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2 + 3,5 kN$

Damit ist

a = -0,5, b = 0 und c = 3,5.

Zur Bestimmung der Nullstellen der quadratischen Funktion können wir zum Beispiel die Mitternachtsformel anwenden:

$x_{1,2} = \dfrac{-b \pm \sqrt{b^2-4ac}}{2a}$

Wir haben oben bestimmt, dass a = -0,5, b = 0 und c = 3,5 ist. Wir betrachten nun den Querkraftverlauf ohne Einheiten (zur besseren Übersicht):

$Q_1 = - \dfrac{1}{2} \cdot x^2 + 3,5$

Einsetzen von a, b und c ergibt dann:

$x_{1,2} = \dfrac{- 0 \pm \sqrt{0^2 - 4 \cdot (-0,5) \cdot 3,5}}{2 \cdot (-0,5)}$

$x_{1} = \dfrac{+ \sqrt{0^2- 4 \cdot (-0,5) \cdot 3,5}}{2 \cdot (-0,5)} = -2,65$

$x_{2} = \dfrac{ - \sqrt{0^2-4 \cdot (-0,5) \cdot 3,5}}{2 \cdot (-0,5)} = 2,65$

Da hier kein negativer Wert möglich ist (wir bewegen uns vom Balkenanfang nach rechts in positive x-Richtung), muss der Nulldurchgang bei x = 2,65 Meter gegeben sein.

Maximum/Minimum bestimmen

Wir wollen nun noch herausfinden, ob die Parabel eine Extremwert aufweist und an welcher Stelle.

Wiederholung!

Zunächst wird die Stelle (der x-Wert) des Extremums bestimmt, indem die 1. Ableitung gebildet, diese gleich Null gesetzt und nach x-aufgelöst wird.
Danach wird die 2. Ableitung gebildet. Ist diese noch abhängig von x, wird der in 1. bestimmte x-Wert dort eingesetzt.
Ist die 2. Ableitung größer Null, dann liegt ein Minimum vor.
Ist die 2. Ableitung kleiner Null, dann liegt ein Maximum vor.
Einsetzen des in 1. bestimmten x-Werts in die Ausgangsfunktion, um die Größe des Maximums/Minimums zu bestimmen.

Wir bilden nun zunächst die 1. Ableitung, setze diese gleich Null und lösen nach x auf:

$Q_1' = -x$

$0 = -x$

$x = 0$

Es ergibt sich sofort, dass x = 0 ist, und damit eine Extremstelle bei x = 0 gegeben ist. Wir wollen noch herausfinden, ob ein Minimum oder Maximum gegeben ist, dazu bilden wir die 2. Ableitung:

$Q_1'' = -1$ Maximum

Hierbei handelt es sich um ein Maximum an der Stelle x = 0. Da die Stelle x = 0 auf gleichzeitig der Beginn des Querkraftverlaufs ist, besitzt das Maximum dieselbe Höhe wie der Startwert:

$Q_1 = - \dfrac{1}{2} \cdot (0m)^2 + 3,5 = 3,5$

Es muss sich hier um eine nach unten geöffnete fallende Parabel handeln, da eine Parabel nach einem Maximum abfällt.

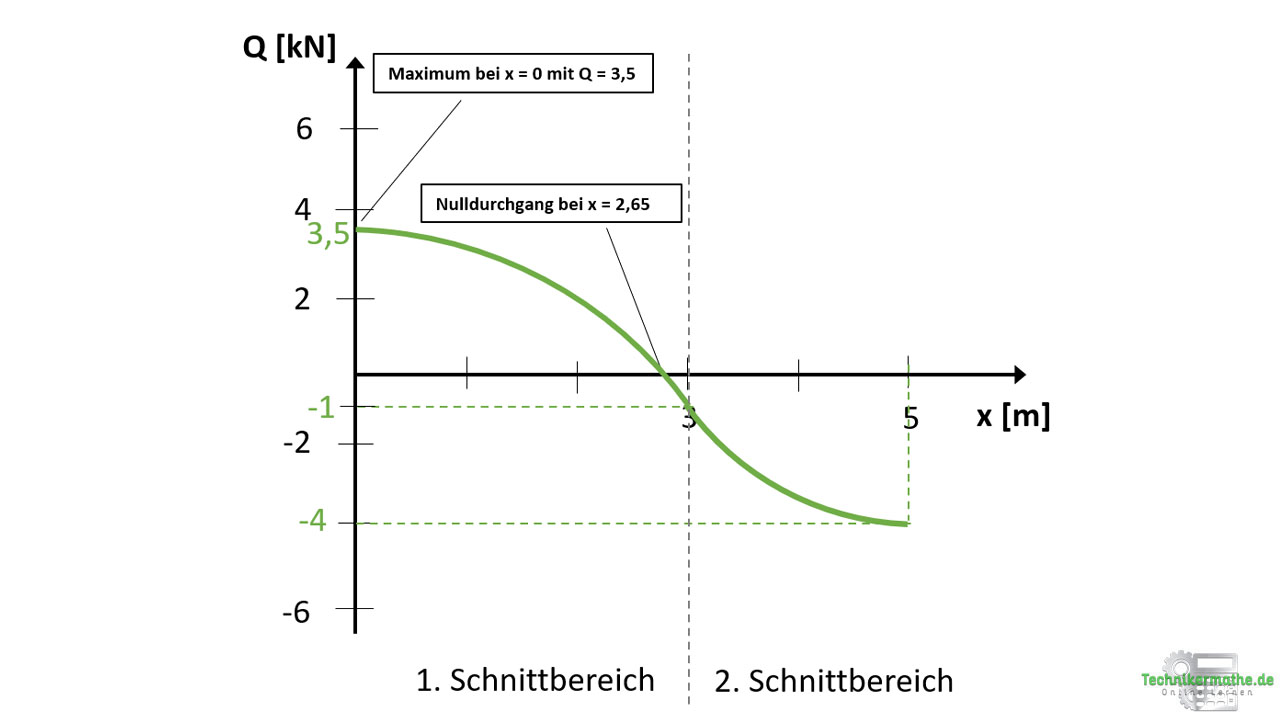
Wir können nun den Querkraftverlauf für den ersten Schnittbereich einzeichnen. Dieser beginnt bei Q = 3,5 kN, endet bei Q = -1 kN und weist einen Nulldurchgang bei x = 2,65 m auf. Außerdem ist die Parabel fallend und nach unten geöffnet:

Querkraftverlauf, Dreieckslast, Nachhilfe Statik, Schnittgrößen, Verlauf, Streckenlast, Maximum, Nulldurchgang — Querkraftverlauf: Dreieckslast im 1.Schnittbereich

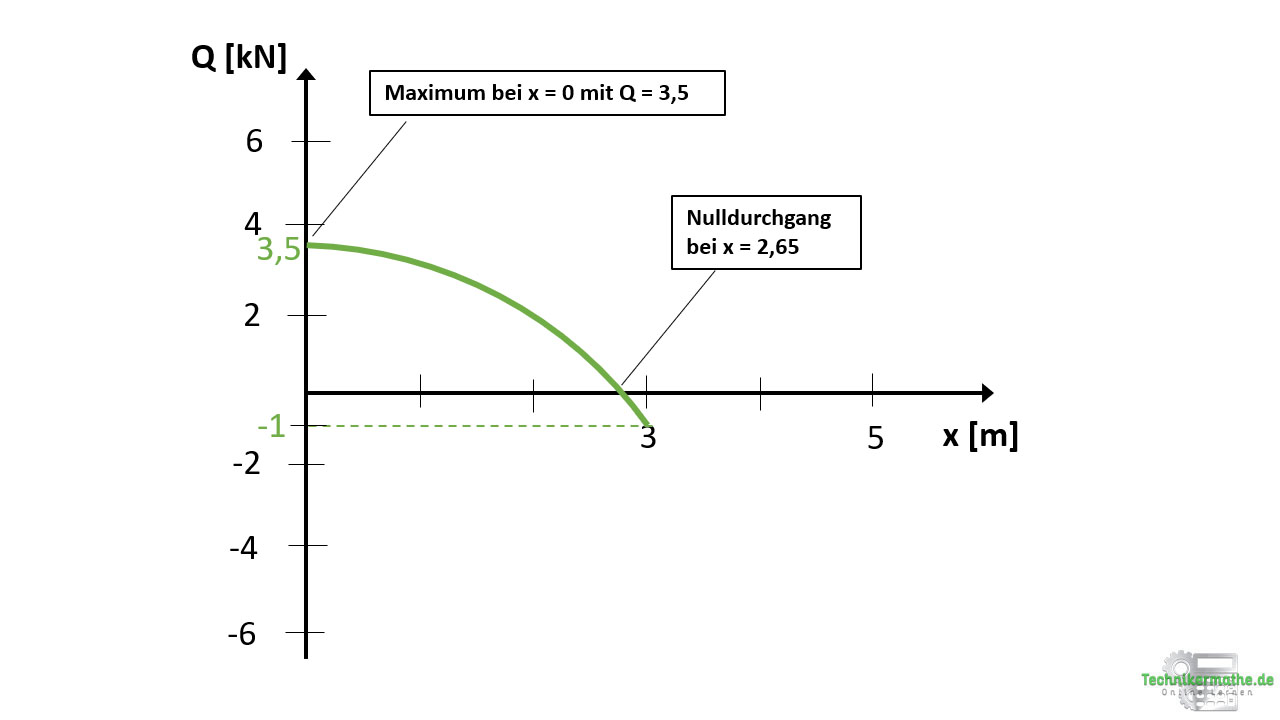
Querkraftverlauf im zweiten Schnittbereich

Im zweiten Schnittbereich ist der parabelförmige Verlauf wie folgt gegeben:

$Q_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-x)^2 - 4 kN$

Zunächst setzen wir x = 3 (Beginn der Streckenlast) und x = 5 (Ende der Streckenlast) in die Gleichung Q₂ ein, um den Beginn und das Ende des Querkraftverlaufs zu bestimmen:

$x = 3m: \; Q_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-3m)^2 - 4 kN = -1 kN$

$x = 5m: \; Q_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-5m)^2 - 4 kN = -4 kN$

Der Querkraftverlauf im zweiten Schnittbereich beginnt bei Q = -1 kN und endet bei Q = -4 kN. Dieser weist keinen Nulldurchgang auf, da der Verlauf innerhalb des negativen Bereichs verbleibt (unterhalb der x-Achse).

Minimum/Maximum bestimmen

Als nächstes wollen wir herausfinden, wo genau eine Extremstelle des Querkraftverlaufs gegeben ist. Dazu setzen wir die 1. Ableitung gleich Null und lösen nach x auf (ohne Einheiten zur besseren Übersicht):

$Q_2' = -1,5\cdot (5-x) = 0$

$-1,5\cdot (5-x) = 0$ |Klammer auflösen

$-7,5 + 1,5x = 0$ | $+7,5$

$1,5x = 7,5$ | $:1,5$

$x = 5$

Das Maximum liegt am Ende des Querkraftverlaufs Q₂ bei x = 5m. Um herauszufinden, ob es sich um eine Maximum oder Minimum handelt, betrachten wir die 2. Ableitung:

$Q_2'' = 1,5$ Minimum

Es handelt sich in diesem Fall um ein Minimum, da die zweite Ableitung größer Null ist. Die Höhe des Minimums muss mit dem Endwert des Querkraftverlaufs übereinstimmen, da beide an derselben Stelle x = 5m liegen. Um das zu überprüfen, setzen wir die Stelle des Minimums (x = 5m) in den Momentenverlauf ein:

$x = 5m: \; Q_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-5m)^2 - 4 kN = -4 kN$

Das Minimum ist bei x = 5m gegeben und ist -4 kN groß. Das Minimum zeigt uns auf, dass wir eine nach oben geöffnete Parabel für den 2. Schnittbereich gegeben haben. Da wir den Bereich vor der Minimum betrachten, handelt es sich um eine fallende nach oben geöffnete Parabel.

Für den Querkraftverlauf im 2. Schnittbereich gilt: Dieser startet bei Q = -1 kN und endet bei Q= -4 kN. Außerdem wissen wir, dass die Parabel in diesem Bereich fallend und nach oben geöffnet ist, weil das Minimum bei x = 5m gegeben ist.

Querkraftverlauf, Dreieckslast, Schnittgrößen, Nulldurchgang, Maximum — Querkraftverlauf: Dreieckslast im 2. Schnittbereich

Schnittgrößenverläufe: Momentenverlauf

Der Momentenverlauf ist in beiden Schnittbereich kubisch. Es ergibt sich also für beide Schnittbereiche eine kubische Parabel:

Momentenverlauf bei Dreieckslasten, Momentenverlauf, Schnittgrößenverläufe, Dreieckslast — Schnittgrößenverläufe: Momentenverlauf bei Dreieckslasten

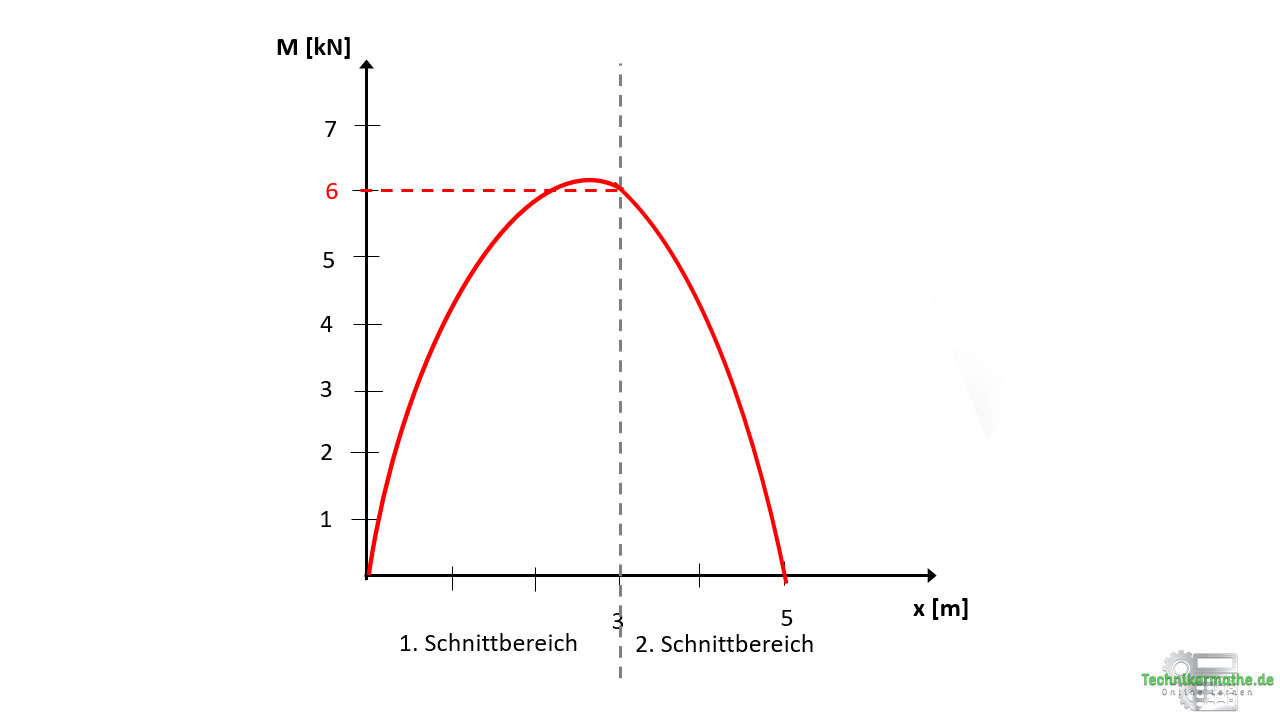
Momentenverlauf im 1. Schnittbereich

Betrachten wir zunächst einmal den kubischen Momentenverlauf im 1. Schnittbereich.

Merk’s dir!

Für den Momentenverlauf gilt allgemein:

Dort wo der Querkraftverlauf einen Nulldurchgang aufweist, liegt eine Extremstelle (Minimum oder Maximum) des Momentenverlaufs vor.

Wir wissen, dass an der Stelle x = 2,65 der Querkraftverlauf Q₁ einen Nulldurchgang aufweist. Somit ist an dieser Stelle auch ein Extremwert des Momentenverlaufs M₁ gegeben. Wir wollen nun herausfinden, ob es sich um ein Minimum oder Maximum handelt und welchen Wert der Momentenverlauf an dieser Stelle aufweist.

Maximum / Minimum bestimmen

Extremwerte werden berechnet, indem die 1. Ableitung gleich Null gesetzt wird und diese nach x aufgelöst wird. Dann haben wir die Stelle des Extremums gegeben. Dies haben wir bereits mit dem Querkraftverlauf herausgefunden (siehe oben), denn die 1. Ableitung des Momentenverlaufs ergibt den Querkraftverlauf:

$M_1' = Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2 = 0$ |nach x auflösen

Wir haben den Querkraftverlauf Q₁ bereits nach x aufgelöst und haben die folgende Stelle ermittelt:

Stelle Nulldurchgang gleich Stelle des Extremums:

x = 2,65

Um herauszufinden, ob ein Minimum oder Maximum gegeben ist, benötigen wir die 2. Ableitung:

$M_1'' = - 1 \frac{kN}{m^2}\cdot x$

Da diese noch abhängig von x ist, müssen wir hier x = 2,65m einsetzen:

$M_1'' = - 1 \frac{kN}{m^2}\cdot 2,65m = -2,65 kN/m$

Es ergibt sich ein negativer Wert. Damit liegt ein Maximum vor. Wo genau das Maximum gegeben ist, können wir aus dem Momentenverlauf M₁ durch Einsetzen von x = 2,65 m bestimmen:

$x = 2,97m: \; M_1 = 3,5 kN \cdot 2,65m- \dfrac{1}{6} \frac{kN}{m^2}\cdot (2,65m)^3 = 6,17 kNm$

An der Stelle x = 2,65m ist ein Maximum in Höhe von 6,17 kNm des Momentenverlaufs M₁ gegeben. Vor einem Maximum steigt die nach unten geöffnete Parabel, nach einem Maximum fällt diese wieder.

Wir wollen nun noch herausfinden, wo der Momentenverlauf beginnt und wo dieser endet, indem wir die Randwerte einsetzen:

$x = 0m: M_1 = 3,5 kN \cdot 0m - \dfrac{1}{6} \frac{kN}{m^2}\cdot (0m)^3 = 0 kNm$

$x = 3m: M_1 = 3,5 kN \cdot 3m - \dfrac{1}{6} \frac{kN}{m^2}\cdot (3m)^3 = 6 kNm$

Es wird deutlich, dass das Maximum nur sehr knapp über dem Endwert des Momentenverlaufs liegt. Wir haben nun alle Kenntnisse gegeben, um den Momentenverlauf für den ersten Schnittbereich einzuzeichnen. Dieser beginnt bei M = 0 kNm für x =0, steigt dann (nach unten geöffnete Parabel) bis zum Maximum von 6,17 kNm bei x = 2,65 und fällt dann auf 6 kNm bei x=3:

Momentenverlauf, Dreieckslast, Maximum, Parabel, Schnittgrößen — Momentenverlauf: Dreieckslast im 1. Schnittbereich

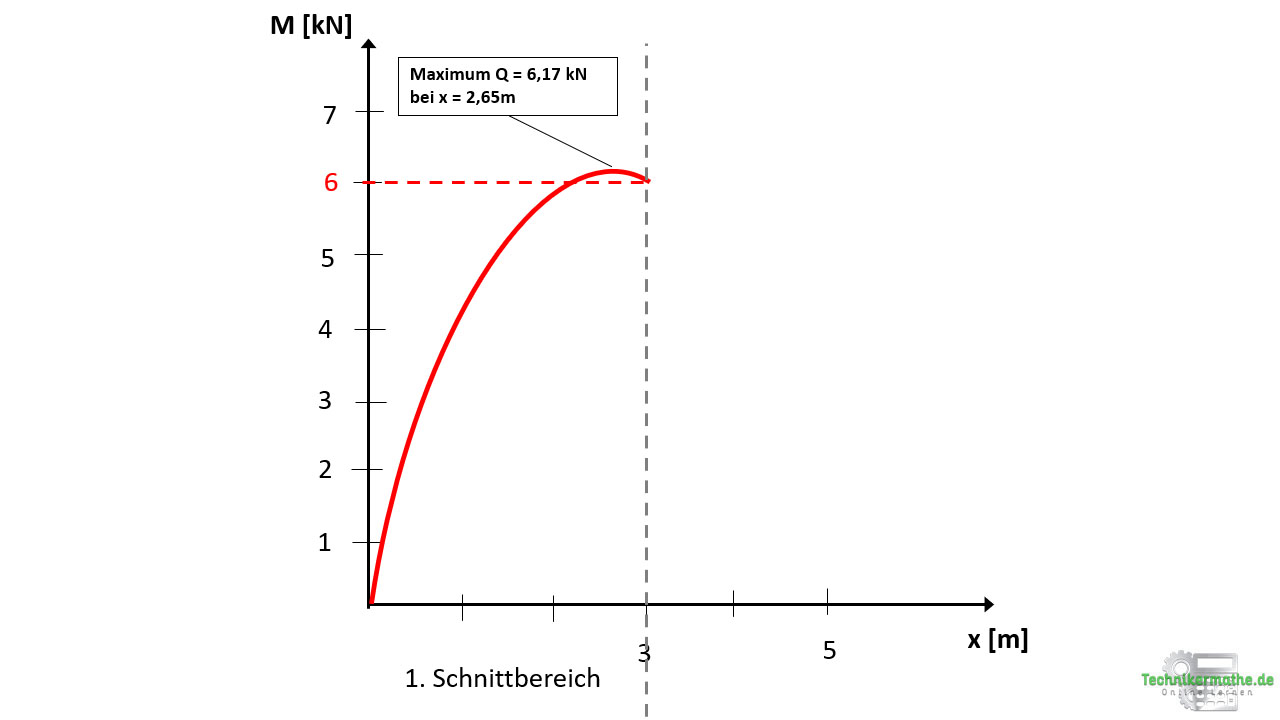
Momentenverlauf im 2.Schnittbereich

Betrachten wir zuletzt den kubischen Momentenverlauf im 2. Schnittbereich. Hier ist kein Nulldurchgang des Querkraftverlaufs Q₂ gegeben und damit besitzt der Momentenverlauf keinen Extremwert.

Die kubische Parabel ändert demnach nicht ihre Richtung. Sie setzt an den Momentenverlauf M₁ des Schnittbereichs 1 an, welcher am Ende (bei x = 3) eine nach unten geöffnete fallende Parabel darstellt. Demnach handelt es sich beim Momentenverlauf M₂ um eine nach unten geöffnete fallende Parabel.

Wir wollen nun noch herausfinden, wo der Momentenverlauf beginnt und wo dieser endet, indem wir die Randwerte einsetzen:

$x = 3m: M_2 = 4 kN \cdot (5m - 3m) - \dfrac{1}{4} \frac{kN}{m^2}\cdot (5m-3m)^3 = 6 kNm$

$x = 5m: M_2 = 4 kN \cdot (5m - 5m) - \dfrac{1}{4} \frac{kN}{m^2}\cdot (5m-5m)^3 = 0 kNm$

Der Momentenverlauf im 2. Schnittbereich beginnt bei M = 6 kNm und fällt dann (nach unten geöffnete Parabel) bis 0 kNm ab:

Momentenverlauf, Dreieckslast, kubische Parabel, Parabel, Maximum — Momentenverlauf: Dreieckslast im 2. Schnittbereich

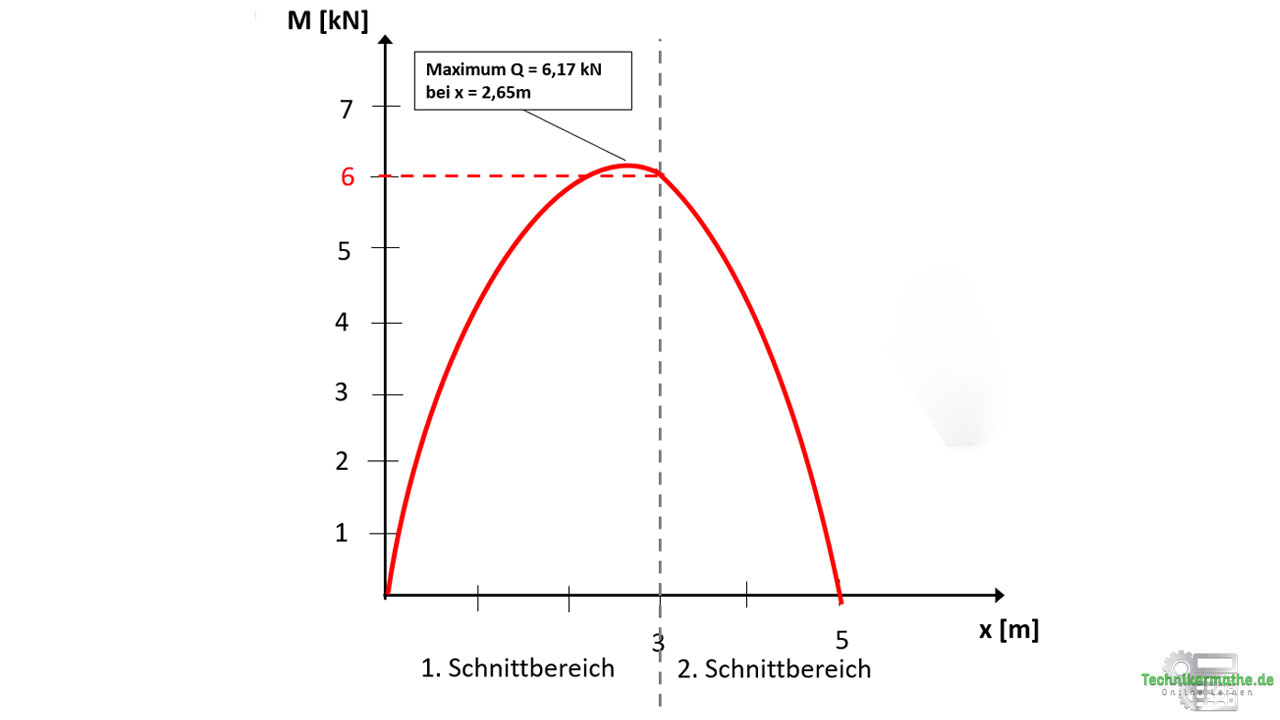
In der nächsten Lerneinheit wollen wir uns anschauen, wie die Schnittgrößen bei gegebener Streckenlast mittels Integration bestimmt werden.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++