TM1 – Schnittgrößen mit dreieckiger Streckenlast [Definition, Aufgabe, Videos, Lösung]

Bei einer Streckenlast sind Schnittgrößen die Kräfte und Momente, die an einem bestimmten Querschnitt eines Trägers oder eines Tragwerks wirken. Sie entstehen aufgrund der Belastung, die entlang der Längsachse des Trägers verteilt ist. Die wichtigsten Schnittgrößen bei Streckenlasten ist das Biegemoment (Moment, das zur Biegung führt) und die Querkraft (Kraft, die senkrecht zur Längsachse des Trägers wirkt).

In dieser Lektion erklären wir dir ausführlich und einfach das Thema Schnittgrößen bei dreieckiger Streckenlast (Dreieckslast)!

Für ein optimales Verständnis helfen dir vier ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs: TM1-Statik

Dreieckige Streckenlast – Überblick

In dieser Lerneinheit zeigen wir dir, wie du die Schnittgrößen berechnest, wenn eine dreieckige (=veränderliche) Streckenlast (auch: Dreieckslast) gegeben ist. Wir wollen dir in dieser Lerneinheit zeigen, wie du

die Resultierende der Dreieckslast aus dem Flächeninhalt bildest.
den Angriffspunkt der Resultierenden bestimmst.
die Schnittgrößen unter Anwendung des Strahlensatzes berechnest, wenn eine Dreieckslast gegeben ist.

Dreieckslast – Erklärung

Eine Dreieckslast ist dann gegeben, wenn die gegebene Streckenlast einen dreieckigen Flächeninhalt aufweist. Eine solche Streckenlast strebt an einem Ende gegen q(x) = 0 und verläuft zum anderen Ende hin mit konstanter Steigung:

Dreieckslast, Nachhilfe Techniker, dreieckige Streckenlast, Streckenlast, — Dreieckslast: Überblick

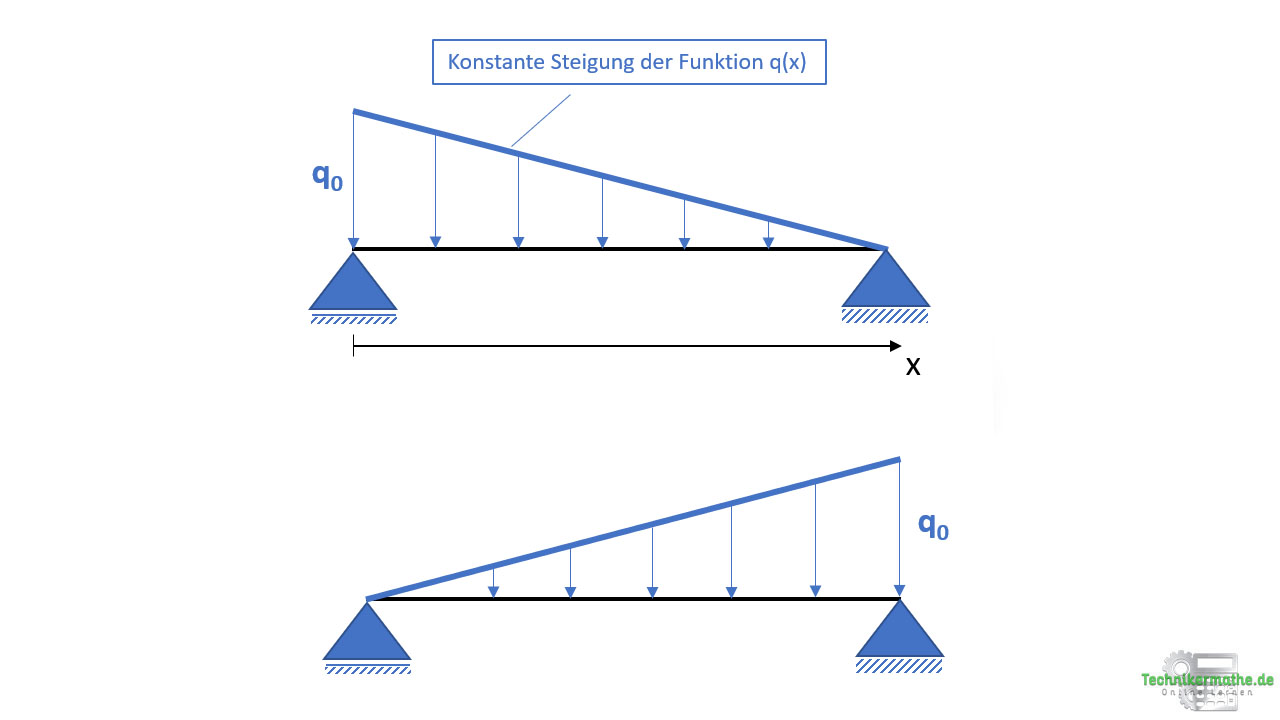
In der obigen Grafik siehst du die zwei Varianten einer Dreieckslast.

Im ersten Fall startet die Dreieckslast mit Höhe q(x) = q₀ bei x = 0 und verläuft dann mit konstanter negativer Steigung bis q(x) = 0.
Im zweiten Fall startet die Dreieckslast mit q(x) = 0 bei x = 0 und verläuft dann mit konstanter positiver Steigung bis q(x) = q₀.

Wir wollen nun zeigen, wie die Schnittgrößen berechnet werden, wenn eine Dreieckslast gegeben ist.

Videoclips: Resultierende der Dreieckslast

Bevor mit der Berechnung der Schnittgrößen begonnen werden kann, müssen zunächst die Auflagerkräfte bestimmt werden. Dazu wird die Streckenlast zu einer einzigen Kraft, der sogenannten Resultierenden zusammengefasst. Diese Resultierende ersetzt die gegebene Streckenlast und übt dieselbe Wirkung auf den Balken aus.

Wir können die Resultierende der Streckenlast über den Flächeninhalt bestimmen oder über Integration. Die erste Variante ist in jedem Fall die schnellere. Wir zeigen hier beide Varianten:

Resultierende der Dreieckslast

Willst du die Schnittgrößen in einem Balken berechnen, so musst du zunächst die Auflagerkräfte ermitteln. Um die Auflagerkräfte ermitteln zu können, musst du zunächst die Resultierende der gegebenen Streckenlast bestimmen.

Die Resultierende der Dreieckslast ist nichts anderes als der Flächeninhalt der gegebenen dreieckigen Streckenlast. Die Resultierende greift im Schwerpunkt der gegebenen dreieckigen Fläche an.

Schauen wir uns dazu mal die folgende Grafik an:

Dreieckslast, Resultierende, dreieckige Streckenlast, Resultierende der Streckenlast, Schwerpunkt — Resultierende der Dreieckslast

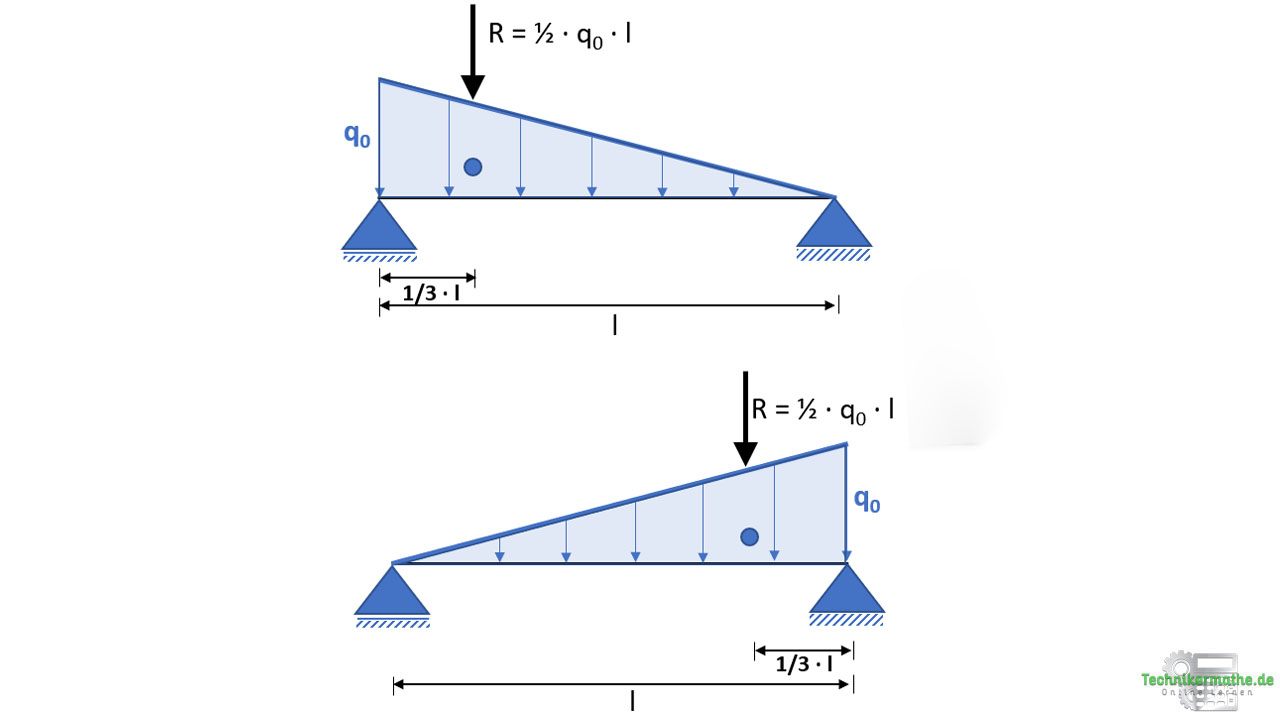
Ist eine dreieckige Streckenlast gegeben, so berechnen wir zur Bestimmung der Resultierenden den dreieckigen Flächeninhalt. Der Flächeninhalt eines Dreiecks bestimmt sich durch Höhe mal Länge durch 2. Für die dreieckige Streckenlast mit Höhe q₀ und Länge l gilt also:

Resultierende einer Dreieckslast

$R = \dfrac{1}{2} \cdot q_0 \cdot l$

mit

$q_0$ Einzellast bzw. Höhe

$l$ Länge der Dreieckslast

Wir wollen noch wissen, wo genau die Resultierende am Balken angreift. Die Resultierende einer Streckenlast greift immer im Schwerpunkt der Fläche an. Wir haben hier eine dreieckige Fläche gegeben. Bei einem Dreieck liegt die Schwerpunkt bei 1/3 der Länge, ausgehend vom rechten Winkel. Da uns nur der horizontale Abstand interessiert, greift die Resultierende also bei einem Drittel der Länge der Streckenlast an:

Angriffspunkt bei 1/3 l ausgehend vom rechten Winkel (Dreieckslast)

Merk’s dir!

Die Resultierende der Streckenlast ersetzt die Streckenlast. Du musst nun nicht extra eine neue Skizze anfertigen und den Balken ohne Streckenlast skizzieren. Du kannst statt dessen auch einfach die Resultierende oberhalb der Streckenlast einzeichnen, so wie in der obigen Grafik gezeigt.

Videoclip – Lagerkräfte bei Dreieckslast

Im folgenden Video zeigen wir dir ausführlich, wie du die Auflagerkräfte bei einer gegebenen Dreieckslast bestimmst.

Videoclips – Schnittgrößen bei Dreieckslast

In der folgenden Videoreihe behandeln wir einen Kragarm, auf welchen eine Dreieckslast wirkt. Wir zeigen dir, wie du die Auflagerkräfte und Schnittgrößen berechnest.

Wir wollen uns das Vorgehen aber auch nochmal an einem weiteren Beispiel anschauen.

Beispiel: Schnittgrößen bei Dreieckslast

Beispiel: Schnittgrößen bei Dreieckslast

Dreieckslast: Beispiel, dreieckige Streckenlast, Dreieckslast, Beispiel, Berechnung — Beispiel: Schnittgrößen bei Dreieckslast

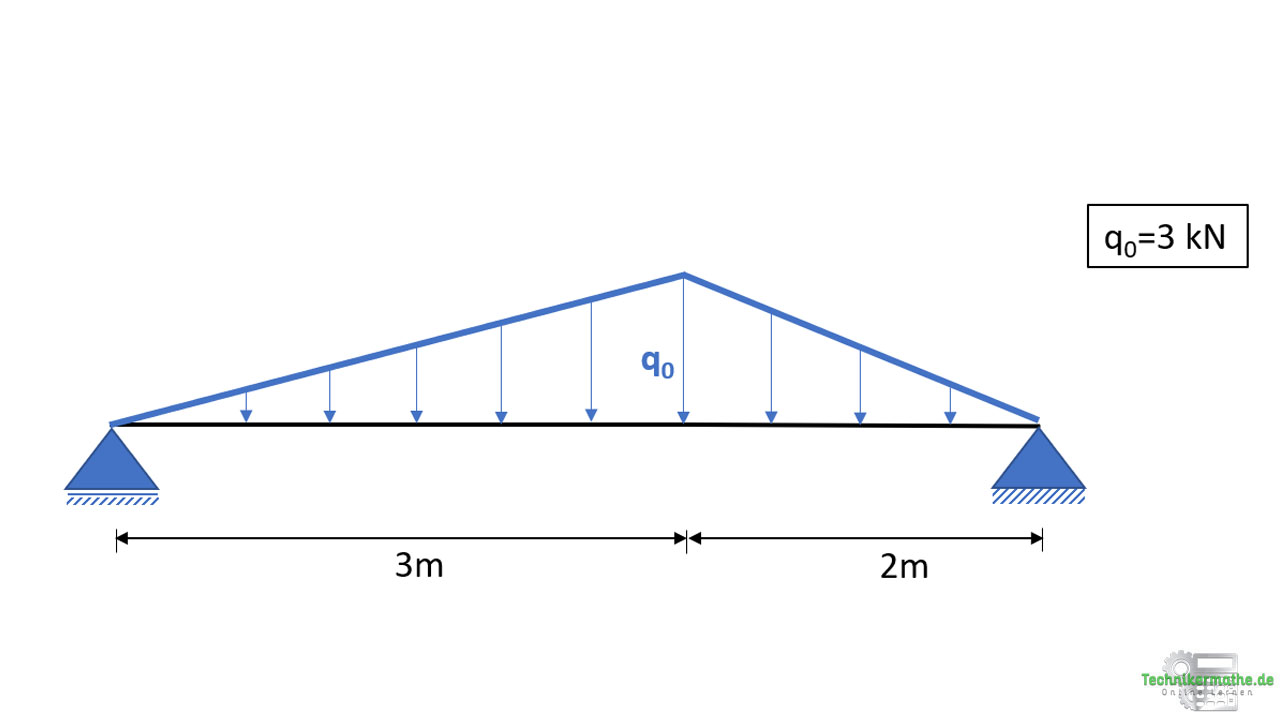
Gegeben sei der obige Balken, an welchen eine Streckenlast mit q₀ = 3 kN/m angreift.

Wir wollen für den gesamten Balken die Schnittgrößen bestimmen und die Schnittgrößenverläufe angeben.

Wir können die obige Streckenlast in zwei Dreiecklasten aufteilen.

Freischnitt und Resultierende der Dreieckslasten

Zunächst schneiden wir den Balken von seinen Auflagern frei und bestimmen die beiden Resultierenden der Dreieckslasten:

Freischnitt, Resultierende, Auflagerkräfte, Streckenlast, Dreieckslast, Schwerpunkt — Freischnitt und Resultierende

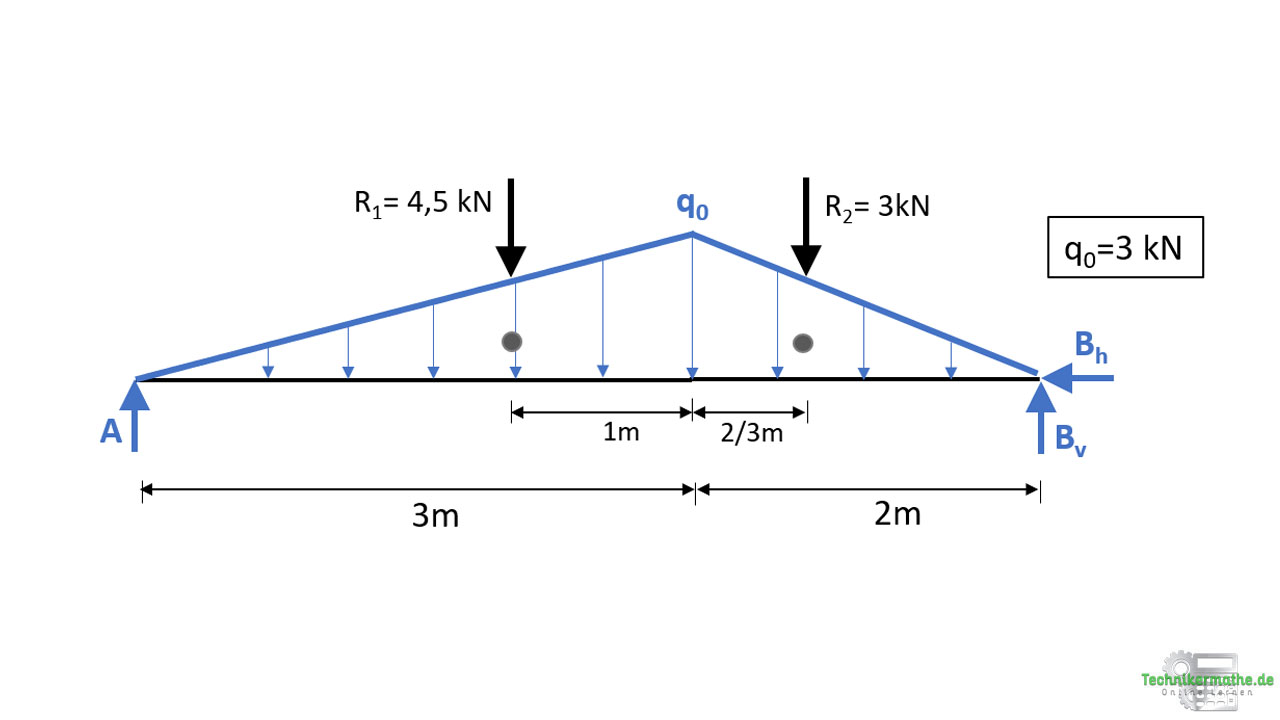
Die Resultierenden der Dreieckslasten entsprechen dem Flächeninhalt der dreieckigen Flächen. Es wird der Flächeninhalt eines Dreiecks herangezogen:

$A_D = \frac{1}{2} \cdot h \cdot l$

Hierbei ist h die Höhe (hier: q0) und l die Länge (hier: 3m und 2m). Es ergibt sich somit für die beiden Dreieckslasten:

$R_1 = \dfrac{1}{2} \cdot q_0 \cdot l = \dfrac{1}{2} \cdot 3 \frac{kN}{m} \cdot 3m = 4,5 kN$

$R_2 = \dfrac{1}{2} \cdot q_0 \cdot l = \dfrac{1}{2} \cdot 3 \frac{kN}{m} \cdot 2m = 3 kN$

Nachdem wir die Resultierenden der beiden Streckenlasten berechnet haben, benötigen wir als nächstes die Angriffspunkte dieser.

Merk’s dir!

Es gilt grundsätzlich: Der Angriffspunkt der Resultierenden einer Streckenlast liegt im Schwerpunkt der Fläche der Streckenlast.

Der Schwerpunkt eines Dreiecks liegt bei einem Drittel der Länge, ausgehend vom rechten Winkel. In der obigen Grafik siehst du also, wo genau die Resultierenden angreifen müssen.

Bestimmung der Auflagerkräfte

Freischnitt, dreieckige Streckenlast, Auflagerkräfte, Beispiel, Schnittgrößen — Auflagerkräfte bestimmen

Im nächsten Schritt müssen wir die Auflagerkräfte berechnen. Dazu wenden wir die drei Gleichgewichtsbedingungen in der Ebene an.

Gleichgewichtsbedingung in x-Richtung

Die Summe aller Kräfte in x-Richtung muss null ergeben:

$\sum F_{ix} = 0$

Wir wählen die Vorzeichenkonvention, dass alle nach rechts wirkenden Kräfte positiv und alle nach links wirkenden Kräfte negativ berücksichtigt werden.

$-B_h = 0$

Die Auflagerkraft B_h wird zu Null, da keine horizontalen Kräfte an den Balken angreifen.

Gleichgewichtsbedingung in y-Richtung

Die Summe aller Kräfte in y-Richtung muss null ergeben:

$\sum F_{iy} = 0$

Wir wählen die Vorzeichenkonvention, dass alle nach oben wirkenden Kräfte positiv und alle nach unten wirkenden Kräfte negativ berücksichtigt werden.

$A - R_1 - R_2 + B_v = 0$

Aus der Gleichgewichtsbedingung in y-Richtung können wir noch keine unbekannte Auflagerkraft ermitteln, da hier A und B_v unbekannt sind. Demnach wenden wir zunächst die Momentengleichgewichtsbedingung an.

Momentengleichgewichtsbedingung um A

Die Summe aller Momente auf einen gewählten Bezugspunkt X muss null ergeben:

$\sum M^X = 0$

Wir wählen die Vorzeichenkonvention, dass alle linksdrehenden Momente positiv und alle rechtsdrehenden Momente negativ berücksichtigt werden.

$\sum M^X = 0$

$-R_1 \cdot 2m - R_2 \cdot (3m + 2/3m) + B_v \cdot 5m = 0$

$B_v \cdot 5m = R_1 \cdot 2m + R_2 \cdot (3m + 2/3m)$

$B_v = \dfrac{R_1 \cdot 2m + R_2 \cdot (11/3 m)}{5m}$

$B_v = \dfrac{4,5 kN \cdot 2m + 3 kN \cdot (11/3 m)}{5m}$

$B_v = 4 kN$

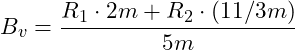
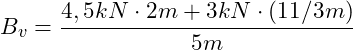
Aus der Gleichgewichtsbedingung in y-Richtung können wir nun die unbekannte Auflagerkraft A berechnen:

$A - R_1 - R_2 + B_v = 0$

$A = R_1 + R_2 - B_v$

$A = 4,5 kN + 3 kN - 4 kN$

$A = 3,5 kN$

Bestimmung der Schnittgrößenverläufe

Wir müssen nun als nächstes gedankliche Schnitte durch den Balken durchführen und die Schnittgrößen am linken/rechten Schnittufer abtragen. Geschnitten wird immer:

zwischen Einzellasten (äußere Lasten, Auflagerkräfte)
durch Streckenlasten.

Da wir keine Einzellasten gegeben haben und zwischen den Streckenlasten kein Lücke gegeben ist, schneiden wir wie folgt:

Schnittgrößen, Dreieckslast, Schnittufer, Normalkraft, Querkraft, Moment — Schnittgrößen bei Dreieckslast

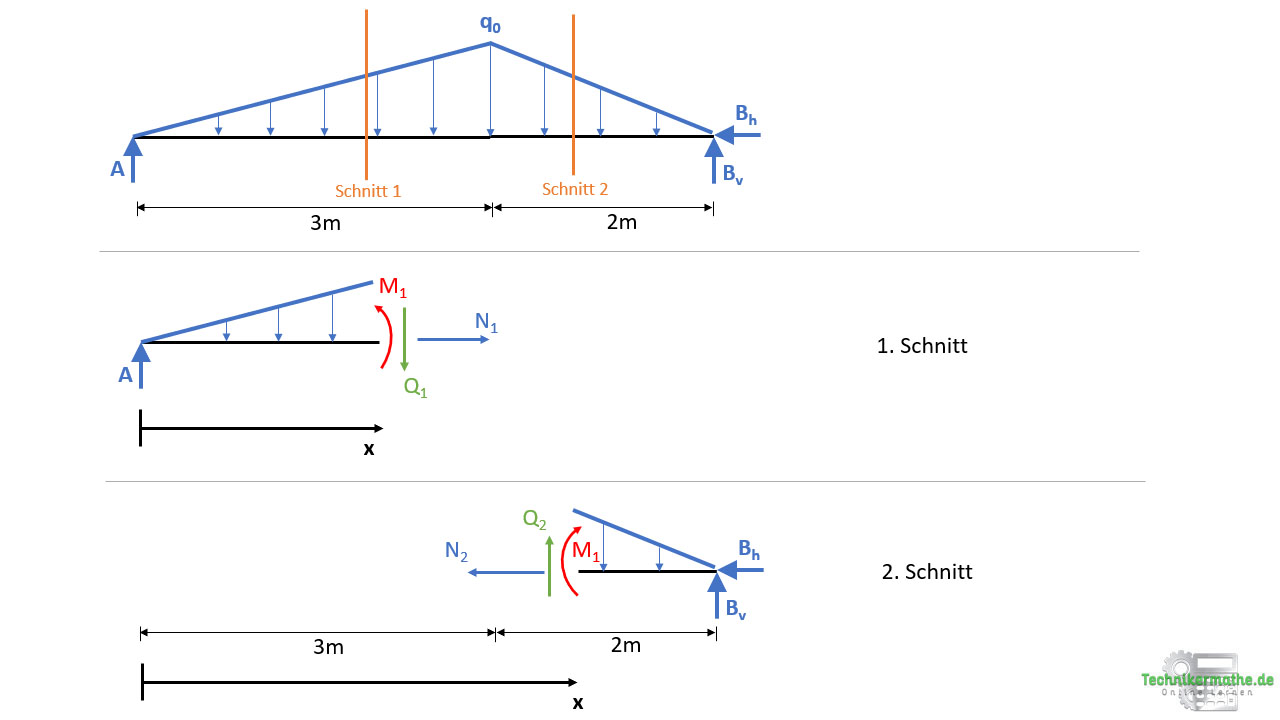
In der obigen Grafik führen wir die Schnitte durch die beiden Dreieckslasten durch. Es ergeben sich demnach zwei Schnitte. Da wir für die Berechnung der Schnittgrößen mittels Strahlensatz immer die dreieckige Teilstreckenlast benötigen, wenden wir für den 1. Schnitt das linke Schnittufer und für den 2. Schnitt das rechte Schnittufer an.

Der 1. Schnitt wird zwischen 0 ≤ x ≤ 3m durchgeführt, der 2. Schnitt zwischen 3m ≤ x ≤ 5m.

Schnitt 1: 0 ≤ x ≤ 3m

Wir starten mit dem 1. Schnitt. Dort haben wir eine dreieckige Teilstreckenlast gegeben. Diese weist nun aber nicht mehr die Höhe q₀ auf, sondern eine Höhe q₁(x), die abhängig davon ist, wo wir den Schnitt genau durchführen (also von x).

Diese Höhe müssen wir zunächst berechnen. Hier können wir den 2.Strahlensatz anwenden:

2. Strahlensatz!

Strahlensätze können nur angewandt werden, wenn zwei (oder mehrere) Strahlen einen gemeinsamen Schnittpunkt besitzen. Zusätzlich müssen diese Strahlen von zwei parallelen Geraden gekreuzt werden.

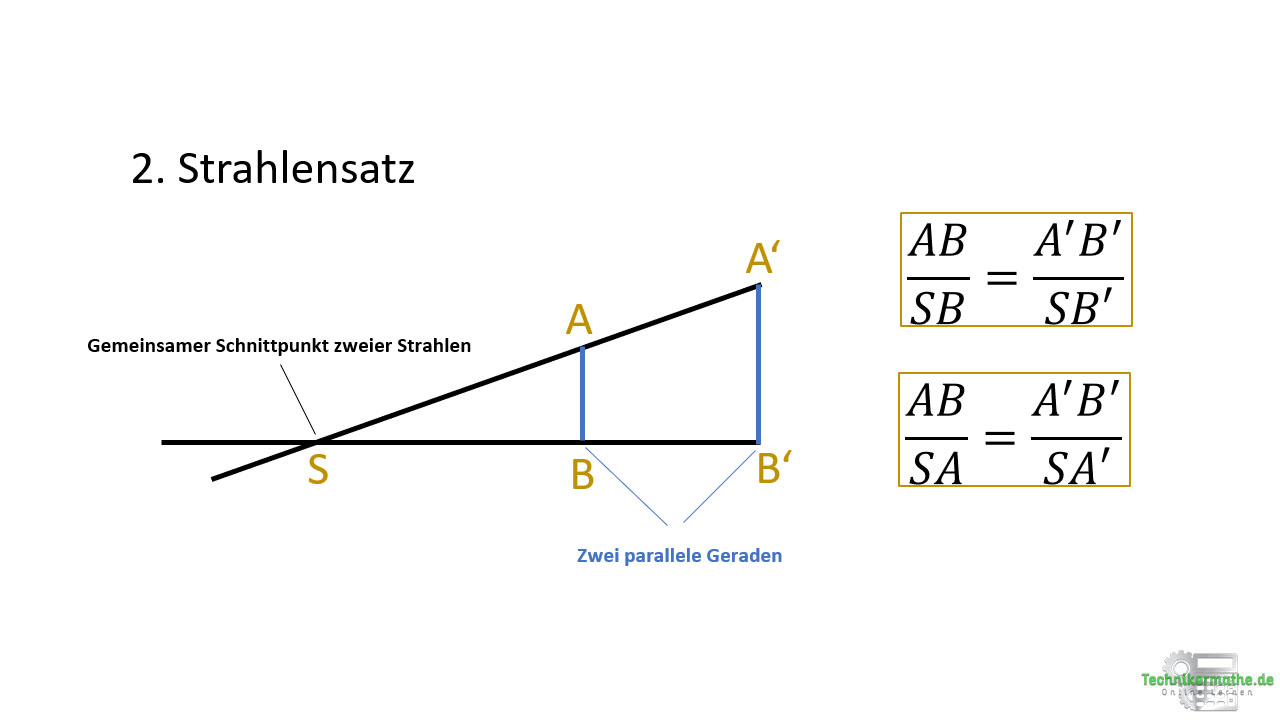
Aus der ersten Gleichung lesen wir: Das Verhältnis der Strecke AB und SB ist gleich dem Verhältnis der Strecke A’B’ und SB’.

Aus der zweiten Gleichung lesen wir: Das Verhältnis der Strecke AB und SA ist gleich dem Verhältnis der Strecke A’B’ und SA’.

Auf unser Beispiel können wir den 2. Strahlensatz dann wie folgt anwenden:

Strahlensatz, Schnittgrößen, Streckenlast, Berechnung, Beispiel, Teilstreckenlast — Anwendung des zweiten Strahlensatzes zur Berechnung der Teilstreckenlast

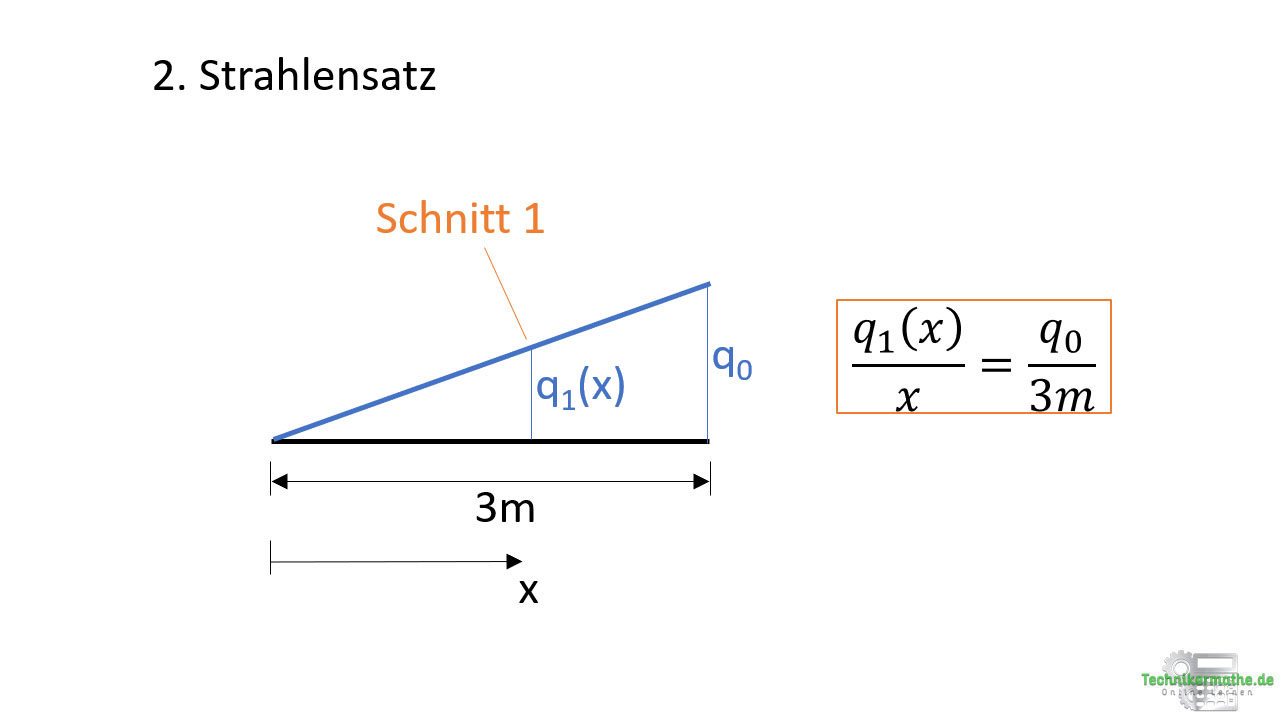
Wir betrachten die gesamte Dreieckslast mit Länge 3m und Höhe q₀ und zeichnen außerdem die Höhe q1(x) ein, die beim Schnitt 1 gegeben ist. Die Länge dieser dreieckigen Teilstreckenlast ist dabei durch die x-Achse gegeben.

Das Verhältnis aus der Teilhöhe q₁(x) und der Teilstrecke x ist genau so groß, wie das Verhältnis aus der Gesamthöhe q₀ und der Gesamtlänge 3m:

$\dfrac{q_1(x)}{x} = \dfrac{q_0}{3m}$

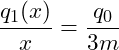
Wir können nun nach der gesuchten Höhe q₁(x) auflösen:

$q_1(x) = \dfrac{q_0}{3m} \cdot x$

Einsetzen von q₀ = 3 kN/m:

$q_1(x) = 1 kN/m^2 \cdot x$

Wir kennen nun also die Höhe der Teilstreckenlast und können als nächstes die Resultierende dieser Teilstreckenlast und den Angriffspunkt der Resultierenden berechnen:

Schnittgrößen, Resultierende, Schnittufer, Streckenlast — Schnitt 1: Resultierende der Teilstreckenlast

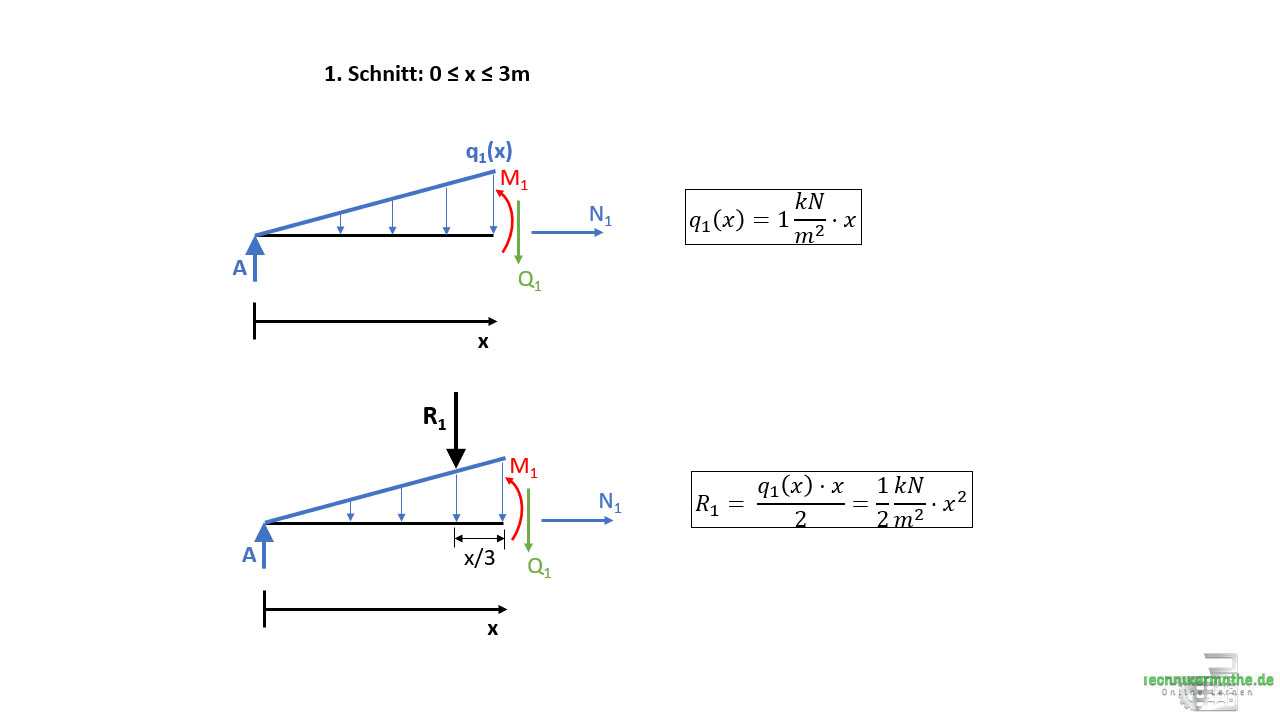
Wir haben in der obigen Grafik den ersten Schnitt gegeben, mit der Teilstreckenlast mit Höhe q₁(x) sowie der Länge x. Wir bilden dann die Resultierende dieser Teilstreckenlast, indem wir den Flächeninhalt berechnen. Der Flächeninhalt eines Dreiecks ist gegeben zu:

Flächeninhalt eines Dreiecks

$A_D = \dfrac{h \cdot l}{2}$

mit

h = Höhe

l = Länge

Für unseren Fall gilt also:

Berechnung der Resultierenden einer Dreieckslast

$R_1 = \dfrac{q_1(x) \cdot x}{2}$

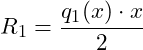
mit

q₁(x) = Höhe

x = Länge

Danach setzen wir q₁(x) ein und erhalten:

$R_1 = \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2$

Der Angriffspunkt der Resultierenden liegt im Schwerpunkt der Fläche. Bei einer dreieckigen Fläche also vom rechten Winkel ausgehend bei einem Drittel der Länge:

$\dfrac{x}{3}$ Angriffspunkt vom rechten Winkel ausgehend

Im nächsten Schritt können wir nun die Schnittgrößen aus den Gleichgewichtsbedingungen bestimmen.

Horizontale Gleichgewichtsbedingung:

$N_1 = 0$

Vertikale Gleichgewichtsbedingung:

$A - R_1 - Q_1 = 0$

$Q_1 = A - R_1$

$Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2$

Momentengleichgewichtsbedingung:

$-A \cdot x + R_1 \cdot \dfrac{x}{3} + M_1 = 0$

$M_1 = A \cdot x - R_1 \cdot \dfrac{x}{3}$

Einsetzen von R₁ und A:

$M_1 = 3,5 kN \cdot x - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2 \cdot \dfrac{x}{3}$

$M_1 = 3,5 kN \cdot x - \dfrac{1}{6} \frac{kN}{m^2}\cdot x^3$

Ist eine dreieckige Streckenlast gegeben, so liegt ein quadratischer Querkraftverlauf und ein kubischer Momentenverlauf vor.

Schnitt 2: 3m ≤ x ≤ 5m

Zunächst wollen wir wieder die Teilhöhe q₂(x) der dreieckigen Teilstreckenlast bestimmen. Dazu wenden wir den 2. Strahlensatz an. Weil die x-Achse am Balkenanfang beginnt und wir das rechte Schnittufer betrachten, müssen wir hier die gesamten Abmessungen des Balkens (5m) berücksichtigen, um die Länge der Teilstreckenlast (x – 5m ) zu bestimmen.

Strahlensatz, Resultierende, dreieckige Streckenlast, Streckenlast, Schnittgrößen — Strahlensatz: Schnitt 2

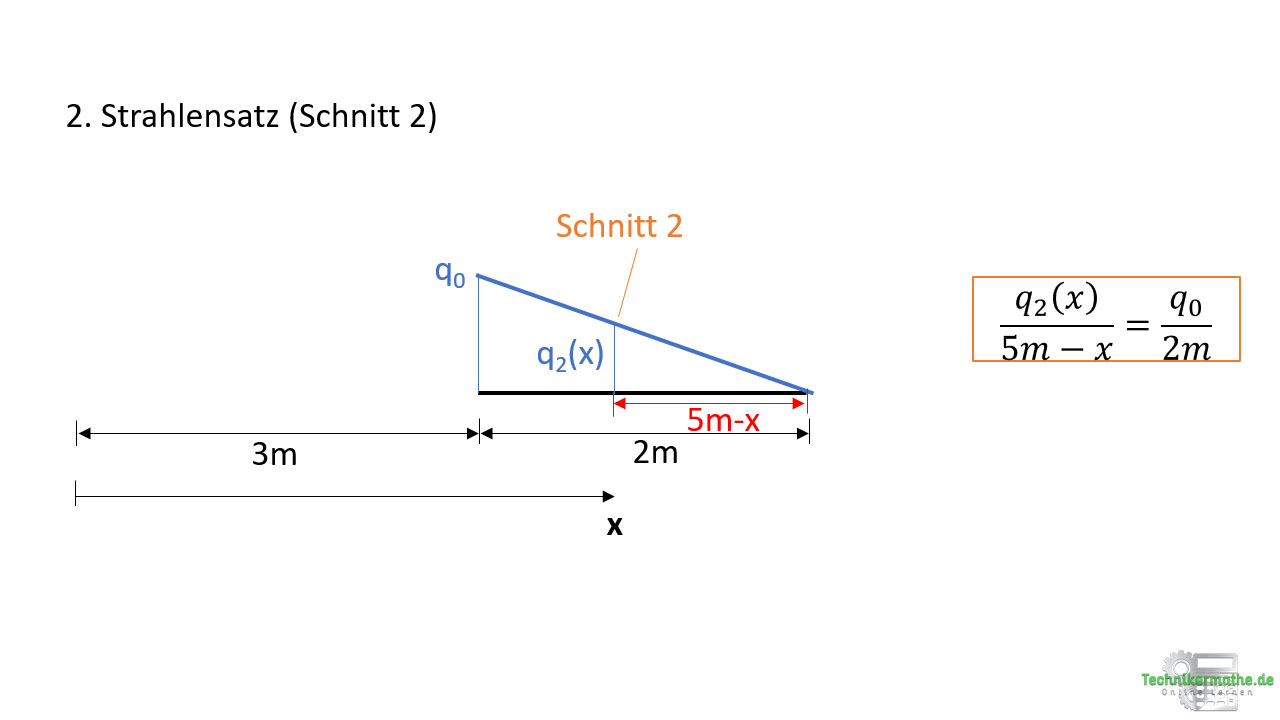
Wir betrachten die gesamte Dreieckslast mit Länge 2m und Höhe q₀ und zeichnen außerdem die Höhe q₂(x) ein, die beim Schnitt 2 gegeben ist. Die Länge dieser dreieckigen Teilstreckenlast ist dabei durch die x-Achse sowie die Gesamtabmessung gegeben.

Das Verhältnis aus der Teilhöhe q₂(x) und der Teilstrecke (5m-x) ist genau so groß, wie das Verhältnis aus der Gesamthöhe q₀ und der Gesamtlänge 2m:

$\dfrac{q_2(x)}{5m-x} = \dfrac{q_0}{2m}$

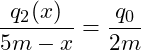
Wir können nun nach der gesuchten Höhe q₂(x) auflösen:

$q_2(x) = \dfrac{q_0}{2m} \cdot (5m-x)$

Einsetzen von q₀ = 3 kN/m:

$q_2(x) = \dfrac{3}{2} \dfrac{kN}{m^2} \cdot (5m-x)$

Wir kennen nun also die Höhe der Teilstreckenlast und können als nächstes die Resultierende dieser Teilstreckenlast und den Angriffspunkt der Resulierenden berechnen:

Schnittgrößen, Schnittufer, Resultierende der Streckenlast, Resultierende — Schnitt 2: Resultierende der dreieckigen Streckenlast

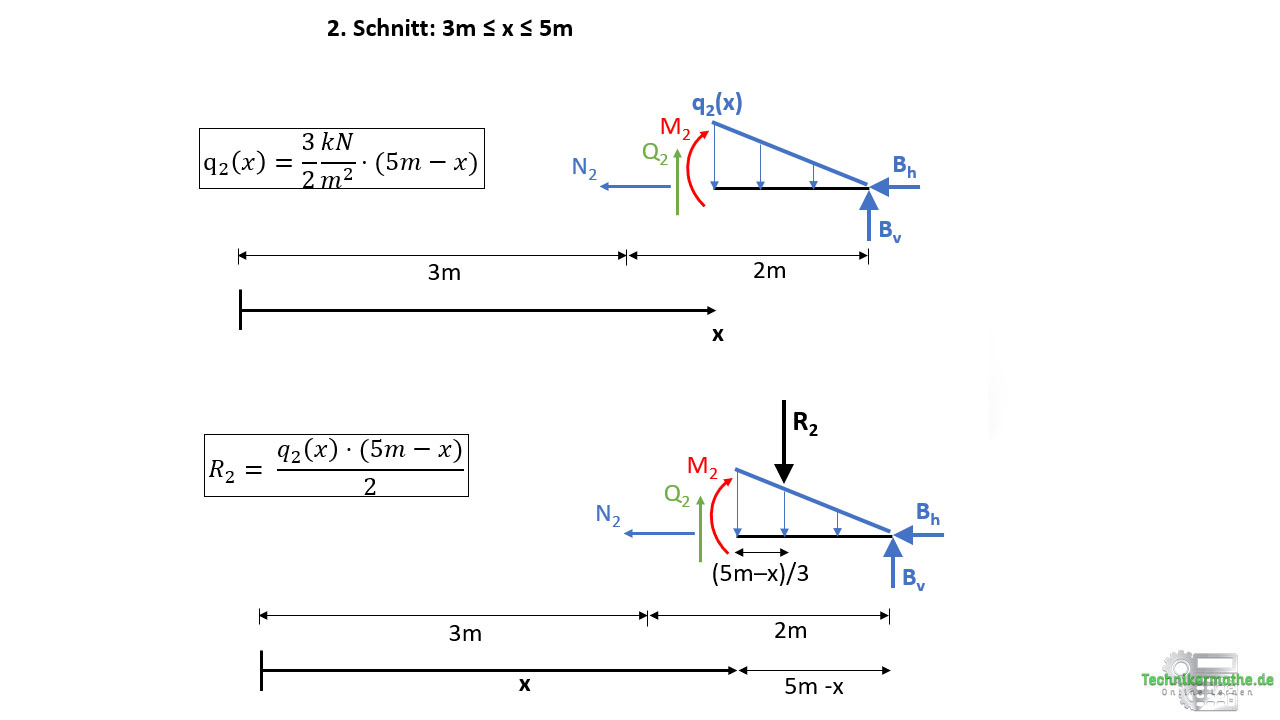
Wir haben in der obigen Grafik den ersten Schnitt gegeben, mit der Teilstreckenlast mit Höhe q₂(x) sowie der Länge (5m-x). Wir bilden dann die Resultierende dieser Teilstreckenlast, indem wir den Flächeninhalt berechnen:

$R_2 = \dfrac{q_2(x) \cdot (5m-x)}{2}$

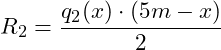
mit

q₂(x) = Höhe

(5m-x) = Länge

Danach setzen wir q₂(x) ein und erhalten:

$R_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-x) \cdot (5m-x)$

$R_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-x)^2$ Resultierende der Teilstreckenlast

Der Angriffspunkt der Resultierenden liegt im Schwerpunkt der Fläche. Bei einer dreieckigen Fläche also vom rechten Winkel ausgehend bei einem Drittel der Länge:

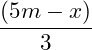$\dfrac{(5m-x)}{3}$ Angriffspunkt vom rechten Winkel ausgehend

Im nächsten Schritt können wir nun die Schnittgrößen aus den Gleichgewichtsbedingungen bestimmen.

Horizontale Gleichgewichtsbedingung:

$-N_2 -B_h = 0$

$N_2 = - B_h = 0$

Vertikale Gleichgewichtsbedingung:

$B_v - R_2 + Q_2 = 0$

$Q_2 = R_2 - B_v$

$Q_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-x)^2 - 4 kN$

Momentengleichgewichtsbedingung:

$B_v \cdot (5m - x) - R_2 \cdot \dfrac{5m - x}{3} - M_2 = 0$

$M_2 = B_v \cdot (5m - x) - R_2 \cdot \dfrac{5m - x}{3}$

Einsetzen von R₂ und B_v:

$M_2 = 4 kN \cdot (5m - x) - \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-x)^2 \cdot \dfrac{5m - x}{3}$

$M_2 = 4 kN \cdot (5m - x) - \dfrac{1}{4} \frac{kN}{m^2}\cdot (5m-x)^3$

Ist eine dreieckige Streckenlast gegeben, so liegt ein quadratischer Querkraftverlauf und ein kubischer Momentenverlauf vor.

Damit sind alle Schnittgrößen für die beiden Schnittgrößenbereiche bestimmt.

	Schnitt 1	Schnitt 2
Normalkraftverlauf	$N_1 = 0$	$N_2 = 0$
Querkraftverlauf	$Q_1 = 3,5 kN - \dfrac{1}{2} \frac{kN}{m^2}\cdot x^2$	$Q_2 = \dfrac{3}{4} \frac{kN}{m^2}\cdot (5m-x)^2 - 4 kN$
Momentenverlauf	$M_1 = 3,5 kN \cdot x - \dfrac{1}{6} \frac{kN}{m^2}\cdot x^3$	$M_2 = 4 kN \cdot (5m - x) - \dfrac{1}{4} \frac{kN}{m^2}\cdot (5m-x)^3$

Was kommt als Nächstes?

In der nächsten Lerneinheit wollen wir uns anschauen, wie die Schnittgrößenverläufe grafisch eingezeichnet werden unter Berücksichtigung der Extremwerte der Verläufe sowie des Nulldurchgangs des Querkraftverlaufes.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++