TM1 | Schnittufer, Schnittgrößen & Schnittgrößenverläufe [Grundlagen, Aufgaben, Lernclips, Tipps]

Schnittgrößen sind Kräfte die im Inneren eines Bauteils entstehen, wenn äußere Kräfte auf das Bauteil wirken. Normalkraft, Querkraft und Biegemoment sind die drei auftretenden Schnittgrößen und können aus den Gleichgewichtsbedingungen berechnet werden.

In dieser Lerneinheit führen wir die drei Schnittgrößen ein und zeigen, wie diese an den Schnittufern abgetragen werden. Außerdem folgt ein Berechnungsbeispiel inklusive Berechnung sowie Einzeichnung der Schnittgrößenverläufe bei einer gegebenen Einzelkraft.

Für ein optimales Verständnis helfen dir ein Videoclip und eine anschauliche und ausführlich gelöste Klausuraufgabe zu dem Thema.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.

Auch Interessant! Werkstofftechnik findest du im Kurs: WT3-Werkstoffprüfung

++ Lernclip | Linkes und rechtes Schnittufer ++

Im folgenden Video schauen wir uns das rechte und linke Schnittufer an.

Schnittgrößen – Grundlagen

Was sind Schnittgrößen?

Schnittgrößen sind interne Kräfte und Momente, die in einem tragenden Bauteil wirken, wenn es durch äußere Lasten beansprucht wird. Sie sind entscheidend für die Statik und Festigkeitslehre und umfassen Normalkraft, Querkraft und Biegemoment.

Schnittgrößen berechnen | linkes Schnittufer, rechtes Schnittufer

Wirken äußeren Kräfte auf einen Balken, so entstehen auch im Inneren des Balkens Kräfte. Diese inneren Kräfte werden als Schnittgrößen bezeichnet und beschreiben die Wirkung von äußeren Kräften und Momenten im Inneren des Balkens.

Um diese inneren Kräfte berechnen zu können, wird ein gedanklicher Schnitt durch den Balken durchgeführt. Durch diesen gedanklichen Schnitt werden die Schnittgrößen am linken und rechten Teilbalken freigelegt.

Schnittgrößen und Schnittufer | Erklärung

Es treten insgesamt drei Schnittgrößen auf:

Normalkraft N,
Querkraft Q und
Biegemoment M.

Betrachten wir einen Balken und führen einen gedanklichen Schnitt durch den Balken durch, so ergibt sich ein linkes Schnittufer und ein rechtes Schnittufer:

Schnittufer, rechtes Schnittufer, linkes Schnittufer, Schnittgrößen

Am linken Schnittufer zeigt die Querkraft Q nach unten, die Normalkraft N nach rechts und das Moment M ist ein linksdrehendes. Am rechten Schnittufer werden die Schnittgrößen genau entgegengesetzt abgetragen.

Merk’s dir!

Infolge des Wechselwirkungsprinzips (3. Newtonsches Gesetz) müssen an beiden Schnittufern die Schnittgrößen betragsmäßig übereinstimmen, wirken aber genau entgegengesetzt zueinander.

Statt Schnittfläche wird in den meisten Fällen von Schnittufer gesprochen.

Die Trennung des Balkens erfolgt natürlich gedanklich, um die Schnittgrößen berechnen zu können.

Damit sich der Balken weder verformt noch knickt müssen die inneren Kräfte (Schnittgrößen) den äußeren Kräften standhalten. Damit herrscht ein Gleichgewicht zwischen den inneren und äußeren Kräften und wir können zur Berechnung der Schnittgrößen die Gleichgewichtsbedingungen anwenden.

Schauen wir uns zum Verständnis mal ein einfaches Beispiel an.

Aufgabe | Schnittgrößen berechnen

Aufgabenstellung

Schnittgrößen Beispiel, Nachhilfe Techniker, Statik, Schnittgrößen, schräge Kraft, Balken, Einführung — Aufgabe: Schnittgrößen berechnen

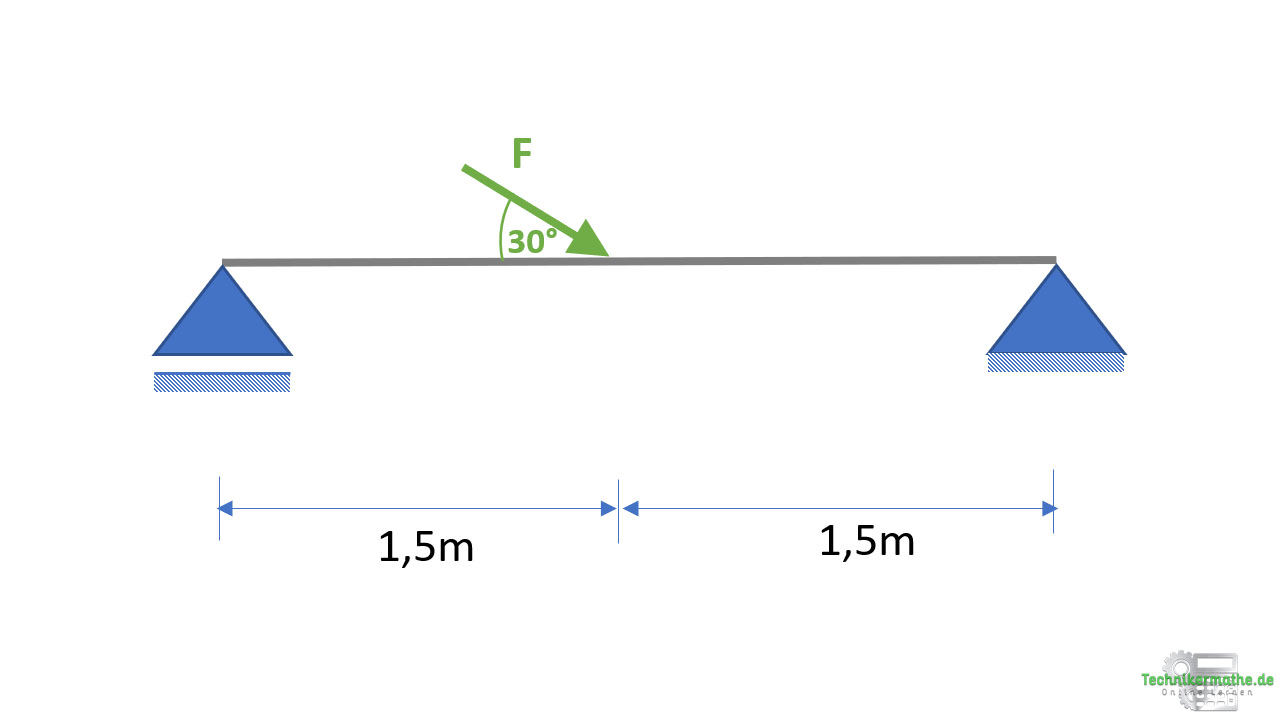
Gegeben sei der obige Balken, auf welche eine äußere Kraft F = 3 kN mittig mit einem Winkel von 30° zur Horizontalen angreift.

Bestimme die Schnittgrößen im gesamten Balken!

Lösung

Kräftezerlegung durchführen

Schnittgrößen, Kräftezerlegung, Einführung Schnittgrößen — Kräftezerlegung

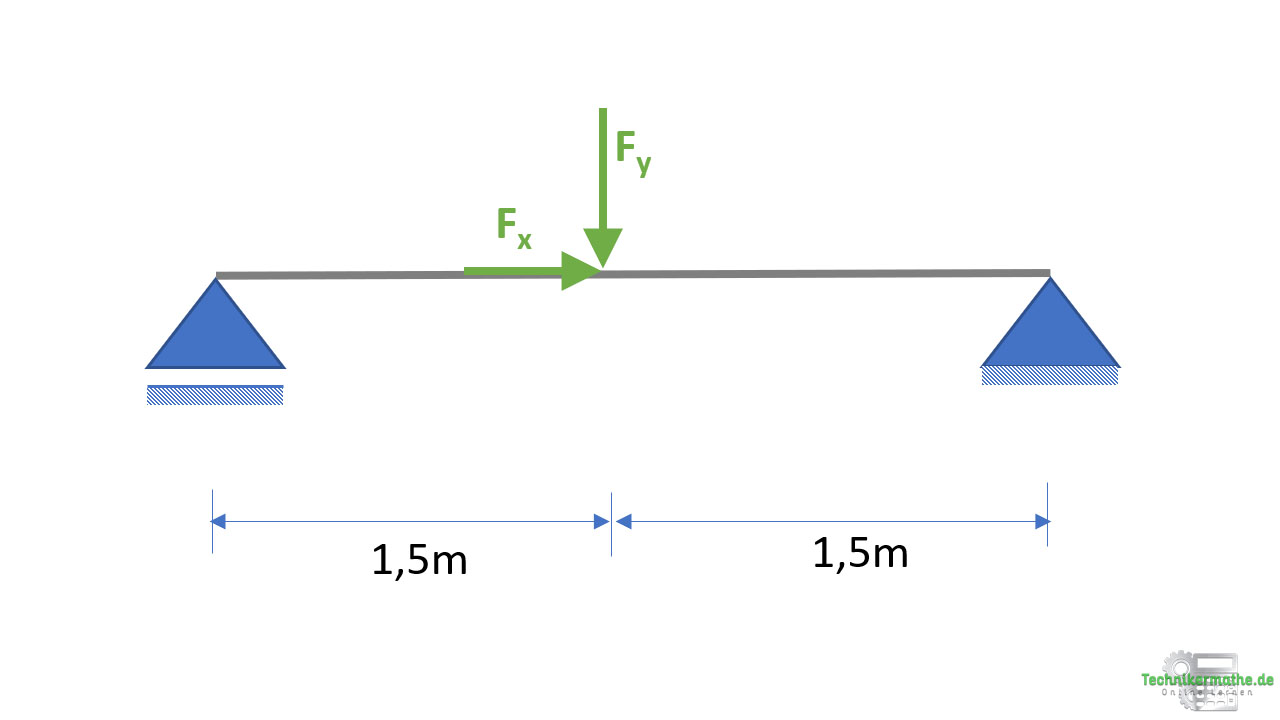
Zunächst führen wir eine Kräftezerlegung durch. Die Kraft $F$ wird mit dem Kosinus in x-Richtung und mit dem Sinus in y-Richtung zerlegt:

$F_x = F \cdot \cos(30^{\circ}) = 3 kN \cdot \cos(30^{\circ}) = 2,6 kN$

$F_y = F \cdot \sin(30^{\circ}) = 3 kN \cdot \sin(30^{\circ}) = 1,5 kN$

Auflagerkräfte berechnen

Schnittgrößen, Auflagerkräfte, Nachhilfe Techniker, Einführung Schnittgrößen, Auflagerkräfte, Freischnitt — Freischnitt: Auflagerkräfte anbringen

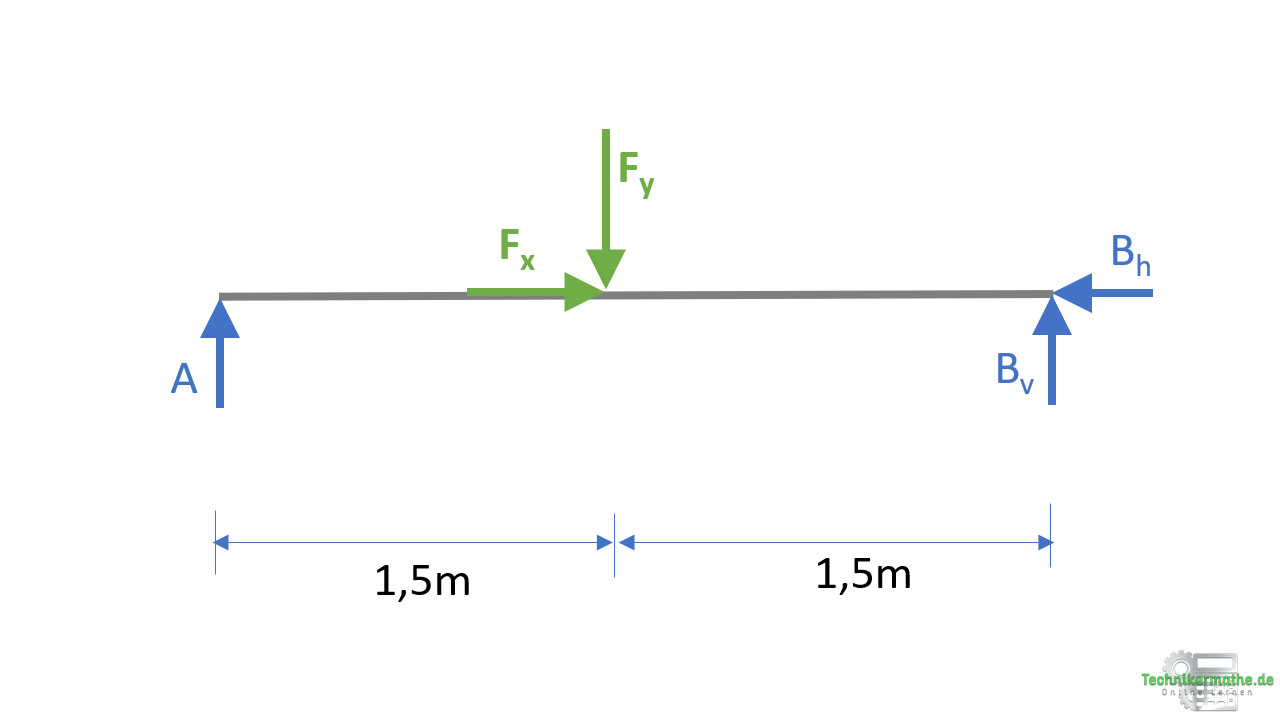
Als nächstes berechnen wir die Auflagerkräfte mittels der drei Gleichgewichtsbedingungen.

Gleichgewichtsbedingung in x-Richtung

$F_x - B_h = 0$

$B_h = F_x = 2,6 kN$

Gleichgewichtsbedingung in y-Richtung

$A -F_y + B_v = 0$

Wir haben hier zwei unbekannte Kräfte gegeben, somit müssen wir hier zunächst die Momentengleichgewichtsbedingung aufstellen.

Momentengleichgewichtsbedingung (Bezugspunkt in A)

$-F_y \cdot 1,5m + B_v \cdot 3m = 0$

$B_v = \dfrac{F_y \cdot 1,5m }{3m}$

$B_v = \dfrac{1,5 kN \cdot 1,5m }{3m} = 0,75 kN$

Aus der vertikalen Gleichgewichtsbedingung können wir als nächstes die Auflagerkraft A berechnen:

$A -F_y + B_v = 0$

$A = F_y - B_v = 1,5 kN - 0,75 kN$

$A = 0,75 kN$

Schnittgrößen bestimmen

Zur Bestimmung der Schnittgrößen müssen wir Schnitte durch den Balken durchführen. Dazu müssen wir die Schnitte so durchführen, dass zwischen den äußeren Kräfte (Auflagerkräfte, äußere Lasten) geschnitten wird. Für unser Beispiel muss zwischen dem Auflager A und der äußeren Kraft F sowie zwischen der Kraft F und dem Auflager B geschnitten werden.

Die äußere Kraft F führt dazu, dass sich die Schnittgrößen im Balken ändern. Schauen wir uns dazu die beiden Schnitte an:

Schnittgrößen, Schnitte, Nachhilfe Statik, Prüfungsvorbereitung Techniker, Einführung Schnittgrößen, Schnitte durchführen — Schnittgrößen: Schnitte angeben

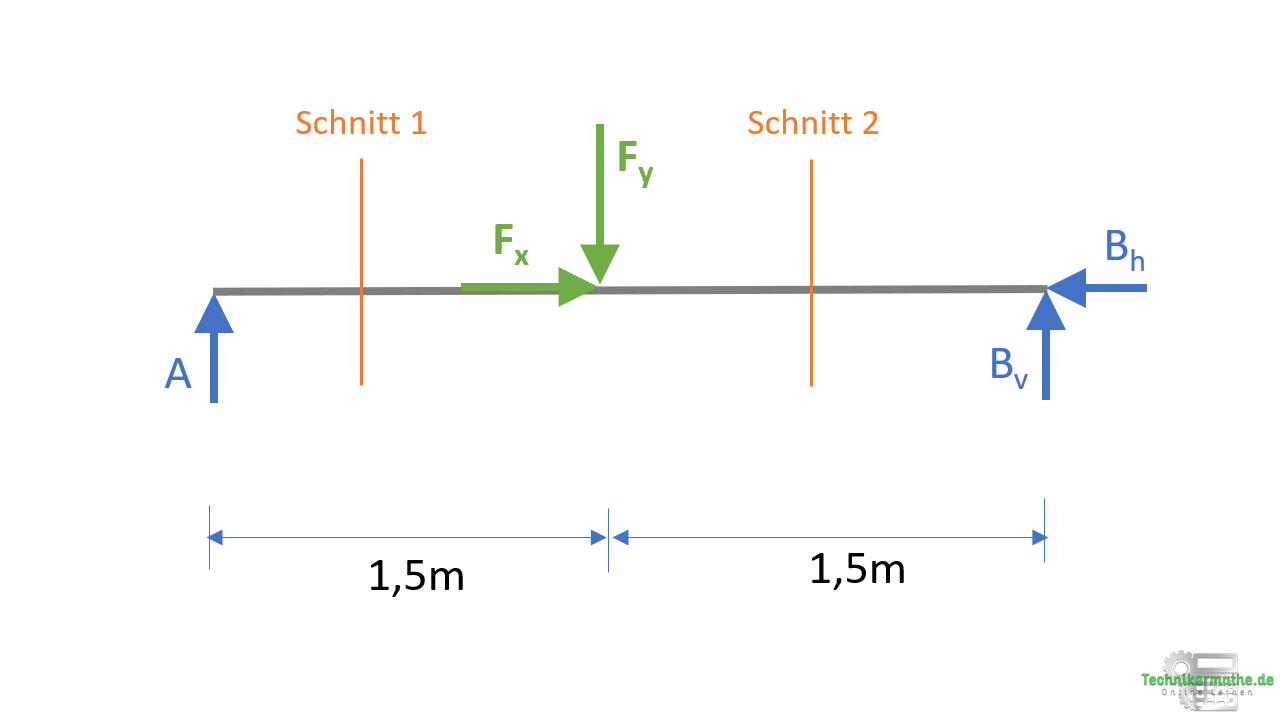
Wir können zur Berechnung der Schnittgrößen das linke oder das rechte Schnittufer betrachten. Beide Möglichkeiten führen zum selben Ergebnis. Für welches Schnittufer du dich entscheidest, bleibt dir überlassen. Es ist jedoch sinnvoll immer das Schnittufer zu wählen, an welchem weniger Kräfte angreifen, damit sich der Berechnungsaufwand verringert.

Bevor wir mit der Berechnung beginnen, legen wir zunächst eine x-Achse an den Balkenanfang. Diese x-Achse wird immer bis zum Schnitt eingezeichnet.

Schnittgrößen, x-Achse, Achse einführen, Beispiel Schnittgrößen, Einführung — Schnittgrößen: Einführung der x-Achse

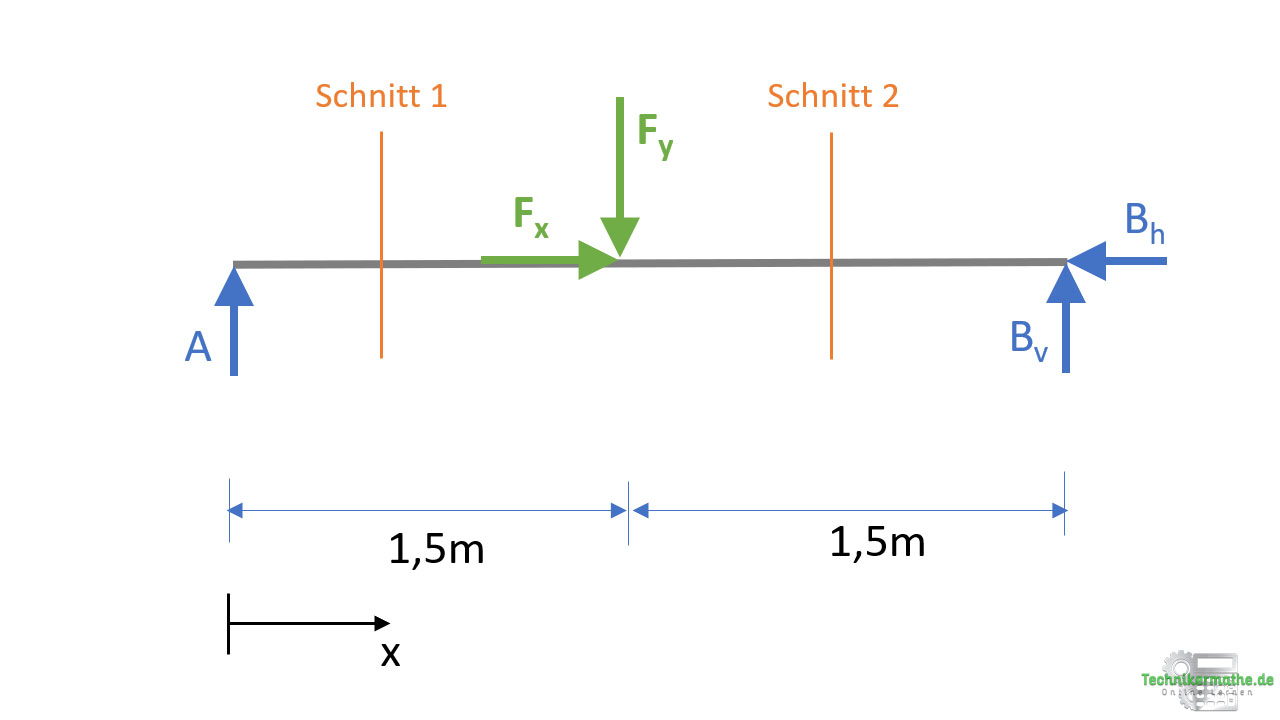
Der erste Schnitt wird zwischen 0 und 1,5 m durchgeführt. Wir betrachten das linke Schnittufer und tragen die Schnittgrößen ab.

1.Schnitt (0 ≤ x ≤ 1,5m)

Schnittgrößen: Erster Schnitt, Schnitt, Schnittgrößen, linkes Schnittufer, Einführung Schnittgrößen — Schnittgrößen: Erster Schnitt

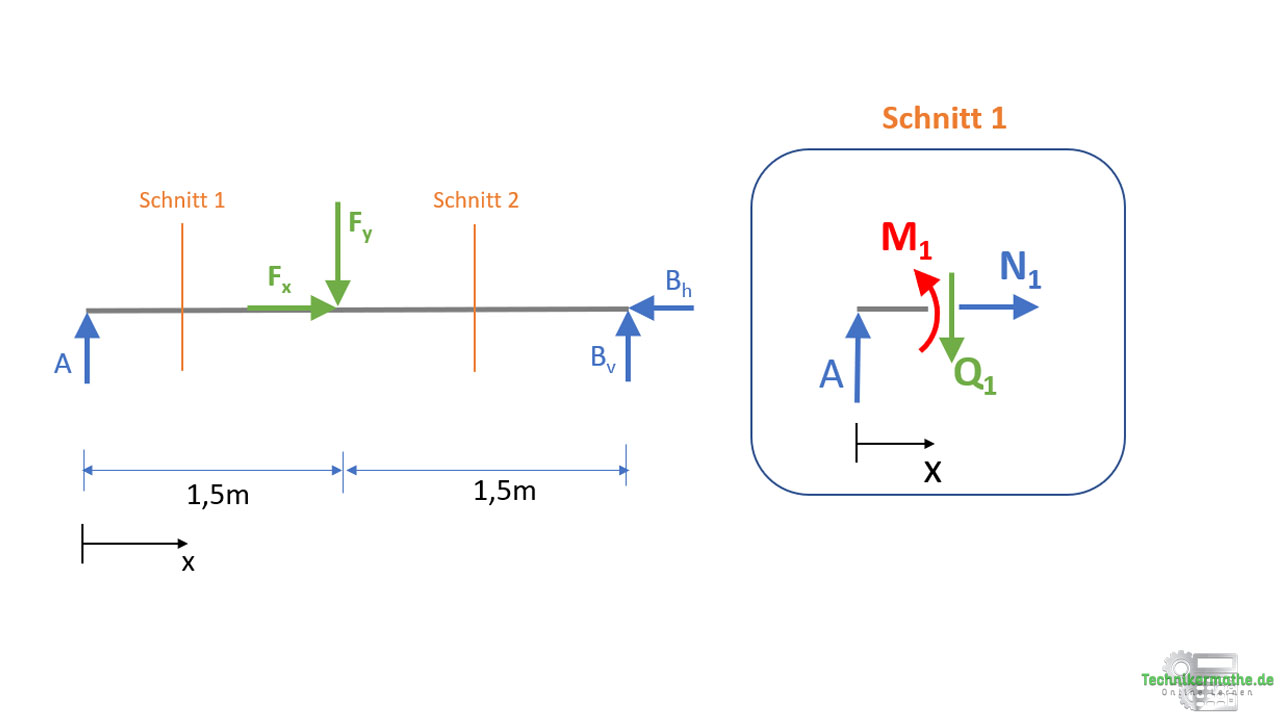
Zur Berechnung von Normalkraft, Querkraft und Moment wenden wir die Gleichgewichtsbedingungen an.

Gleichgewichtsbedingung in x-Richtung

Aus der Gleichgewichtsbedingung in x-Richtung können wir die Normalkraft N₁ berechnen:

$N_1 = 0$

Gleichgewichtsbedingung in y-Richtung

Aus der Gleichgewichtsbedingung in y-Richtung können wir die Querkraft Q₁ berechnen:

$A - Q_1 = 0$

$Q_1 = A = 0,75 kN$

Momentengleichgewichtsbedingung

Aus der Momentengleichgewichtsbedingung können wir das Biegemoment M₁ berechnen. Der Bezugspunkt liegt dabei immer im Schnitt:

$-A \cdot x + M_1 = 0$

$M_1 = A \cdot x = 0,75 kN \cdot x$

Zusammengefasst ergeben sich die folgenden Schnittgrößen für den 1. Bereich:

$N_1 = 0$

$Q_1 = 0,75 kN$

$M_1 = 0,75 kN \cdot x$

2.Schnitt (1,5m ≤ x ≤ 3m)

Schnittgrößen: Zweiter Schnitt, Schnitt, Schnittgrößen, Einführung Schnittgrößen, linkes Schnittufer — Zweiter Schnitt

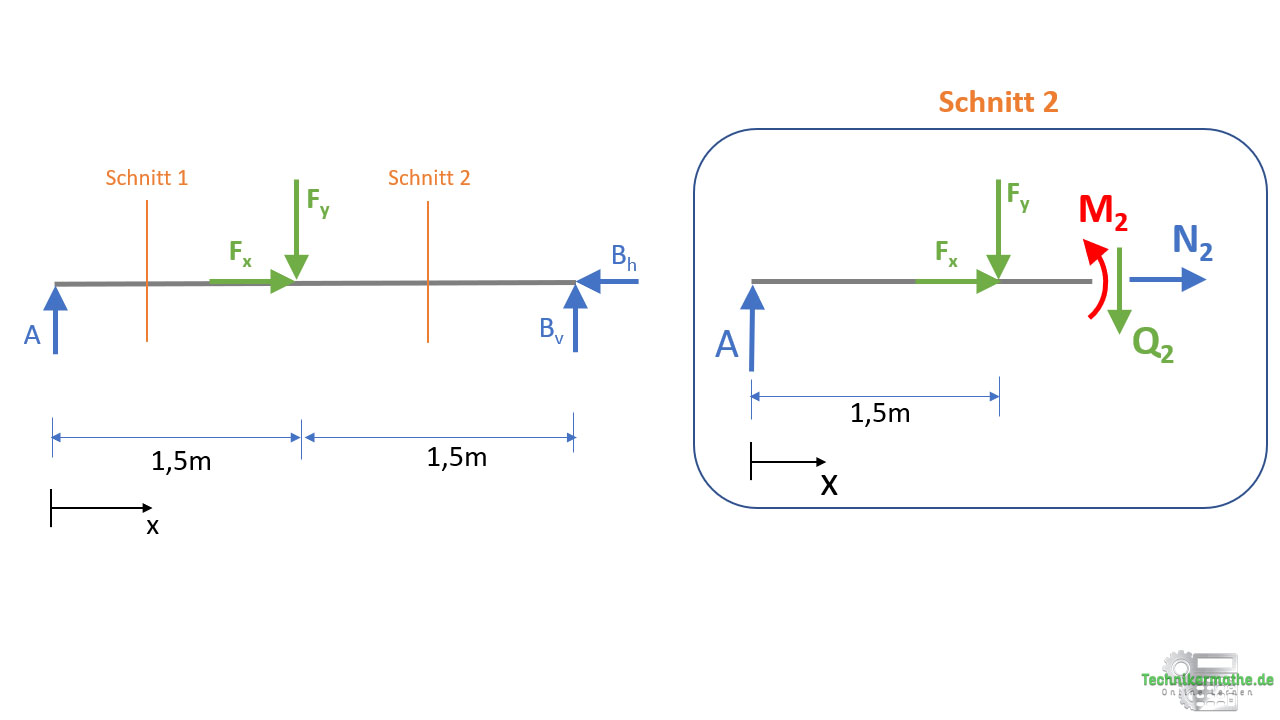
Wie betrachten auch hier wieder das linke Schnittufer und berechnen Normalkraft, Querkraft und Moment mittels der drei Gleichgewichtsbedingungen.

Gleichgewichtsbedingung in x-Richtung

Aus der Gleichgewichtsbedingung in x-Richtung können wir die Normalkraft N₂ berechnen:

$N_2 + F_x = 0$

$N_2 = -F_x = -2,6 kN$

Gleichgewichtsbedingung in x-Richtung

Aus der Gleichgewichtsbedingung in y-Richtung können wir die Querkraft Q berechnen:

$A - F_y - Q_2 = 0$

$Q_2 = A - F_y = 0,75 kN - 1,5 kN = -0,75 kN$

Momentengleichgewichtsbedingung

Aus der Momentengleichgewichtsbedingung können wir das Biegemoment M berechnen. Der Bezugspunkt liegt dabei immer im Schnitt:

$-A \cdot x + F_y \cdot (x-1,5m) + M = 0$

$M_2 = A \cdot x - F_y \cdot (x-1,5m)$

$M_2 =0,75 kN \cdot x - 1,5 kN\cdot (x-1,5m)$

$M_2 = 0,75 kN \cdot x - 1,5 kN \cdot x + 2,25 kNm$

$M_2 = -0,75 kN \cdot x + 2,25 kNm$

Zusammengefasst ergeben sich die folgenden Schnittgrößen für den 2. Bereich:

$N_2 = -2,6 kN$

$Q_2 = -0,75 kN$

$M_2 = -0,75 kN \cdot x + 2,25 kNm$

Wir haben nun alle Schnittgrößen berechnet.

Schnittgrößenverläufe einzeichnen

Die Schnittgrößen können auch grafisch dargestellt werden. Dazu werden diese in ein Koordinatensystem eingezeichnet. Normalkraft, Querkraft und Moment werden auf der y-Achse abgetragen. Die Abmessungen des Balkens auf der x-Achse.

Für das obige Beispiel ergeben sich dann die folgenden Schnittgrößenverläufe.

Normalkraftverlauf und Querkraftverlauf

Normalkraftverlauf, Querkraftverlauf, Einzelkraft, Schnittgrößenverläufe, Zustandslinien — Schnittgrößenverläufe: Normalkraftverlauf und Querkraftverlauf

In den obigen Grafiken sind die Schnittgrößenverläufe der Normalkraft und Querkraft für beide Schnittbereiche zu sehen. Der erste Schnittbereich beginnt im Koordinatenursprung und geht bis x = 1,5 (Kraftangriff von F). Der zweite Schnittbereich von x = 1,5m bis x = 3m.

Die Normalkraft N ist im ersten Schnittbereich Null, weil dort keine äußere Kraft angreift. Im zweiten Schnittbereich tritt eine konstante Normalkraft von -2,6 kN auf, weil hier die äußere Kraft F_x angreift (x-Komponente der Kraft F).

Die Querkraft Q ist im ersten Schnittbereich konstant bei 0,75 infolge der dort angreifenden Auflagerkraft und im zweiten Schnittbereich negativ bei -0,75, weil dort zusätzlich zur Auflagerkraft die äußere Kraft F_y angreift, welche der Auflagerkraft entgegenwirkt.

Momentenverlauf

Das Moment M ist im ersten Schnittbereich eine lineare Funktion mit positiver Steigung. Die Auflagerkraft A übt mit zunehmenden x ein Moment auf diesen Schnittbereich aus. Der Momentenverlauf im Schnittbereich 1 startet im Koordinatenursprung und läuft bis y = 1,125 kN. Bei einem linearen Momentenverlauf reicht es aus den Start und Endwert des Schnittbereichs in den Momentenverlauf einzusetzen und diese dann miteinander zu verbinden.

Schnittbereich 1:

Start bei x = 0:

$M_1 = 0,75 \cdot 0 = 0$

Punkt (0|0)

Ende bei x = 1,5:

$M_1 = 0,75 \cdot 1,5 = 1,125$

Punkt (1,5|1,125)

Im zweiten Schnittbereich übt zum einen die Auflagerkraft A ein Moment aus, als auch die äußere Kraft F_y. Da beide Momente entgegengesetzt zueinander sind, heben sich diese im Lager B auf. Es liegt eine lineare Funktion mit negativer Steigung vor. Diese startet bei einem Funktionswert von y = 1,125 und endet bei y = 0.

Schnittbereich 2:

Start bei x = 1,5:

$M_2 = -0,75 \cdot 1,5 + 2,25 = 1,125$

Punkt (1,5|1,125)

Ende bei x = 3:

$M_2 = -0,75 \cdot 3 + 2,25 = 0$

Punkt (3|0)

Merk’s dir!

Festlager und Loslager weisen keine Momente auf, da sie keine Momente übertragen können. Hier ist das Schnittmoment M immer Null.

Anwendung der Schnittgrößen

Statik und Festigkeitslehre: Analyse von Bauteilen und Strukturen unter Belastung.
Bauwesen: Entwurf und Überprüfung von Tragwerken wie Brücken, Gebäude und Maschinen.
Maschinenbau: Konstruktion von Bauteilen, die verschiedenen Kräften und Momenten ausgesetzt sind.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was sind Schnittgrößen?

Schnittgrößen sind interne Kräfte (Normalkraft, Querkraft) und Momente (Biegemoment) in einem Bauteil, die durch äußere Lasten verursacht werden.

2. Wie bestimme ich Schnittgrößen?

Schneide das Bauteil freihändig durch, stelle die Gleichgewichtsbedingungen auf und löse die Gleichungen für die Schnittgrößen.

3. Was ist der Unterschied zwischen Normalkraft, Querkraft und Biegemoment?

Normalkraft wirkt entlang der Längsachse, Querkraft wirkt senkrecht zur Längsachse und Biegemoment verursacht eine Biegung im Bauteil.

4. Warum sind Schnittgrößen wichtig?

Schnittgrößen sind entscheidend für die Analyse und das Design von Tragwerken und Bauteilen, um deren Festigkeit und Stabilität sicherzustellen.

5. Können Schnittgrößen variieren?

Ja, Schnittgrößen können entlang des Bauteils variieren, abhängig von der Verteilung und Art der äußeren Lasten.

Zusammenfassung

Schnittgrößen sind die internen Kräfte und Momente, die in einem Bauteil wirken, wenn es durch äußere Lasten belastet wird. Um diese zu bestimmen, wird das Bauteil freihändig geschnitten, die Gleichgewichtsbedingungen aufgestellt und die Gleichungen für die Normalkraft, Querkraft und das Biegemoment gelöst.

Schnittgrößen sind in der Statik, Festigkeitslehre, im Bauwesen und Maschinenbau von entscheidender Bedeutung, um die Stabilität und Festigkeit von Strukturen und Bauteilen sicherzustellen.

Was kommt als Nächstes?

Im nächsten Schritt befassen wir uns ausführlich mit dem Thema: Schwerpunkte berechnen

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++