TM1 – Schnittgrößen berechnen: Einzelkräfte

Wir betrachten die Berechnung von Schnittgrößen, wenn mehrere Einzellasten auf den Balken wirken. Dabei zeigen wir anhand eines ausführlichen Beispiels, wie die Lagerkräfte berechnet werden, die Schnitte durchgeführt werden und die Schnittgrößen aus den Gleichgewichtsbedingungen berechnet werden.

In dieser Lerneinheit wollen wir uns anhand eines ausführlichen Beispiels anschauen, wie du mithilfe der drei Gleichgewichtsbedingungen in der Ebene die Schnittgrößen berechnen kannst.

Für ein optimales Verständnis helfen dir ein Videoclip und ein ausführliches Rechenbeispiel zu dem Thema.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.

Wir wollen uns zunächst anschauen, wie du Schnittgrößen berechnen kannst, wenn einzelne Kräfte auf einen Balken wirken.

Vorgehensweise: Schnittgrößen berechnen

Die folgenden Vorgehensweise zur Berechnung der Schnittgrößen solltest du dir merken:

Zunächst führst du – falls notwendig – eine Kräftezerlegung durch.
Danach musst du das Bauteil freischneiden und die Auflagerkräfte abtragen.
Im nächsten Schritt berechnest du alle Auflagerkräfte.
Nach den obigen Schritten führst du einen gedanklichen Schnitt durch das Bauteil durch und trägst die drei Schnittgrößen (Normalkraft, Querkraft und Biegemoment) am linken und am rechten Schnittufer ab.
Danach wendest du die drei Gleichgewichtsbedingungen der Ebene an, um die Schnittgrößen zu berechnen.

Video: Schnittgrößen bei Einzelkräften berechnen

In dem folgenden Video zeigen wir dir, wie du die Schnittgrößen am Balken berechnen kannst.

Beispiel: Schnittgrößen bei Einzellasten berechnen

Aufgabenstellung

Schnittgrößen berechnen, Beispiel Schnittgrößen, Schnittgrößen bei Einzelkräften, Einzellast, schräge Kraft — Beispiel: Schnittgrößen bei Einzellasten

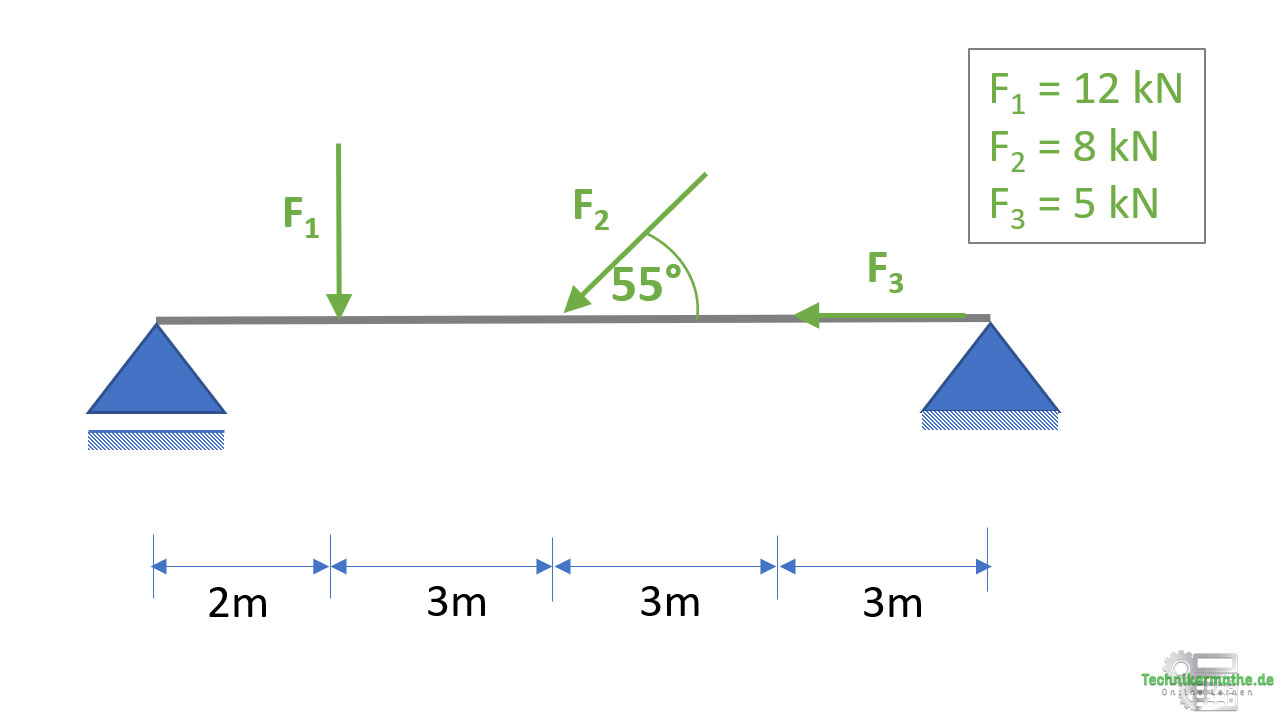
Gegeben sei der obige Balken an, welchen die drei Kräfte F₁, F₂ und F₃ angreifen. Der Balken ist im Lager A auf einem Loslager und im Lager B auf einem Festlager gelagert.

Du sollst im gesamten Balken die Schnittgrößen berechnen !

Schritt 1: Kräftezerlegung durchführen

Zunächst führen wir für alle Kräfte mit Winkel eine Kräftezerlegung durch. Die Kraft F₂ ist mit dem Winkel von 55° zur Horizontalen gegeben, demnach erhalten wir mittels Kosinus die x-Komponente und mit dem Sinus die y-Komponente:

$F_{x2} = F_2 \cdot \cos(55^{\circ}) = 8 kN \cdot \cos(55^{\circ}) = 4,59 kN$

$F_{y2} = F_2 \cdot \sin(55^{\circ}) = 8 kN \cdot \sin(55^{\circ}) = 6,55 kN$

Wir ersetzen als nächstes die Kraft F₂ durch die beiden Kraftkomponenten.

Schritt 2: Freischnitt

Als nächstes lösen wir den Balken von seinen Auflagern und tragen die Auflagerkräfte sowie die oben berechneten Kraftkomponenten an:

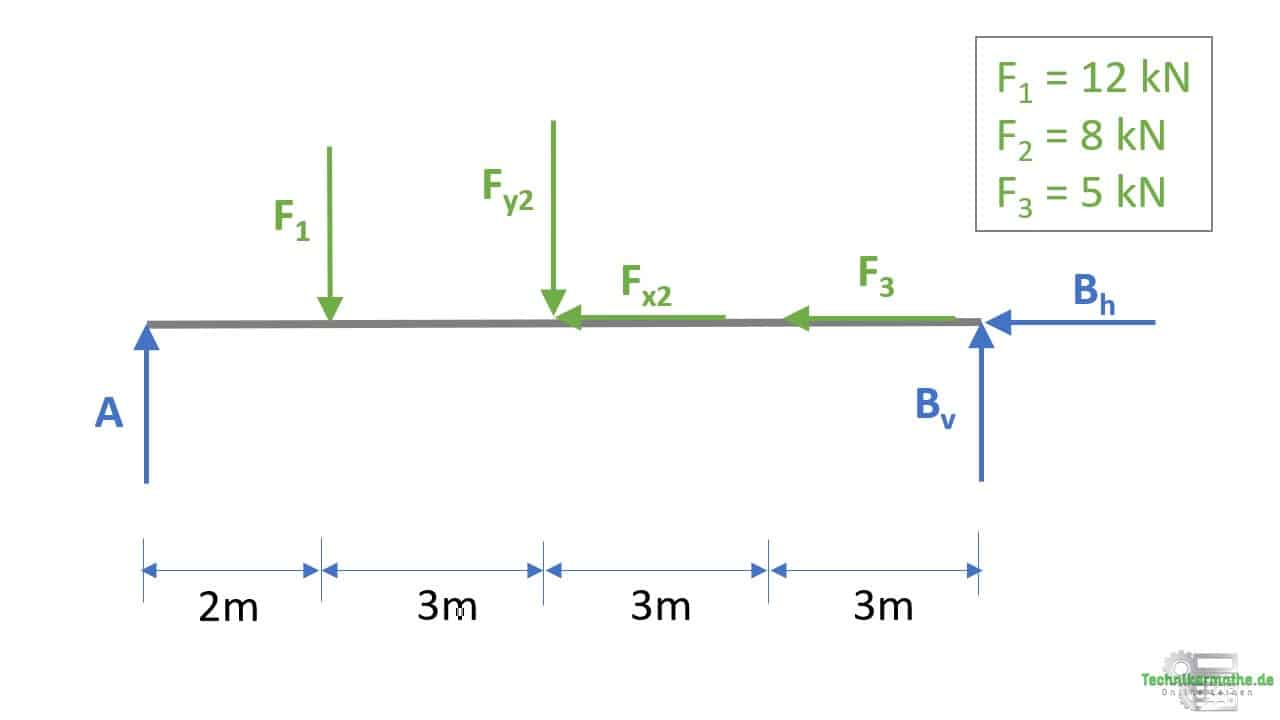
Schnittgrößen, Einzelkräfte, Kräftezerlegung, Freischnitt, Einzellasten, Schnittgrößen Einzellast — Schnittgrößen bei Einzelkräften am Balken

Schritt 3: Lagerkräfte berechnen

Als nächstes berechnen wir aus den drei Gleichgewichtsbedingungen in der Ebene die Auflagerkräfte.

Gleichgewichtsbedingung in x-Richtung

$\sum F_{ix} = 0$ :

$-F_{x2} - F_3 - B_h = 0$

Auflösen nach der unbekannten Auflagerkraft B_h und einsetzen der gegebenen Werte:

$B_h = -F_{x2} - F_3$

$B_h = -4,59 kN - 5 kN$

$B_h = -9,59 kN$

Gleichgewichtsbedingung in y-Richtung

$\sum F_{iy} = 0$ :

$A - F_1 -F_{y2} + B_v = 0$

Wir können hier noch keine Auflagerkraft bestimmen, da zwei unbekannte Auflagerkräfte gegeben sind. Wir betrachten also zunächst die Momentengleichgewichtsbedingung.

Momentengleichgewichtsbedingung

Wir legen den Bezugspunkt so, dass eine der noch unbekannten Auflagerkräfte aus der Berechnung herausfällt. Wir wählen hier beliebig das Lager A aus. Alle Kräfte bzw. Wirkungslinien die das Lager A bereits schneiden weisen keinen Hebelarm auf und werden somit innerhalb der Momentengleichgewichtsbedingung nicht berücksichtigt, da diese Kräfte kein Moment auf das Lager A ausüben. Hierzu gehören A, F_x2, F₃, B_h.

$\sum M_i^A = 0:$

$-F_1 \cdot 2m - F_{y2} \cdot 5m + B_v \cdot 11m = 0$

Wir lösen die obige Gleichung nach Bv auf und setzen die gegebenen Werte ein:

$B_v = \dfrac{F_1 \cdot 2m + F_{y2} \cdot 5m}{11m}$

$B_v = \dfrac{12 kN \cdot 2m + 6,55 kN \cdot 5m}{11m}$

$B_v = 5,16 kN$

Wir können nun aus der Gleichgewichtsbedingung in y-Richtung die Auflagerkraft A bestimmen:

$A - F_1 -F_{x2} + B_v = 0$

$A = F_1 + F_{x2} - B_v$

$A = 12 kN + 6,55 kN - 5,16 kN$

$A = 13,39 kN$

Es sind nun alle Auflagerkräfte bestimmt. Wir können als nächstes damit beginnen die Schnittgrößen im Balken zu berechnen.

Auflagerkraft	A	B_h	B_v
Betrag	13,39 kN	-9,59 kN	5,16 kN

Schritt 4: Schnittgrößen bei Einzellasten

Wir wollen uns nun ausführlich anschauen, wie du die Schnittgrößen bei Einzellasten berechnest.

Jede Kraft bzw. jedes Moment am Balken führt zu inneren Kräfte. Damit ändern sich die inneren Kräfte (Schnittgrößen), wenn eine Kraft oder ein Moment an den Balken angreift. Um nun die Schnittgrößen für den obigen Balken bestimmen zu können, schneidest du diesen immer zwischen den Kräften. Sind Momente gegeben, so wird auch zwischen Momenten bzw. zwischen Kraft und Moment geschnitten. Kräfte bzw. Momente sind alle äußeren Kräfte bzw. Momente sowie alle Auflagerkräfte bzw. -momente. Ein Schnitt erfolgt nie durch eine Kraft.

Merk’s dir!

Wir können zur Berechnung der Schnittgrößen das linke oder rechte Schnittufer verwenden. Beide Schnittufer führen zum selben Ergebnis. Wir wählen immer das Schnittufer mit der geringsten Anzahl an Kräften, damit die Berechnungen schneller durchgeführt werden können.

Natürlich kannst du auch bei einem Schnittufer verbleiben, wenn es für dich einfacher ist.

In der folgenden Grafik siehst du die Anzahl an Schnitten die wir durchführen müssen:

Schnittgrößen: Schnitte festlegen, Schnitte, Balken, Schnittgrößen bei Einzellasten, Schnittgrößen bei Einzelkräften — Schnittgrößen: Schnitte festlegen

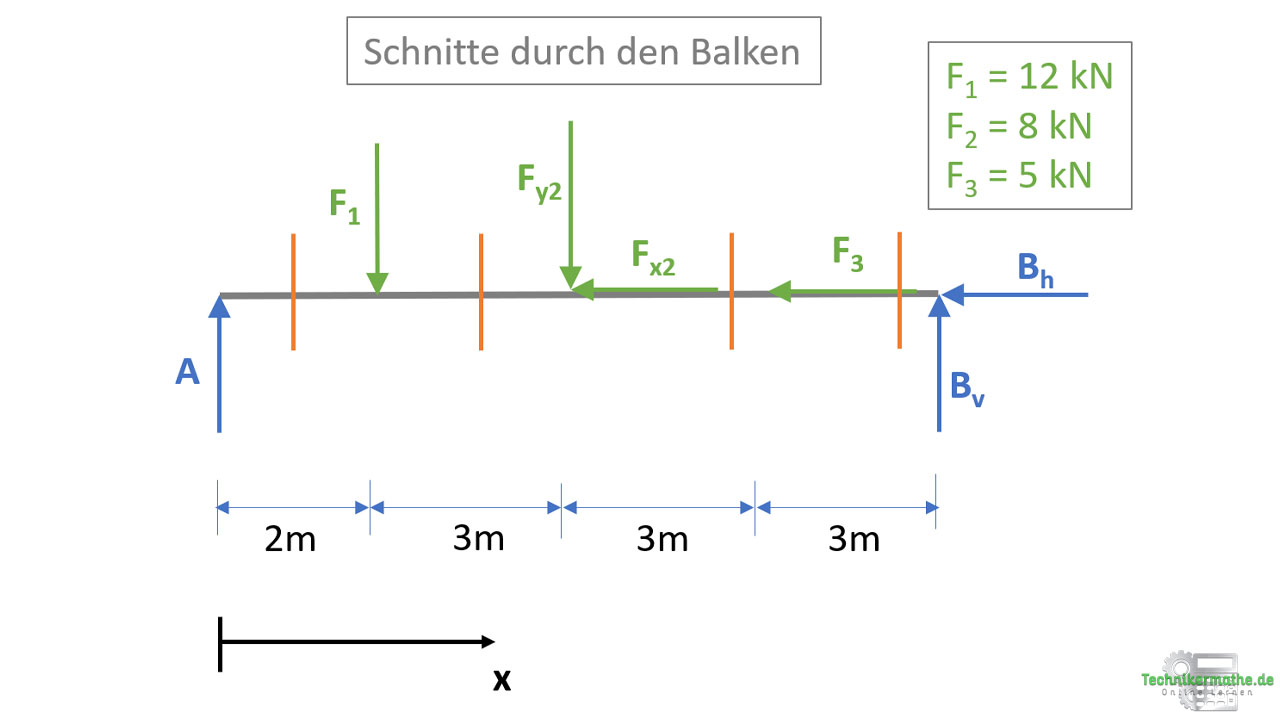
Du siehst oben die vier Schnitte, die wir durchführen müssen. Die Schnitten werden immer zwischen den Kräften durchgeführt (nie durch eine Kraft). Die x-Achse legst du an den Balkenanfang.

Wir betrachten im Folgenden jeden Schnitt separat und wollen für jeden Schnittbereich die Schnittgrößen berechnen.

Schnitt 1: 0 ≤ x ≤ 2m

Wir betrachten zunächst den ersten Schnitt und wollen hier die Schnittgrößen in diesem Bereich (0 ≤ x ≤ 2m) berechnen. In der folgenden Grafik haben wir dazu einen Schnitt zwischen der Auflagekraft A und F₁ durchgeführt und betrachten das linke Schnittufer:

Schnittgrößen berechnen, Schnittgrößen bei Einzellasten, Einzelkräfte, linkes Schnittufer — Schnittgrößen bei Einzellasten: 1. Schnitt

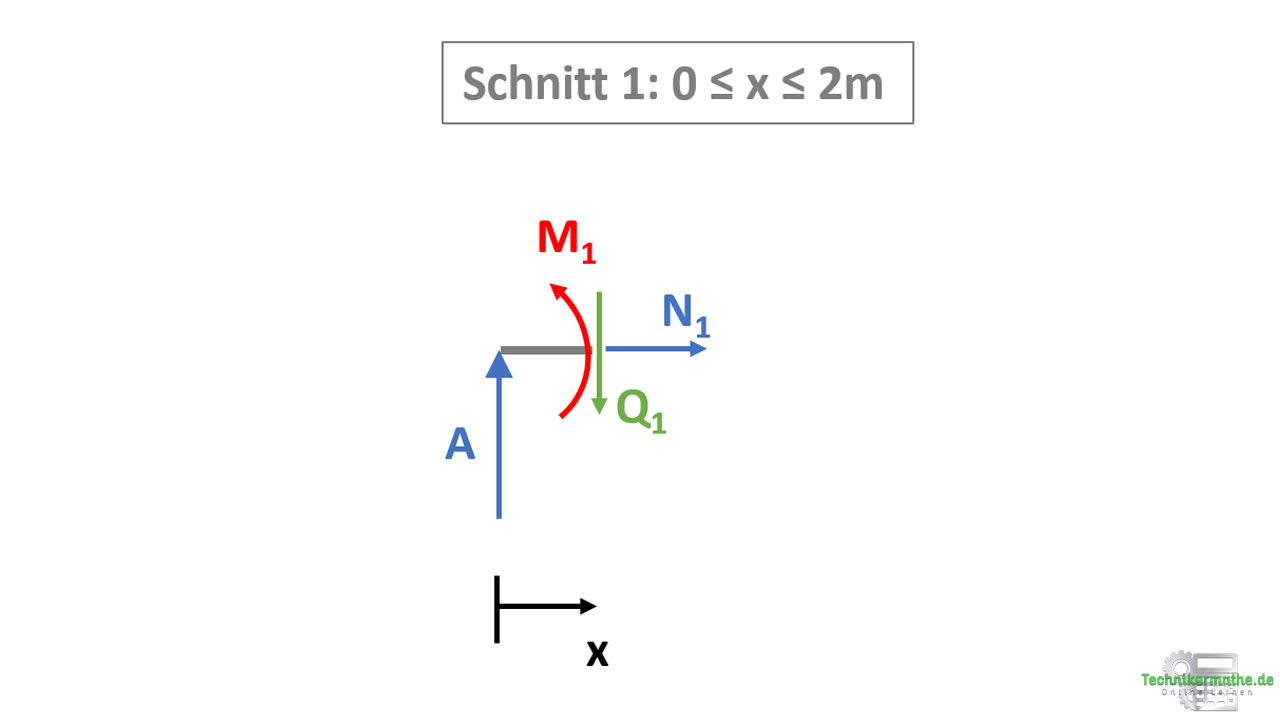
Wir wenden zunächst die horizontale Gleichgewichtsbedingung an, um die Normalkraft N zu berechnen:

$\sum F_{ix} = 0$ :

$N_1 = 0$

Da keine horizontale Kraft in diesem Bereich angreift, ist hier die Normalkraft im Balken gleich Null.

Danach betrachten wir die vertikale Gleichgewichtsbedingung, um die Querkraft Q zu berechnen:

$\sum F_{iy} = 0$ :

$A - Q_1 = 0$

$Q_1 = A$

$Q_1 = 13,39 kN$

Aus der vertikalen Gleichgewichtsbedingung erhalten wir Q_1 = 13,39 kN. Im Bereich 0 ≤ x ≤ 2m ist die Querkraft konstant.

Mittels der Momentengleichgewichtsbedingung können wir nun das Biegemoment M berechnen. Bei der Bestimmung der Schnittgrößen liegt der Bezugspunkt immer im Schnitt, d.h. Normalkraft und Querkraft fallen aus der Berechnung heraus.

$\sum M_i = 0$ :

$M_1 - A \cdot x = 0$

$M_1 = A \cdot x$

$M_1 = 13,39 kN \cdot x$

Momente werden innerhalb der Momentengleichgewichtsbedingung gemäß ihres Drehsinns berücksichtigt (positiv bei Linksdrehenden, negativ bei rechtsdrehenden Momenten). Das Biegemoment M ist am linken Schnittufer ein Linksdrehendes, weshalb wir dieses positiv berücksichtigen.

Außerdem weist die Auflagerkraft A einen senkrechten Abstand zum Bezugspunkt (Schnitt) auf. Dieser beträgt $x$ , ist also abhängig davon, wo wir genau den Balken schneiden. Wollen wir also wissen, wie groß das Biegemoment M im Balken bei x=1m ausfällt, dann können wir in die obige Gleichung x = 1m einsetzen und erhalten:

$M_1 = 13,39 kN \cdot 1m = 13,39 kNm$ Biegemoment M bei x = 1

Das Biegemoment M wird mit zunehmendem x größer. Die obige Gleichung gilt nur für den ersten Bereich 0 ≤ x ≤ 2m.

Schnitt 2: 2m ≤ x ≤ 5m

Schnittgrößen bei Einzellasten, Schnitte, Schnittgrößen, Beispiel, linkes Schnittufer — Schnittgrößen bei Einzellasten: Schnitt 2

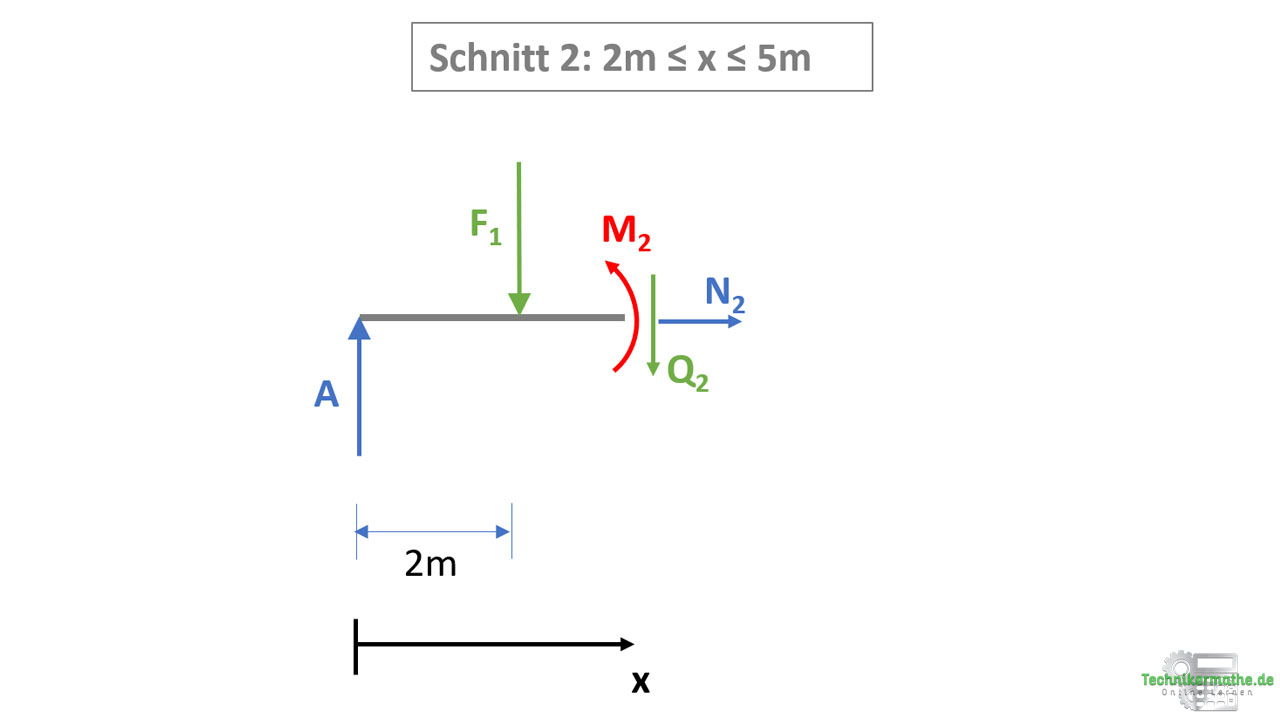
Wir führen einen Schnitt zwischen der Kraft F₁ und der Kraft F₂ bzw. der Kraftkomponenten durch und betrachten wieder das linke Schnittufer. Wir wenden nun nacheinander die drei Gleichgewichtsbedingungen in der Ebene an, um die Schnittgrößen zu bestimmen.

Merk’s dir!

Die x-Achse wird wieder bis zum Schnitt gezogen (hier bis zum Schnittbereich 2). Die Abmessungen der davorliegenden Schnittbereiche werden mit angegeben. Diese benötigen wir für die Berechnung des Moments.

Horizontale Gleichgewichtsbedingung

$\sum F_{ix} = 0$ :

$N_2 = 0$

Vertikale Gleichgewichtsbedingung

$\sum F_{iy} = 0$ :

$A - F_1 - Q_2 = 0$

$Q_2 = A - F_1 = 13,39 kN - 12 kN$

$Q_2 = 1,39 kN$

Die negative Querkraft sagt aus, dass diese genau entgegengesetzt zur angenommenen Richtung wirkt, also vertikal nach oben.

Momentengleichgewichtsbedingung

Der Bezugspunkt liegt wieder im Schnitt, so dass Querkraft und Normalkraft bei der Berechnung herausfallen:

$\sum M_i = 0$ :

$M_2 - A \cdot x + F_1 (x - 2m)= 0$

Lagerkraft A übt ein rechtsdrehendes Moment auf den Schnitt aus, die Kraft F₁ ein linksdrehendes Moment. Dazu stell dir den Teilbalken im Schnitt fixiert vor und überlege dir, in welche Richtung die betrachtete Kraft den Teilbalken um den Schnitt dreht.

Der Hebelarm der Lagerkraft A beträgt x, weil diese am Balkenanfang liegt. Die Kraft F₁ startet auf der x-Achse erst bei x = 2m, weshalb diese von x abgezogen werden muss:

Schnittgrößen, Hebelarm, Schnittgrößen bei Einzelkräften — Schnittgrößen bei Einzelkräften: Hebelarm

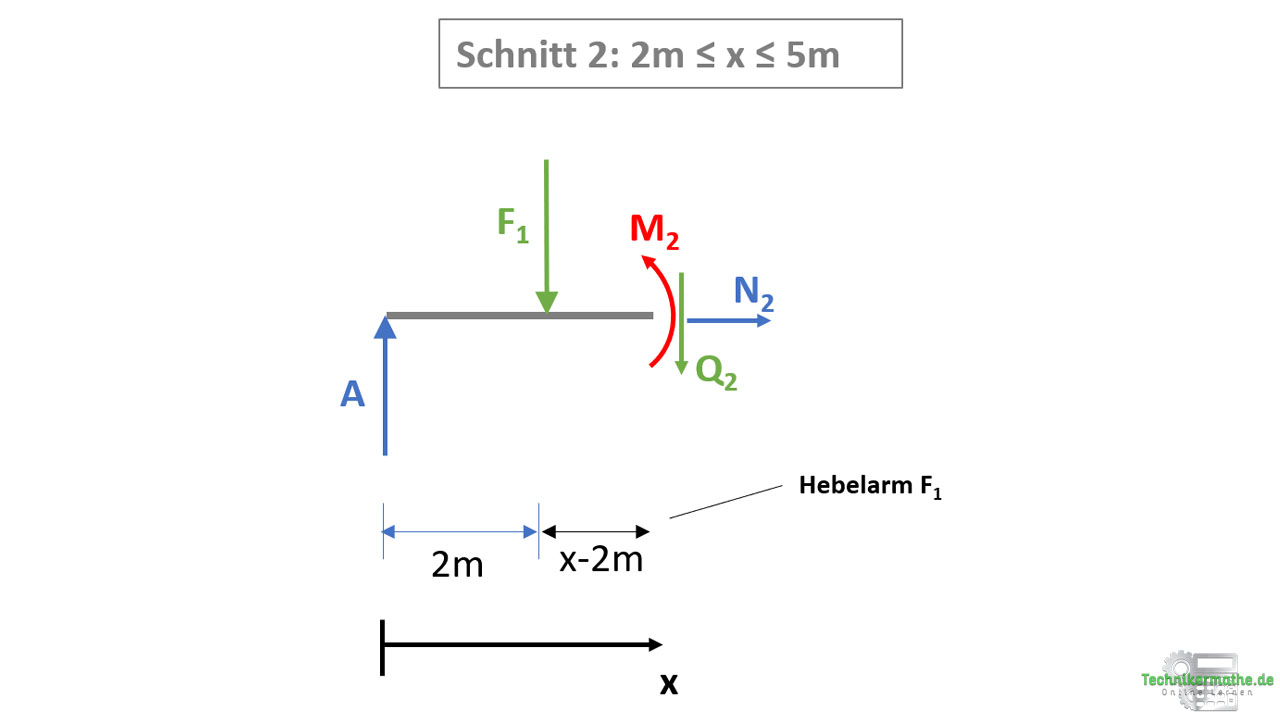
Wir lösen als nächstes die obige Gleichung nach M₂ auf, setzen die gegebenen Werte ein, lösen die Klammern auf und fassen zusammen:

$M_2 = A \cdot x - F_1(x-2m) =$

$M_2 = 13,39 kN \cdot x -12 kN (x - 2m)$

$M_2 = 13,39 kN \cdot x -12 kN \cdot x + 24 kNm$

$M_2 = 1,39 kN \cdot x + 24 kNm$

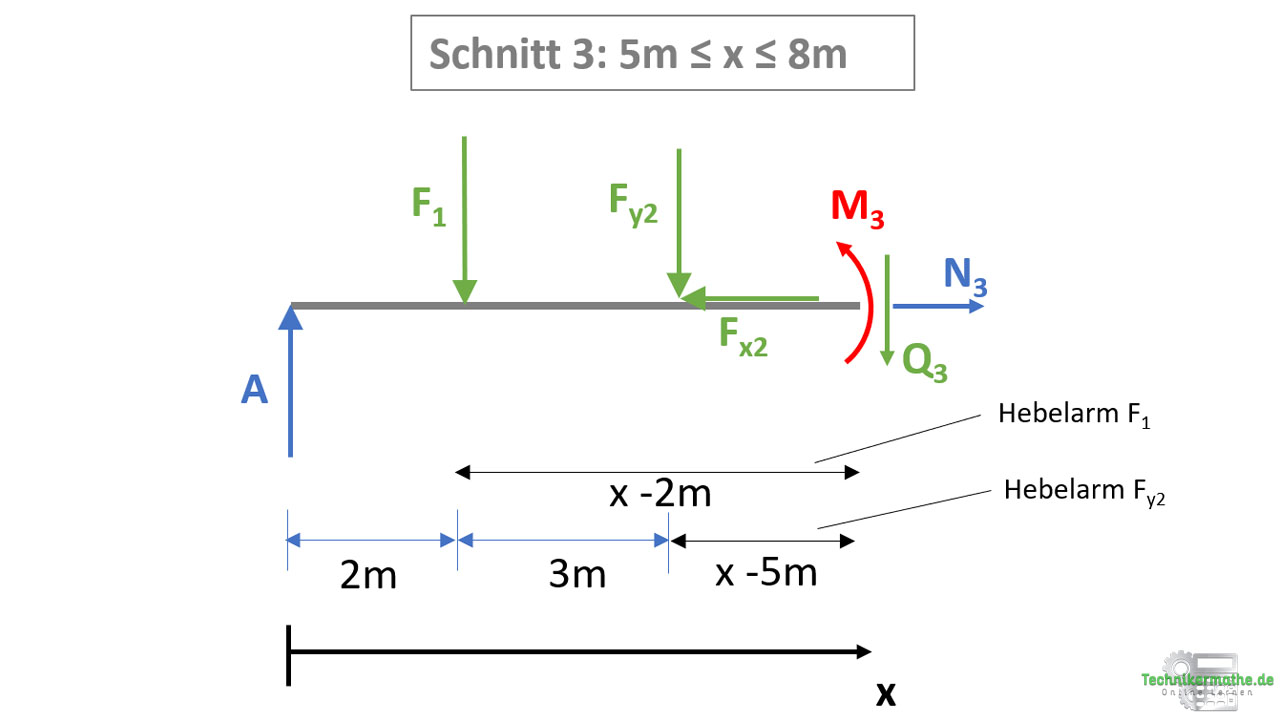
Schnitt 3: 5m ≤ x ≤ 8m

Schnittgrößen, Einzellasten, Einzelkräfte, linkes Schnittufer, Schnittufer — Schnittgrößen bei Einzellasten: Schnitt 3

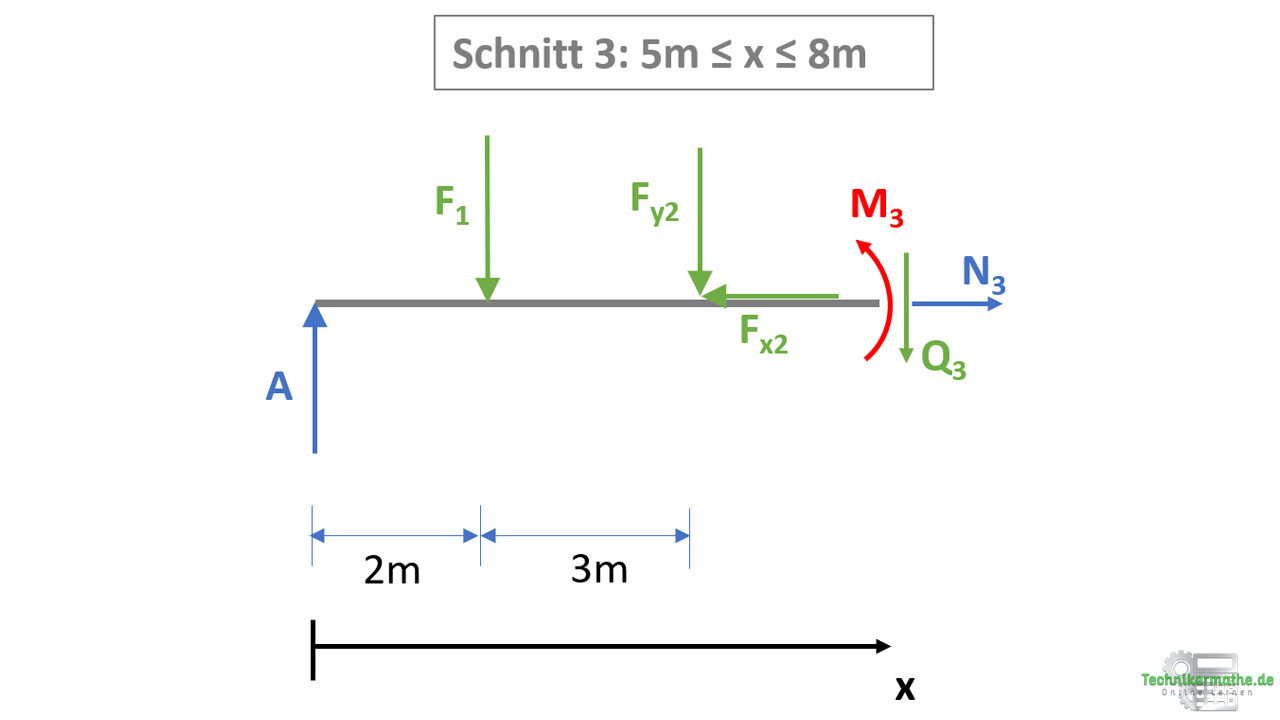
Wir führen einen Schnitt zwischen der Kraft F₂ bzw. ihren Kraftkomponenten und der Kraft F₃ durch und betrachten wieder das linke Schnittufer. Wir wenden nun nacheinander die drei Gleichgewichtsbedingungen in der Ebene an, um die Schnittgrößen zu bestimmen.

Merk’s dir!

Die x-Achse wird wieder bis zum Schnitt gezogen (hier bis zum Schnittbereich 3). Die Abmessungen der davorliegenden Schnittbereiche werden mit angegeben. Diese benötigen wir für die Berechnung des Moments.

Horizontale Gleichgewichtsbedingung

$\sum F_{ix} = 0$ :

$N_3 - F_{x2} = 0$

$N_3 = F_{x2}$

$N_3 = 4,59 kN$

Vertikale Gleichgewichtsbedingung

$\sum F_{iy} = 0$ :

$A - F_1 - F_{y2} - Q_3 = 0$

$Q_3 = A - F_1 - F_{y2} = 13,39 kN - 12 kN - 6,55 kN$

$Q_3 = -5,16 kN$

Die negative Querkraft sagt aus, dass diese genau entgegengesetzt zur angenommenen Richtung wirkt, also vertikal nach oben.

Momentengleichgewichtsbedingung

$\sum M_i = 0$ :

$M_3 - A \cdot x + F_1 (x - 2m) + F_{y2} (x - 5m) = 0$

Lagerkraft A übt ein rechtsdrehendes Moment auf den Schnitt aus, die Kraft F₁ und F_y2 ein linksdrehendes Moment. Die Wirkungslinie der Kraft Fx2 schneidet den Schnitt, deswegen besitzt diese keinen senkrechten Abstand und damit kein Moment.

Der Hebelarm der Lagerkraft A beträgt x, weil diese am Balkenanfang liegt. Die Kraft F₁ startet auf der x-Achse erst bei x = 2m, weshalb diese von x abgezogen werden muss. Die Kraft Fy2 startet bei x = 5m, weshalb der Hebelarm x-5m beträgt:

Schnittgrößen, Einzelkräfte, Einzellasten, Hebelarm, Schnittufer — Schnittgrößen bei Einzelkräften: Hebelarm

Wir lösen als nächstes die obige Gleichung nach M₃ auf, setzen die gegebenen Werte ein, lösen die Klammern auf und fassen zusammen:

$M_3 = A \cdot x - F_1(x-2m) - F_{y2} (x - 5m)$

$M_3 = 13,39 kN \cdot x - 12 kN (x - 2m) - 6,55 kN (x - 5m)$

$M_3 = 13,39 kN \cdot x -12 kN \cdot x + 24 kNm - 6,55 kN \cdot x + 32,75 kNm$

$M_3 = -5,16 kN \cdot x + 56,75 kNm$

Als nächsten betrachten wir den vierten und letzten Schnittbereich, für welchen wir die Schnittgrößen berechnen wollen.

Schnitt 4: 8m ≤ x ≤ 11m

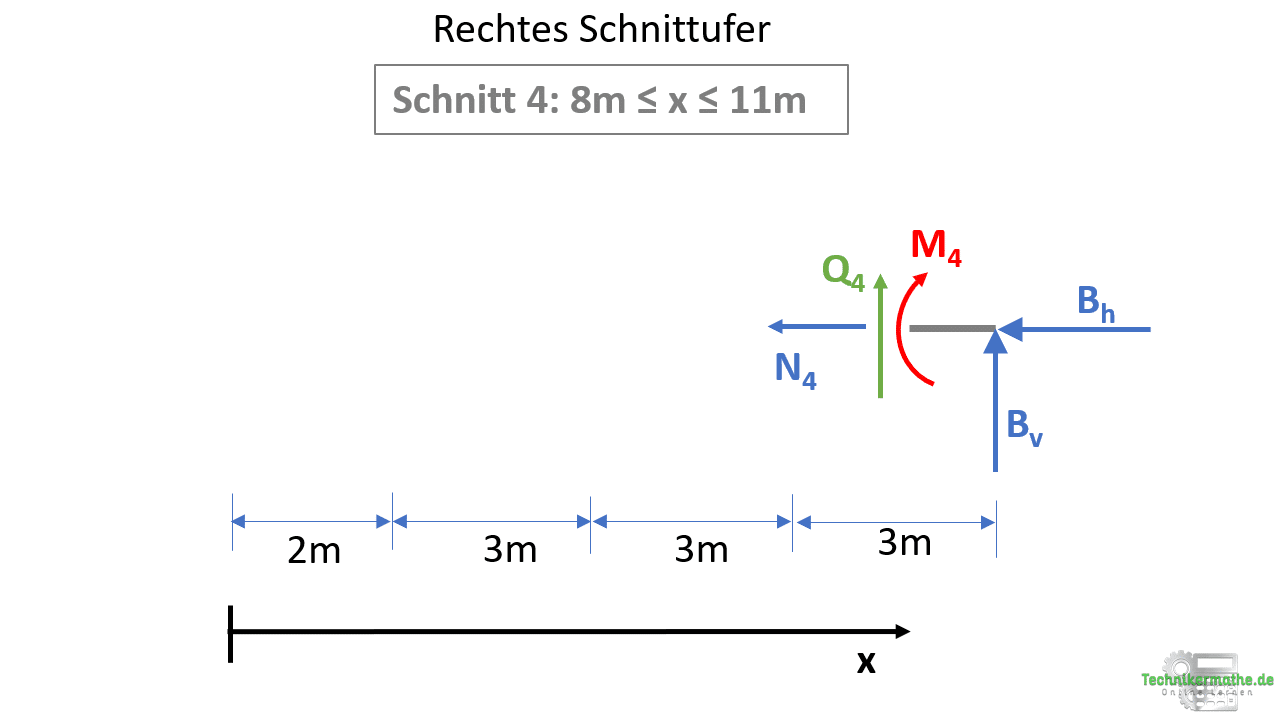
Schnittgrößen bestimmen, Einzelkräfte, rechtes Schnittufer — Schnittgrößen bei Einzellasten: Schnitt 4 (rechtes Schnittufer)

Wir wollen uns hier mal das rechte Schnittufer anschauen. Wir können natürlich ebenfalls das linke Schnittufer betrachten, allerdings fällt die Berechnung am rechten Schnittufer kürzer aus, weil hier weniger Kräfte am rechten Balkenteil gegeben sind. Der Schnitt wird hier zwischen der Kraft F₃ und der Lagerkraft B durchgeführt.

Die Schnittgrößen sind hier genau entgegengesetzt abzutragen. Die Normalkraft zeigt also nach links, die Querkraft nach oben und das Biegemoment ist rechtsdrehend.

Merk’s dir!

Die x-Achse wird wieder bis zum Schnitt gezogen. Wenn wir das rechte Schnittufer betrachten, dann benötigen wir trotzdem die Abmessungen der Schnittbereiche, die gerade nicht betrachtet werden.

Horizontale Gleichgewichtsbedingung

$\sum F_{ix} = 0$ :

$-N_4 - B_h = 0$

$N_4 = -B_h$

$N_4 = -(-9,59 kN) = 9,59 kN$

Vertikale Gleichgewichtsbedingung

$\sum F_{iy} = 0$ :

$B_v + Q_4 = 0$

$Q_4 = -B_v$

$Q_4 = -5,16 kN$

Die negative Querkraft sagt aus, dass diese genau entgegengesetzt zur angenommenen Richtung wirkt, also vertikal nach unten.

Momentengleichgewichtsbedingung

$\sum M_i = 0$ :

$-M_4 + B_v \cdot (11m - x) = 0$

Das Biegemoment ist am rechten Schnittufer ein rechtsdrehendes Moment und wird somit negativ berücksichtigt. Die Kraft B_v weist einen senkrechten Abstand zum Schnitt auf und liegt am Balkenende bei x = 11m. Demnach ist der Hebelarm in diesem Fall 11m – x (die x-Achse reicht bis zum Schnitt). Die Kraft B_v übt ein linksdrehendes Moment auf den Schnitt aus.

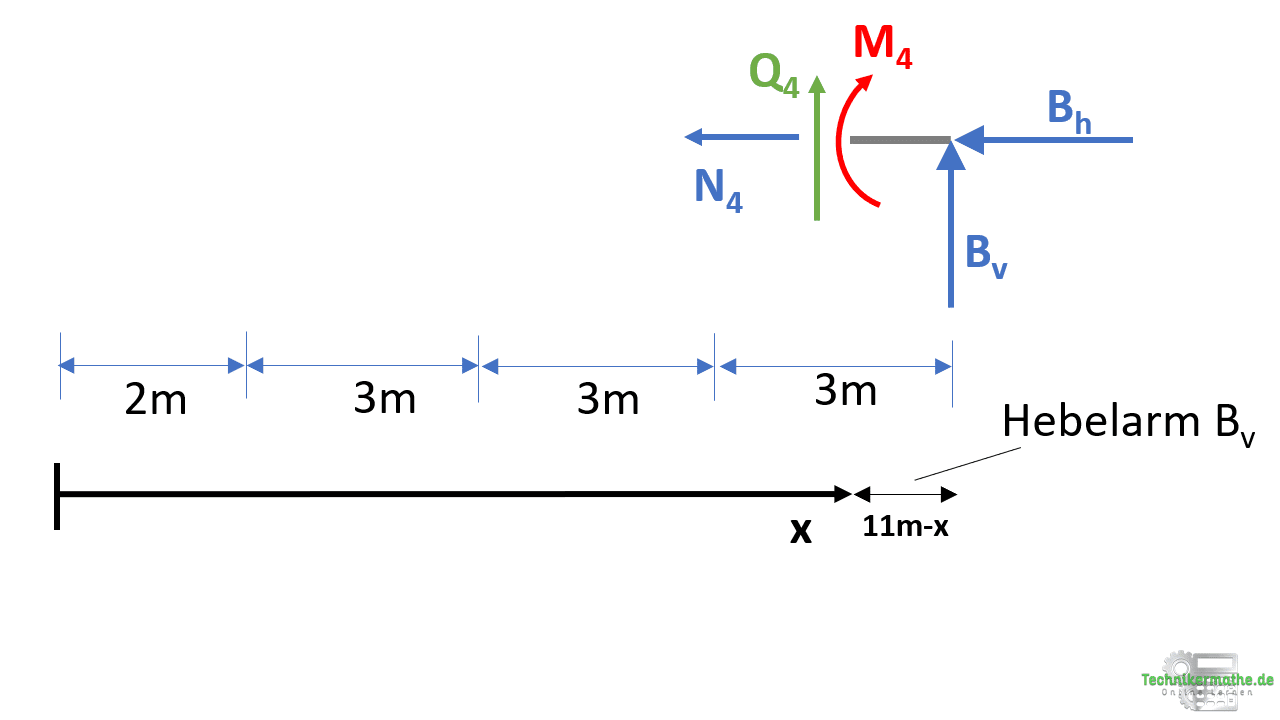
Schnittgrößen, Hebelarm, Momentenverlauf, rechtes Schnittufer — Schnittgrößen bei Einzelkräften: Hebelarm

Wir lösen als nächstes die obige Gleichung nach M₄ auf, setzen die gegebenen Werte ein, lösen die Klammern auf und fassen zusammen:

$M_4 = B_v \cdot (11m - x)$

$M_4 = 5,16 kN \cdot (11m - x)$

$M_4 = 56,76 kNm - 5,16 kN \cdot x$

$M_4 = - 5,16 kN \cdot x + 56,76 kNm$

Wir haben alle Schnittgrößen für die einzelnen Schnittbereiche bestimmt.

Willst du nun zum Beispiel wissen, welche Schnittgrößen im Balken bei x = 6m wirken, dann betrachtest du den 3. Schnittbereich (5m ≤ x ≤ 8m).

$N_3 = 4,59 kN$

$Q_3 = -5,16 kN$

$M_3 = -5,16 kN \cdot x + 56,75 kNm$ |x = 6m einsetzen

$M_3 = -5,16 kN \cdot 6m + 56,75 kNm = 25,79 kNm$

In der folgenden Lerneinheit schauen wir uns mal an, wie du Schnittgrößen berechnen kannst, wenn eine rechteckige Streckenlast gegeben ist.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++