TM1 – Grafische Vektoraddition (Resultierende)

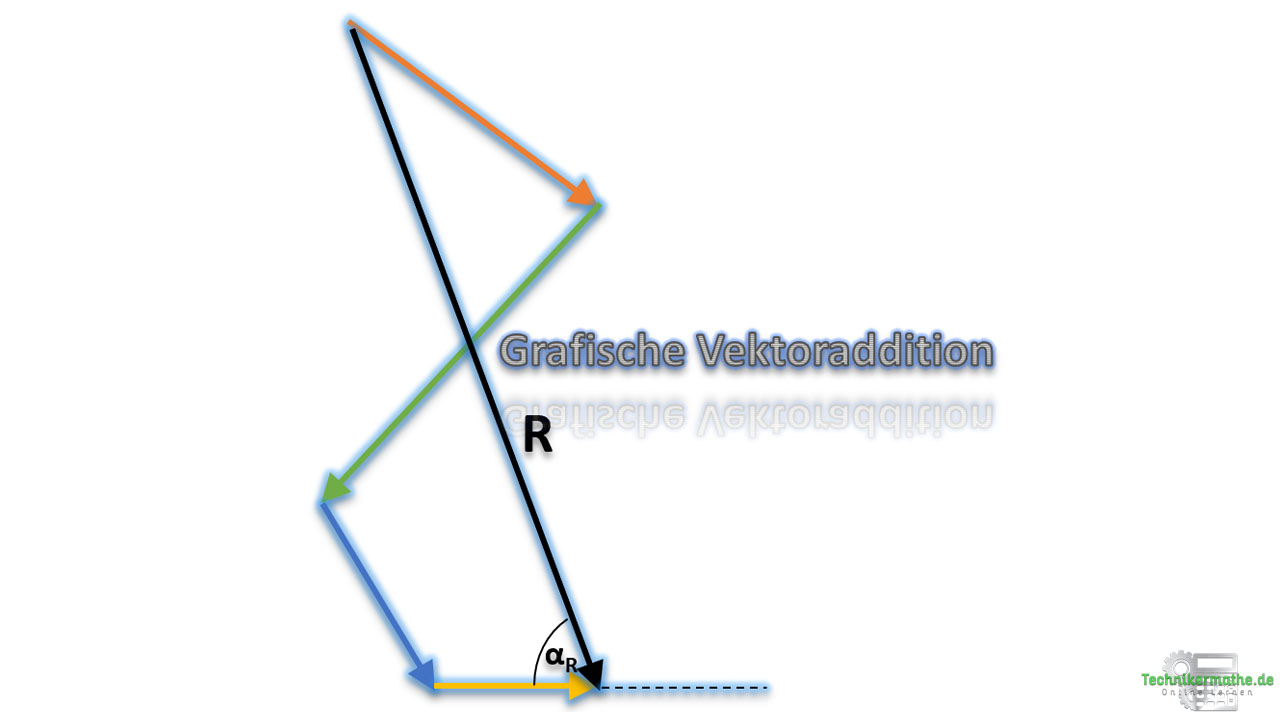
Die grafische Vektoraddition ist die Aneinanderreihung von Kraftvektoren in einer beliebigen Reihenfolge. Ziel ist die grafische Ermittlung der Resultierenden. Mittels grafischer Vektoraddition kann nur der Betrag und die Richtung der Resultierenden bestimmt werden, nicht aber die Lage der Resultierenden.

Eine resultierende Kraft R oder F_R ist die Zusammenfassung mehrerer Kräfte zu einer einzigen Kraft. Diese Kraft hat dann dieselbe Wirkung auf den betrachteten Körper, wie die einzelnen Kräfte zusammen.

In dieser Lerneinheit schauen wir uns die grafische Vektoraddition an und zeigen dir, wie du die Resultierende (Betrag und Richtung) aus mehreren Kräften berechnen kannst.

Für ein optimales Verständnis helfen dir ein Videoclip und ein ausführliches Beispiel zur grafischen Vektoraddition.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.

Die Berechnung einer resultierenden Kraft kennst du bereits aus den vorangegangenen Lerneinheiten. Wir wollen dir in dieser Lerneinheit zeigen, wie du mithilfe der grafischen Vektoraddition den Betrag und die Richtung der resultierenden Kraft grafische ermitteln kannst.

Merk’s dir!

Für die Anwendung der grafischen Vektoraddition muss die Größe der einzelnen Kräfte bzw. die Längen ihrer Kraftpfeile gegeben sein sowie die Wirkungslinien und Richtungen der Kräfte.

Für ein allgemeines Kräftesystem gilt: Mittels grafischer Vektoraddition kann nur der Betrag und die Richtung der Resultierenden bestimmt werden, nicht aber die Lage der Resultierenden. Dafür wird das Seileckverfahren (folgende Lerneinheit) herangezogen. Betrachtest du hingegen ein zentrales Kräftesystem, so liegt die Resultierende im gemeinsamen Angriffspunkt der Kräfte.

Schauen wir uns die Ermittlung der resultierenden Kraft mittels grafischer Vektoraddition mal an einem Beispiel an.

Beispiel: Grafische Vektoraddition – Resultierende bestimmen

Grafische Vektoraddition, Beispiel, Resultierende, Vektoraddition, Balken — Beispiel: Grafische Vektoraddition

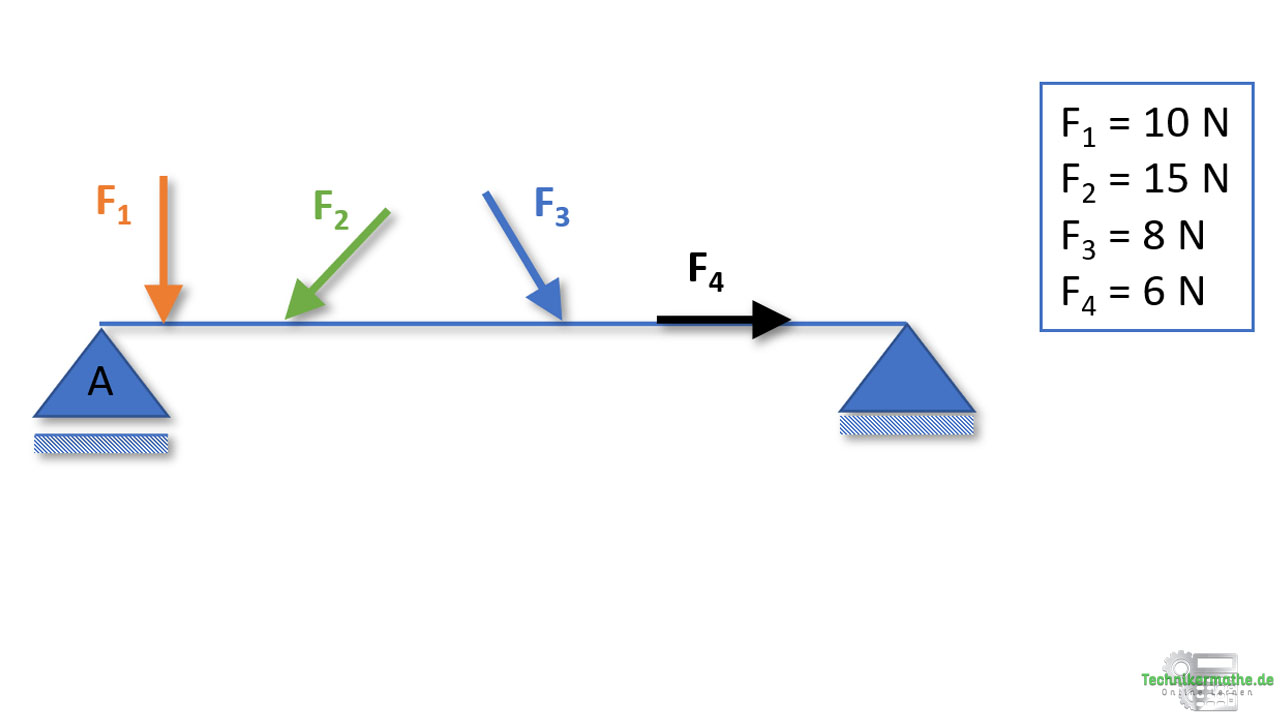
Gegeben sei der obige Balken, welcher durch die 4 äußeren Kräfte belastet wird. Diese 4 Kräfte sollen nun zu einer Resultierenden zusammengefasst werden. Wir wollen hier den Betrag und die Richtung dieser berechnen.

Schritt 1: Maßstab festlegen

Im ersten Schritt müssen wir einen geeigneten Maßstab festlegen. Diesen wählst du so, dass du alle Kräfte möglichst genau auf ein Zeichenblatt zeichnen kannst. Denk daran, dass die obigen Kräfte aneinandergereiht werden müssen, so dass eine größere Figur entsteht (z.B. 1 N = 2cm). Für diesen Fall werden dann alle Kräfte entsprechend einzeichnet:

$F_1 = 5cm$

$F_2 = 7,5 cm$

$F_3 = 4 cm$

$F_4 = 3cm$

Schritt 2: Grafische Vektoraddition durchführen

Du kannst nun damit beginnen die Kräfte aneinander zu reihen. Dazu gehst du wie folgt vor:

Du beginnst mit einer beliebigen Kraft und zeichnest diese dem gewählten Maßstab entsprechend ein. Danach wählst du die nächste Kraft (beliebig) und legst diese mit ihrem Anfangspunkt an die Spitze der vorangegangenen Kraft. Diese Schritte führst du solange aus, bis du alle Kräfte einmal berücksichtigt hast. Die Reihenfolge der Kräfte ist dabei beliebig wählbar.

In der folgenden Grafik siehst du, wie die grafische Vektoraddition funktioniert:

Grafische Vektoraddition, Beispiel, Vektoraddition, Resultierende, mehrere Kräfte — Grafische Vektoraddition mehrerer Kräfte

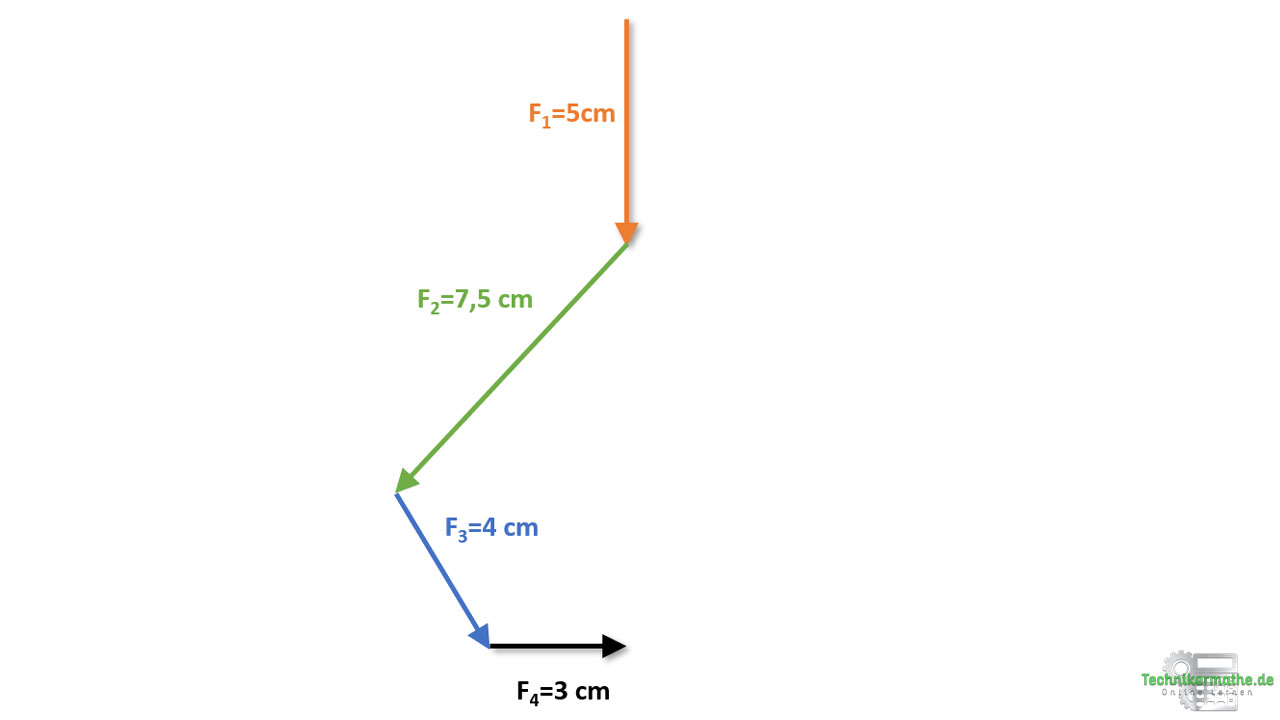
Wir haben die Kräfte F₁ bis F₄ gemäß grafischer Vektoraddition aneinandergereiht. Dabei sind wir chronologisch vorgegangen. Es ergibt sich damit das obige Bild.

Schritt 3: Resultierende ermitteln

Wir wollen als nächstes den Betrag und die Richtung der resultierenden Kraft bestimmen. Dazu gehen wir wie folgt vor:

Der Anfangspunkt der resultierenden Kraft wird an den Anfangspunkt der zuerst gewählten Kraft (hier F₁) und die Spitze der resultierenden Kraft an die Spitze der zuletzt gewählten Kraft (hier F₄).

In der folgenden Grafik siehst du, wie die Resultierende bestimmt wird:

Grafische Vektoraddition, Resultierende, mehrere Kräfte, Vektoraddition, Beispiel — Grafische Vektoraddition: Bestimmung der Resultierenden

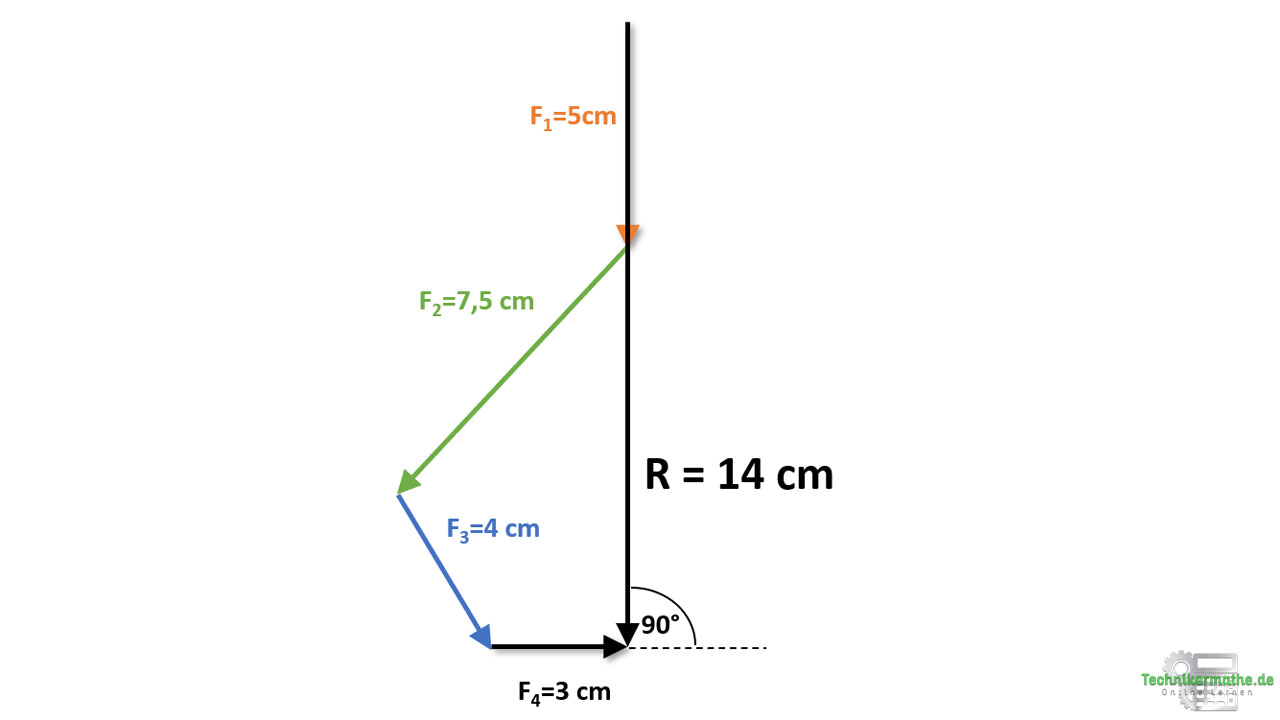
In der obigen Grafik haben wir die resultierende Kraft eingezeichnet. Sie liegt mit ihrem Anfangspunkt am Anfangspunkt der Kraft F₁ und mit ihrer Spitze an der Spitze der Kraft F₄.

Um den Betrag der Resultierenden zu bestimmen, kannst du ganz einfach mittels Geodreieck die Länge der Resultierenden messen. In unserem Beispiel weist diese eine ungefähre Länge von 14cm auf. Dies entspricht (nach Umrechnung mittels Maßstab) einem Betrag von 28 Newton.

Die Richtung der resultierenden Kraft bestimmst du, indem du den Winkel dieser zur Horizontalen ermittelst. In unserem Beispiel ergibt sich eine vertikal gerichtete resultierende Kraft, die demnach einen Winkel von 90° zur Horizontalen aufweist.

Schritt 4: Probe mittels analytischer Berechnung

Ob du richtig gezeichnet hast, kannst du dann rechnerisch ermitteln. Dazu benötigst du die Winkel der einzelnen Kräfte zur Horizontalen (F₂ und F₃), diese kannst du einfach abmessen. In unserem Beispiel weisen die Winkel α₂ = 46,6° und α₃ = 59° auf.

Analytische Berechnung von Betrag und Richtung der resultierenden Kraft findest du zum Beispiel in der vorangegangenen Lerneinheit dieses Kurses Resultierende im allgemeinen Kräftesystem.

Teilresultierende in x-Richtung

$R_x = -F_2 \cdot \cos(45,6^{\circ}) + F_3 \cdot \cos(59^{\circ}) + F_4$

$R_x = -15 N \cdot \cos(45,6^{\circ}) + 8 N \cdot \cos(59^{\circ}) + 6 N = -0,37 N$

Teilresultierende in y-Richtung

$R_y = -F_1 - F_2 \cdot \sin(45,6^{\circ}) - F_3 \cdot \sin(59^{\circ})$

$R_y = -10 N - 15 N \cdot \sin(45,6^{\circ}) - 8 N \cdot \sin(59^{\circ}) = -27,57 N$

Resultierende bestimmen

$R = \sqrt{R_x^2 + R_y^2} = \sqrt{(-0,37 N)^2 + (-27,57 N)^2} = 27,57 N$

Der gemessene Betrag von 28 Newton mittels grafischer Lösung ist sehr nah dran am tatsächlichen Ergebnis von 27,57 Newton.

Richtung der resultierenden Kraft

$\tan(\alpha_R) = \dfrac{R_y}{R_x}$

Auflösen nach α:

$\alpha_R =\tan^{-1} (\dfrac{R_y}{R_x})$

$\alpha_R =\tan^{-1} (\dfrac{-27,57 N}{-0,37 N})$

$\alpha_R = 89,23^{\circ}$

Wir haben zeichnerisch einen 90°-Winkel zur Horizontalen ermittelt und demnach eine vertikal gerichtete Kraft. Tatsächlich weist die Resultierende einen Winkel von 89,23° zur Horizontalen auf und ist demnach nicht genau vertikal gerichtet. Die Zeichnung ist aber sehr nah am Ergebnis dran.

Grafische Vektoraddition:

Zunächst legst du einen geeigneten Maßstab für den Betrag der Kräfte fest.
Danach führst du die grafische Vektoraddition durch, indem du die Kräfte gemäß des gewählten Maßstabs aneinander reihst. Die Richtung der Kräfte darfst du dabei nicht verändern.
Zum Schluss fügst du die resultierende Kraft ein und misst Länge sowie Winkel zur Horizontalen.

Video: Grafische Vektoraddition – Resultierende

Im folgenden Video betrachten wir die grafische Vektoraddition zur Bestimmung der resultierenden Kraft.

Was kommt als Nächstes?

Nachdem du weißt, wie die grafische Vektoraddition funktioniert, können wir als nächstes das Seileckverfahren zur grafischen Bestimmung der Lage der resultierenden Kraft betrachten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++