Ein grafisches Kräftegleichgewicht ist dann gegeben, wenn die Aneinanderreihung der Kraftvektoren (=grafische Vektoraddition) ein geschlossenes Krafteck bzw. geschlossenes Kräftepolygon ergeben.
Für ein optimales Verständnis helfen dir ein Videoclip und zwei anschauliche Rechenbeispiele zum zwei und drei Kräftegleichgewicht.
Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.
In dieser Lerneinheit schauen wir uns ein grafisches Kräftegleichgewicht, wenn zwei bzw. drei Kräften gegeben sind.
Wir betrachten zunächst zwei Kräfte, die sich im Gleichgewicht miteinander befinden.
Grafisches Kräftegleichgewicht – Zwei-Kräfte-Gleichgewicht
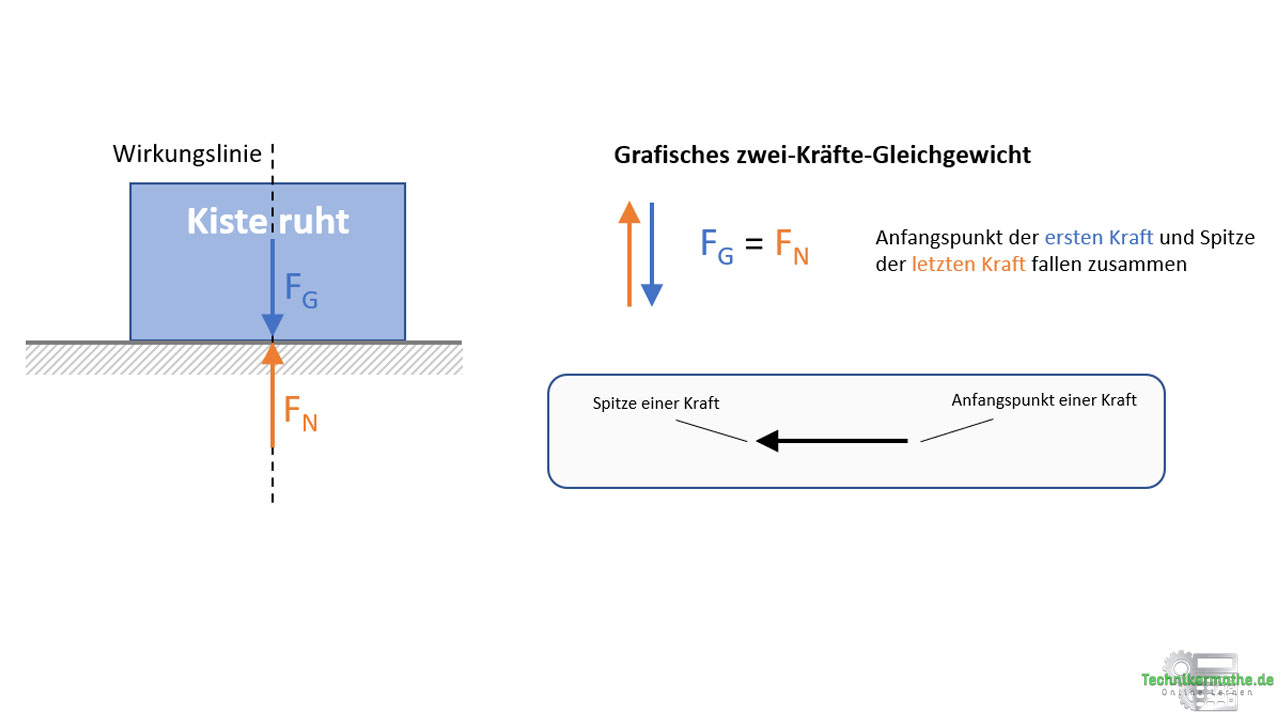
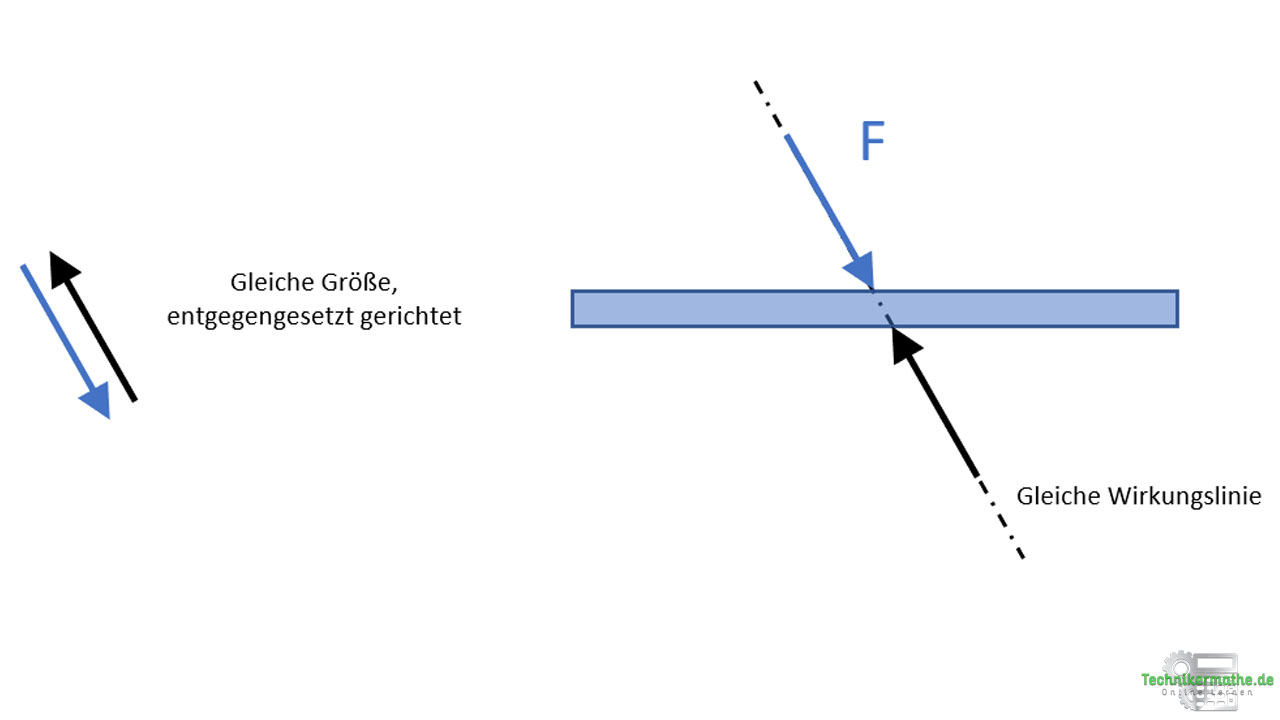
In der obigen Grafik ist eine Kiste mit einer gewissen Masse m gegeben. Aufgrund der Masse der Kiste und der Erdanziehung besitzt diese die Gewichtskraft FG, die vertikal nach unten gerichtet ist. Die horizontale Ebene übt ebenfalls eine Kraft auf die Kiste aus, die Normalkraft FN. Die Kiste befindet sich in Ruhe, demnach müssen sich auch die beiden Kräfte im Gleichgewicht befinden.
Da wir uns innerhalb der Statik befinden und ruhende Körper betrachten, befinden sich alle auf den Körper wirkenden Kräfte im Gleichgewicht, d.h. die Summe aller Kräfte ist gleich Null. Die beiden Kräfte FG und FN sind nur dann im Gleichgewicht, wenn sie die gleiche Größe (FG = FN ) aufweisen, auf der selben Wirkungslinie liegen, aber ihre Richtung genau entgegengesetzt ist.
Im obigen Fall weisen beide Kräfte die gleiche Größe auf, liegen auf einer Wirkungslinien und sind genau entgegengesetzt zueinander gerichtet.
Zwei Kräfte, die an einem Körper angreifen, sind im Kräftegleichgewicht, wenn sie
- den gleichen Betrag und
- die gleiche Wirkungslinie aber
- die entgegengesetzte Richtung besitzen.
In einem solchen Fall heben sich die Kräfte gegenseitig auf (sie “kompensieren sich”). Betrachten wir die grafische Vektoraddition so ist im Fall eines Kräftegleichgewichts die resultierende Kraft gleich Null.
Grafisches Kräftegleichgewicht: Vektoraddition
Im obige Fall haben wir die beiden Kräfte FN und FG mithilfe der grafischen Vektoraddition aneinander gereiht. Zunächst haben wir die Kraft FG eingezeichnet, danach die Kraft FN und zwar so, dass diese mit dem Anfangspunkt an die Spitze der Kraft FG gelegt wird.
Wenn dann der Anfangspunkt der ersten Kraft und die Spitze der letzten Kraft zusammenfallen, so ist ein Kräftegleichgewicht gegeben. Die grafische Vektoraddition kann für eine beliebige Anzahl an Kräften durchgeführt werden.
Dieses Vorgehen gilt auch für mehr als zwei Kräfte (die grafische Vektoraddition zur Bestimmung der Resultierenden haben wir bereits behandelt).
Video: Grafisches Kräftegleichgewicht (Vektoraddition)
In diesem Video zeigen wir dir, wie eine grafische Vektoraddition bei einem Kräftegleichgewicht funktioniert.
Als nächstes betrachten wir drei nicht parallele Kräfte die sich im Gleichgewicht miteinander befinden.
Grafisches Kräftegleichgewicht: Drei-Kräfte-Gleichgewicht
Ein drei-Kräfte-Gleichgewicht ist dann gegeben, wenn auf einen Körper drei Kräfte wirken und sich der Körper im Gleichgewicht befindet, also ruht. Auch in diesem Fall können die drei auf den Körper wirkenden Kräfte mittels grafischer Vektoraddition (siehe obige Merke-Box) aneinander gereiht werden.
Schauen wir uns dazu mal die nachfolgende Grafik an:
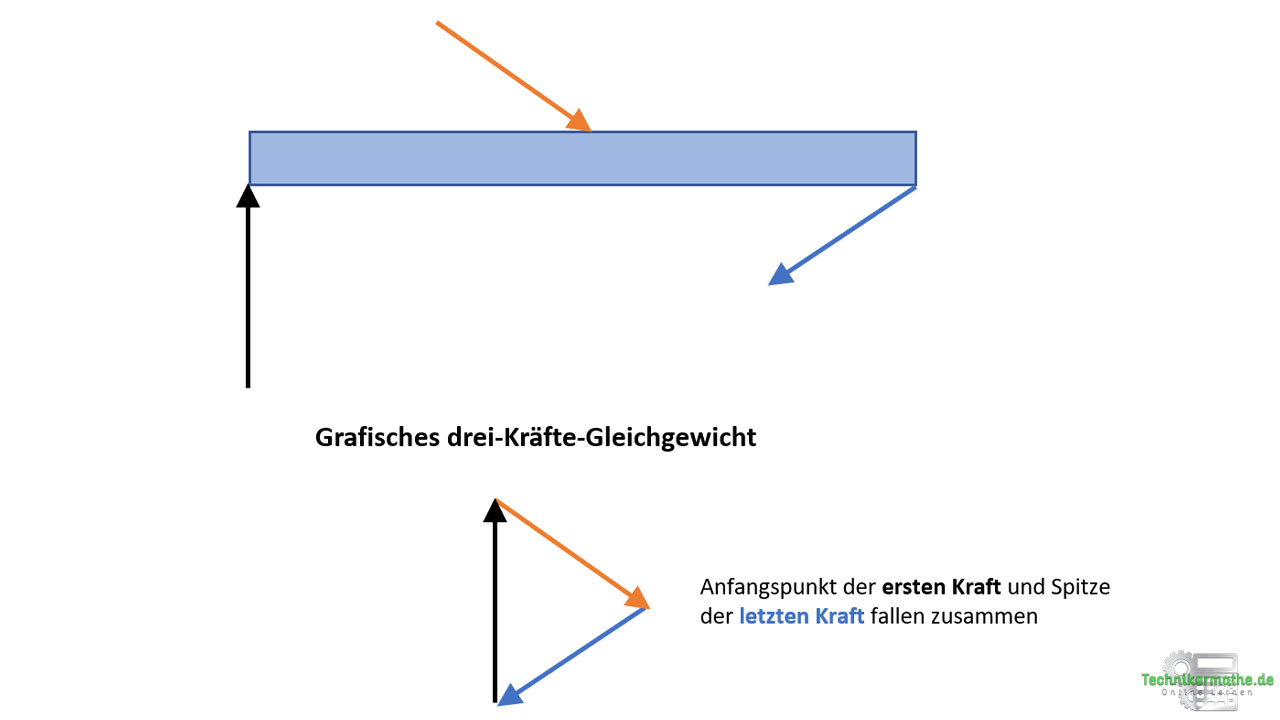
In der obigen Grafik greifen drei Kräfte an einen gewichtslosen Balken an. Wenn wir – einem Maßstab entsprechend – die grafische Vektoraddition dieser Kräfte durchführen, dann ergibt sich ein geschlossenes Kräftedreieck. Wir haben zuerst die schwarze Kraft verwendet, dann haben wir die orangene Kraft an die Spitze der schwarzen Kraft gelegt und dann die blaue Kraft an die Spitze der orangenen Kraft. Der Anfangspunkt der ersten Kraft berührt die Spitze der letzten Kraft.
Alle drei Kräfte befinden sich damit im Gleichgewicht und damit auch der obige Balken (wenn wir von einem gewichtslosen Balken ausgehen). Wird natürlich ein Balken betrachtet, bei welchem das Gewicht berücksichtigt werden muss – was in der Realität der Fall ist – dann muss zusätzlich die vertikal nach unten gerichtete Gewichtskraft berücksichtigt werden. Dann ändert sich natürlich das obige Krafteck und es muss eine zusätzliche 4. Kraft berücksichtigt werden.
Wir wollen uns nun anschauen, wie du ein grafisches Kräftegleichgewicht bei zwei bzw. drei gegebenen Kräften anwenden kannst, um unbekannte Kräfte zu bestimmen.
Beispiel 1 : Zwei-Kräfte-Gleichgewicht
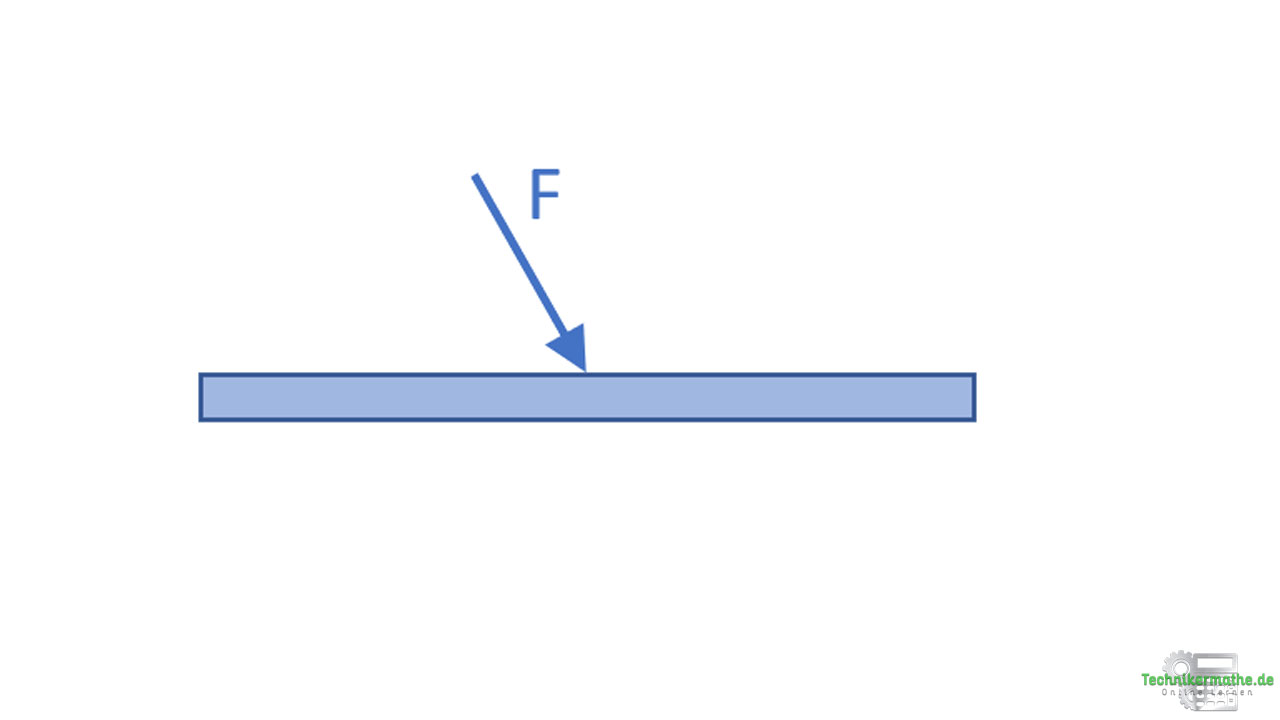
Gegeben sei der obige Balken auf welchen eine Kraft F= 12 kN wirkt.
Füge eine Kraft so ein, dass sich der obige Balken im Gleichgewicht befindet!
Damit sich der Balken im Gleichgewicht befindet, müssen wir eine Kraft so einfügen, dass
- sie die gleiche Größe wie die Kraft F aufweist,
- sie auf derselben Wirkungslinie liegt und
- sie genau entgegengesetzt gerichtet ist.
Damit müssen wir die Kraft wie folgt einzeichnen:
Die Größe der Kraft muss der Größe der gegebenen Kraft entsprechen, also 12 N. Die einzufügende Kraft muss auf derselben Wirkungslinie wie die Kraft F liegen und genau entgegengesetzt gerichtet sein. Die beiden Kräfte kompensieren sich. Die Summe der auf den Balken wirkenden Kräfte ist also Null. Demnach befindet sich der Balken im Gleichgewicht.
Beispiel 2 : Lagerkräfte bestimmen – Drei Kräftegleichgewicht
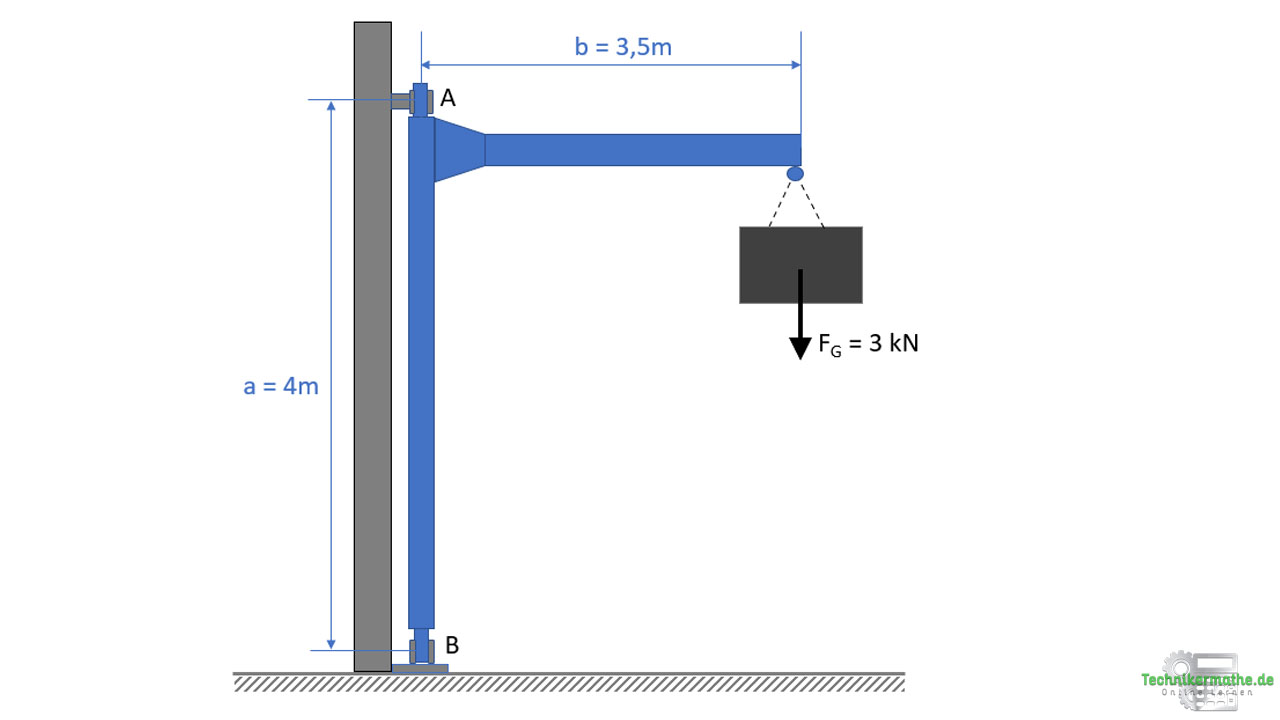
Gegeben sei der obige Wanddrehkran, welcher im Lager B durch ein zweiwertiges Stützlager und im Lager A durch ein einwertiges Halslager gehalten wird.
Bestimme die Lagerkräfte in A und B zeichnerisch!
Wir stellen uns zunächst die Frage, welche Kräfte an dem Kran wirken?
Lagerkräfte
Ein einwertiges Lager (auch Loslager) überträgt nur Kräfte senkrecht zur Stützebene. Im obigen Fall überträgt das Halslager A eine horizontale Kraft. Wir kennen also die Wirkungslinien dieser Kraft, nicht aber die Richtung oder aber die Größe dieser Kraft.
Lagerkraft A:
Bekannt: Wirkungslinie
Unbekannt: Richtung, Größe
Ein zweiwertiges Lager (auch Festlager) überträgt eine vertikale und eine horizontale Lagerkraft, die auch zu einer resultierenden Lagerkraft zusammengefasst werden kann. Wir kennen die Richtung, die Wirkungslinie und die Größe dieser resultierenden Lagerkraft nicht. Wir wissen nur, dass die Wirkungslinie der Kraft durch das Lager B geht.
Lagerkraft B:
Unbekannt: Wirkungslinie, Richtung, Größe
Äußere Kräfte
Es wirkt die Gewichtskraft der Last mit FG = 3 kN. Wir kennen die Wirkungslinien der Kraft, die Größe sowie die Richtung (vertikal nach unten).
Gewichtskraft FG
Bekannt: Wirkungslinie, Größe, Richtung
Maßstab und Freischnitt
Es wirken demnach die drei Kräfte A, B und FG am Wanddrehkran. Der wichtigste Teil der Lösung besteht nun in der Konstruktion der noch unbekannten Wirkungslinie der Lagerkraft B.
Wir betrachten nun zunächst den Freischnitt, d.h. wir reduzieren den Wanddrehkran auf seine Abmessungen und tragen die drei Kräfte ein. Lager A und B weisen einen Abstand von 4m zueinander auf, Lager A und Kraft FG einen Abstand von 3,5 m. Hier müssen wir für die Abmessungen einen geeigneten Maßstab wählen (m können wir nicht einzeichnen). Wir wählen beliebig:
Maßstab Abmessungen:
4m = 8 cm
3,5 m = 7 cm
Für die Kraft FG = 3 kN müssen wir ebenfalls einen Maßstab wählen, so dass wir diese ihrer Größe entsprechend einzeichnen können. Hier wählen wir beliebig:
Maßstab Kraft:
3 kN = 6cm
Der Freischnitt ergibt sich dann wie folgt:
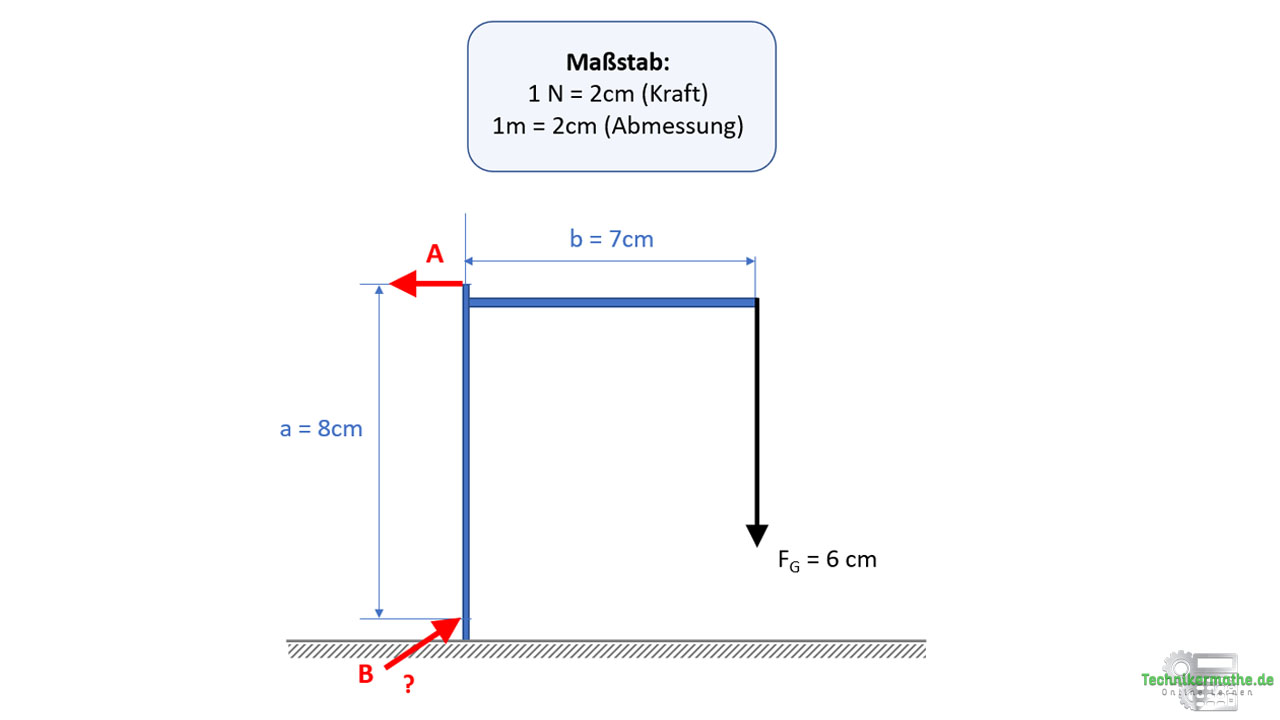
Die Wirkungslinie der Lagerkraft A ist bekannt, hier suchen wir die Größe und Richtung (die wir als nach links wirkend angenommen haben). Die Lagerkraft B ist einfach beliebig eingezeichnet worden, hier kennen wir aber weder Wirkungslinie, noch Größe oder Richtung. Wie können wir nun zunächst die Wirkungslinie der Lagerkraft B bestimmen?
Verschieben wir die Kraft A und die Gewichtskraft FG auf ihren bekannten Wirkungslinien so lange, bis diese sich schneiden, dann haben wir den Schnittpunkt S gegeben:
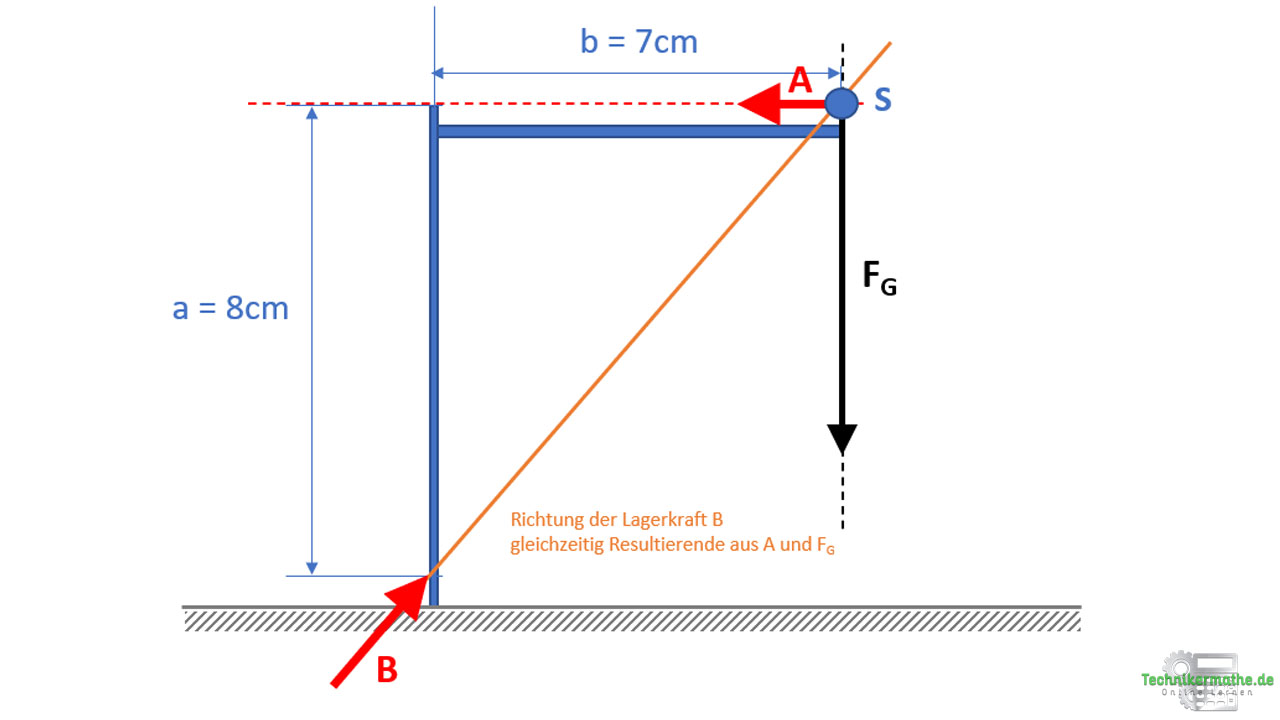
Würden wir die beiden Kräfte A und FG zu einer Resultierenden zusammenfassen, dann hätten wir nur noch diese resultierende Kraft gegeben und die Lagerkraft B. Bei zwei Kräften im Kräftegleichgewicht gilt, dass diese auf derselben Wirkungslinien liegen müssen. Wir wissen, dass die Lagerkraft B durch das Lager B verläuft und wir wissen, dass die Resultierende aus A und FG durch den Schnittpunkt S verläuft. Wir können also einfach diese beiden Punkte miteinander verbinden und erhalten damit die Wirkungslinie der Resultierenden und der Lagerkraft B.
Damit haben wir also die Wirkungslinien der Lagerkraft B bereits gegeben. Unbekannt ist weiterhin die Größe und die Richtung.
Wir können nun das drei-Kräfte-Gleichgewicht mittels grafischer Vektoraddition bestimmen. Da wir die Richtungen der Kräfte A und B nicht kennen, sondern nur die Wirkungslinien, müssen wir diese so anlegen, dass die Kräfte ein geschlossenen Krafteck ergeben.
Wir beginnen mit der bekannten Kraft FG und zeichnen diese mit 6cm ein, danach legen wir die Wirkungslinie der Kraft B an und danach die Wirkungslinien der Kraft A an die Wirkungslinie der Kraft B:
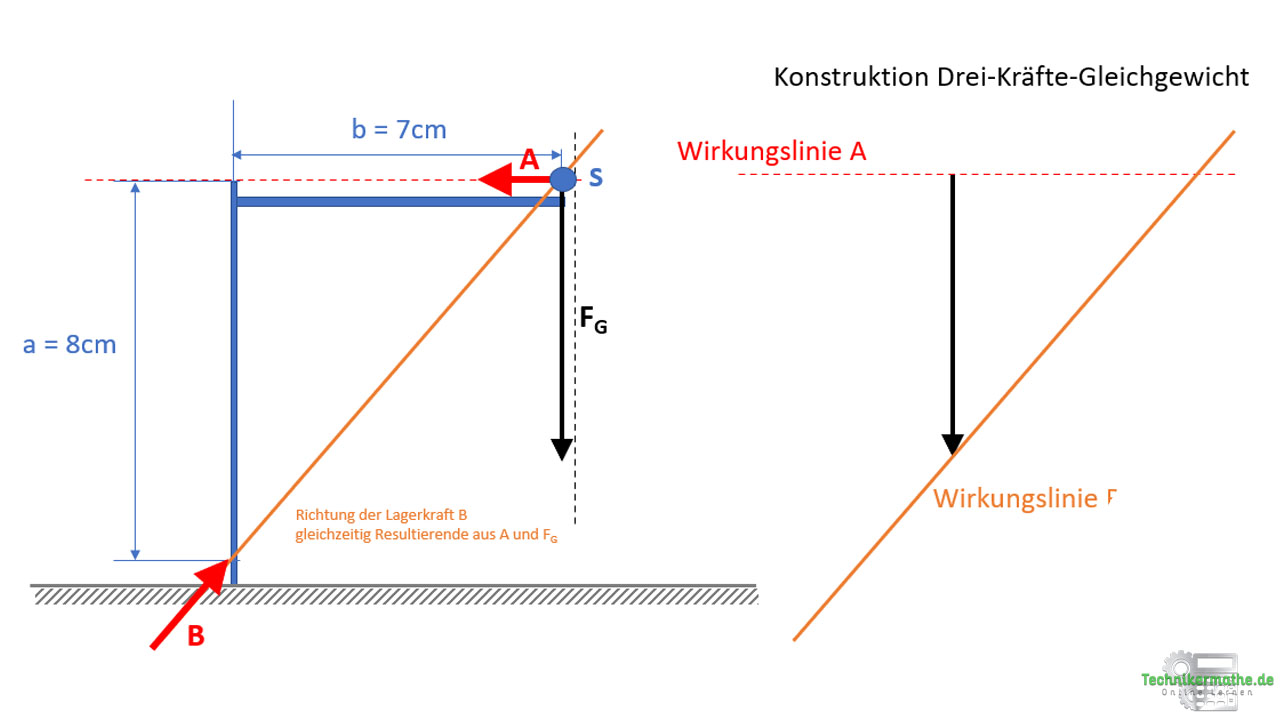
Da bei einem Kräftegleichgewicht die vorherigen Kräfte immer mit der Spitze am Anfangspunkt der nachfolgenden Kräfte liegen, müssen die Kräfte wie folgt wirken:
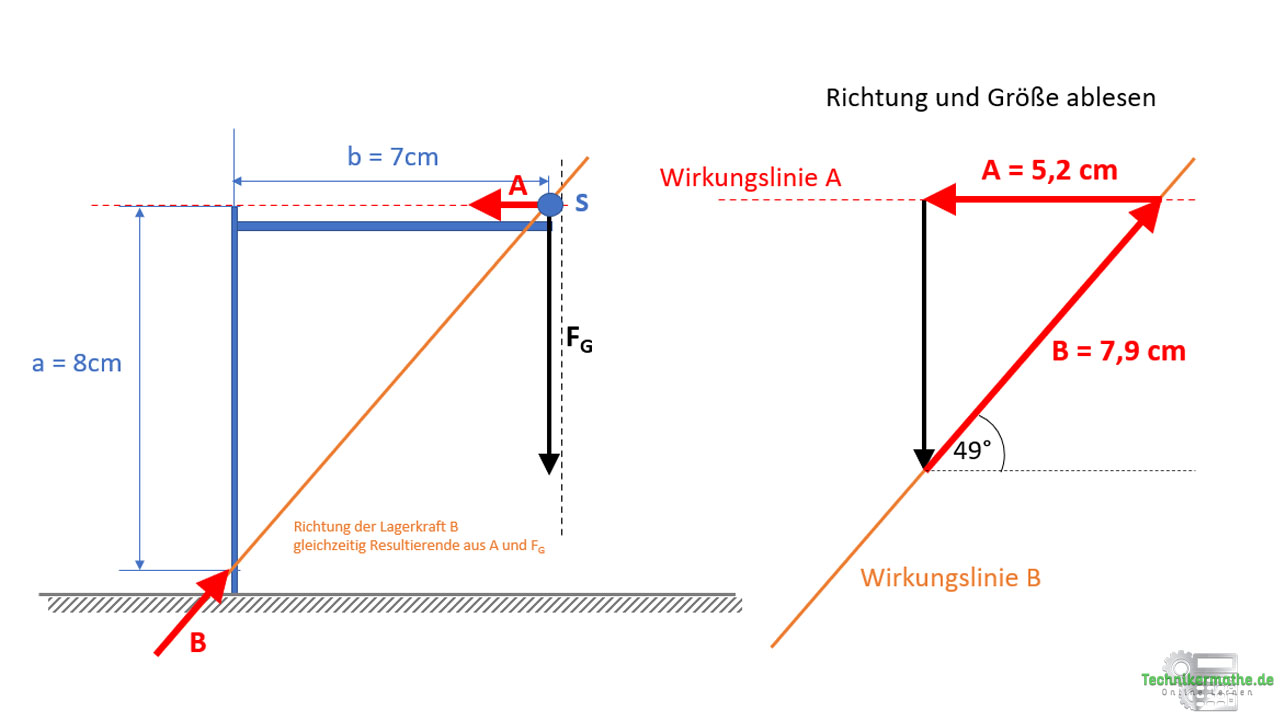
Mittels Geodreieck kannst du nun die Größe ablesen (Länge der Kraftpfeile A und B) sowie die Richtung von B (Winkel zur Horizontalen). Es ergibt sich dann ungefähr:
Zusammenfassung der Vorgehensweise zur Bestimmung der unbekannte Lagerkräfte bei drei Kräften (Grafisches Kräftegleichgewicht):
- Zunächst überlegst du dir welche Kräfte auf den Körper wirken und welche Informationen du bezüglich Wirkungslinie, Größe und Richtung gegeben hast.
- Dann zeichnest du den Freischnitt und berücksichtigst die Abmessungen und die Größe, indem du einen Maßstab festlegst.
- Danach überlegst du dir, welche zwei Kräfte du in einen gemeinsamen Punkt verschieben kannst (Schnittpunkt 1). Das können nur Kräfte sein, deren Wirkungslinien bekannt sind.
- Von diesem Schnittpunkt ausgehend ziehst du eine Verbindung zu dem Schnittpunkt durch das Lager, für welches die Wirkungslinien unbekannt ist. Du hast dann die Wirkungslinien dieser Lagerkraft bestimmt.
- Danach konstruierst du ein grafisches drei-Kräfte-Gleichgewicht, unter Berücksichtigung der Wirkungslinien der unbekannten Lagerkräfte.
- Zum Schluss zeichnest du die Kräfte ein und liest mittels Geodreieck die Längen sowie die Richtungen der unbekannten Lagerkräfte ab.
Nachdem du jetzt alles zum Thema Grafisches Kräftegleichgewicht kennst, zeigen wir dir in der folgenden Lerneinheit ein weiteres Beispiel zur Anwendung des drei-Kräfte-Gleichgewichts auf.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






