TM1 – Beispiele: Lagerkräfte, Seilkräfte und Stabkräfte berechnen

Wir betrachten die Berechnung von unbekannten Kräften aus den drei Gleichgewichtsbedingungen. Dazu schauen wir uns zwei Aufgaben an und zeigen, wie du die unbekannten Kräfte (Lagerkräfte, Seilkräfte und Stabkräfte) freischneidest und dann aus den Gleichgewichtsbedingungen berechnest. Zusätzlich können noch weitere Schritte wie die Berechnung des Winkels mittels Trigonometrie sowie die Kräftezerlegung notwendig sein.

Wir wollen uns in dieser Lerneinheit mal einige Beispiele zum allgemeinen Kräftesystem anschauen. Dabei betrachten wir komplexere Beispielen in denen wir Stabkräfte, Seilkräfte und Lagerkräfte bestimmen.

Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.

Aufgabe 1: Seilkraft und Lagerkräfte bestimmen

Aufgabenstellung

Seilkraft bestimmen, Seilkraft, Lagerkräfte, Gleichgewichtsbedingungen, Beispiel Seilkraft — Lagerkräfte bestimmen und Seilkraft ermitteln

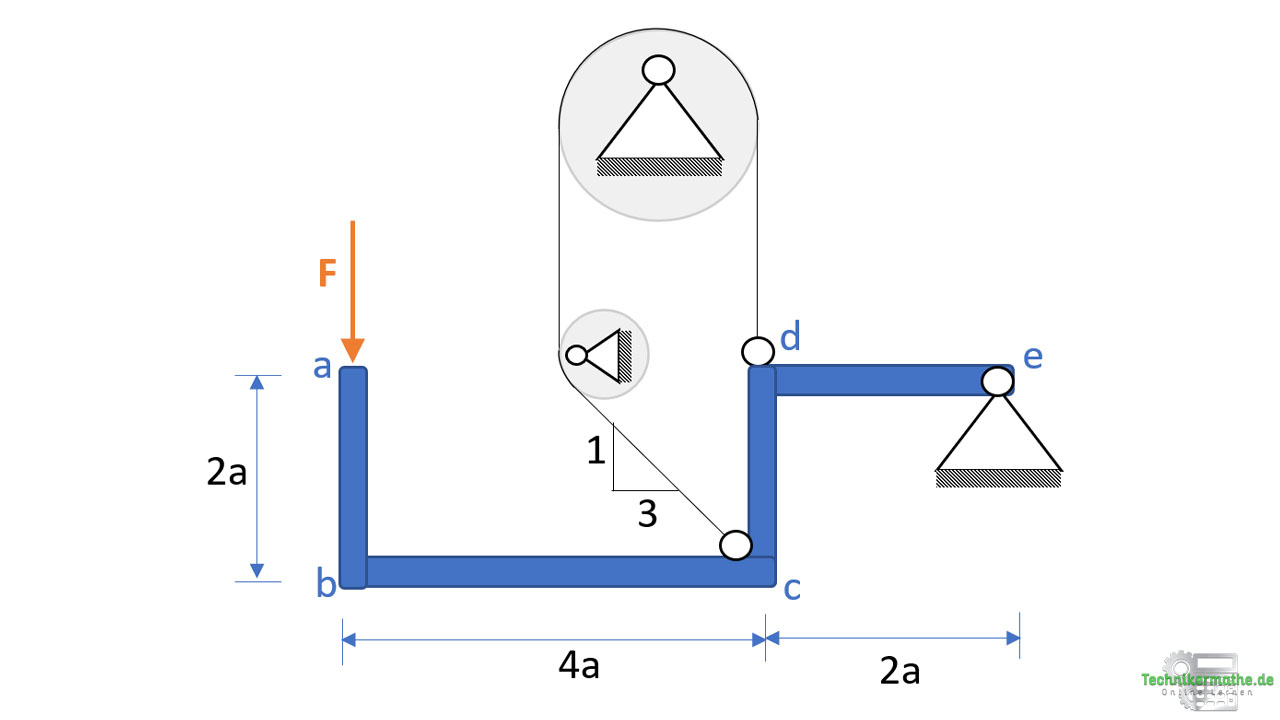
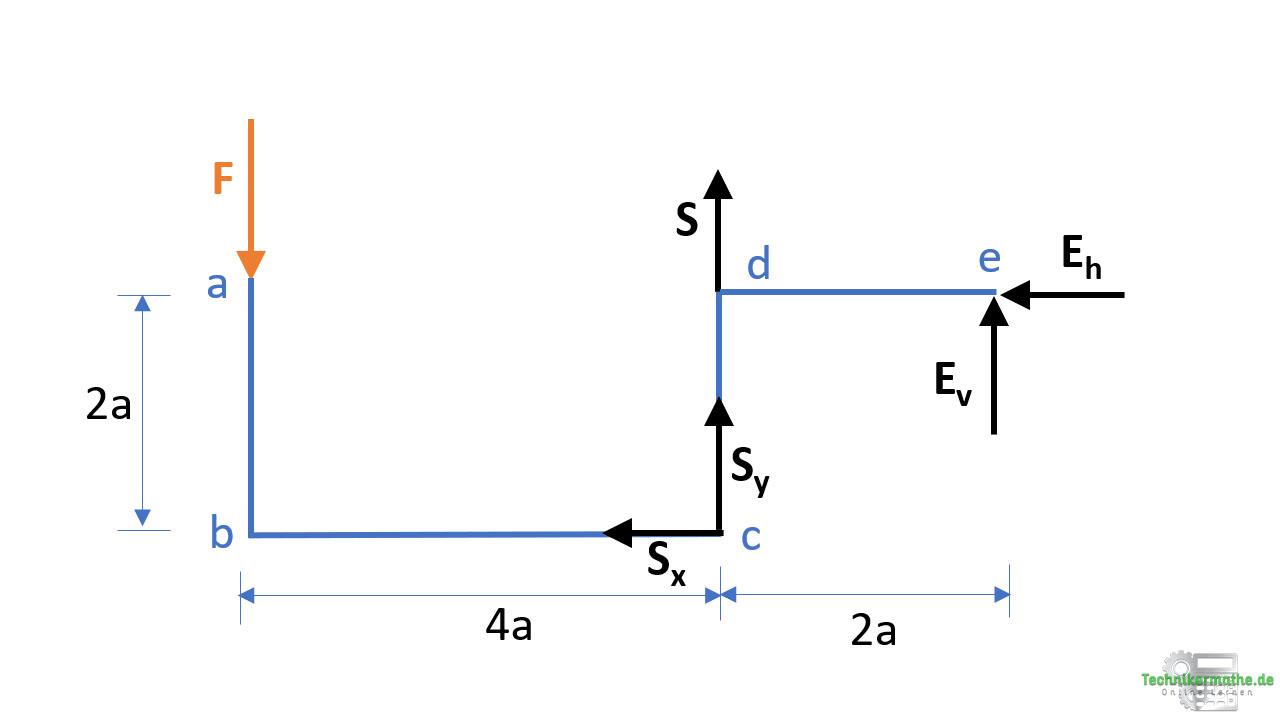
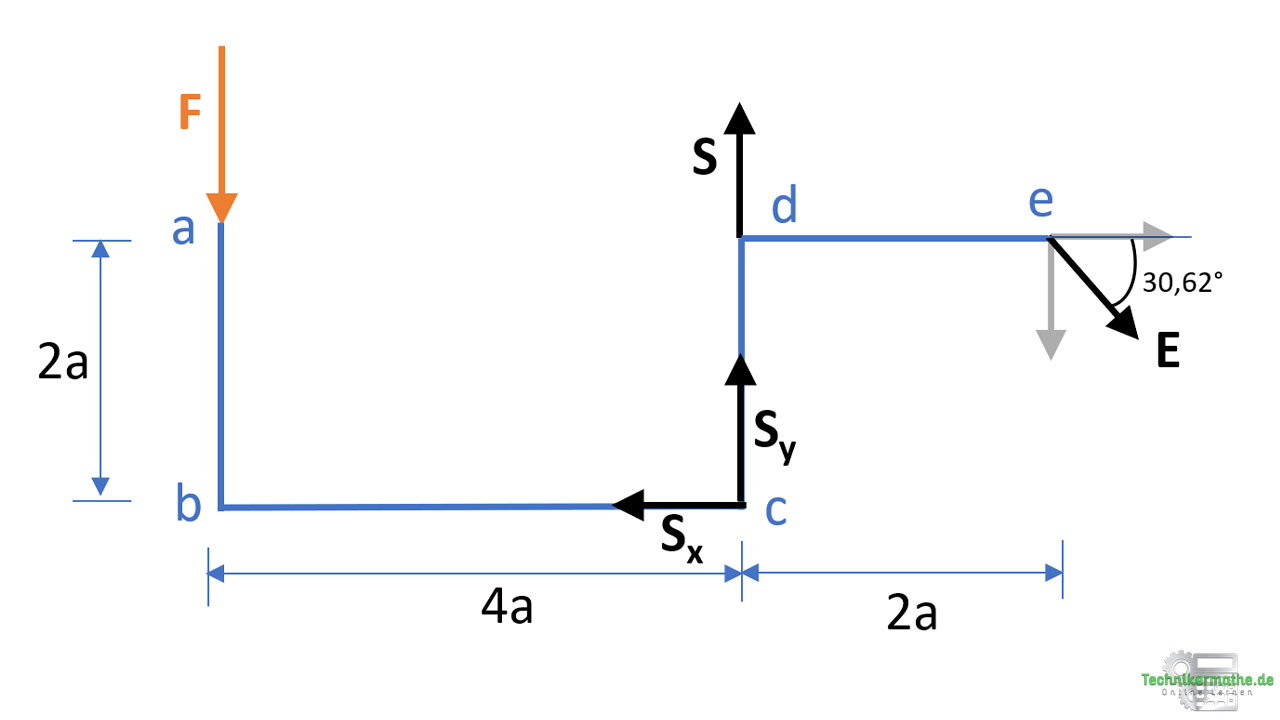
Gegeben sei der obige Balkenzug. Der Balkenzug ist bei e drehbar gelagert (Festlager) und wird durch ein Seil bei c und d gehalten. Die Reibung zwischen Seil und Rollen soll vernachlässigt werden.

Gegebene Größen:

$F = 10 kN$

$a = 1m$

Wie groß ist die Seilkraft in c bzw. d und die Auflagerkräfte in e?

Schritt 1: Freischnitt aller gesuchten Kräfte

Der Freischnitt muss immer so erfolgen, dass die zu bestimmende Kraft (hier: Seilkraft) freigeschnitten wird. In diesem Fall muss also ein Schnitt durch das Seil gemacht werden, damit die Seilkraft abgetragen werden kann. Zusätzlich dazu lösen wir das System auch von den Auflagern (hier e) und tragen die Lagerkräfte E_v und E_h ab.

Merk’s dir!

Ein Seil überträgt nur Zugkräfte entlang der Seilachse. Beim Freischnitt muss also an dem Rahmen für das Seil eine Zugkraft angebracht werden.

Lagerkräfte bestimmen, Seilkraft bestimmen, Freischnitt, Lagerkräfte, Seilkraft, Berechnung — Freischnitt: Seilkraft und Lagerkräfte

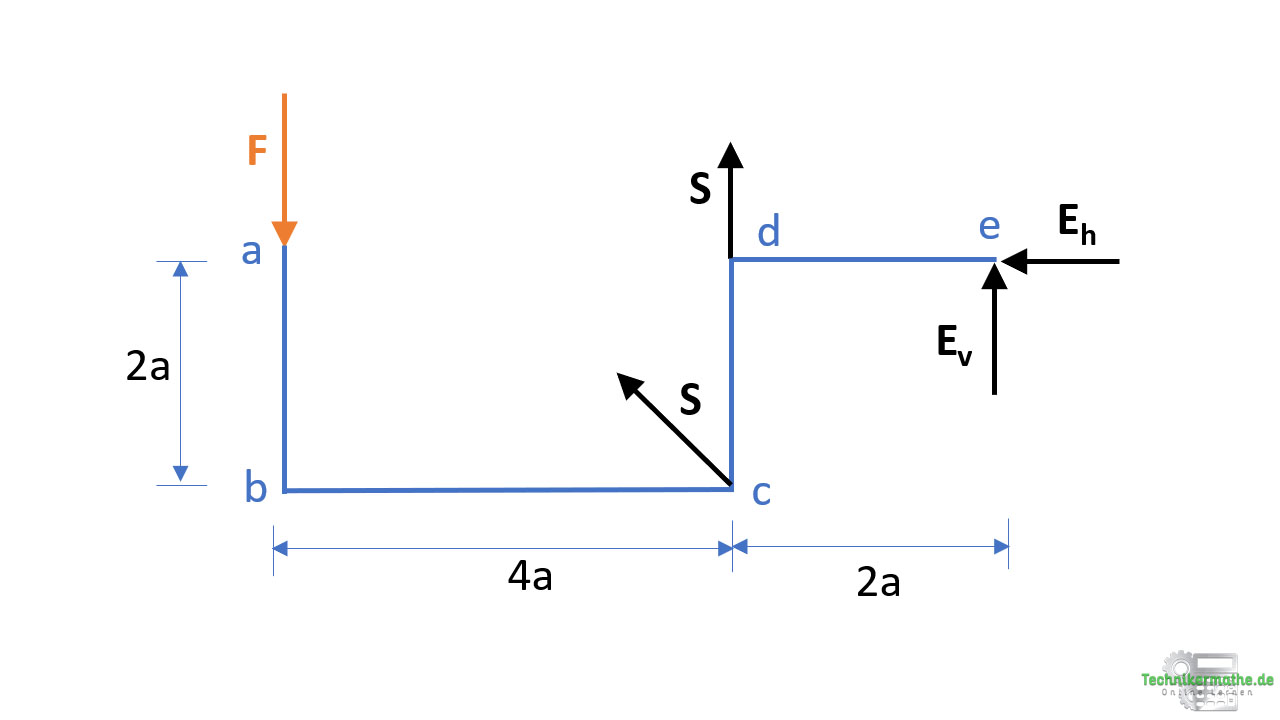
Wir müssen beim Abtragen der Kräfte berücksichtigen, dass die Seilkräfte an beiden Seiten gleich groß sind und bezeichnen die Seilkraft mit S.

Damit wir aus den Gleichgewichtsbedingungen die unbekannte Seilkraft S sowie die unbekannten Lagerkräfte E_h und E_v bestimmen können, müssen wir alle Kräfte die nicht in x- oder y-Richtung wirken in ihre Komponenten zerlegen.

Schritt 2: Kräftezerlegung

In dem obigen Beispiel muss die Seilkraft S im Punkt c in ihre x– und y-Komponente zerlegt werden. Wir kennen den Winkel der Seilkraft zur Horizontalen bzw. Vertikalen nicht, es ist aber die Steigung dieser in der Aufgabenstellung angegeben. Aus der Steigung kann mittels Trigonometrie am rechtwinkligen Dreieck der Winkel berechnet werden:

Lagerkräfte bestimmen, Steigung bestimmen, Steigung, Winkel, Seilkraft, Trigonometrie — Bestimmung des Winkels der Seilkraft mittels Trigonometrie

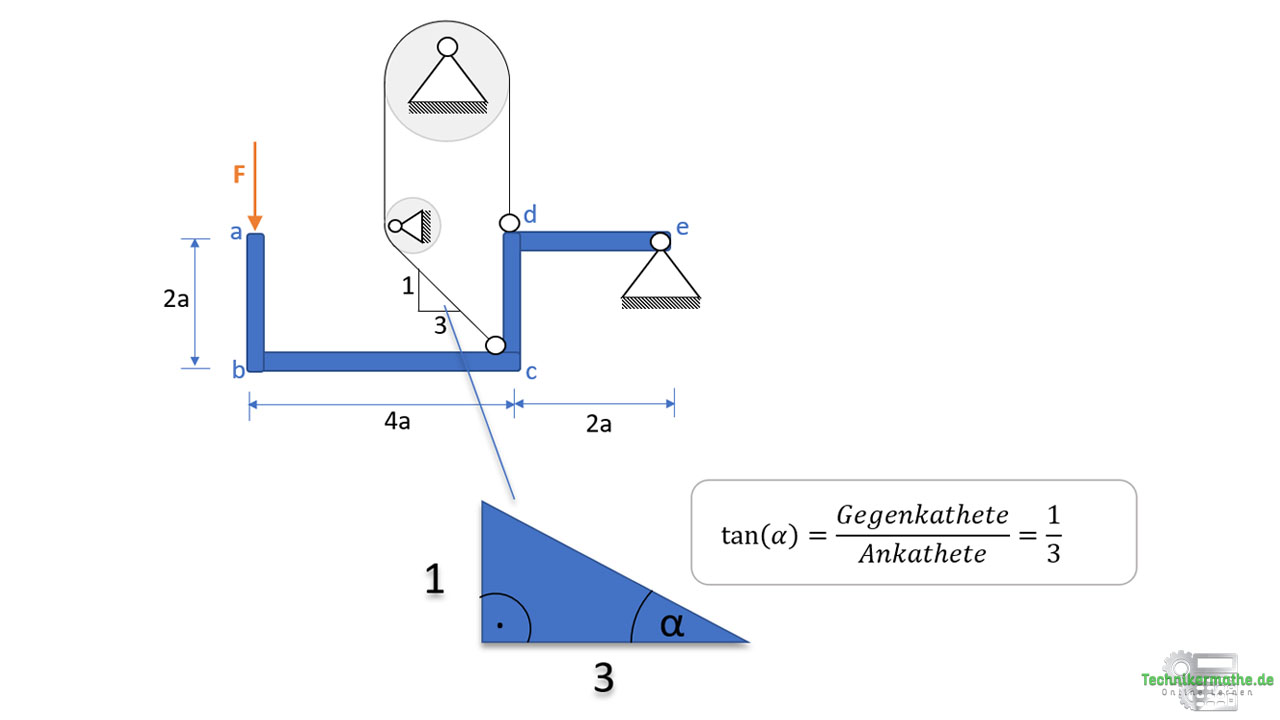
Mittels Tangens können wir den Winkel α zur Horizontalen bestimmen. Auflösen nach α ergibt:

$\tan(\alpha) = \dfrac{1}{3}$ | $tan^{-1}$

$\alpha = \tan^{-1}(\dfrac{1}{3})$

$\alpha = 18,43^{\circ}$

Als nächstes kann die Seilkraft im Punkt c in ihre x– und y-Komponente zerlegt werden:

$S_x = S \cdot \cos(\alpha) = S \cdot \cos(18,43^{\circ}) = S \cdot 0,949$

$S_y = S \cdot \sin(\alpha) = S \cdot \sin(18,43^{\circ}) = S \cdot 0,316$

Lagerkräfte bestimmen, Seilkraft bestimmen, Kräftezerlegung, Seilkraft, Lagerkräfte — Komponenten der Seilkraft einfügen

Schritt 3: Gleichgewichtsbedingungen

Wir wollen nun die Seilkraft und die unbekannten Lagerkräfte bestimmen. Dazu wenden wir die drei Gleichgewichtsbedingungen in der Ebene an:

Horizontale Gleichgewichtsbedingung:

$\sum F_{ix} = 0: \; \; \; -E_h - S_x = 0$

$-E_h - S \cdot 0,949 =0$

Vertikale Gleichgewichtsbedingung:

$\sum F_{iy} = 0 \; \; \; E_v + S_y + S - F = 0$

$E_v + S \cdot 0,316 + S - F = 0$

Aus den obigen Gleichgewichtsbedingungen kann keine der Unbekannten bestimmt werden.

Wir benötigen noch die Momentengleichgewichtsbedingung.

Um aus der Momentengleichgewichtsbedingung eine unbekannte Kraft bestimmen zu können, muss der Bezugspunkt sinnvoll gewählt werden. Legen wir den Bezugspunkt in das Lager E, so fallen bei der Momentenberechnung die Lagerkräfte E_hund E_vaus der Berechnung heraus:

$\sum M^E = 0 \; \; \; F \cdot 6a - S_x \cdot2 a - S_y \cdot 2a - S \cdot 2a = 0$

$F \cdot 6a - S \cdot 0,949 \cdot2 a - S \cdot 0,316 \cdot 2a - S \cdot 2a = 0$

Wir haben alle rechtsdrehenden Momente negativ berücksichtigt und alle linksdrehenden Momente (hier: F⋅6a) positiv. Wir können nun die Gleichung nach S auflösen. Da jedes Glied von a abhängig ist, können wir zunächst durch a teilen:

$F \cdot 6 - S \cdot 0,949 \cdot 2 - S \cdot 0,316 \cdot 2 - S \cdot 2 = 0$ |Faktoren zusammenfassen

$6F - 1,898 S - 0,632 S - 2 S = 0$ |aller Glieder mit S zusammenfassen

$6F - 4,53 S = 0$ | $+4,53 S$

$6F = 4,53 S$ | $:4,53$

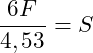$\dfrac{6F}{4,53} = S$ | $F = 10 kN$ einsetzen

$\dfrac{6 \cdot 10 kN}{4,53} = S$

$S = 13,25 kN$

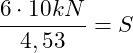
Aus der vertikalen und horizontalen Gleichgewichtsbedingung können wir nun die Lagerkräfte bestimmen.

Horizontale Gleichgewichtsbedingung:

$-E_h - S \cdot 0,949 =0$

$E_h = - S \cdot 0,949 = -13,25 kN \cdot 0,949$

$E_h = -12,57 kN$

Das Ergebnis ist negativ, damit wirkt die Auflagerkraft E_h nach rechts und nicht – wie angenommen – nach links.

Vertikale Gleichgewichtsbedingung:

$E_v + S \cdot 0,316 + S - F = 0$

$E_v = -S \cdot 0,316 - S + F$

$E_v = - 13,25 kN \cdot 0,316 - 13,25 kN + 10 kN$

$E_v = -7,44 kN$

Das Ergebnis ist negativ, damit wirkt die Auflagerkraft E_v nach unten und nicht – wie angenommen – nach oben.

Wir können die Auflagerkräfte E_v und E_h noch zu einer resultierenden Auflagerkraft zusammenfassen. Da beide Kräfte rechtwinklig zueinander stehen, können wir hier den Satz des Pythagoras anwenden:

$E = \sqrt{E_h^2 + E_v^2} = \sqrt{(-12,57 kN)^2 + (-7,44 kN)^2} = 14,61 kN$

Der Winkel von der Horizontalen zur resultierenden Auflagerkraft wird mittels Tangens berechnet:

$\tan(\alpha_E) = \dfrac{E_v}{E_h}$

$\alpha_E = \tan^{-1}(\dfrac{E_v}{E_h})$

$\alpha_E = \tan^{-1}(\dfrac{-7,44 kN}{-12,57 kN})$

$\alpha_E = 30,62^{\circ}$

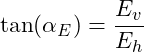
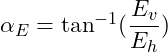
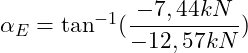
Hierbei handelt es sich um den Winkel von der Lagerkraft E_h zur Resultierenden E, also von der Horizontalen zur Resultierenden.

Seilkraft bestimmen, Lagerkräfte berechnen, resultierende Lagerkraft — Einzeichnung der resultierenden Lagerkraft

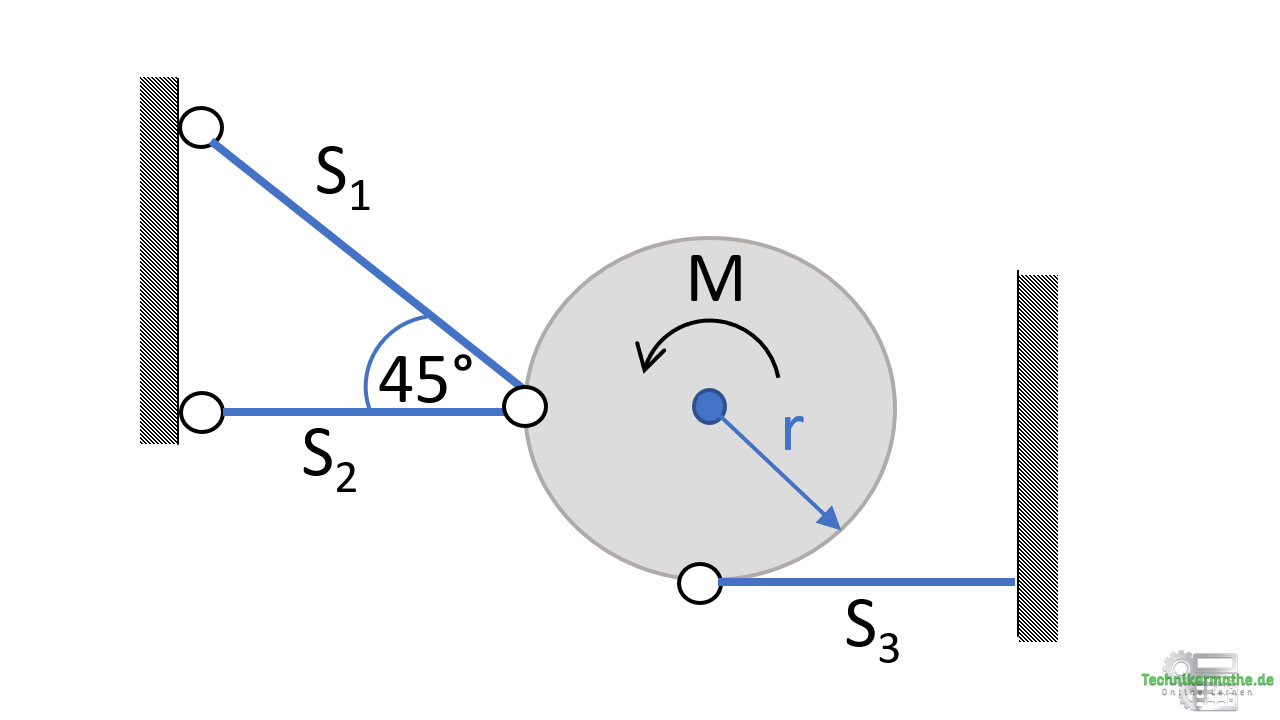
Aufgabe 2: Stabkräfte berechnen

Aufgabenstellung

Stabkraft bestimmen, Stabkraft, Lagerkräfte berechnen, Stäbe, Rolle — Lagerkräfte und Stabkraft bestimmen

Gegeben sei die obige Kreisscheibe, die von drei Stäben gehalten wird. Die Kreisscheibe wird durch ein äußeres Moment M belastet.

Gegebene Größen:

$m=15 kg$

$r=10cm$

$M=25Nm$

a) Bestimme die Stabkräfte!

b) Wie groß wird das Moment M, wenn die Stabkraft S3 Null wird?

Lösung a) Berechne die Stabkräfte

Schritt 1: Freischnitt der gesuchten Kräfte

Zunächst schneiden wir die Kreisscheibe so frei, dass die gesuchten Stabkräfte frei liegen. Wir tragen die Stabkräfte alle als Zugkräfte ab (bei einem negativen Ergebnis ist es tatsächlich ein Druckstab):

Stabkräfte berechnen, Lagerkräfte bestimmen, Freischnitt Stabkraft, Zugkraft, Rolle, Beispiel — Stabkräfte freischneiden

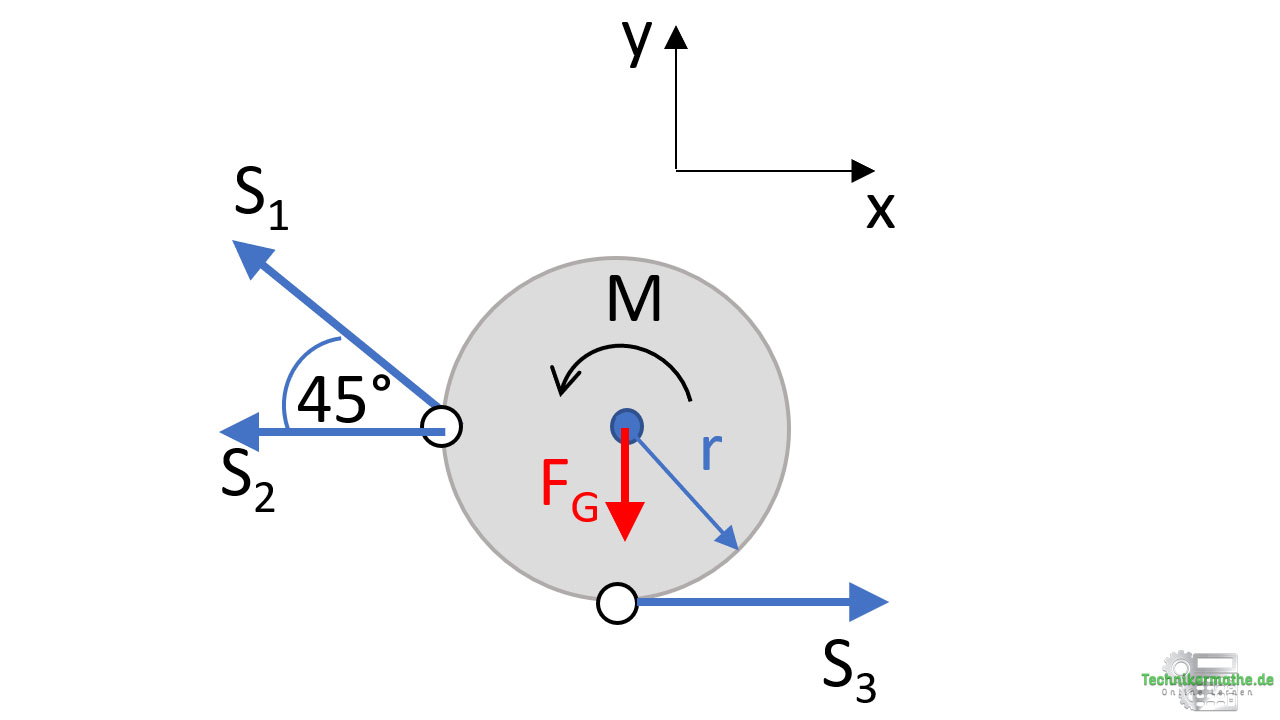
Außerdem müssen wir die Gewichtskraft der Scheibe berücksichtigen. Eine Gewichtskraft wirkt immer vertikal nach unten. Berechnet wird die Gewichtskraft durch:

$F_G = m \cdot g$

Die Gewichtskraft ist gleich Masse mal Erdbeschleunigung. Die Erdbeschleunigung bei physikalischen Berechnungen wird mit der Konstanten g = 9,81 m/s² angegeben.

Schritt 2: Kräftezerlegung

Die x-Achse und die y-Achsen werden eingeführt und zunächst alle Kräfte, die weder in x– noch in y-Richtung zeigen in ihre Komponenten zerlegt. In diesem Beispiel muss die Stabkraft S₁ in ihre Komponenten zerlegt werden:

$S_x = S_1 \cdot \cos(45^{\circ})$ negative x-Richtung

$S_y = S_1 \cdot \sin(45^{\circ})$ positive y-Richtung

Da der Winkel 45° beträgt, sind sowohl Sinus und Kosinus von 45° gleich groß:

$\sin(45^{\circ}) = \cos(45^{\circ}) = \dfrac{\sqrt{2}}{2}$

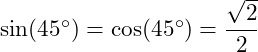
Es ergibt sich also:

$S_x = S_y =S_1 \cdot \dfrac{\sqrt{2}}{2}$

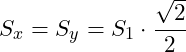
Wir tragen die beiden Komponenten an der Scheibe ab:

Stabkräfte bestimmen, Lagerkräfte, Freischnitt, Kräftezerlegung, Komponenten — Komponenten der Seilkräfte einzeichnen

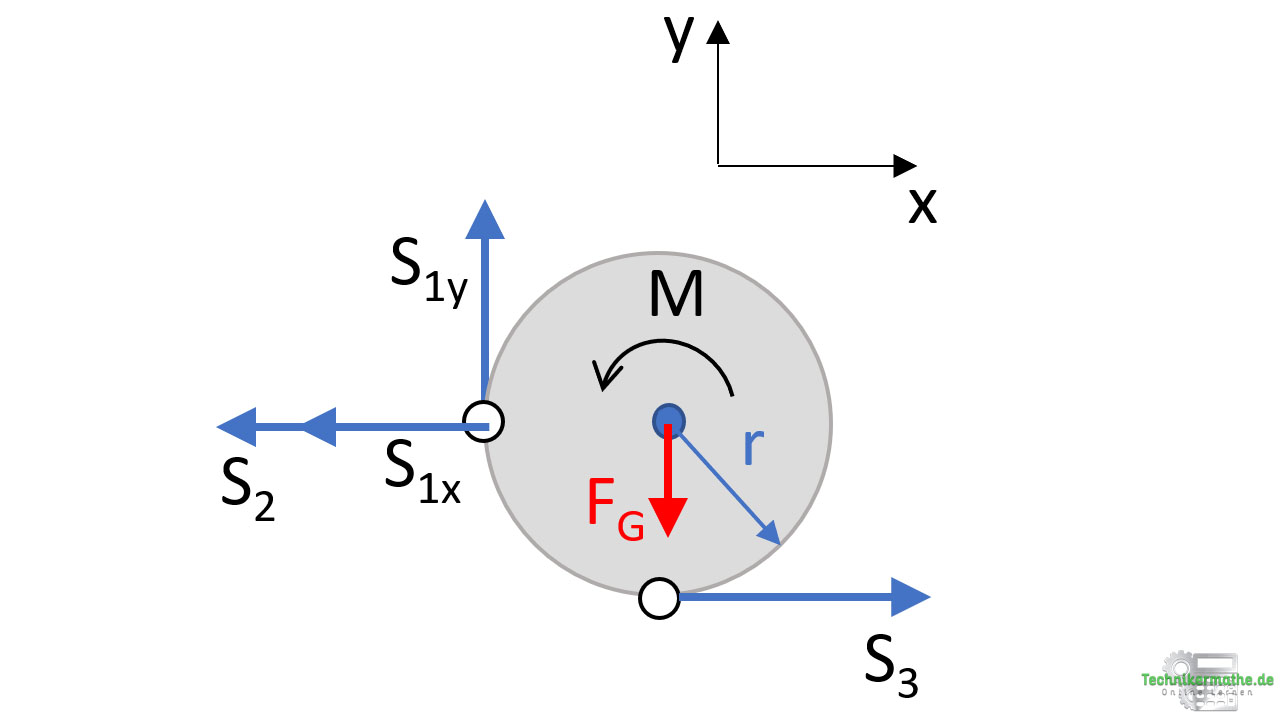
Schritt 3: Gleichgewichtsbedingungen

Als nächstes wenden wir die Gleichgewichtsbedingungen an, um die unbekannten Stabkräfte zu berechnen.

(1) $\sum F_{ix} = 0 \; \; \; -S_2 - S_{1x} + S_3 = 0$

(2) $\sum F_{iy} = 0: \; \; \; S_{1y} - F_G = 0$

Aus der vertikalen Gleichgewichtsbedingung (2) können wir die unbekannte Stabkraft S₁ berechnen:

$S_{1y} - F_G = 0$

$S_1 \cdot \dfrac{\sqrt{2}}{2} - m \cdot g = 0$

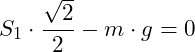
Einsetzen von m = 15 kg und g = 9,81 m/s²:

$S_1 \cdot \dfrac{\sqrt{2}}{2} - 15 kg \cdot 9,81 \frac{m}{s^2} = 0$

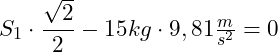
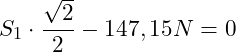$S_1 \cdot \dfrac{\sqrt{2}}{2} - 147,15 N = 0$ |+147,15 N

$S_1 \cdot \dfrac{\sqrt{2}}{2} = 147,15 N$ | $\cdot \dfrac{2}{\sqrt{2}}$

$S_1 = 147,15 N \cdot \dfrac{2}{\sqrt{2}}$

$S_1 = 208,10 N$

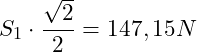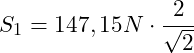
Als nächstes wenden wir die Momentengleichgewichtsbedingung an. Diese legen wir so, dass so viele Unbekannte wie möglich wegfallen. Wir haben bereits S₁ bestimmt. Wir suchen noch S₂ und S₃. Demnach können wir den Bezugspunkt so legen, dass entweder S₂ oder S₃ in der Berechnung wegfallen:

Beispiel Stabkräfte, Stabkräfte, Rolle, Scheibe, Bezugspunkt, Momentengleichgewichtsbedingung — Bezugspunkte für die Momentengleichgewichtsbedingung

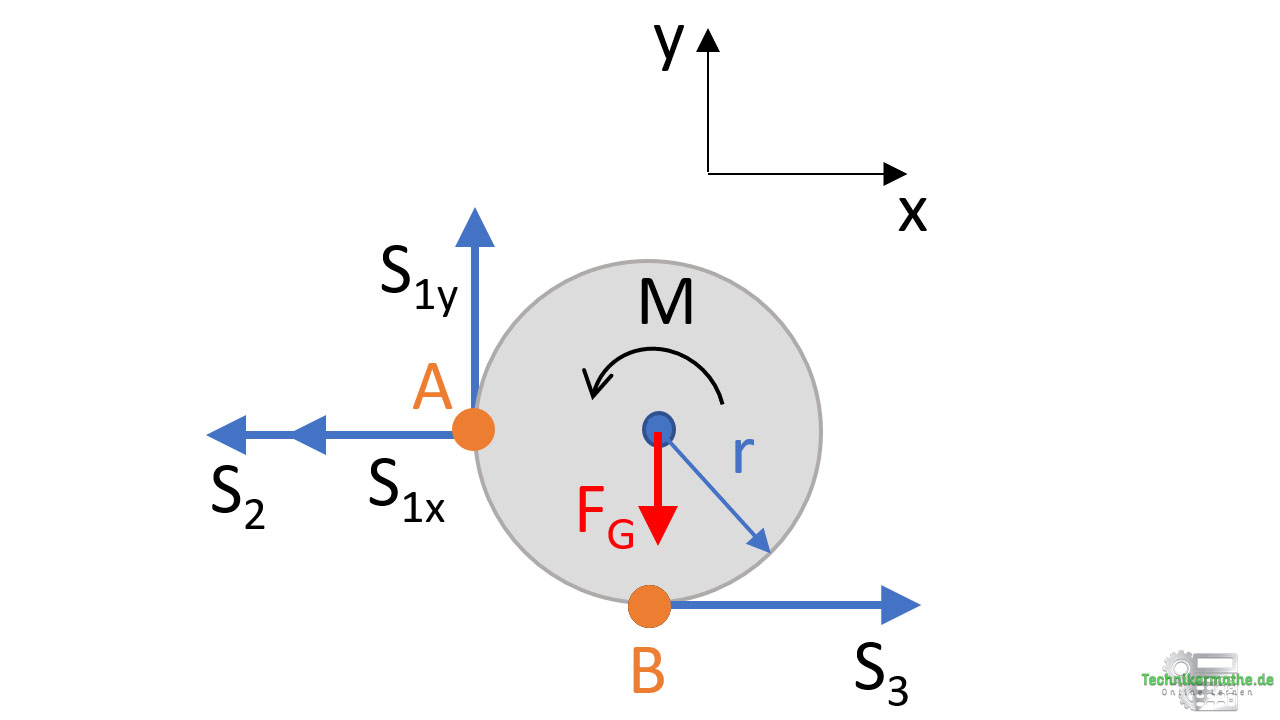
Wir wählen beliebig den Punkt A. Die Gewichtskraft weist einen Hebelarm r zum Punkt A auf und übt ein rechtsdrehendes Moment aus. Die Stabkraft S₃ weist ebenfalls den Hebelarm r auf und übt ein linksdrehendes Moment aus. Wir müssen außerdem das Moment M berücksichtigen, welches linksdrehend ist (also positiv):

$\sum M^A = 0: \; \; \; -F_G \cdot r + S_3 \cdot r + M = 0$

Wir können die Momentengleichgewichtsbedingung nach S₃ auflösen:

$-F_G \cdot r + S_3 \cdot r + M = 0$

$S_3 \cdot r = F_G \cdot r - M$

$S_3 = \dfrac{F_G \cdot r - M}{r}$

Einsetzen von r = 10 cm = 0,1m , M = 25 Nm:

$S_3 = \dfrac{147,15 N \cdot 0,1m - 25 Nm}{0,1m}$

$S_3 = -102,85 N$

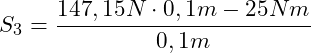
Aus der horizontalen Gleichgewichtsbedingung (1) können wir als letztes die Stabkraft S₃ bestimmen:

(1) $\sum F_{ix} = 0 \; \; \; -S_2 - S_{1x} + S_3 = 0$

$-S_2 - S_{1x} + S_3 = 0$

$S_2 = - S_{1x} + S_3$

$S_2 = -S1 \cdot \dfrac{\sqrt{2}}{2} + S_3$

$S_ 2 = -208,10 N\cdot \dfrac{\sqrt{2}}{2} + (-102,85 N) = -147,15 N - 102,85 N$

$S_ 2 = -250 N$

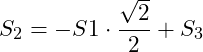
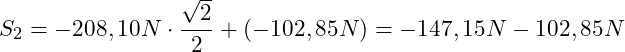
Die Stabkräfte S₂ und S₃ sind Druckkräfte, weil diese im Freikörperbild als Zugkräfte angenommen wurden und ein negatives Ergebnis resultiert ist!

Lösung b) Moment berechnen

Um herauszufinden, welchen Wert das Moment annimmt, wenn die Stabkraft S₃ Null wird, müssen wir die obige Momentengleichgewichtsbedingung aufgelöst nach S₃ gleich Null setzen:

$S_3 = \dfrac{F_G \cdot r - M}{r} = 0$

Wir können diese Gleichung deswegen heranziehen, weil hier nur die unbekannte Stabkraft S₃ enthalten ist.

$\dfrac{F_G \cdot r - M}{r} = 0$ | $\cdot r$

$F_G \cdot r - M = 0$ |+M

$F_G \cdot r = M$

$M = 147,15 Nm \cdot 0,1 m = 14,72 Nm$

Das Moment beträgt dann 14,72 Nm.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++