TM1 – Auflagerkräfte berechnen

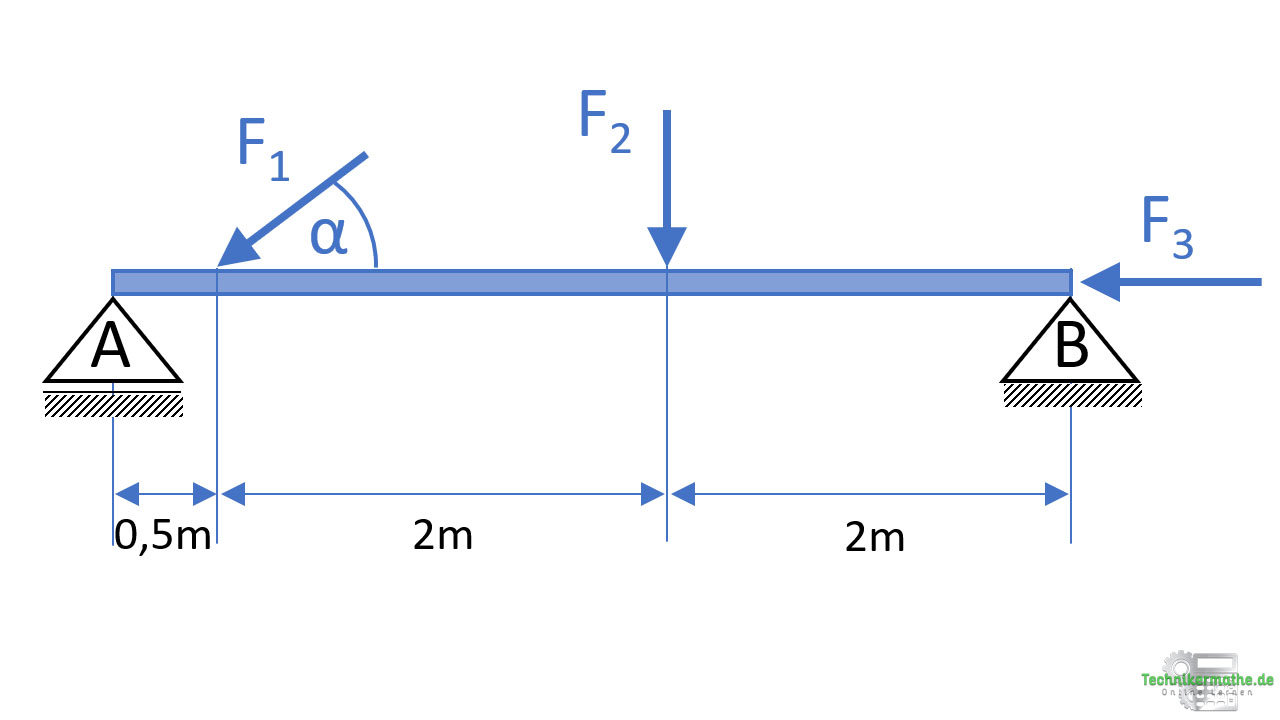
Auflagerkräfte sind die Kräfte, die an den Lagern oder Auflagerpunkten eines Bauteils wirken. Diese Kräfte entstehen als Reaktion des Bauteils auf externe Belastungen oder durch das Gewicht des Bauteils selbst. Auflagerkräfte spielen eine wichtige Rolle bei der Analyse und dem Design verschiedener Bauteile, da sie die Stabilität, das Gleichgewicht und das Gesamtverhalten unter verschiedenen Belastungsbedingungen bestimmen.

In diesem Kursabschnitt erklären wir dir einfach und anschaulich wie du die Auflagerkräfte aus den Gleichgewichtsbedingungen berechnest.

Für ein optimales Verständnis helfen dir 7 Videos und ein anschauliches Rechenbeispiel zu dem Thema “Auflagerkräfte berechnen”.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.

Auflagerkräfte – Grundlagen

Merk’s dir!

Auflagerkräfte sind die Kräfte, die von der Umwelt über eine Lagerung (ein Auflager) auf ein Bauteil oder ein Tragwerk ausgeübt werden, wenn diese Lagerung eine Verschiebung des Bauteils an der Lagerstelle verhindert.

Auflagerkräfte berechnen, Nachhilfe Techniker, Gleichgewichtsbedingungen, Auflagerkräfte — Auflagerkräfte berechnen

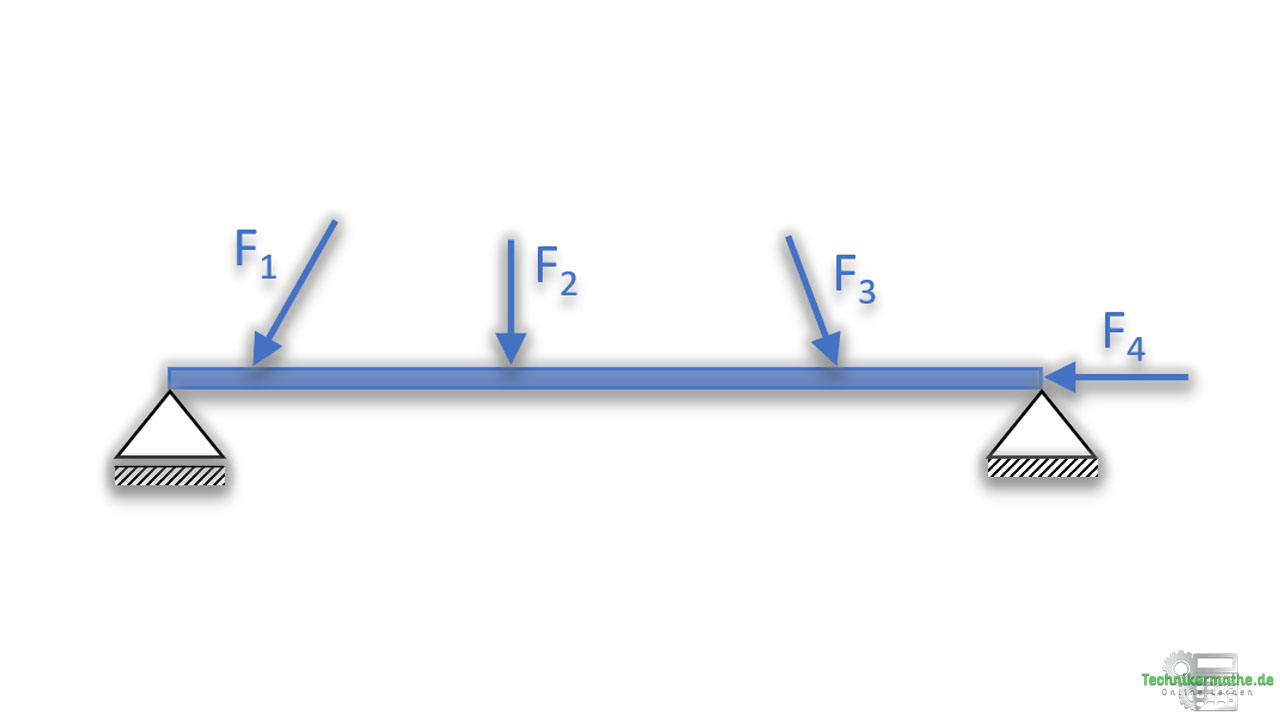
Schauen wir uns im Folgenden mal an, wie du die Auflagerkräfte aus den Gleichgewichtsbedingungen berechnen kannst.

Auflagerkräfte – Gleichgewichtsbedingungen

Auflagerkräfte können aus den Gleichgewichtsbedingungen berechnet werden. Für die Ebene gilt, dass du aus den 3 Gleichgewichtsbedingungen insgesamt 3 Auflagerkräfte berechnen kannst. In der Ebene existieren drei Gleichgewichtsbedingungen:

Gleichgewichtsbedingung in x-Richtung
Gleichgewichtsbedingung in y-Richtung
Momentengleichgewichtsbedingung

Die ersten beiden Gleichgewichtsbedingungen sagen nichts anderes aus, als dass die Summe aller Kräfte in x- und y-Richtung gleich Null (=0) sein muss, damit keine Bewegung in x- und y-Richtung stattfindet. Denn innerhalb der Statik betrachten wir ruhende Körper, weshalb keine Bewegungen auftreten dürfen.

Die Momentengleichgewichtsbedingung sagt aus, dass keine Rotation (Drehung) des betrachteten Körpers in der x,y-Ebene stattfindet. Dafür muss die Summe aller Momente auf einen beliebigen Bezugspunkt gleich Null (=0) sein. Die Summe aller Momente auf einen bestimmten Punkt darf also keine Drehwirkung des Körpers ergeben.

Schauen wir uns mal die drei Gleichgewichtsbedingungen in Formeldarstellung an.

Gleichgewichtsbedingung in x-Richtung:

$\sum F_x = 0$

Innerhalb der Gleichgewichtsbedingung in x-Richtung berücksichtigen wir nur horizontale Kräfte. Alle Kräfte die nach rechts zeigen (in positive x-Richtung) sind positiv zu berücksichtigen und alle Kräfte die nach links zeigen somit negativ.

Gleichgewichtsbedingung in y-Richtung:

$\sum F_y = 0$

Innerhalb der Gleichgewichtsbedingung in y-Richtung berücksichtigen wir nur vertikale Kräfte. Hier gilt, dass alle Kräfte die nach oben zeigen (in positive y-Richtung) positiv und somit alle Kräfte die nach unten zeigen negativ zu berücksichtigen sind.

Momentengleichgewichtsbedingung:

$\sum M = 0$

Innerhalb der Momentengleichgewichtsbedingung betrachten wir alle Momente auf einen vorher festgelegten Bezugspunkt. Dabei sind linksdrehende Momente (gegen den Uhrzeigersinn) positiv zu berücksichtigt und rechtsdrehende Momente (mit dem Uhrzeigersinn) negativ.

Videoreihe: Gleichgewichtsbedingungen

In den folgenden Videos zeige ich dir, wie du die drei Gleichgewichtsbedingungen anwendest.

Gleichgewichtsbedingungen

Auflagerkräfte berechnen – Vorgehensweise

Um die Auflagerkräfte berechnen zu können, kannst du dir die folgende Vorgehensweise merken.

Schritt 1: Freischnitt

Zunächst musst du den betrachteten Körper/das Tragwerk von seiner Umgebung freischneiden. Damit trennst du das Tragwerk von seinen Auflagern und trägst dann die Auflagerkräfte ab. Dazu solltest du wissen, welche Auflager gegeben sind und welche Kräfte die jeweiligen Auflager übertragen.

Ein Festlager überträgt zum Beispiel eine vertikale und eine horizontale Kraft.
Ein Loslager überträgt eine vertikale oder horizontale Kraft (je nachdem wie es angebracht ist).
Eine feste Einspannung überträgt eine vertikale und eine horizontale Kraft sowie ein Moment.

Auflagerkräfte berechnen, Nachhilfe Techniker, Freischnitt, Festlager, Loslager, Feste Einspannung — Übersicht der gängigen Lager und ihrer Lagerreaktionen

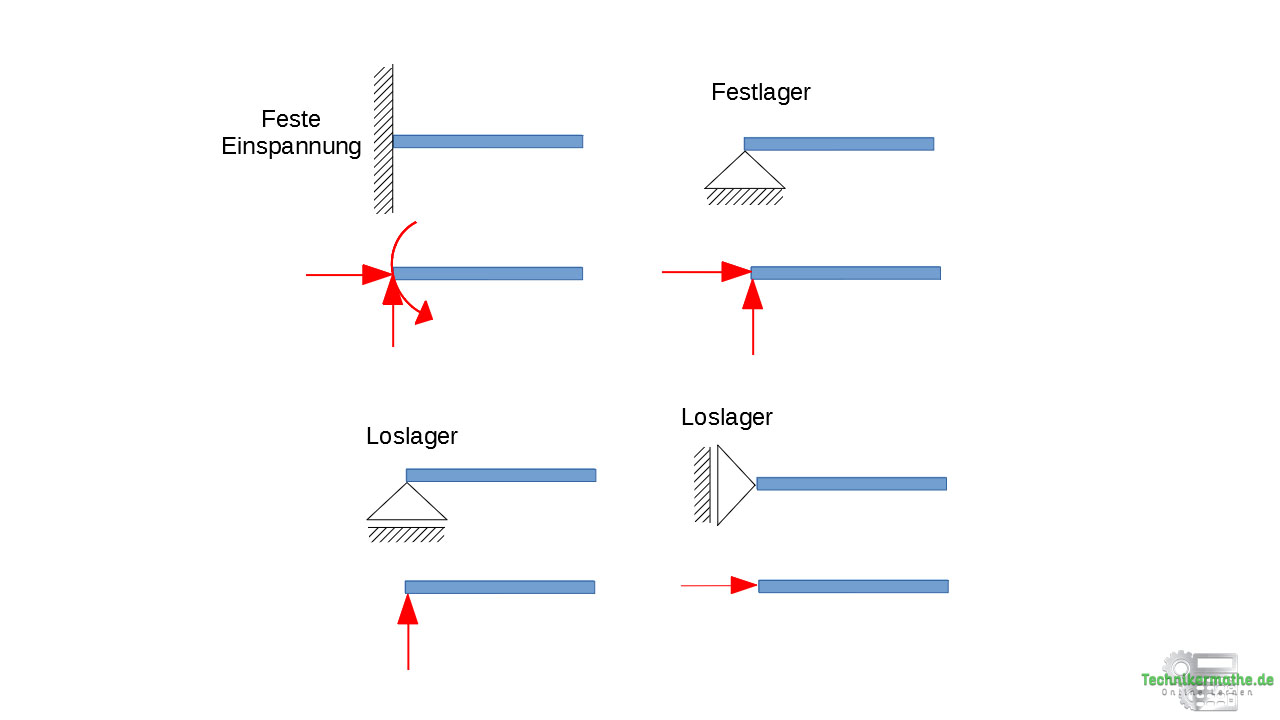
Wichtig ist nur, dass du Wirkungslinie der Auflagekräfte kennst. Wenn ein Loslager also eine vertikale Kraft überträgt, kannst du diese nach oben oder nach unten gerichtet einzeichnen. Dasselbe gilt auch für horizontale Kräfte. Wenn du also ein Festlager gegeben hast, kannst du die horizontale Kraft nach links oder rechts gerichtet einzeichnen. Auch für Momente beispielsweise bei der festen Einspannung kann ein links- oder rechtsdrehendes Moment eingezeichnet werden.

Das Ergebnis zeigt dir dann an, ob die von dir angenommene Wirkrichtung stimmt oder nicht. Resultiert nämlich ein negatives Ergebnis, dann wirkt die Kraft bzw. das Moment genau entgegengesetzt.

Beispiel: Wirkrichtung

Nimmst du eine horizontale Auflagerkraft in einem Festlager zum Beispiel nach links gerichtet an und es resultiert ein negatives Ergebnis, dann wirkt diese tatsächlich nach rechts.

Schritt 2: Kräftezerlegung

Für jede Kraft, die einen Winkel aufweist, musst du zunächst eine Kräftezerlegung durchführen. Dazu bestimmst du für die gegebene Kraft den Winkel zur Horizontalen (falls nicht gegeben). Danach legst du die Kraft mit dem Anfangspunkt in ein Koordinatensystem und berechnest mittels Kosinus die x-Komponente und mittels Sinus die y-Komponente. Je nachdem in welche Richtung bzw. in welchem Quadranten die Ausgangskraft liegt, können die Kraftkomponenten in positive oder negative Achsenrichtung zeigen.

Du ersetzt nun die Kraft mit Winkel durch die beiden Kraftkomponenten $F_x$ und $F_y$ .

Schritt 3: Gleichgewichtsbedingungen anwenden

Nachdem du das Tragwerk von den Auflagern frei geschnitten hast und die Kraft/Kräfte (sofern vorhanden) in zwei Komponenten zerlegt hast, kannst du damit beginnen die unbekannten Auflagerkräfte zu berechnen.

Merk’s dir!

Alle horizontalen Kräfte gehen in die Gleichgewichtsbedingung in x-Richtung ein. Hierbei berücksichtigst du alle Kräfte die nach rechts zeigen positiv und alle Kräfte die nach nach links zeigen negativ.

Alle vertikalen Kräfte gehen in die Gleichgewichtsbedingungen in y-Richtung ein. Hierbei berücksichtigst du alle Kräfte die nach oben zeigen positiv und alle Kräfte die nach nach unten zeigen negativ.

Für die Momente gilt, dass diese in der Momentengleichgewichtsbedingung erfasst werden. Alle linksdrehenden Momente sind positiv, alle rechtsdrehenden Momente negativ zu berücksichtigen.

Videoreihen: Auflagerkräfte berechnen

In den folgenden drei Videos zeige ich dir, wie du unbekannte Auflagerkräfte berechnen kannst.

Auflagerkräfte berechnen

Beispiel: Auflagerkräfte berechnen

Im nachfolgenden Beispiel betrachten wir einen belasteten Balken und wollen die Auflagerkräfte berechnen.

Aufgabenstellung

Auflagerkräfte berechnen, Nachhilfe Techniker, Beispiel, Auflagerkräfte, Kräftezerlegung, Balken, Kräfte

Gegeben sei der obige Balken, welcher durch die drei Kräfte F₁, F₂ und F₃ belastet wird. Es gelten die folgenden Größen:

$F_1 = 14 kN$

$F_2 = 26 kN$

$F_3 = 8 kN$

$\alpha = 38^{\circ}$

Berechne die Auflagerkräfte A und B!

Der Balken ist auf einem Loslager A und einem Festlager B gelagert. Wir schneiden zunächst den Balken von seinen Lagern frei.

Schritt 1: Freischnitt

Für das Festlager B tragen wir eine vertikale und eine horizontale Kraft ab, für das Loslager eine vertikale Kraft:

Auflagerkräfte berechnen, Freischnitt, Festlager, Loslager, Balken — Freischnitt der Auflager

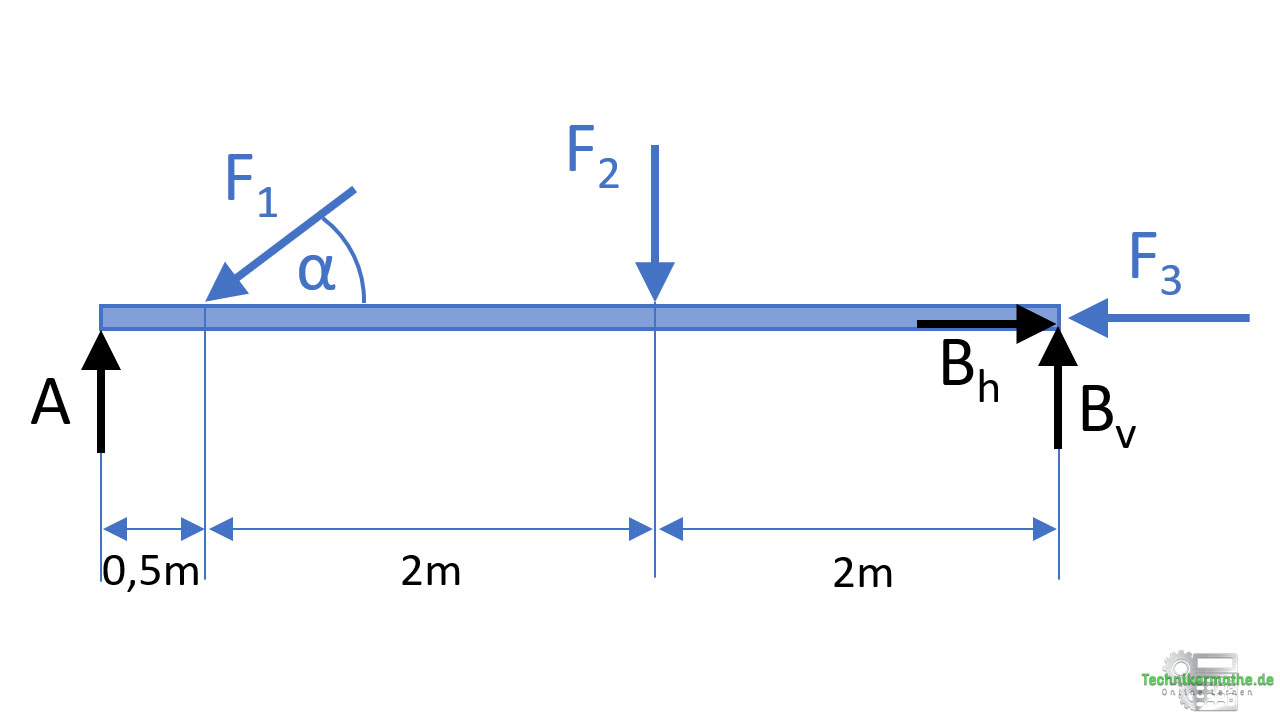
Schritt 2: Kräftezerlegung

Die Kraft F₁ müssen wir in eine x- und eine y-Komponente zerlegen. Da der Winkel zur Horizontalen gegeben ist, verwenden wir den Kosinus für die x-Komponente und den Sinus für die y-Komponente:

$F_{1x} = F_1 \cdot \cos(\alpha) = 14 kN \cdot \cos(38^{circ}) = 11,03 kN$

$F_{1y} = F_1 \cdot \sin(\alpha) = 14 kN \cdot \sin(38^{circ}) = 8,62 kN$

Wir bringen die beiden Kraftkomponenten am Balken an:

Auflagerkräfte berechnen, Kräftezerlegung, Balken, Beispiel — Anbringung der Komponenten der Kraft F1

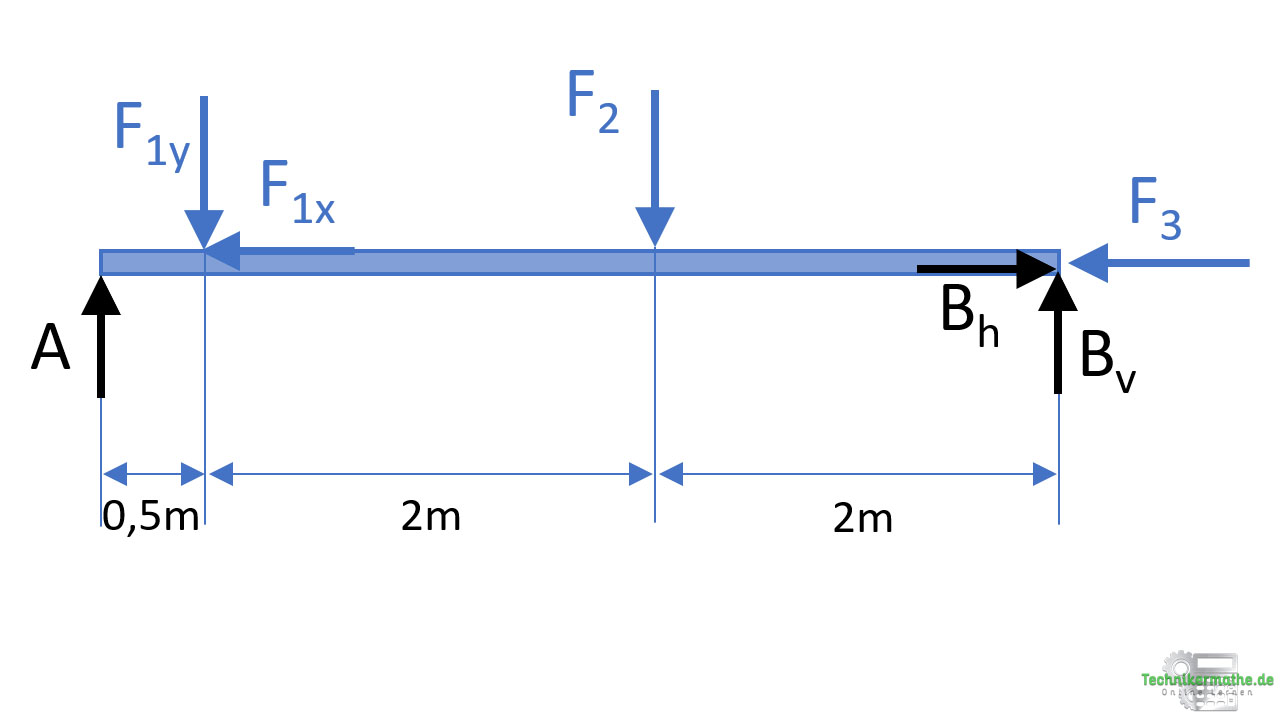
Schritt 3: Gleichgewichtsbedingungen

Im letzten Schritt können wir mittels der drei Gleichgewichtsbedingungen die unbekannten Auflagerkräfte berechnen. Wir starten mit Momentengleichgewichtsbedingung. Den Bezugspunkt legen wir so, dass so viele unbekannte Kräfte wie möglich wegfallen. Also in das Festlager B:

Auflagerkräfte berechnen, Bezugspunkt, Balken, Moment, Momentengleichgewichtsbedingung — Bezugspunkt für die Momentengleichgewichtsbedingung

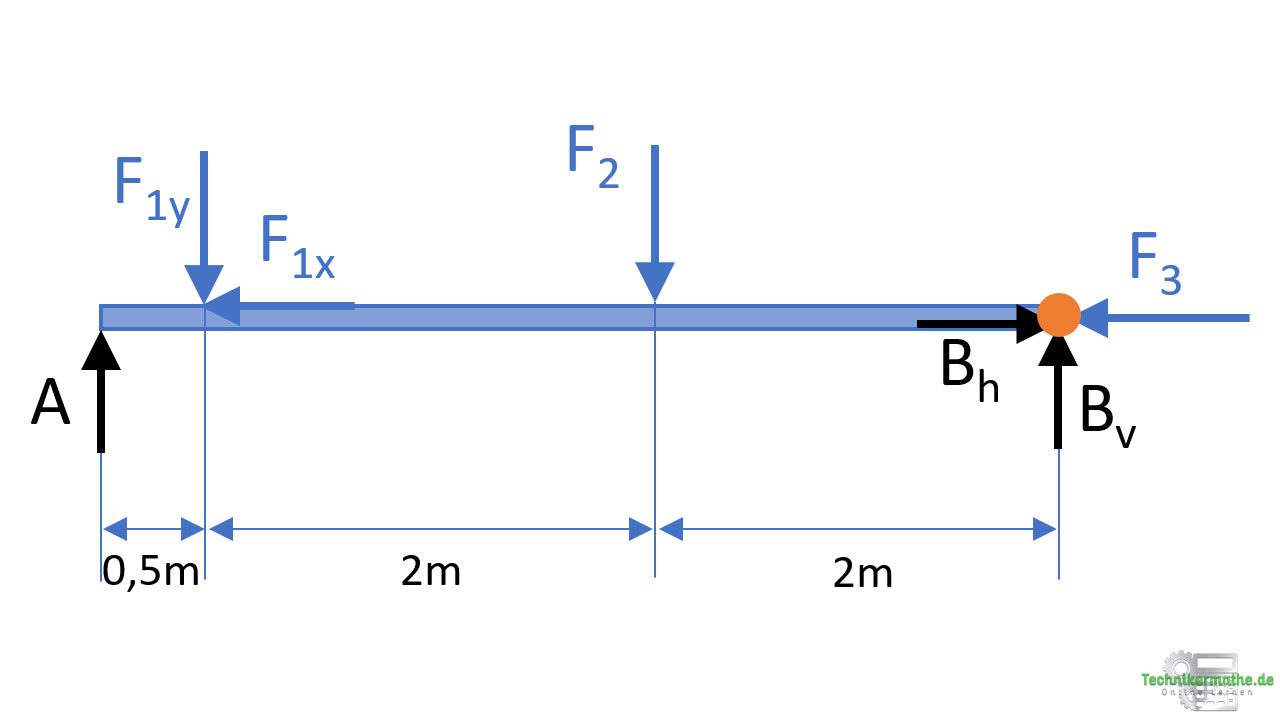
Wir starten mit der Lagerkraft A. Diese weist einen Hebelarm von 4,5 m auf und übt eine Rechtsdrehung (negativ) auf den Bezugspunkt aus. Die Wirkungslinie der Kraft F_1x schneidet den Bezugspunkt, damit ist hier kein Moment auf das Lager B gegeben. Die Kraft F_1y weist einen Hebelarm von 4m und übt ein linksdrehendes Moment auf das Lager B aus. Die Kraft F₂ weist einen Hebelarm von 2m auf und übt ein linksdrehendes Moment aus. Die Kräfte B_v, B_hund F₃ schneiden den Bezugspunkt, damit üben diese kein Moment aus.

Es ergibt sich:

$\sum M^B = 0: \; \; \; -A \cdot 4,5m + F_{1y} \cdot 4m + F_2 \cdot 2m = 0$

Wir können die obige Gleichung nach der unbekannten Lagerkraft A auflösen:

$-A \cdot 4,5m + F_{1y} \cdot 4m + F_2 \cdot 2m = 0$ | $+A \cdot 4,5m$

$F_{1y} \cdot 4m + F_2 \cdot 2m = A \cdot 4,5 m$ bzw.

$A \cdot 4,5m = F_{1y} \cdot 4m + F_2 \cdot 2m$ | $:4,5m$

$A = \dfrac{F_{1y} \cdot 4m + F_2 \cdot 2m}{4,5m}$

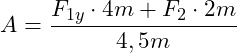
Einsetzen der Werte:

$A = \dfrac{8,62 kN \cdot 4m + 26 kN \cdot 2m}{4,5m}$

$\boxed{A = 19,22 kN}$

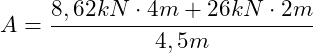
Danach betrachten wir die vertikale Gleichgewichtsbedingung. Hier berücksichtigen wir alle vertikalen Kräfte. Die Kräfte die nach oben zeigen werden positiv berücksichtig, die Kräfte die nach unten zeigen negativ:

$\sum F_{iy} = 0: \; \; \; A - F_{1y} - F_2 + B_v = 0$

Da wir die Lagerkraft A bereits berechnet haben, können wir aus der obigen Gleichung die Lagerkraft B_v berechnen:

$A - F_{1y} - F_2 + B_v = 0$ $|-A | + F_{1y} | + F_2|$

$B_v = -A + F_{1y} + F_2$

Einsetzen der Werte:

$B_v = -19,22 kN + 8,62 kN + 26 kN$

$B_v = 15,4 kN$

Danach betrachten wir die horizontale Gleichgewichtsbedingung. Hier werden alle horizontalen Kräfte berücksichtigt. Kräfte die nach rechts zeigen berücksichtigen wir positiv, Kräfte die nach links zeigen negativ:

$\sum F_{ix} = 0 \; \; \; - F_{1x} -F_3 + B_h = 0$

Auflösen nach der Lagerkraft B_h:

$- F_{1x} -F_3 + B_h = 0$

$B_h = F_{1x} + F_3$

Einsetzen der Werte:

$B_h = 11,03 kN + 8 kN$

$B_h = 19,03 kN$

Wir können die beiden Lagerkräfte B_h und B_v noch zu einer resultierenden Lagerkraft zusammenfassen, indem wir den Satz des Pythagoras anwenden (da beiden Lagerkräfte rechtwinklig zueinander sind):

$B = \sqrt{B_h^2 + B_v^2} =\sqrt{(19,03 kN)^2 + (15,4 kN)^2}$

$B = 24,48 kN$

Was kommt als Nächstes?

In den folgenden Lerneinheiten betrachten weitere ausführliche Beispiele zur Berechnung der unbekannten Auflagerkräfte.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++