Die nachfolgenden Aufgaben sollen dein Verständnis bezüglich der Stromteilerregel verbessern.
Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema. Mehr zu diesem Thema und der Elektrotechnik findest du im Kurs: ET2-Gleichstromtechnik
Aufgabe 1 – Stromteilerregel mit 3 Widerständen
Gegeben ist die nachfolgende Schaltung (Ausschnitt eines Netzwerks):

Als Angabe haben wir die nachfolgenden Werte gegeben:
![]()
![]()
![]()
![]()
Aufgaben:
- Bestimme den Ersatzwiderstand
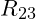
- Bestimme den Strom
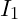
- Verwende die Stromteilerregel um den Strom
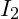 zu bestimmen
zu bestimmen - Verwende die Stromteilerregel um den Strom
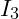 zu bestimmen
zu bestimmen
Bestimme den Ersatzwiderstand R23
Damit wir überhaupt die Stromteilerregel anwenden können, müssen wir im ersten Schritt den Ersatzwiderstand ![]() ermitteln. Dieser errechnet sich über die beiden parallelgeschalteten Widerstände
ermitteln. Dieser errechnet sich über die beiden parallelgeschalteten Widerstände ![]() und
und ![]()
![]()
![]()
![]()
![]()
Bestimme den Strom I1
Im nächsten Schritt benötigen wir für die Anwendung der Stromteilerregel bei Kenntnis der Widerstände zumindest einen Strom. Unsere Wahl fällt auf den Strom ![]() . Diesen können wir mit unseren bisherigen Werten über das Ohm’sche Gesetz berechnen. Berücksichtigen müssen wir, dass sowohl
. Diesen können wir mit unseren bisherigen Werten über das Ohm’sche Gesetz berechnen. Berücksichtigen müssen wir, dass sowohl ![]() als auch
als auch ![]() in die Berechnung eingehen, da sie in Reihe geschaltet sind.
in die Berechnung eingehen, da sie in Reihe geschaltet sind.
![]()
![]()
![]()
![]()
Verwende die Stromteilerregel um den Strom I2 zu bestimmen
Wir wissen, dass sich der Strom auf die Widerstände ![]() und
und ![]() aufteilt. Es gilt:
aufteilt. Es gilt: ![]() und
und ![]() . Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
. Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
![]()
nach ![]() aufgelöst erhalten wir
aufgelöst erhalten wir
![]()
Für eine Bestimmung von ![]() haben wir alle notwendigen Werte gegeben.
haben wir alle notwendigen Werte gegeben.
![]()
![]()
![]()
Verwende die Stromteilerregel um den Strom I3 zu bestimmen
Erneut wiederholen wir den vorherigen Vorgang. Wir wissen noch immer, dass sich der Strom auf die Widerstände ![]() und
und ![]() aufteilt. Es gilt:
aufteilt. Es gilt: ![]() und
und ![]() . Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
. Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
![]()
nach ![]() aufgelöst erhalten wir
aufgelöst erhalten wir
![]()
Für eine Bestimmung von ![]() haben wir alle notwendigen Werte gegeben.
haben wir alle notwendigen Werte gegeben.
![]()
![]()
![]()
Aufgabe 2 – Stromteilerregel mit 4 Widerständen
Gegeben ist die nachfolgende Schaltung (Ausschnitt eines Netzwerks):

Als Angabe haben wir die nachfolgenden Werte gegeben:
![]()
![]()
![]()
![]()
![]()
Aufgaben:
- Bestimme den Ersatzwiderstand
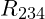
- Bestimme den Strom
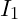
- Verwende die Stromteilerregel um den Strom
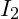 zu bestimmen
zu bestimmen - Verwende die Stromteilerregel um den Strom
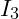 zu bestimmen
zu bestimmen
Bestimme den Ersatzwiderstand R234
Damit wir überhaupt die Stromteilerregel anwenden können, müssen wir im ersten Schritt den Ersatzwiderstand ![]() ermitteln. Dieser errechnet sich über die drei parallelgeschalteten Widerstände
ermitteln. Dieser errechnet sich über die drei parallelgeschalteten Widerstände ![]() ,
, ![]() und
und ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Bestimme den Strom I1
Im nächsten Schritt benötigen wir für die Anwendung der Stromteilerregel bei Kenntnis der Widerstände zumindest einen Strom. Unsere Wahl fällt auf den Strom ![]() . Diesen können wir mit unseren bisherigen Werten über das Ohm’sche Gesetz berechnen. Berücksichtigen müssen wir, dass sowohl
. Diesen können wir mit unseren bisherigen Werten über das Ohm’sche Gesetz berechnen. Berücksichtigen müssen wir, dass sowohl ![]() als auch
als auch ![]() in die Berechnung eingehen, da sie in Reihe geschaltet sind.
in die Berechnung eingehen, da sie in Reihe geschaltet sind.
![]()
![]()
![]()
![]()
Verwende die Stromteilerregel um den Strom I2 zu bestimmen
Wir wissen, dass sich der Strom auf die Widerstände ![]() ,
, ![]() und
und ![]() aufteilt. Es gilt:
aufteilt. Es gilt: ![]() und
und ![]() . Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
. Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
![]()
nach ![]() aufgelöst erhalten wir
aufgelöst erhalten wir
![]()
Für eine Bestimmung von ![]() haben wir alle notwendigen Werte gegeben.
haben wir alle notwendigen Werte gegeben.
![]()
![]()
![]()
Verwende die Stromteilerregel um den Strom I3 zu bestimmen
Erneut wiederholen wir den vorherigen Vorgang. Wir wissen noch immer, dass sich der Strom auf die Widerstände ![]() ,
, ![]() und
und ![]() aufteilt. Es gilt:
aufteilt. Es gilt: ![]() und
und ![]() . Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
. Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
![]()
nach ![]() aufgelöst erhalten wir
aufgelöst erhalten wir
![]()
Für eine Bestimmung von ![]() haben wir alle notwendigen Werte gegeben.
haben wir alle notwendigen Werte gegeben.
![]()
![]()
![]()
Verwende die Stromteilerregel um den Strom I4 zu bestimmen
Erneut wiederholen wir den vorherigen Vorgang. Wir wissen noch immer, dass sich der Strom auf die Widerstände ![]() ,
, ![]() und
und ![]() aufteilt. Es gilt:
aufteilt. Es gilt: ![]() und
und ![]() . Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
. Daraus ergibt sich für die Stromteilerregel folgendes Verhältnis:
![]()
nach ![]() aufgelöst erhalten wir
aufgelöst erhalten wir
![]()
Für eine Bestimmung von ![]() haben wir alle notwendigen Werte gegeben.
haben wir alle notwendigen Werte gegeben.
![]()
![]()
![]()
Mit Hilfe dieser Aufgaben hast du nun hoffentlich einen genauen Überblick zu den Stromteilern und der Stromteilerregel erhalten. Dieses Verzeichnis mit Aufgaben wird fortwährend erweitert.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






