MA4 – Zwei senkrechte Geraden (Beispiel: senkrecht + windschief)

In dieser Lerneinheit behandeln Senkrechte Geraden und wollen dir zeigen, wie du herausfinden kannst, ob die Geraden senkrecht zueinander liegen.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: MA4 – Vektorrechnung

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Senkrechte Geraden – Grundlagen

Zwei zueinander senkrechte Geraden (auch: orthogonale Geraden) sind dann senkrecht zueinander, wenn sie in einem 90°-Winkel zueinander liegen. Zwei senkrechte Gerade in der Ebene schneiden sich immer, zwei senkrechte Geraden im Raum können sich entweder schneiden oder liegen windschief zueinander.

Zwei senkrechte Geraden?

Das Konzept von zwei senkrechten (orthogonalen) Geraden ist ein fundamentales Prinzip in der Geometrie und wird oft in der analytischen Geometrie, Physik und Ingenieurwesen angewendet. Zwei Geraden sind senkrecht zueinander, wenn der Winkel zwischen ihnen 90 Grad beträgt.

Wir betrachten zunächst die Steigungsform (Geraden in der Ebene) und dann die Parameterform (Geraden im Raum) und zeigen dir danach anhand von zwei Beispielen, wie du herausfindest, ob zwei Geraden senkrecht zueinander sind.

Senkrechte Geraden: Steigungsform

Sind zwei Geraden g₁ und g₂ mit ihrer Steigungsform gegeben, so können wir anhand der Steigung erkennen, ob die beiden Geraden senkrecht zueinander stehen:

$g_1 = mx + b$

$g_2 = nx + d$

Hierbei ist m die Steigung der Geraden g₁ und n die Steigung der Geraden g₂.

Sind die beiden Geraden senkrecht ( $\perp$ ) zueinander, so gilt:

Senkrechte Geraden

$g_1 \perp g_2$ :

$m \cdot n = -1$

Multiplizieren wir die beiden Steigungen miteinander und resultiert -1, so sind die beiden Geraden senkrecht zueinander.

Merk’s dir!

Sind zwei Geraden in der Ebene senkrecht zueinander, so besitzen sie einen gemeinsamen Schnittpunkt.

Senkrechte Geraden: Parameterform

Sind zwei Geraden g₁ und g₂ mit ihrer Parameterform gegeben, so können wir anhand der Richtungsvektoren erkennen, ob die beiden Geraden senkrecht zueinander stehen:

$g_1: \vec{x} = \vec{A} + t \cdot \vec{u}$

$g_2: \vec{x} = \vec{B} + s \cdot \vec{n}$

Hierbei ist $\vec{u}$ der Richtungsvektor der Geraden g₁ und $\vec{n}$ der Richtungsvektor der Geraden g₂.

Sind die beiden Geraden senkrecht ( $\perp$ ) zueinander, so gilt:

Senkrechte Geraden

$g_1 \perp g_2$ :

$\vec{u} \cdot \vec{n} = 0$

Bilden wir das Skalarprodukt der beiden Richtungsvektoren und resultiert als Ergebnis 0, so sind die beiden Geraden senkrecht zueinander.

Merk’s dir!

Sind zwei Geraden im Raum senkrecht zueinander, so besitzen sie entweder einen gemeinsamen Schnittpunkt oder liegen windschief zueinander.

Beispiele und Aufgaben

Beispiel: Steigungsform (Ebene)

Beispiel!

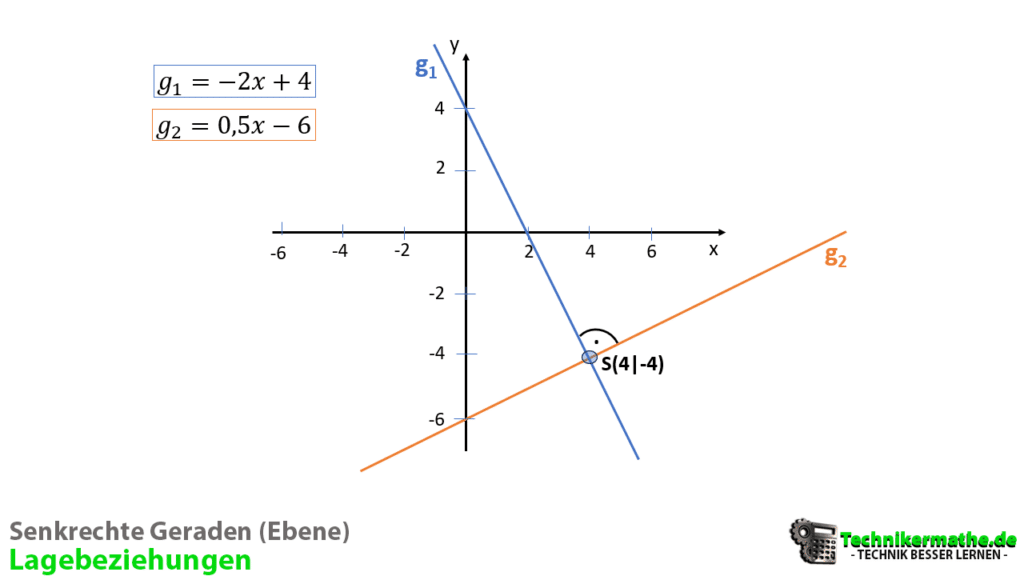
Gegeben seien die beiden Geraden g₁ und g₂ in der Ebene mit ihrer Steigungsform:

$g_1 = -2x + 4$

$g_2 = 0,5x - 6$

Stehen die beiden Geraden senkrecht zueinander? Und wenn ja, in welchem Punkt schneiden sich die beiden Geraden?

Wir können herausfinden, ob die beiden Geraden senkrecht zueinander stehen indem wir die Steigungen miteinander multiplizieren:

$-2 \cdot 0,5 = -1$

Das Ergebnis der Multiplikation ist -1. Demnach stehen die beiden Geraden senkrecht zueinander.

Als nächstes berechnen wir den gemeinsamen Schnittpunkt. Dazu setzen wir die beiden Geraden gleich und berechnen x (siehe auch unseren Kurs MA2-Lineare Funktionen):

$-2x + 4 = 0,5x - 6$

$-2x - 0,5x = -6 - 4$

$-2,5x = -10$

$x = 4$

An der Stelle x = 4 schneiden sich die beiden senkrechten Geraden. Den Schnittpunkt berechnen wir, indem wir x = 4 in eine der Geradengleichungen einsetzen:

$g_1(x = 4) = -2 \cdot 4 +4 = -4$

$g_2(x = 4) = 0,5 \cdot 4 - 6 = -4$

Der gemeinsame Schnittpunkt ist gegeben bei S(4|-4). In der folgenden Grafik siehst du die beiden Geraden mit ihrem Schnittpunkt eingezeichnet:

Senkrechte Geraden, Lagebeziehungen, Steigungsform, Parameterform

Beispiel: Parameterform (Raum)

Beispiel!

Gegeben seien die beiden Geraden g₁ und g₂ im Raum mit ihrer Steigungsform:

$g_1: \vec{x} = \left( \begin{array}{c} 2\\ 0 \\ -1 \end{array}\right) + t \cdot \left( \begin{array}{c} 3 \\ 1 \\ -4 \end{array}\right)$

$g_2: \vec{x} = \left( \begin{array}{c} 0 \\ 4 \\ -2 \end{array}\right) + t \cdot \left( \begin{array}{c} 3 \\ -1 \\ 2 \end{array}\right)$

Stehen die beiden Geraden senkrecht zueinander? Schneiden sich die beiden Geraden?

Wir können herausfinden, ob die beiden Geraden senkrecht zueinander stehen indem wir das Skalarprodukt der beiden Richtungsvektoren bilden:

$\left( \begin{array}{c} 3 \\ 1 \\ -4 \end{array}\right) \cdot \left( \begin{array}{c} 3 \\ -1 \\ 2 \end{array}\right)$

$3 \cdot 3 + 1 \cdot (-1) + (-4) \cdot 2 = 0$

Das Ergebnis der Skalarmultiplikation beträgt 0. Demnach stehen die beiden Geraden senkrecht zueinander. Sind zwei Geraden im Raum senkrecht zueinander, so schneiden diese sich nicht automatisch, sondern können auch windschief zueinander sein. Sie können aber nicht parallel oder identisch sein.

Um herauszufinden, ob die beiden Geraden windschief sind oder einen Schnittpunkt aufweisen, setzen wir die beiden Geradengleichungen gleich:

$\left( \begin{array}{c} 2 \\ 0 \\ -1 \end{array}\right) + t \cdot \left( \begin{array}{c} 3 \\ 1 \\ -4 \end{array}\right) = \left( \begin{array}{c} 0 \\ 4 \\ -2 \end{array}\right) + s \cdot \left( \begin{array}{c} 3 \\ -1 \\ 2 \end{array}\right)$

Dann stellen wir das lineare Gleichungssystem auf:

$(1) \; 2 + 3t = 0 + 3s$

$(2) \; 0 + 1t = 4 - 1s$

$(3) \; -1 - 4t = -2 + 2s$

Wir haben nun ein lineares Gleichungssystem mit zwei Unbekannten gegeben. Hier können wir das Gleichsetzungs-, Einsetzungs- oder Additionsverfahren anwenden.

Schauen wir uns das Gleichungssystem an und fassen soweit wie möglich zusammen:

$(1) \; 2 + 3t = 3s$

$(2) \; t = 4 - s$

$(3) \; -1 - 4t = -2 + 2s$

Wir benötigen zwei Gleichungen, da wir zwei Unbekannte gegeben haben. Das Gleichsetzungsverfahren ist grundsätzlich am Einfachsten anzuwenden. Hier stellen wir einfach zwei der drei Gleichungen nach derselben Variable (hier t oder s) um und setzen diese beiden Gleichungen gleich. Wir stellen beliebig die 2. und 3. Gleichung nach t um:

$(2) \; t = 4 - s$

$(3) \; -1 - 4t = -2 + 2s$

$t = \frac{1}{4} - \frac{1}{4}s$

Gleichsetzen von (2) und (3):

$4-s = \frac{1}{4} - \frac{1}{4}s$

Nach s auflösen:

$-s +\frac{1}{4}s = \frac{1}{4} -4$

$-\frac{3}{4}s = -\frac{15}{4}$

$s = 5$

Wir haben für s = 5 erhalten. Als nächstes berechnen wir aus einer dieser beiden Gleichungen (2) oder (3) den Wert t:

(2) $t = 4 - s = 4 - 5 = -1$

Wir haben nun die Gleichung (2) und (3) verwendet, um s = 5 und t = -1 zu erhalten. Die dritte nicht verwendete Gleichung (hier: (1)) nutzen wir, um die Ergebnisse zu überprüfen. Dazu setzen wir t = -1 und s = 5 ein und schauen, ob die Gleichung erfüllt ist (d.h. beide Seiten gleich sind):

$(1) \; 2 + 3 \cdot (-1) = 3 \cdot 5$

$(1) \; -1 \neq 15$

Die Gleichung ist nicht erfüllt, damit ist hier kein Schnittpunkt gegeben. Die beiden Geraden sind demnach senkrecht und windschief zueinander.

Anwendung senkrechter Geraden

Geometrische Konstruktionen: Zeichnen von orthogonalen Linien, z.B. Achsen in einem Koordinatensystem.
Physik: Bestimmung von Normal- und Tangentialkräften.
Ingenieurwesen: Berechnung von orthogonalen Schnittpunkten in Strukturen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was bedeutet es, wenn zwei Geraden senkrecht sind?

Sie schneiden sich im rechten Winkel (90 Grad).

2. Wie überprüfe ich, ob zwei Geraden senkrecht sind?

Überprüfe, ob das Skalarprodukt ihrer Richtungsvektoren null ist oder ob das Produkt ihrer Steigungen $-1$ ergibt.

3. Kann ich die Senkrecht-Bedingung in drei Dimensionen anwenden?

Ja, die Bedingung $\vec{d}_1 \cdot \vec{d}_2 = 0$ gilt auch im dreidimensionalen Raum.

4. Gibt es eine einfache geometrische Methode, senkrechte Geraden zu finden?

Ja, zeichne die Geraden und überprüfe visuell, ob der Winkel zwischen ihnen 90 Grad beträgt.

5. Wie wirkt sich die Senkrecht-Bedingung auf parallele Geraden aus?

Parallele Geraden können nicht senkrecht zueinander sein, da sie sich nicht schneiden.

Zusammenfassung

Das Konzept der senkrechten Geraden ist ein grundlegendes Prinzip der Geometrie. Zwei Geraden sind senkrecht zueinander, wenn sie sich im rechten Winkel schneiden, was mathematisch durch das Produkt ihrer Steigungen $- 1$ oder ein Skalarprodukt von null ihrer Richtungsvektoren bestätigt wird.

Dieses Prinzip findet in vielen wissenschaftlichen und technischen Anwendungen Verwendung und ist ein wichtiger Bestandteil der analytischen Geometrie.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++