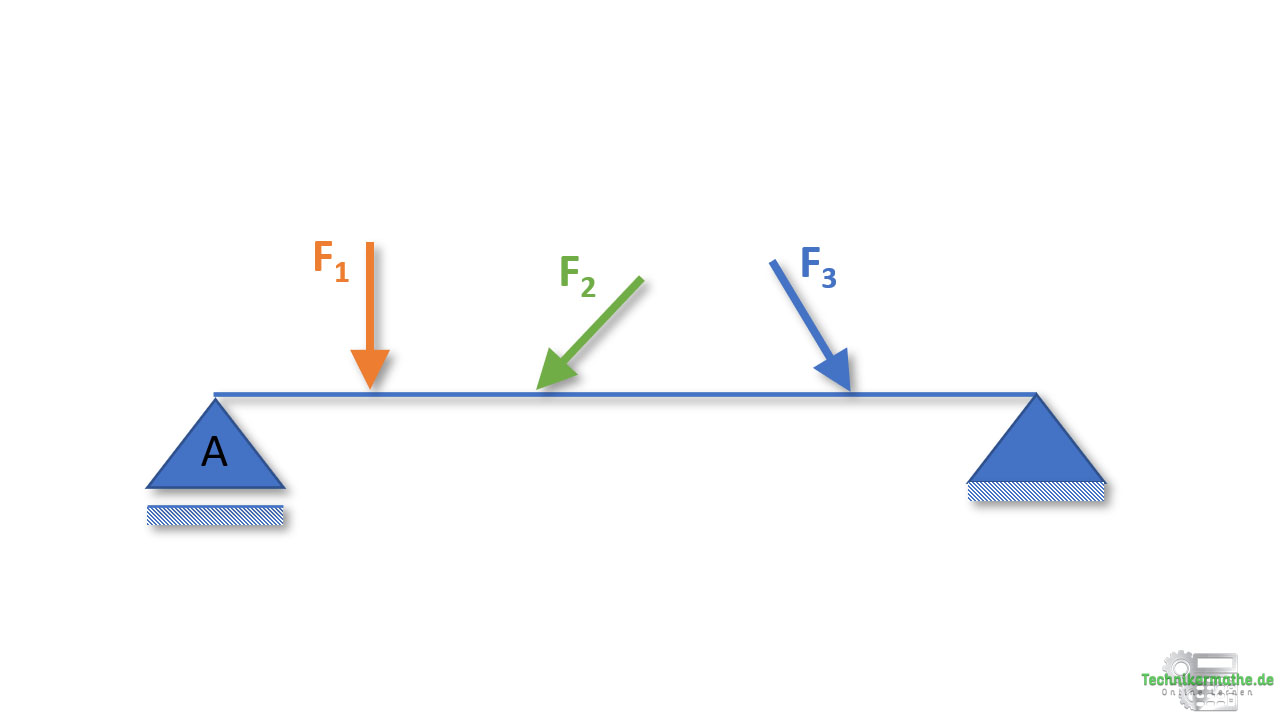
Das Seileckverfahren dient der grafischen Bestimmung der Lage einer resultierenden Kraft (Angriffspunkt). Es ist die Grundvoraussetzung für die Anwendung des Culmann-Verfahrens zur grafischen Ermittlung der unbekannten Lagerkräfte und des Cremonaplans zur grafischen Bestimmung von unbekannten Stabkräften
Für ein optimales Verständnis helfen dir ein Videoclip und zwei anschauliche Rechenbeispiele zu dem Thema.
Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.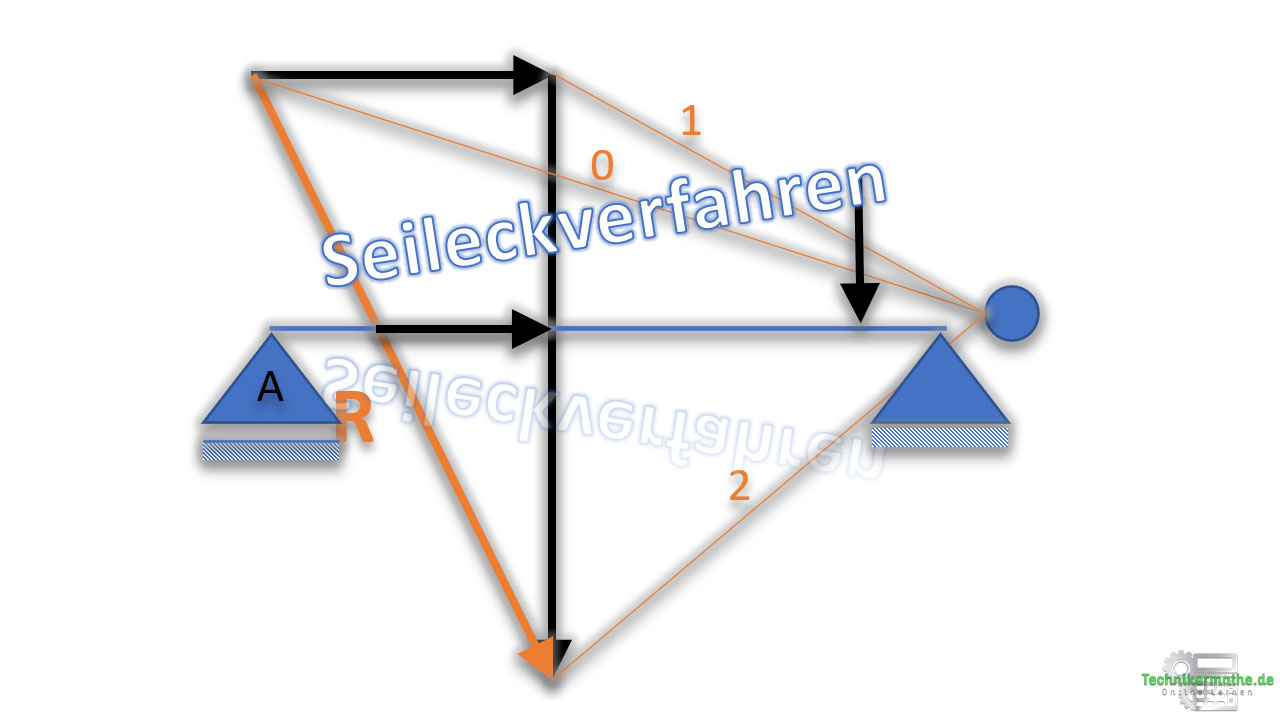
Das Seileckverfahren dient der grafischen Bestimmung der Lage einer resultierenden Kraft (Angriffspunkt).
Das Seileckverfahren ist die Grundvoraussetzung für die Anwendung des Culmann-Verfahrens zur grafischen Ermittlung der unbekannten Lagerkräfte und des Cremonaplans zur grafischen Bestimmung von unbekannten Stabkräften. Beide Verfahren werden in den folgenden Lerneinheiten behandelt.
++ Videoclip – Seileckverfahren ++
Im folgenden Video zeige ich dir mit Hilfe eines Prüfungsbeispiels wie das Seileckverfahren funktioniert.
Beispiel: Seileckverfahren
Schauen wir uns mal an einem Beispiel an, wie das Seileckverfahren funktioniert.
Gegeben sei der obige Balken, welcher durch drei äußere Kräfte belastet wird.
Wir wollen für diese drei äußeren Kräfte die Resultierende R bestimmen. Dazu benötigen wir den Betrag, die Richtung und die Lage der Resultierenden, da wir uns im allgemeinen Kräftesystem befinden.
Betrag und Richtung der Resultierenden
Wir starten damit den Betrag und die Richtung der Resultierenden mittels grafischer Vektoraddition (siehe vorherige Lerneinheit) zu bestimmen. Zunächst müssen wir dazu einen geeigneten Maßstab festlegen.
Maßstab:
5 kN = 1cm
Wir führen dann die grafische Vektoraddition der drei Kräfte durch und bestimmen die Resultierende:
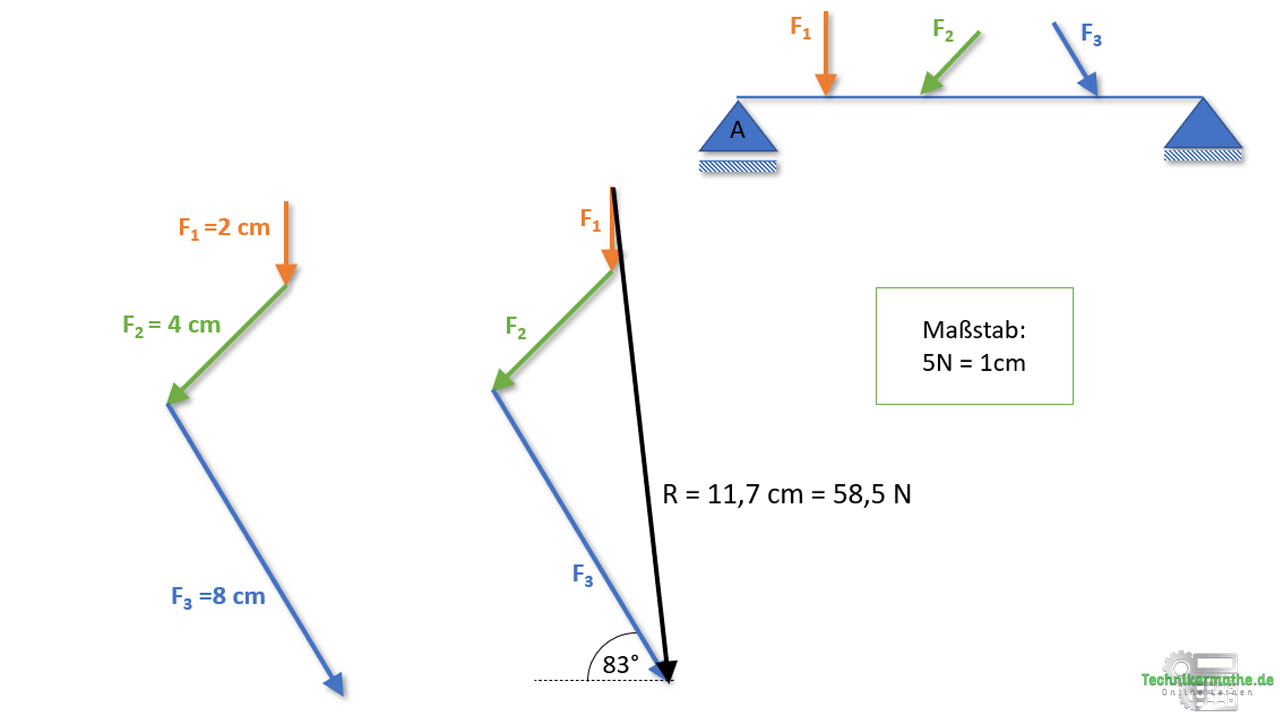
Nach Messung der Länge der Resultierenden erhalten wir einen Betrag von:
Die Richtung wird bestimmt, indem der Winkel von der Resultierenden zur Horizontalen mittels Geodreieck abgetragen wird. Hier erhalten wir ungefähr:
Je nachdem wie genau du die Kräfte eingezeichnet hast, können die berechneten Werte ein wenig abweichen.
Lage der Resultierenden
Wo genau greift die Resultierende an dem Balken an? Diese Frage können wir mittels Seileckverfahren beantworten. Ausgangspunkt des Seileckverfahrens ist die grafische Vektoraddition inklusive eingezeichneter Resultierenden (siehe oben).
Polstrahlen ermitteln
Wo genau greift die Resultierende an dem Balken an? Diese Frage können wir mittels Seileckverfahren beantworten. Ausgangspunkt des Seileckverfahrens ist die grafische Vektoraddition inklusive eingezeichneter Resultierenden.
Wir legen jetzt einen beliebigen Punkt fest, von welchem wir Polstrahlen zu den Anfangspunkten der Kräfte zeichnen. Diese Polstrahlen müssen wir nummerieren, weil wir sie später auf den Balken übertragen müssen.
Wir starten immer bei der zuerst verwendeten Kraft (hier: F1) und ziehen nun einen Polstrahl 0 vom festgelegten Punkt zum Anfangspunkt der Kraft. Danach betrachten wir die nächste Kraft und ziehen einen Polstrahl 1 zum Anfangspunkt der nächsten Kraft (F2) und der Polstrahl 2 zum Anfangspunkt der Kraft F3. Nachdem alle äußeren Kräfte betrachtet wurden, ziehen wir noch einen Polstrahl 3 zur Spitze der Resultierenden. Das ganze sieht dann wie folgt aus:
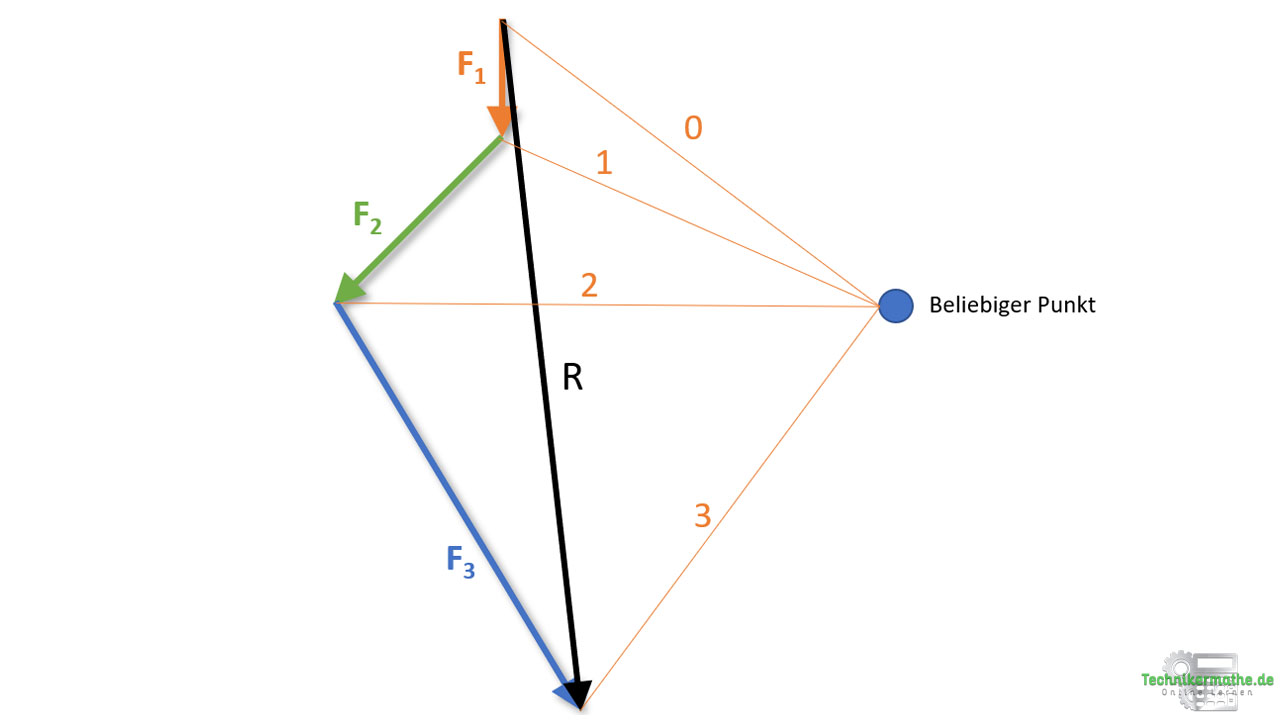
Nachdem wir die Polstrahlen bestimmt haben, können wir diese als nächstes nach und nach auf den Balken übertragen, um die Lage der Resultierenden zu bestimmen. Wir können hier wieder vom Ausgangsbeispiel ausgehen, wir benötigen also nicht den obigen Maßstab, weil wir nur die Wirkungslinien betrachten. Die Größe der Resultierenden haben wir bereits bestimmt.
Polstrahlen einzeichnen
Schritt 1: Zunächst müssen wir die Wirkungslinien der äußeren Kräfte am Balken verlängern:
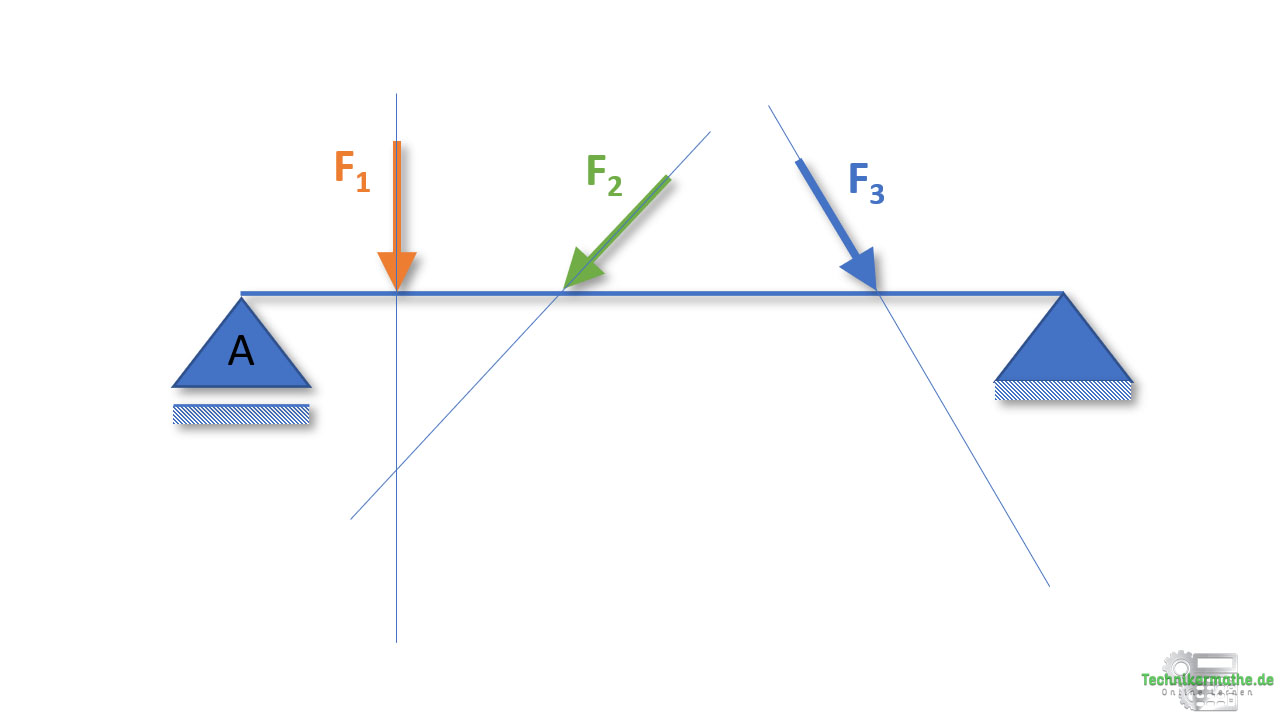
Schritt 2: Als nächsten fügen wir den Polstrahl 0 ein. Der Polstrahl 0 berührt die Kraft F1. Deswegen fügen wir ihn so ein, dass dieser sich mit der Wirkungslinien der Kraft F1 schneidet. Wo genau sich Polstrahl 0 und Wirkungslinie der Kraft F1 schneiden ist für den ersten Polstrahl 0 beliebig. Wichtig ist nur, dass die Richtung des Polstrahls 0 nicht verändert wird.
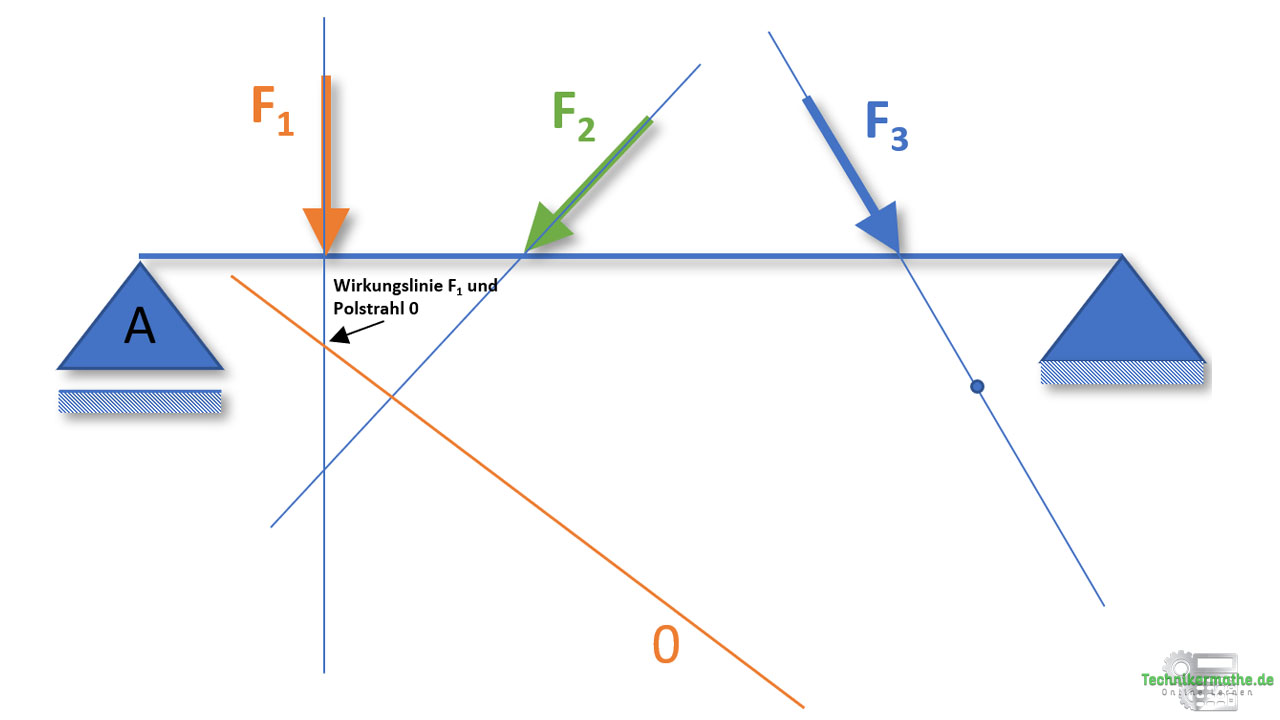
Schritt 3: Als nächsten fügen wir den Polstrahl 1 ein. Der Polstrahl 1 berührt die Kraft F1 und die Kraft F2. Deswegen fügen wir ihn so ein, dass dieser sich mit der Wirkungslinien der Kraft F1 und F2 schneidet. Den Polstrahl 1 müssen wir nun in den Schnittpunkt von Polstrahl 0 und F1 legen, damit haben wir den Schnittpunkt von Polstrahl 0 und 1 gegeben (0,1). Der Pohlstrahl 1 schneidet dann ganz von alleine die Wirkungslinie Kraft F2 (falls nicht verlängere den Polstrahl).
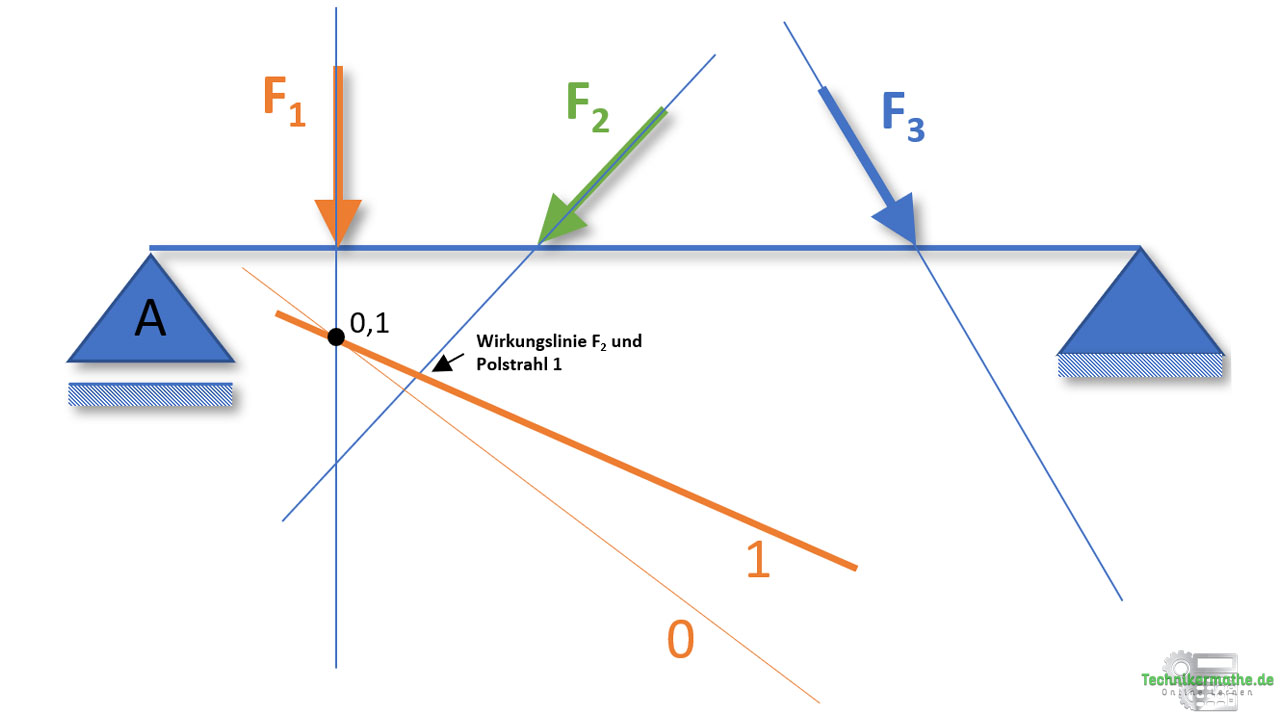
Schritt 4: Als nächsten fügen wir den Polstrahl 2 ein. Der Polstrahl 2 berührt die Kraft F2 und die Kraft F3. Deswegen fügen wir ihn so ein, dass dieser sich mit der Wirkungslinien der Kraft F2 und F3 schneidet. Den Polstrahl 2 müssen wir nun in den Schnittpunkt von Polstrahl 1 und F2 legen, damit haben wir den Schnittpunkt von Polstrahl 1 und 2 gegeben (1,2). Der Pohlstrahl 2 schneidet dann ganz von alleine die Wirkungslinie Kraft F3 (falls nicht verlängere den Polstrahl).
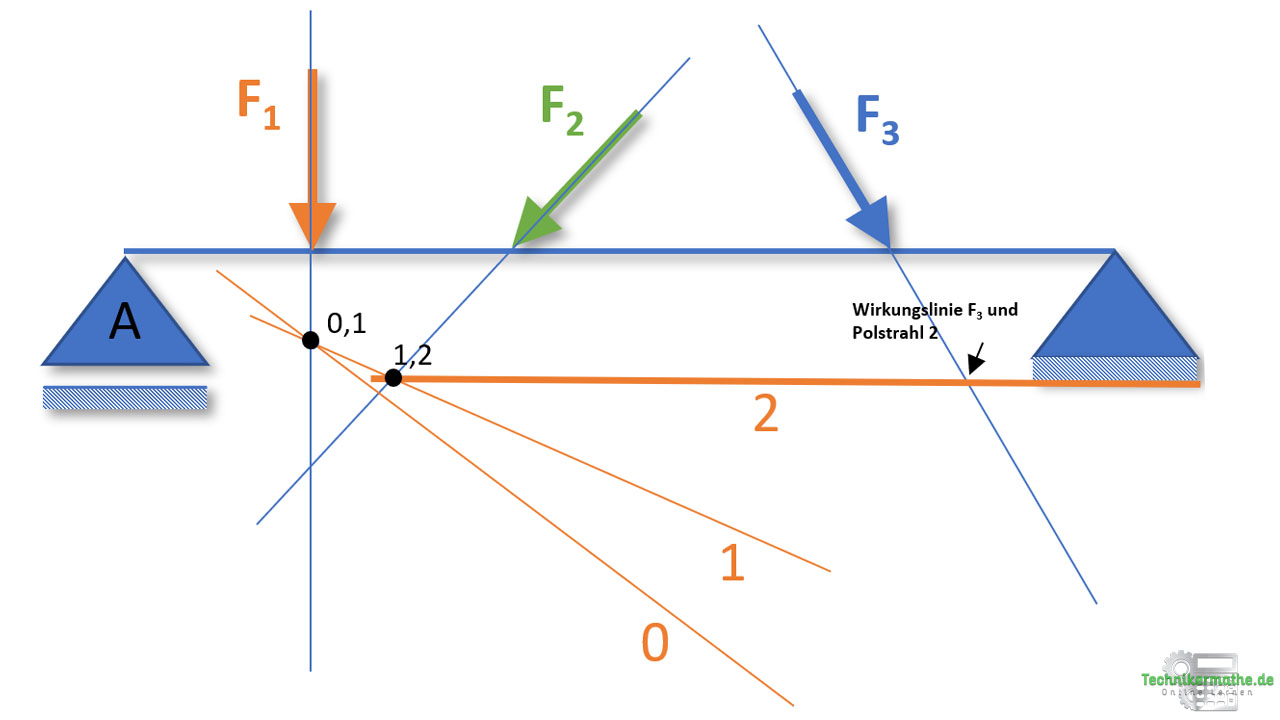
Schritt 4: Als nächsten fügen wir den Polstrahl 3 ein. Der Polstrahl 3 berührt die Kraft F3. Deswegen fügen wir ihn so ein, dass dieser sich mit der Wirkungslinien der Kraft F3 schneidet. Den Polstrahl 3 müssen wir nun in den Schnittpunkt von Polstrahl 2 und F3 legen, damit haben wir den Schnittpunkt von Polstrahl 2 und 3 gegeben (2,3).
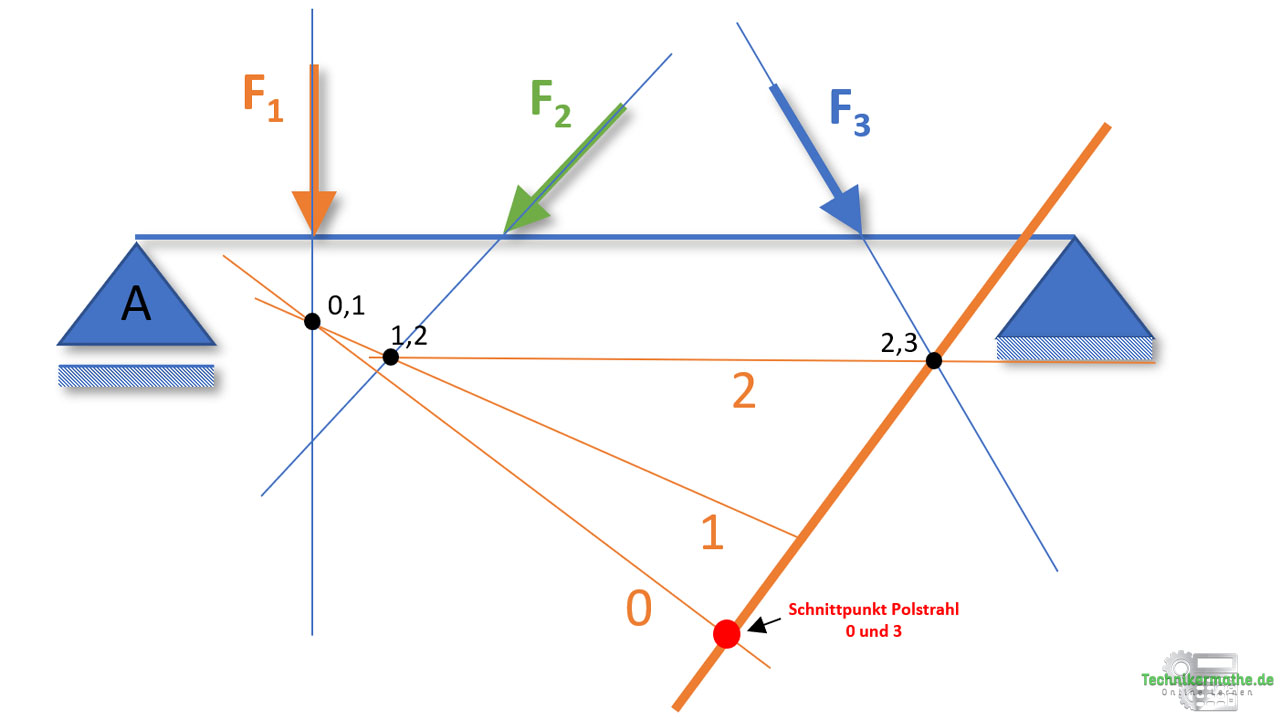
Du hast nun alle Polstrahlen berücksichtigt. Die Lage der Resultierenden befindet sich dabei im Schnittpunkt von Polstrahl 0 und 3 (0,3). Auch hier müssen die Polstrahlen gegebenenfalls verlängert werden.
Resultierende einzeichnen
Das Ergebnis sieht wie folgt aus:
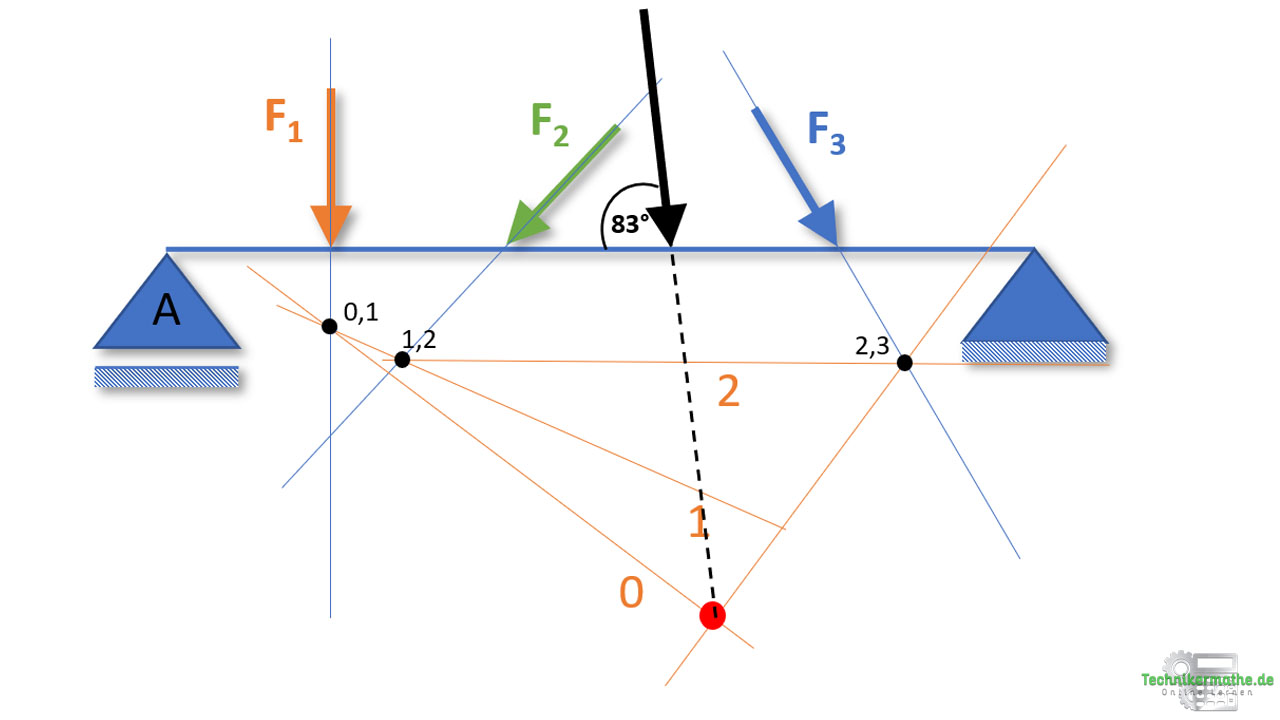
Die Wirkungslinien der Resultierende wird mit ihrer oben bestimmten Richtung (Winkel von 83° zur Horizontalen) in den Schnittpunkt des Polstrahls 0 und 3 eingetragen und dann auf ihrer Wirkungslinie so weit verschoben, bis diese oben am Balken angreift.
Die Resultierende liegt immer im Schnittpunkt des ersten und letzten Polstrahls. Bei mehr als 3 Kräften sind demnach auch mehr Polstrahlen gegeben. Bei 4 Kräften sind zum Beispiel 5 Postrahlen (von 0 bis 4) gegeben. Hier liegt die Resultierende im Schnittpunkt von Polstrahl 0 und 4.
In der folgenden Lerneinheit betrachten wir das Culmann-Verfahren zur grafischen Bestimmung der Auflagerkräfte. Das hier behandelte Seileckverfahren ist Grundvoraussetzung für die Anwendung des Culmann-Verfahrens.
Ein weiteres Beispiel zum Seileckverfahren folgt bei der Anwendung des Cremonaplans sowie innerhalb der Probeklausur.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben
Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team