PH4 – Energieverlust | Reibungsverlust [Grundlagen, Beispiele, Aufgaben]

In dieser Lerneinheit behandeln wir den Energieverlust infolge von Reibungskräften (auch: Reibungsverluste).

Für ein optimales Verständnis helfen dir zwei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Kinetik findest du im Kurs: PH4-Kinetik

Energieverlust – Definition

Ein Energieverlust bezieht sich auf den Verlust von Energie innerhalb eines Systems oder bei der Umwandlung von einer Energieform in eine andere.

Energieverlust, Reibungsverlust, Reibungsverluste, Reibung, Energie, Verlust — Reibungsverlust

Es gibt verschiedene Arten von Energieverlusten, die in unterschiedlichen Situationen auftreten können.

Reibungsverlust: Reibung ist ein weiterer wichtiger Faktor, der zu Energieverlusten führen kann. Wenn zwei Oberflächen aneinander reiben, wird ein Teil der Energie in Form von Wärmeenergie dissipiert. Dies kann beispielsweise bei der Bewegung von Fahrzeugen auf Straßen oder bei rotierenden Teilen in Maschinen auftreten.
Wärmeenergieverlust: Einer der häufigsten Energieverluste ist der Verlust von Wärmeenergie. Dies tritt auf, wenn Energie in Form von Wärme an die Umgebung abgegeben wird. Zum Beispiel kann ein Teil der Energie, die in einem Verbrennungsmotor erzeugt wird, als Abwärme verloren gehen, anstatt in mechanische Arbeit umgewandelt zu werden.
Leitungs- und Übertragungsverluste: Bei der Übertragung von elektrischer Energie über Kabel oder Leitungen kommt es zu Verlusten. Diese Verluste entstehen durch den elektrischen Widerstand des Leiters, was zu einer Umwandlung von elektrischer Energie in Wärme führt. Je länger die Strecke und je höher der Stromfluss, desto größer sind die Leitungs- und Übertragungsverluste.
Strahlungsverlust: Bei bestimmten Energieumwandlungsprozessen, wie z.B. in Heizungs- oder Beleuchtungssystemen, kann Energie in Form von elektromagnetischer Strahlung verloren gehen. Diese Strahlung wird oft nicht effizient genutzt und trägt zum Energieverlust bei.
Ineffiziente Umwandlung: Bei der Umwandlung von einer Energieform in eine andere kann es zu Verlusten kommen. Beispielsweise können bei der Umwandlung von elektrischer Energie in mechanische Energie in einem Elektromotor Verluste auftreten, die als Verluste in Form von Wärmeenergie resultieren.

Energieverluste sind unvermeidlich und treten in Energieumwandlungsprozessen aufgrund verschiedener physikalischer Effekte auf. Die Reduzierung von Energieverlusten ist ein wichtiger Aspekt der Energieeffizienz und wird in vielen Bereichen angestrebt, um den Energieverbrauch zu minimieren und die Nachhaltigkeit zu verbessern.

Energieverlust durch Reibung

Es tritt immer dann Reibung auf, wenn Körper aufeinander haften, gleiten oder rollen. Die Kräfte die zwischen den Körpern wirken werden als Reibungskräfte bezeichnet. Die wirkenden Reibungskräfte sind immer so gerichtet, dass sie der Bewegung entgegenwirken und damit die Bewegung hemmen oder sogar verhindern (Haftung).

Grund für das Entstehen von Reibungskräfte ist die Oberflächenbeschaffenheit von Körpern. Je rauer ein Körper ist, desto mehr Reibung tritt auf.

Merk’s dir!

Ein Körper auf einem gefroren See weist demnach weniger Reibung auf, als ein Körper auf einer gepflasterten Straße.

Energieverlust – Formeln

Reibungskräfte verrichten längs eines Weges s eine Reibungsarbeit W_R:

$W_R = F_R \cdot s$

Die Reibungskraft wird wie folgt aus der Normalkraft berechnet:

$F_R = \mu \cdot F_N = \mu \cdot m \cdot g \cdot cos(\alpha)$

Diese Reibungsarbeit führt zu einem Verlust an mechanischer Energie in derselben Höhe:

Reibungsverlust

$E_{reib} = F_R \cdot s$

mit

$F_R$ Reibungskraft

$s$ Weg

Wir können diesen Energieverlust auch als Reibungsverlust E_reib bezeichnen. Die mechanische Energie eines Systems wird also durch Reibung reduziert.

Schauen wir uns dazu mal ein Beispiel an.

Hinweis!

Für das folgende ausführliche Beispiel benötigst du die Gleichungen für die Berechnungen an der schiefen Ebene (Reibungskraft und Normalkraft).

Energieverlust durch Reibung

Wir schauen uns im Folgenden zwei Beispiele zur Berechnung von Energieverlusten infolge auftretender Reibungskräfte an.

Beispiel 1: Energieverlust und schiefe Ebene

Aufgabenstellung

Reibungsverlust, Energieverlust, schiefe Ebene — Reibungsverlust

Eine Kiste mit der Masse m = 100 kg liegt auf einer schiefen Ebene (s = 7,73m, h = 2m). Der Reibungskoeffizient beträgt μ = 0,15. Der Neigungswinkel α = 15°.

Welche kinetische Energie weist der Körper am Ende der schiefen Ebene auf?

Zunächst berechnen wir die potentielle Energie des Körpers. Hierzu müssen wir die senkrechte Höhe h = 2m heranziehen:

$E_{pot} = m \cdot g \cdot h = 100 kg \cdot 9,81 \dfrac{m}{s^2} \cdot 2m = 1.962 J$

Was passiert ohne Reibung?

Die Kiste rutscht die schiefe Ebene herab. Dabei wandelt sich die potentielle Energie vollständig in kinetische Energie um. Am Ende der schiefen Ebene weist also die Kiste eine kinetische Energie auf von:

$E_{kin} = E_{pot} = 1.962 J$

Was passiert mit Reibung?

Der Körper rutscht die schiefe Ebene herab. Dabei tritt Reibung zwischen der Kiste und der schiefen Ebene auf. Der Reibungskoeffizient beträgt μ=0,15. Die Reibungskraft beträgt damit:

$F_R = \mu \cdot F_N$

$F_N = m \cdot g \cdot \cos(\alpha) = 100 kg \cdot 9,81 \dfrac{m}{s^2} \cdot \cos(15^\circ) = 947,57 N$

$F_R = 0,15 \cdot 947,57 N = 142,14 N$

Infolge der Reibungskraft wird Reibungsarbeit verrichtet, die auch gleichzeitig den Energieverlust angibt:

$W_{reib} = E_{reib} = F_R \cdot s$

$W_{reib} = E_{reib} = 142,14 N \cdot 7,73 m = 1.098,74 J$

Der Energieverlust beträgt damit 1.098,74 Joule. Die kinetische Energie am Ende der schiefen Ebene ist in diesem Fall nicht mehr gleich der potentiellen Energie am Beginn der schiefen Ebene, da durch die Reibung Energie verloren geht. Die Reibung führt dazu, dass die Energie in Wärmeenergie umgewandelt wird, welche dann an die Umgebung abgegeben wird. Für die Berechnung der kinetischen Energie müssen wir also den Energieverlust berücksichtigen:

$E_{kin} = E_{pot} - E_{reib} = 1.962 J - 1.098,74 J = 863,26 J$

Am Ende der schiefen Ebene weist die Kiste noch kinetische Energie in Höhe von 863,26 Joule auf.

Beispiel 2: Reibungsverluste bei ebener Strecke

Aufgabenstellung

Ein Auto ( m = 1.500 kg) fährt mit konstanter Geschwindigkeit von 100 km/h, als plötzlich der Motor ausfällt.

Wie weit (in Meter) kann das Auto rollen, wenn der Reibungskoeffizient mit μ= 0,15 gegeben ist?

Das Auto weist fährt mit der Geschwindigkeit von 80 km/h, als der Motor ausfällt. Danach rollt das Auto. Zunächst berechnen wir die SI-Einheiten:

$100\dfrac{km}{h} : 3,6 = 27,78 \dfrac{m}{s}$

Wir können jetzt die kinetische Energie bestimmen, die das Auto zu Beginn des Rollens besitzt:

$E_{kin} = \dfrac{1}{2} \cdot m \cdot v^2 = \dfrac{1}{2} \cdot 1.500 kg \cdot (27,78 \dfrac{m}{s})^2 = 578.796,3 J$

Das Auto kommt dann zum Stehen, wenn die kinetische Energie und die Reibungsverluste gleich groß sind. Dann steht das Auto, da es keine Bewegungsenergie mehr aufweist. Die kinetische Energie wurde dann komplett in Wärmeenergie umgewandelt und an die Umgebung abgegeben.

Wir müssen nun also die Reibungsverluste und die kinetische Energie gleich setzen:

$E_{reib} = E_{kin} = 578.796,3 J$

Die Reibungsverluste werden wie folgt berechnen:

$E_{reib} = F_R \cdot s$

$F_R \cdot s = 578.796,3 J$

Gesucht ist hier der Weg s, bei welchem kinetische Energie und Reibungsenergie gleich groß sind und das Auto zum Stehen kommt. Dafür müssen wir aber erst die Reibungskraft FR berechnen:

$F_R = \mu \cdot F_N$

Die Normalkraft ist bei einer horizontalen Ebene gleich der Gewichtskraft:

$F_N = F_G = m \cdot g = 1.500 kg \cdot 9,81 \dfrac{m}{s^2} = 14.715 N$

$F_R = 0,15 \cdot 14.715 N = 2.207,25 N$

Einsetzen in die obige Gleichung ergibt:

$2.207,25 N \cdot s = 578.796,3 J$

Auflösen nach s:

$s = \dfrac{578.796,3 J}{2.207,25 N} = 262,23 m$

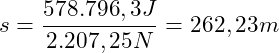
Nachdem der Motor ausfällt rollt das Auto noch einen Weg von 262,23 Meter und kommt dann zum Stehen.

Was kommt als Nächstes?

Nachdem du jetzt den Energieverlust durch Reibung, also den Reibungsverlust kennengelernt hast, behandeln wir in der folgenden Lerneinheit die Spannenergie.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++