(Ph4-17) kinetische Energie – Beispiele und Berechnung

In dieser Lerneinheit behandeln wir die kinetische Energie, die auch als Bewegungsenergie bezeichnet wird.

Für ein optimales Verständnis helfen dir zwei Videoclips und zwei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Physik findest du im Kurs: PH4-Kinetik

Kinetische Energie: Grundlagen

Merk’s dir!

Ein Körper, der sich in Bewegung befindet, besitzt die Fähigkeit Arbeit zu verrichten. Deswegen wird die kinetische Energie auch als Bewegungsenergie bezeichnet.

Kinetische Energie ist die Energie, die ein Objekt aufgrund seiner Bewegung besitzt. Sie hängt von der Masse des Objekts und seiner Geschwindigkeit ab.

Je größer die Masse eines Objekts ist und je schneller es sich bewegt, desto mehr kinetische Energie hat es.

Die kinetische Energie eines Objekts wird durch die Arbeit erzeugt, die auf das Objekt ausgeübt wird. Arbeit wird geleistet, wenn eine Kraft auf ein Objekt über eine bestimmte Strecke hinweg wirkt. Die Arbeit wird dann in kinetische Energie umgewandelt.

Kinetische Energie – Beispiele im Alltag

Hier sind einige Beispiele für die Nutzung von kinetischer Energie im Alltag:

Beispiel!

Ein Auto, das sich auf der Straße bewegt, hat kinetische Energie. Diese Energie wird verwendet, um das Fahrzeug voranzutreiben und es in Bewegung zu halten.
Wenn du Fahrrad fährst, wird die kin. Energie in deinen Beinen durch das Treten der Pedale erzeugt. Diese Energie treibt das Fahrrad an und ermöglicht es dir, dich fortzubewegen.
Wenn du einen Ball wirfst, hat er kin. Energie, die ihm erlaubt, sich durch die Luft zu bewegen.
Ein Ventilator verwendet elektrische Energie, um sich zu drehen und kinetische Energie zu erzeugen, die Luft in einem Raum zu bewegen und für Kühlung zu sorgen.
Ein Kinderkarussell verwendet kin. Energie, um sich zu drehen. Die Kinder sitzen auf den sich bewegenden Sitzen und genießen die Fahrt.
Eine Achterbahn verwendet die kin. Energie, um die Wagen durch Loopings und steile Abfahrten zu beschleunigen und den Fahrgästen ein aufregendes Erlebnis zu bieten.
Wenn du auf einer Schaukel schaukelst, wird die kinetische Energie durch deine Bewegung erzeugt und treibt dich in immer höhere Schwingungen.

Diese sind nur einige Beispiele für die Nutzung von kinetischer Energie im Alltag. Es gibt viele weitere Anwendungen, bei denen kinetische Energie eine wichtige Rolle spielt.

kinetische Energie eines Windrades [Windkonverter]

Wir haben hier bereits das Beispiel mit dem Wasserkraftwerk (Lerneinheit: Potentielle Energie) kennengelernt. Das bewegte Wasser weist kinetische Energie auf und kann durch die Bewegungsenergie eine Turbine antreiben. Das bewegte Wasser besitzt also die Fähigkeit Arbeit zu verrichten (= eine Turbine zu betreiben).

Ein weiteres Beispiel aus der Praxis für den Gebrauch von kinetischer Energie ist eine Windkraftanlage. Hier wird die bewegte Luft (=Wind) dazu genutzt, die Rotorblätter des Windrades zu betreiben. Dadurch wird ein Generator betrieben, welcher die Bewegungsenergie in elektrische Energie umwandelt. Wenn wir von einem reibungsfreien Prozess ausgehen, dann wird die gesamte Windenergie (kinetische Energie) in elektrische Energie umgewandelt.

Gut zu wissen!

In der Praxis unterliegen alle Energieumwandlungen energetischen Verlusten / Reibungsverlusten. Bei der Umwandlung von Windenergie in elektrische Energie liegt der Wirkungsgrad bei ca. 40%. Das bedeutet, dass ca. 40% der Windenergie (kinetische Energie) am Ende in elektrische Energie umgewandelt werden kann.

Kinetische Energie – Formel / Einheit

Ein bewegter Körper weist eine gewisse Geschwindigkeit und damit kinetische Energie auf. Du kannst die kinetische Energie über die folgende Gleichung berechnen:

$\boxed{W_{kin} = \frac{1}{2} \cdot m \cdot v^2}$ Kinetische Energie

Die Einheit der kinetischen Energie ist Joule [J].

Merk’s dir!

$1 J = 1 Nm = \dfrac{kg m}{s^2} m$

Die kinetische Energie eines sich bewegenden Körpers hängt von seiner Masse m und seiner Geschwindigkeit v ab. Sie ist umso größer,

je größer die Masse (m) des Körpers ist und
je größer seine Geschwindigkeit (v) ist.

Videoclip: Kinetische Energie aus Beschleunigungsarbeit

In dem folgenden Video zeigen wir dir, wie du die Formel für diese Energie aus der Beschleunigungsarbeit herleiten kannst:

Lernclip

Kinetische Energie: Formel

Energieumwandlung: Kinetische und potentielle Energie

Potentielle und kinetische Energie im Wechsel

Wir wollen uns mal den Zusammenhang zwischen kinetischer und potentieller Energie anschauen. Nehmen wir als Beispiel das Jonglieren von Bällen. Als Bezugsniveau wählen wir die Hand des Jongleurs, die sich idealerweise immer in derselben Höhe befindet. Die Höhe der Hand wählen wir also als Referenz. Zur Beschreibung der Energieumwandlung betrachten wir nur den ersten abgeworfenen Ball, für die anderen gilt dasselbe Prinzip. Wir gehen auch davon aus, dass keine Reibung auftritt. Du wirst nun also den ersten Ball nach oben.

Was passiert?

Unmittelbar nach dem Abwurf besitzt der Ball nur kinetische Energie, weil er noch keine Höhe gewonnen hat. Sobald der Ball anfängt zu steigen, nimmt der Ball an Höhe zu und damit steigt auch seine potentielle Energie. Je höher der Ball fliegt, desto mehr nimmt die potentielle Energie zu und die kinetische Energie ab (der Ball wird langsamer). Hier findet die Umwandlung von kinetische in potentielle Energie statt.

Ist der Ball an seinem höchsten Punkt angekommen, besitzt er nur noch potentielle Energie und keine kinetische Energie mehr (der Ball steht kurz in der Luft, bevor er wieder fällt). An diesem Punkt ist die potentielle Energie gleich der kinetischen Energie unmittelbar nach dem Abwurf.

Der Ball fällt – infolge der Erdanziehung – wieder nach unten. Hier erfolgt die Umwandlung von potentielle in kinetische Energie. Je mehr der Ball an Höhe verliert, desto weniger potentielle Energie und desto mehr kinetische Energie besitzt er. Kurz bevor der Ball wieder in deiner Hand landet, besitzt der Ball nur noch kinetische Energie und keine potentielle Energie mehr. Sobald der Ball wieder in deiner Hand liegt, besitzt er weder potentielle noch kinetische Energie – in Bezug auf deine Hand natürlich. Denn in Bezug auf den Boden zum Beispiel besitzt der Ball natürlich potentielle Energie.

Videoclip: potentielle und kinetische Energie + Wirkungsgrad

Im folgenden Video zeigt dir Jan nochmal einen Überblick über die pot. und kin. Energie sowie den Wirkungsgrad:

Lernclip

Potentielle und kinetische Energie

Schauen wir uns mal einige Beispiele zur Berechnung der kinetischen Energie an.

Beispiele: Energie

In den folgenden Beispielen behandeln wir die kinetische und potentielle Energie unter Vernachlässigung von Reibung. Versuche zunächst die Aufgaben selbstständig zu lösen, bevor du dir die Lösungen anschaust. Du benötigst zum Lösen der Aufgaben die folgenden Gleichungen:

$E_{kin} = \dfrac{1}{2} \cdot m \cdot v^2$

$E_{pot} = m \cdot g \cdot h$

$E_{spann} = \dfrac{1}{2} \cdot D \cdot s^2$

Beispiel 1 : Energie berechnen

Aufgabenstellung

Ein Auto mit einem Gewicht von 2 Tonnen fährt mit einer Geschwindigkeit von 50 km/h.

Wie groß ist seine kinetische Energie?

Lösung

Bevor du die Berechnung durchführst, musst du die gegebenen Einheiten in SI-Einheiten umrechnen:

2 t = 2.000 kg

50 km/h = 13,89 m/s

Die Umrechnung von km/h in m/s erfolgt über den Faktor 3,6. Danach können die Werte in die Gleichung der kinetischen Energie eingesetzt werden:

$E_{kin} = \frac{1}{2} \cdot m \cdot v^2 = \frac{1}{2} \cdot 2.000 kg \cdot 13,89 \dfrac{m}{s} = 13.890 J$

Die kinetische Energie beträgt 13.890 Joule.

Beispiel 2: Geschwindigkeit berechnen

Aufgabenstellung

Du lässt aus 2m Höhe einen Ball reibungsfrei aus dem Fenster fallen (freier Fall).

Welche Geschwindigkeit kann der Ball maximal erreichen?

Lösung

Um diese Aufgaben zu lösen benötigen wir die kinetische und potentielle Energie. Wir haben also einen Ball in der Hand, welcher sich in einer senkrechten Höhe 2m über dem Boden befindet. Der Ball weist also (vor dem Fallenlassen) potentielle Energie auf. Die Gleichung lautet:

$E_{pot} = m \cdot g \cdot h$

Danach lässt du den Ball fallen. Die potentielle Energie wird dann in Bewegungsenergie umgewandelt. Unmittelbar beim Aufprall auf den Boden besitzt der Ball keine potentielle Energie mehr, da diese vollständig in Bewegungsenergie umgewandelt wurde. Hier ist die kinetische Energie maximal und entspricht der potentiellen Energie vor dem Loslassen. Die Gleichung für die kinetische Energie beträgt:

$E_{kin} = \dfrac{1}{2} \cdot m \cdot v^2$

Da die kinetische Energie unmittelbar beim Aufprall gleich der potentiellen Energie vor dem Loslassen ist, gilt:

$E_{pot} = E_{kin}$

$m \cdot g \cdot h = \dfrac{1}{2} \cdot m \cdot v^2$

Wir suchen die Geschwindigkeit und können die obige Gleichung nach der Geschwindigkeit v auflösen:

$m \cdot g \cdot h = \dfrac{1}{2} \cdot m \cdot v^2$ | $:m$

$g \cdot h = \dfrac{1}{2} \cdot v^2$ | $\cdot 2$

$2 \cdot g \cdot h = v^2$ | $\sqrt{}$

$\sqrt{2 \cdot g \cdot h} = v$

Wir können jetzt die gegebenen Werte einsetzen:

$\sqrt{2 \cdot 9,81 \dfrac{m}{s^2} \cdot 2m} = v$

$v = 6,26 \dfrac{m}{s}$

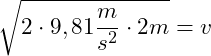
Die maximale Geschwindigkeit des Körpers unmittelbar beim Aufprall beträgt 6,26 m/s also 22,54 km/h.

Was kommt als Nächstes?

In der nächsten Lerneinheit behandeln wir die Reibungsenergie.

Was gibt es noch bei uns?

Tausende interaktive Übungsaufgaben

Übungsbereich

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Das erwartet dich!

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Auszüge aus unserem Kursangebot!

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

building 4794329 1280 — TM1 (Technische Mechanik – Kurs)

scientist 6621069 1280 — WT3 (Werkstoffprüfung – Kurs)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 7,40 EUR/Monat
++ Besser geht’s nicht!! ++