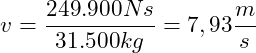Impuls – Definition
Ein Impuls bezieht sich in der Physik auf die Menge an Bewegung eines Körpers. Er wird definiert als das Produkt aus der Masse m des Körpers und seiner Geschwindigkeit v. Der Impuls ist eine vektorielle Größe, was bedeutet, dass er sowohl eine Größe als auch eine Richtung hat. Gemäß dem Impulserhaltungssatz bleibt die Gesamtmenge an Impuls in einem isolierten System konstant, solange keine äußeren Kräfte wirken.

Der Impuls eines Körpers ist umso größer, je schneller es sich bewegt und je mehr Masse er aufweist. Umgangssprachlich bezeichnen wir die Größe häufig mit Wucht oder Schwung.
Erhaltungsgröße: Der Impuls eines Körpers bleibt – unabhängig von inneren Vorgängen – konstant, sofern keine äußeren Kräfte auf den Körper einwirken.
Impuls – Beispiele im Alltag
Hier sind einige Beispiele für Impuls im Alltag:
-
Stoß beim Billardspiel: Beim Billardspiel erhält der Spielball einen Impuls, wenn er von der Queuekugel getroffen wird. Der Impuls wird dann auf die anderen Kugeln übertragen, wodurch sie in Bewegung versetzt werden.
-
Absprung beim Springen: Beim Springen oder Hüpfen übt eine Person einen Impuls auf den Boden aus, um sich nach oben abzustoßen. Je größer der Impuls, desto höher ist der Sprung.
-
Raketenstart: Bei einem Raketenstart wird Treibstoff verbrannt und ausgestoßen, was eine nach unten gerichtete Kraft erzeugt und der Rakete einen Impuls nach oben verleiht. Dies ermöglicht der Rakete, sich gegen die Schwerkraft zu bewegen und ins All zu gelangen.
-
Abprallen eines Balls: Wenn ein Ball auf eine harte Oberfläche trifft, wird er mit einer entgegengesetzten Richtung und Geschwindigkeit reflektiert. Der Impuls des Balls ändert sich aufgrund der Kraft, die während des Aufpralls auf den Ball wirkt.
Diese Beispiele zeigen, wie der Impuls im Alltag eine Rolle spielt, insbesondere bei der Beschreibung von Bewegungen und Wechselwirkungen zwischen Körpern.
Impuls – Formelzeichen, Richtung und Größe
Das Formelzeichen des Impulses ist das p (Lateinisch: pellere; Deutsch: stoßen).
Die SI-Einheit ist:
Der Impuls ist eine vektorielle Größe und weist somit einen Betrag (eine Größe) und eine Richtung auf. Dabei fallen die Richtung des Impulses mit der Bewegungsrichtung des Körpers zusammen (beide zeigen in die gleiche Richtung). Der Betrag des Impulses kann wie folgt berechnet werden:
Der Impuls p ist das Produkt aus der Masse des Körpers (m) und der Geschwindigkeit (v) seines Massenmittelpunktes.
Translationsbewegung
Der Impuls eines Körpers betrachtet nur die Translationsbewegung seines Massenmittelpunktes. Eine mögliche auftretende Rotation des Körpers wird nicht durch den Impuls sondern durch den Drehimpuls beschrieben.
Die Translationsbewegung bezieht sich auf eine Bewegung, bei der ein Körper in gerader Linie ohne Rotation oder Drehung voranschreitet. Bei einer Translationsbewegung bewegt sich der gesamte Körper als Ganzes, wobei alle Punkte des Körpers denselben Weg zurücklegen und dieselbe Geschwindigkeit haben.
Die Translationsbewegung kann in zwei Arten unterteilt werden: Die lineare Translationsbewegung und die gekrümmte Translationsbewegung.
-
Lineare Translationsbewegung: Bei der linearen Translationsbewegung bewegt sich ein Körper entlang einer geraden Linie. Alle Punkte des Körpers haben denselben Weg und dieselbe Geschwindigkeit. Ein Beispiel für eine lineare Translationsbewegung ist ein Auto, das auf einer geraden Straße vorwärts fährt.
-
Gekrümmte Translationsbewegung: Bei der gekrümmten Translationsbewegung bewegt sich ein Körper auf einer gekrümmten Bahn, beispielsweise auf einem Kreis oder einer Kurve. Obwohl die Bewegung eine gekrümmte Bahn beschreibt, handelt es sich dennoch um eine Translationsbewegung, da alle Punkte des Körpers denselben Weg zurücklegen und dieselbe Geschwindigkeit haben. Ein Beispiel für eine gekrümmte Translationsbewegung ist ein Auto, das eine enge Kurve auf einer Straße durchfährt.
Die Translationsbewegung kann durch verschiedene Faktoren beeinflusst werden, wie zum Beispiel durch die auf den Körper ausgeübten Kräfte, die Masse des Körpers und den Reibungswiderstand. Die Bewegung eines Körpers kann durch die Anwendung der Newton’schen Gesetze der Bewegung erklärt werden.
Translationsbewegungen spielen eine wichtige Rolle im Alltag und in verschiedenen Anwendungen, wie zum Beispiel im Transportwesen, bei der Bewegung von Fahrzeugen, beim Laufen, Gehen oder Fliegen von Lebewesen sowie bei mechanischen Systemen wie Förderbändern oder Linearführungen.

Bei der Translation bewegt sich ein Körper auf einer geraden Linie oder auf einer beliebig gekrümmten Bahn im Raum. Dabei bewegen sich alle Massepunkte des Körpers parallel zueinander.
Ein Beispiel wäre zum Beispiel die Bewegung eines Fahrzeugs. Alle Teile (Punkte) des Fahrzeugs bewegen sich parallel zueinander. In der obige Grafik siehst du ein Auto, welches sich nach rechts bewegt.
Die Punkte auf dem Auto bewegen sich alle parallel zueinander, also mit demselben Abstand in derselben Zeit.
In der obigen Grafik sind dazu zwei beliebige Punkte angegeben, die aufzeigen, dass sich die Punkte parallel zueinander bewegen. So bewegt sich das hintere Heck ein gewisse Strecke über eine bestimmte Zeit. Der hintere Reifen legt dieselbe Strecke in derselben Zeit zurück.
Damit du nachvollziehen kannst, was die Größe auszeichnet und wie du diese berechnen kannst, schauen wir uns mal einige Beispiele an.
Beispiele: Impuls berechnen
Es folgen einige Beispiel zur Anwendung der Impulsgleichung. Wir betrachten hier zunächst einen Körper. Versuche die Aufgaben selbstständig zu lösen, bevor du dir die Lösungen anschaust.
Beispiel 1 : Fußball
Ein Fußball mit einer Masse von m = 225 g fliegt mit einer Geschwindigkeit von 120 km/h in Richtung Tor.
Welchen Impuls besitzt der Fußball, wenn wir den Luftwiderstand vernachlässigen?
Wir können hier ganz einfach die Impulsgleichung heranziehen, um den Impuls zu berechnen:
Wir benötigen dazu die SI-Einheiten der Masse [kg] und der Geschwindigkeit [m/s]. Dazu rechnen wir die gegebenen Einheiten um:
Wir können nun die Werte in die Gleichung einsetzen:
Der Fußball weist einen Impuls von 7,5 Newtonsekunden auf.
Beispiel 2: Eisenbahnwaggon
Betrachten wir einen offenen Waggon einer Eisenbahn. Der Waggon weist eine Masse von 30 Tonnen auf und bewegt sich mit einer Geschwindigkeit von 30 km/h. Es beginnt zu regnen, wodurch der offene Waggon sich mit Wasser füllt. Insgesamt sammelt sich eine Wassermasse von 1,5 Tonnen an. Reibungskräfte sind zu vernachlässigen.
Wie groß ist die Geschwindigkeit des Waggons nach dem Regen?
Der erste Schritt ist die Umrechnung der gegebenen Werte in SI-Einheiten:
Danach müssen wir zunächst den Impuls des Waggons vor Beginn des Regens berechnen:
Nach dem Regen weist der Waggon eine zusätzliche Masse von 1.500 kg auf, also insgesamt 31.500 kg. Der Wert bleibt konstant, damit ergibt sich:
Die Geschwindigkeit wird gesucht, also stellen wir die Gleichung nach v um:
Der Waggon bewegt sich nach dem Regen mit einer Geschwindigkeit von 7,93 m/s. In diesem Beispiel gehen wir einmal davon aus, dass keine Reibung (Luftreibung, Bodenreibung) auftritt, die den Waggon abbremsen. Wir stellen uns das so vor, dass der Waggon sich mit konstanter Geschwindigkeit bewegt, ohne dass irgendwelche äußeren Kräfte auf den Waggon wirken. In der Realität ist dies natürlich auf der Erde nicht gegeben, da hier Reibungskräfte wirken, die den Waggon abbremsen.
Impulserhaltungssatz – Definition
Der Impulserhaltungssatz besagt, dass der Gesamtimpuls eines mechanisch abgeschlossenen Systems konstant ist. Von einem mechanisch abgeschlossenen System ist die Rede, wenn das System nicht in Wechselwirkung mit seiner Umgebung steht.
Impulserhaltungssatz – Beispiele im Alltag
Hier sind einige Beispiele für den Impulserhaltungssatz im Alltag:
-
Billardspiel: Beim Stoßen eines Billardballs gegen einen anderen Ball beobachten wir, dass der Gesamtimpuls des Systems aus beiden Bällen vor und nach der Kollision konstant bleibt. Der Impuls wird zwischen den Bällen übertragen, sodass der Gesamtimpuls erhalten bleibt.
-
Raketenstart: Beim Start einer Rakete wird Treibstoff mit großer Geschwindigkeit nach unten ausgestoßen. Gemäß dem Impulserhaltungssatz bewirkt die nach unten gerichtete Ausstoßgeschwindigkeit des Treibstoffs eine nach oben gerichtete Beschleunigung der Rakete.
-
Ballfangtrick: Bei einem Trick, bei dem eine Person einen Ball fängt, während sie auf einem drehbaren Stuhl sitzt und diesen in entgegengesetzter Richtung dreht, kann der Impulserhaltungssatz beobachtet werden. Wenn die Person den Ball fängt, dreht sich der Stuhl in die entgegengesetzte Richtung, um den Impuls auszugleichen.
Diese Beispiele zeigen Situationen im Alltag, in denen der Impulserhaltungssatz beobachtet werden kann. Der Impulserhaltungssatz ist ein fundamentales Konzept in der Physik und ermöglicht die Untersuchung von Bewegungen und Kollisionen in verschiedenen Systemen.
Impulserhaltungssatz – Formel
Betrachten wir zwei Körper, die aufeinander einwirken, bleibt der Gesamtimpuls beider Körper (Summe der Impulse beider Körper) konstant. Der Impuls jedes einzelnen Körpers kann sich dabei ändern, die Summe der Einzelimpulse hingegen ist konstant.
mit:
folgt
Dabei ist p1 der Impuls des Körpers 1 und p2 der Impuls des Körpers 2.
Eindimensionaler Stoß zweier Körper
Betrachten wir mal ein Beispiel, um den Impulserhaltungssatz zu verstehen. Nehmen wir einmal an, zwei Körper bewegen sich eindimensional (auf einer Linie) mit einer konstanten Geschwindigkeit aufeinander zu. Wir betrachten der Einfachheit halber zwei Massenpunkte. Der Massenpunkt 1 weist eine Geschwindigkeit v1 auf, der Massenpunkt 2 eine Geschwindigkeit v2. Beide Massenpunkte prallen zusammen und stoßen sich dann voneinander ab, so dass die beiden Massenpunkte sich nach dem Zusammenstoß in entgegengesetzter Richtung mit den Geschwindigkeiten u1 und u2 weiter bewegen.

In der obigen Grafik ist das Beispiel aufgezeigt. Wir haben hier einmal die Geschwindigkeiten v1 und v2 vor dem Aufprall gegeben und außerdem die Geschwindigkeiten u1 und u2 nach dem Aufprall. Der Impulserhaltungssatz ergibt sich in diesem Fall wie folgt:
Die Summe der beiden Impulse vor dem Stoß ist gleich der Summe der beiden Impulse nach dem Stoß.
Dazu stellen wir uns einen Stoß zweier Körper vor. Wir können uns das ganze am Beispiel Billard vorstellen. Das Spiel nutzt den Impuls einer Kugel, um diesen auf eine andere Kugel zu übertragen. Der Gesamtimpuls beider Kugeln ist vor und nach dem Zusammenstoß ist gleich groß (wenn wir die Reibung zwischen Kugel und Billardtisch vernachlässigen). Allerdings haben sich die Einzelimpulse der beiden Kugeln verändert. Trifft die angestoßene Kugel auf eine andere Kugel, dann gibt diese einen Teil ihres Impulses an die andere Kugel ab. Die Summe der beiden Impulse entspricht aber der Summe der Impulse vor dem Stoß.
Auch hier gehen wir wieder davon aus, dass sämtliche Reibungskräfte vernachlässigt werden.
Videos: Impulserhaltungssatz
Schauen wir uns mal die folgenden Videos zum Impulserhaltungssatz an.
Video 1: Impulserhaltungssatz – Erklärung
Video 2: Impulserhaltungssatz – Beispielaufgabe
Schauen wir uns zum Impulserhaltungssatz mal einige Beispiele an.
Beispiele zum Impulserhaltungssatz
Wir betrachten als nächstes einige Beispiele zum Impulserhaltungssatz. Versuche zunächst die Aufgaben selbstständig zu lösen, bevor die die Lösungen zur Hilfe nimmst.
Beispiel 1 : Kugel und Kiste
Impuls vor dem Zusammenstoß
Wir müssen in diesem Beispiel den Impulserhaltungssatz anwenden. Wir schauen uns zunächst die beiden Einzelimpulse von Kugel und Kiste an. Die Kugel hat ein Gewicht von 8 g und bewegt sich vor dem Zusammenprall mit einer Geschwindigkeit von 350 m/s. Wählen wir die Kugel als Körper 1, dann gilt:
Der Impuls der Kugel beträgt vor dem Zusammentreffen 2,8 Ns.
Die Kiste besitzt eine Masse von 2 kg und weist vor dem Zusammenprall keine Geschwindigkeit auf. Es gilt:
Die Kiste weist demnach einen Impuls von Null auf, da sie sich in Ruhe befindet.
Der Gesamtimpuls ist jetzt die Summe der Einzelimpulse:
Der Gesamtimpuls vor dem Zusammenstoß beträgt 2,8 Ns.
Impuls nach dem Zusammenstoß
Was passiert nach dem Zusammenstoß? Beide Körper (Kugel und Kiste) sind zu einem Körper verschmolzen, da die Kugel in der Kiste steckt. Dieser zusammengesetzte Körper muss den Impuls von 2,8 Ns aufweisen, da der Gesamtimpuls konstant bleibt. Die Masse des Körpers ist nichts anderes, als die Summe der beiden Massen (m = 2,008 kg). Die Geschwindigkeit, mit welcher sich dieser Körper bewegt soll berechnet werden:
Der Impuls ist der Gesamtimpuls vor dem Stoß mit 2,8 Ns, die Masse ist die Summe der Masse beider Körper:
Die Gleichung lösen wir nach der gesuchten Geschwindigkeit auf:
Die Kiste mit der Kugel weist nach dem Zusammenstoß eine Geschwindigkeit von 1,39 m/s auf. Dies entspricht einer Geschwindigkeit von 5 km/h (= 1,39 · 3,6).
Beispiel 2: Waggons
Ein Waggon mit einer Masse von 10 Tonnen fährt mit 10 km/h und stößt dabei auf einen zweiten Waggon mit der Masse von 15 Tonnen. Der zweite Waggon bewegt sich in die gleich Richtung, hat aber nur eine Geschwindigkeit von 4 km/h.
Mit welcher Geschwindigkeit fahren beide Waggons nach dem Zusammenprall weiter?
Diese Aufgabe ist fast identisch zur oberen Aufgabe. Dieses Mal weisen aber beide Körper (Waggons) eine Geschwindigkeit auf und fahren in dieselbe Richtung auf derselben Schiene. Da der hintere Waggon aber schneller ist, stößt er irgendwann gegen den vorderen Waggon. Wir starten damit den Gesamtimpuls der beiden Waggons vor dem Stoß zu bestimmen. Du musst vorher noch die Einheiten umrechnen:
Geschwindigkeiten
10 km/h = 10 : 3,6 = 2,78 m/s
4 km/h = 4 : 3,6 = 1,11 m/s
Massen
10 t = 10.000 kg
15 t = 15.000 kg
Gesamtimpuls vor dem Stoß
Als nächstes berechnen wir die Einzelimpulse der beiden Waggons:
Hinterer Waggon:
Vorderer Waggon:
Der Gesamtimpuls ist nichts anderes als die Summe der beiden Einzelimpulse:
Gesamtimpuls nach dem Stoß
Dieser Gesamtimpuls ist auch nach dem Stoß vorhanden. Wir wissen, dass beide Waggons sich gemeinsam bewegen, also eine Geschwindigkeit aufweisen. Du kannst also nach dem Stoß die beiden Körper als ein Körper betrachten, der die Masse der beiden Waggons aufweist:
Und damit gilt:
Wir lösen die Gleichung nach auf und erhalten:
Die beiden Waggons fahren mit einer Geschwindigkeit von 1,8 m/s gemeinsam weiter.
Schnellere Variante
Die schnellere Berechnungsvariante ergibt sich aus der obigen Formeln für den Impulserhaltungssatz:
Da sich beide Waggons nach dem Stoß mit einer Geschwindigkeit (nennen wir sie u) bewegen, gilt:
Wir können die Geschwindigkeit u auf der rechten Seite ausklammern und erhalten:
Danach teilen wir durch die Klammer, damit u alleine steht:
Jetzt können wir alle Werte eingeben und erhalten:
Wir erhalten natürlich dieselbe Geschwindigkeit nach dem Stoß.
Beispiel 3: Zusammenstoß Auto
Ein Auto mit einer Masse von 1200 kg fährt mit einer Geschwindigkeit von 20 m/s. Es kollidiert frontal mit einem stillstehenden Auto, das eine Masse von 800 kg hat. Beide Autos bleiben nach der Kollision miteinander verbunden stehen.
Berechne die Geschwindigkeit der Autos nach der Kollision.
Zunächst müssen wir den Impuls des Gesamtsystems vor der Kollision berechnen. Der Impuls eines Körpers wird berechnet, indem man die Masse des Körpers mit seiner Geschwindigkeit multipliziert.
Impuls vor der Kollision
Zahlenwerte eingesetzt:
(da das zweite Auto stillsteht)
Daraus ergibt sich:
Nach der Kollision sind die Autos miteinander verbunden und bewegen sich als ein System. Daher betrachten wir die Geschwindigkeit des Gesamtsystems nach der Kollision als die gleiche Geschwindigkeit für beide Autos.
Impuls nach der Kollision
| (vnach = Geschwindigkeit nach der Kollision)
Da die Autos nach der Kollision miteinander verbunden bleiben und die gleiche Geschwindigkeit haben, beträgt die Gesamtmasse die Summe der Massen beider Autos.
Daraus ergibt sich:
Da die resultierende Kraft auf das System Null ist, ist der Impuls vor der Kollision gleich dem Impuls nach der Kollision.
Gleichsetzen ergibt: Impuls vor der Kollision = Impuls nach der Kollision
Wir können als nächstes die gesuchte Endgeschwindigkeit berechnen, indem wir die obige Gleichung nach dieser auflösen:
Nach der Kollision haben die Autos eine Geschwindigkeit von 12 m/s.
In der nachfolgenden Lerneinheit schauen wir uns den Kraftstoß an.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team