PH3 – Gleichförmige Kreisbewegung [Definition, Kennzahlen, Beispiele]

Eine gleichförmige Kreisbewegung ist eine Bewegung, bei der sich ein Körper mit konstanter Winkelgeschwindigkeit um einen festen Punkt dreht. Das bedeutet, dass die Geschwindigkeit des Körpers entlang des Kreisumfangs konstant bleibt.

Da sich die Richtung des Körpers im Kreis ständig ändert, spricht man von einer beschleunigten Bewegung. Eine Beschleunigung ist nicht nur als Änderung der Geschwindigkeit, sondern ebenfalls als Änderung der Richtung definiert.

In einer gleichförmigen Kreisbewegung bleibt die Größe der Beschleunigung konstant, da die Geschwindigkeit konstant ist, sich aber die Richtung ständig ändert. Das führt zu einer Zentripetalbeschleunigung, die zum Kreismittelpunkt zeigt.

In dieser Lerneinheit betrachten wir die gleichförmige Kreisbewegung und zeigen dir, welche Formeln du hier benötigst und wie du diese anwendest. Die gleichförmige Kreisbewegung ist ein wichtiges Thema in der Physik.

Für ein optimales Verständnis helfen dir mehrere sehr ausführliche Beispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH3 – Einführung in die Kinematik.

Wir betrachten alle relevanten Kennzahlen für die gleichförmige Kreisbewegung. Du lernst dabei die folgenden Kennzahlen kennen:

Winkelmaße
Umfangsgeschwindigkeit
Drehzahl
Umlaufzeit
Frequenz
Winkelgeschwindigkeit sowie
Bahngeschwindigkeit
Zentripetalbeschleunigung

Gleichförmige Kreisbewegung – Definition

Eine gleichförmige Kreisbewegung ist eine Bewegung, bei welcher die Bahnkurve auf einem Kreis verläuft und der Betrag der Bahngeschwindigkeit konstant ist.

Eine gleichförmige Kreisbewegung ist dann gegeben, wenn sich ein Körper mit einer konstanten Geschwindigkeit auf einer kreisförmigen Bahn bewegt. Bei der gleichförmigen Kreisbewegung handelt es sich um eine beschleunigte Bewegung, weil sich die Richtung der Geschwindigkeit ständig ändert.

Kreisbewegungen

Kreisbewegungen spielen eine wichtige Rolle in unserem alltäglichen Leben. Die Drehung der Räder von Autos, die Drehung der Trommel in der Waschmaschine, viele Geräte im Haushalt (Mixer), aber auch innerhalb von Maschinen und Motoren treten Kreisbewegungen auf.

Gleichförmige Kreisbewegung – Beispiele im Alltag

Hier sind einige Beispiele:

Karussell: Ein Karussell auf einem Jahrmarkt dreht sich gleichmäßig im Kreis. Die Passagiere bewegen sich in einer gleichförmigen Kreisbewegung, da sie sich mit konstanter Geschwindigkeit um den Mittelpunkt des Karussells bewegen.
Ventilator: Die Rotorblätter eines Ventilators drehen sich in einer gleichförmigen Kreisbewegung, um Luft zu zirkulieren.
Waschmaschine: Beim Schleudern einer Waschmaschine rotieren die Kleidungsstücke in einer gleichförmigen Kreisbewegung, um das Wasser herauszuschleudern.
Elektrische Zahnbürste: Die Bürstenköpfe einer elektrischen Zahnbürste rotieren gleichförmig, um die Zähne zu reinigen.
Rundumleuchten: Bei Fahrzeugen wie Polizeiautos oder Baufahrzeugen drehen sich die Rundumleuchten in einer gleichförmigen Kreisbewegung, um auf sich aufmerksam zu machen.
Windmühle: Die Flügel einer Windmühle drehen sich gleichmäßig im Kreis, um Windenergie in mechanische Energie umzuwandeln.
Schallplattenspieler: Auf einem Schallplattenspieler bewegt sich der Tonarm in einer gleichförmigen Kreisbewegung über die Schallplatte, um den Klang zu erzeugen.

Das sind nur einige Beispiele für gleichförmige Kreisbewegungen im Alltag. Es gibt jedoch noch viele weitere Situationen, in denen dieses Konzept Anwendung findet.

Umfangsgeschwindigkeit

Die Umfangsgeschwindigkeit $v$ gibt Auskunft über die Geschwindigkeit, mit der sich ein Punkt gleichförmig auf einer Kreisbahn bewegt.

Umfangsgeschwindigkeit – Formel

$v = U \cdot n$

Die Umfangsgeschwindigkeit $v$ setzt sich zusammen aus dem Umfang $U$ des Kreises und der Drehzahl $n$ . Die Umfangsgeschwindigkeit hat die Einheit [m/s] und gibt an, wie viele Meter pro Sekunde ein Körper auf einer Kreisbahn zurücklegt.

Drehzahl

Die Drehzahl $n$ wird bestimmt zu:

Drehzahl – Formel

$n = \dfrac{u}{t}$

Die Einheit der Drehzahl ist [1/s]. Die Drehzahl $n$ gibt an, wie oft sich ein Körper in einer bestimmten Zeit um sich selbst dreht.

Beispiel: Drehzahl!

Ein Körper dreht sich 3 mal um sich selbst in 5s. Wie hoch ist die Drehzahl?

$n = \dfrac{u}{t} = \dfrac{3}{5s} = 0,6 \dfrac{1}{s}$

Umfang

Der Umfang $U$ eines Kreises kann über den Durchmesser $d$ und die Kreiszahl $\pi$ berechnet werden:

Umfang – Kreis – Formel

$U = d \cdot \pi$

Die Kreiszahl $\pi$ ist eine mathematische Konstante, welche das Verhältnis vom Umfang zum Durchmesser eines Kreises beschreibt. Hierbei handelt es sich um ein konstantes Verhältnis, welches sich mit der Größe des Kreises ändert:

$\pi = \dfrac{U}{d} = 3,14159…$

Je größer der Kreis, desto größer der Umfang und desto größer auch der Durchmesser. Umfang und Durchmesser erhöhen sich dabei um denselben Faktor, weshalb die Kreiszahl immer gleich groß ist. Auf dem Taschenrechner hat die Kreiszahl π ihre eigene Taste.

Setzen wir nun den Umfang $U = d \dcot \pi$ in die Umfangsgeschwindigkeit $v$ ein, so können wir diese auch berechnen zu:

Umfangsgeschwindigkeit – Formel

$v = d \cdot \pi \cdot n$

Umfangsgeschwindigkeit, Umfang, Drehzahl, Gleichförmige Kreisbewegung, Formeln — Umfangsgeschwindigkeit, Umfang, Drehzahl

Mit der obigen Gleichung zur Umfangsgeschwindigkeit $v$ , kann auch die Drehzahl $n$ berechnet werden, wenn wir diese nach $n$ auflösen:

Drehzahl berechnen – Formel

$n = \dfrac{v}{ d \cdot \pi}$

Umfangsgeschwindigkeit – Beispiele

Schauen wir uns mal einige Beispiele zur Umfangsgeschwindigkeit an.

Beispiel 1: Umfangsgeschwindigkeit berechnen

Aufgabenstellung

Die Riemenscheibe eines Bandschleifers hat den Durchmesser von 150mm und dreht sich pro Minute 1.620 mal.

Wie groß ist die Schleifbandgeschwindigkeit in Metern pro Sekunde?

Gegeben haben wir den Durchmesser $d = 150 mm$ und die Drehzahl $n = 1.620 \dfrac{1}{min}$ . Die Umfangsgeschwindigkeit $v$ ist hier gesucht und kann mit der folgenden Gleichung berechnet werden:

$v = d \cdot \pi \cdot n$

Wir müssen zunächst noch die Einheiten umrechnen. Dazu verwenden wir die SI-Einheiten Sekunde s und Meter m:

$d = 150 mm = 0,15 m$

$n = 1.620 \dfrac{1}{min} = 1.620 \dfrac{1}{60s} = 27 \dfrac{1}{s}$

Einsetzen der Werte:

$v = d \cdot \pi \cdot n = 0,15m \cdot \pi \cdot 27 \dfrac{1}{s} = 12,72 m/s$

Die Schleifbandgeschwindigkeit beträgt 12,72 Meter pro Sekunde.

Beispiel 2: Umfangsgeschwindigkeit

Aufgabenstellung

Eine Schleifscheibe zum Schleifen von Messern besitzt einen Radius von 50 mm. Die Scheibe ist für eine Umfangsgeschwindigkeit von 18 m/s zugelassen.

Wie schnell darf sich die Scheibe drehen?

Es ist der Radius $r = 50 mm$ gegeben. Der Durchmesser ist das Zweifache des Radius’:

$d = 2r = 100mm = 0,1m$

Außerdem ist die Umfangsgeschwindigkeit mit $v = 18 m/s$ gegeben.

Berechnet werden soll die Drehzahl $n$ .

Wir betrachten dazu die folgende Gleichung:

$v = d \cdot \pi \cdot n$

Gesucht ist die Drehzahl $n$ , wir lösen also die obigen Gleichung nach $n$ auf:

$n = \dfrac{v}{d \cdot \pi}$

Einsetzen der Werte:

$n = \dfrac{18 m/s}{0,1m \cdot \pi} = 57,3 \dfrac{1}{s}$

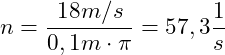
Die Scheibe darf sich 57,3 mal pro Sekunde drehen.

Umlaufzeit

Die Umlaufzeit $T$ ist die Zeit, die ein Punkt für eine volle Kreisumdrehung benötigt. Die Umlaufzeit ist umgekehrt proportional der Drehzahl $n$ . Sie wird in Sekunden angegeben:

Umlaufzeit – Formel

$T = \dfrac{1}{n}$

Die Einheit der Umlaufzeit wird in Sekunde [s] angegeben.

Frequenz

Die Frequenz $f$ ist der Quotient aus der Anzahl der vollen Umläufe $u$ und dem zugehörigen Zeitabschnitt $t$ . Betrachtet man nur einen Umlauf $u = 1$ , dann ist der Zeitabschnitt $t$ gleich der Umlaufzeit $T$ .

Frequenz – Formel

$f = \dfrac{u}{t}$

Die Frequenz ist der Kehrwert der Umlaufzeit $T$ :

$f = \dfrac{1}{T}$

Die Einheit der Frequenz ist das Hertz [ $\dfrac{1}{s} = Hz$ ].

Winkelgeschwindigkeit

Die Winkelgeschwindigkeit ω gibt an, wie schnell sich der Drehwinkel pro Zeiteinheit ändert. Sie wird oft in Einheiten wie Radiant pro Sekunde (rad/s) oder Grad pro Sekunde (°/s) gemessen. Wenn sich beispielsweise ein Objekt mit einer Winkelgeschwindigkeit von 20°/s dreht, bedeutet das, dass sich der Drehwinkel des Objekts um 20° pro Sekunde ändert.

Die Winkelgeschwindigkeit ω ist bei einer gleichförmigen Kreisbewegung der Quotient aus dem zurückgelegten Drehwinkel $\varphi$ [in Rad] und der dafür benötigten Zeit $t$ :

Winkelgeschwindigkeit – Formel

$\omega = \dfrac{\varphi}{t}$

Die Einheit der Winkelgeschwindigkeit ist Radiant pro Sekunde [rad/s].

Es ist nicht immer einfach den Winkel $\varphi$ genau anzugeben. Eine andere Möglichkeit ist es, die Winkelgeschwindigkeit $\omega$ über die volle Kreisumdrehung zu bestimmen. Eine volle Kreisumdrehung in Bogenmaß beträgt $\varphi = 2 \pi$ . Die Dauer für eine volle Kreisumdrehung ist die Umlaufzeit $t = T$ . Wir erhalten also für die Winkelgeschwindigkeit:

Winkelgeschwindigkeit – Formel 2

$\omega = \dfrac{2 \pi}{T}$

Wir können die Winkelgeschwindigkeit auch in Abhängigkeit von der Frequenz f darstellen:

Winkelgeschwindigkeit – Formel 3

$\omega = 2 \pi \cdot f$

Denn es gilt: $f = \dfrac{1}{T}$

Bahngeschwindigkeit

Die Bahngeschwindigkeit bei gleichförmiger Kreisbewegung ist nichts anderes als die Geschwindigkeit eines Punktes auf einer Kreisbahn, anstelle einer Strecke. Wir betrachten einen Körper, welcher sich gleichförmig auf einer Kreisbahn bewegt. Der Weg s, der vom Körper auf dem Kreis zurückgelegt wird, ist gleich der Bogenlänge b.

$b = \varphi \; [rad] \cdot r$

Wir gehen wieder von einer vollen Kreisbewegung aus und geben diese in Bogenmaß an, demnach gilt für den Winkel:

$\varphi = 2 \pi \; [rad]$

Wir setzen den obigen Winkel als nächstes in die Formel für die Bogenlänge ein und erhalten:

$b = 2 \pi \; [rad] \cdot r$

Der Weg s in Abhängigkeit von der Zeit wird allgemein wie folgt berechnet:

$s = v \cdot t$

Wir betrachten nun aber eine volle Kreisumdrehung, weshalb für die Zeit t die Umlaufzeit t = T eingesetzt werden muss:

$s = v \cdot T$

Da Weg s und Bogenlänge b auf einer Kreisbahn gleich sind, können wir die beiden Formeln gleichsetzen:

$2 \pi \; [rad] \cdot r = v \cdot T$

Auflösen nach der Bahngeschwindigkeit v:

$v = \dfrac{2 \pi \; [rad] \cdot r}{T}$

Und da:

$\omega = \dfrac{2 \pi}{T}$

Damit ergibt sich für die Bahngeschwindigkeit v:

Bahngeschwindigkeit

$v = \omega \cdot r$

Die Einheit der Bahngeschwindigkeit ist [m/s]. Die Bahngeschwindigkeit und die Umlaufgeschwindigkeit sind identisch. Zur Berechnung kannst du also auch die obigen Gleichungen für die Umlaufgeschwindigkeit verwenden (je nach gegebener Größe).

Betrachten wir eine konstante Winkelgeschwindigkeit, so gilt: Je größer der Abstand eines Punktes von der Drehachse ist, desto größer ist seine Bahngeschwindigkeit v.

Zentripetalbeschleunigung

Die Zentripetalbeschleunigung ist die Beschleunigung, die ein Körper erfährt, wenn es sich in einer Kreisbewegung befindet. Sie zeigt immer zum Mittelpunkt des Kreises und ist verantwortlich dafür, dass der Körper seine Richtung ändert und somit eine Kreisbahn beschreibt, obwohl seine Geschwindigkeit konstant ist.

Die Formel für die Zentripetalbeschleunigung über die Bahngeschwindigkeit v und den Radius r lautet:

Zentripetalbeschleunigung

$a_Z = \frac{v^2}{r}$

mit

$v$ Bahngeschwindigkeit [m/s]

$r$ Radius [m]

Wir können die Zentripetalbeschleunigung aber ebenfalls über die Winkelgeschwindigkeit ω bestimmen:

Zentripetalbeschleunigung

$a_Z = \omega^2 \cdot r$

mit

$\omega$ Winkelgeschwindigkeit in [rad/s]

$r$ Radius [m]

Gleichförmige Kreisbewegung: Zusammenfassung aller Formeln

$\varphi^\circ = \dfrac{180^\circ}{\pi} \cdot \varphi \; [rad]$	Radiant in Grad
$\varphi \; [rad] = \dfrac{\pi}{180^\circ} \cdot \varphi^\circ$	Grad in Radiant
$n = \dfrac{u}{t}$	Drehzahl n
$n = \dfrac{v}{ d \cdot \pi}$	Drehzahl n
$T = \dfrac{1}{n}$	Umlaufzeit T
$f = \dfrac{1}{T}$	Frequenz f
$\omega = \dfrac{2 \pi}{T}$	Winkelgeschwindigkeit ω
$\omega = 2 \pi \cdot f$	Winkelgeschwindigkeit ω
1 $v = \dfrac{2 \pi [rad] \cdot r}{T}$	Bahngeschwindigkeit/Umlaufgeschwindigkeit v
$v = \omega \cdot r$	Bahngeschwindigkeit/Umlaufgeschwindigkeit v
$v = U \cdot n$	Bahngeschwindigkeit/Umlaufgeschwindigkeit v
$v = d \cdot \pi \cdot n$	Bahngeschwindigkeit/Umlaufgeschwindigkeit v
$a_Z = \frac{v^2}{r}$	Zentripetalbeschleunigung
$a_Z = \omega^2 \cdot r$	Zentripetalbeschleunigung

Wir betrachten als nächstes zwei Beispiele für die gleichförmige Kreisbewegung.

Beispiel 1: Winkelgeschwindigkeit, Frequenz und Drehzahl

Aufgabenstellung

Gegeben sei ein Auto, welches mit einer Geschwindigkeit von 100 km/h über eine Landstraße fährt. Die Räder des Autos haben einen Durchmesser von 45 cm.

Berechne die Winkelgeschwindigkeit eines Rades sowie die Frequenz und die Drehzahl pro Minute!

In der Aufgabenstellung hast du die Geschwindigkeit von 100 km/h gegeben. Diese müssen wir noch in die SI-Einheit m/s umrechnen:

$100 km/h : 3,6 = 27,78 m/s$

Es ist außerdem der Durchmesser der Reifen mit $d = 45 cm$ gegeben. Auch hier rechnen wir in die SI-Einheit [m] um:

$45 cm : 100 = 0,45 m$

Winkelgeschwindigkeit

Wir sollen die Winkelgeschwindigkeit $\omega$ bestimmen. Hierfür benötigen wir die folgende Gleichung:

$v = \omega \cdot r$

Es kann nur diese Gleichung verwendet werden, denn es sind lediglich der Durchmesser (und damit Radius $r$ ) und die Geschwindigkeit $v$ gegeben. Wir müssen die Gleichung aber noch nach der Winkelgeschwindigkeit $\omega$ auflösen:

$\omega = \dfrac{v}{r}$

Der Radius ist die Hälfte des Durchmessers:

$r = \dfrac{d}{2} = \dfrac{0,45m}{2} = 0,225 m$

Als nächstes setzen wir die gegebenen Werte in die Gleichung der Winkelgeschwindigkeit $\omega$ ein:

$\omega = \dfrac{27,78 m/s}{0,225 m} = 123,47 \dfrac{1}{s}$

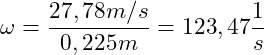
In einer Sekunde wird ein Winkel von 123,47 rad überstrichen. In Gradmaß ausgedrückt bedeutet das:

$\varphi^\circ = 123,4 \cdot \dfrac{180^\circ}{\pi} = 7074^\circ$

Es wird also pro Sekunde ein Winkel von 7074° überstrichen.

Das bedeutet für eine volle Kreisumdrehung mit 360°:

$\dfrac{7074^\circ}{360^\circ} = 19,65$

Die Drehung erfolgt pro Sekunde 19,65 mal. Dies entspricht der Drehzahl $n$ .

Drehzahl

Als nächstes können wir für die Berechnung der Drehzahl $n$ die folgende Gleichung verwenden:

$n = \dfrac{v}{ d \cdot \pi}$

Danach setzen wir die Werte ein:

$n = \dfrac{27,78 m/s}{0,45 m \cdot \pi} = 19,65 \dfrac{1}{s}$

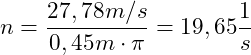
Pro Sekunde dreht sich der Reifen 19,65 um sich selbst.

In Minuten umgerechnet ergibt sich demnach:

$19,65 \dfrac{1}{s} = 19,65 \dfrac{1}{min} \cdot 60 = 1.179 \dfrac{1}{min}$ .

Pro Minute dreht sich der Reifen also 1.179 mal um sich selbst.

Frequenz

Als letztes fehlt uns noch die Frequenz. Diese berechnen wir aus der folgenden Gleichung:

$\omega = 2 \pi \cdot f$

Wir haben die Winkelgeschwindigkeit gegeben, somit können wir aus der obigen Gleichung die Frequenz bestimmen:

$f = \dfrac{\omega}{2 \pi}$

Danach setzen wir die bekannten Werte ein:

$f = \dfrac{123,47 \dfrac{1}{s} }{(2 \pi)} = 19,65 Hz$

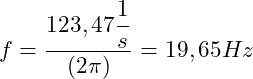
Die Frequenz bei einem Kreis ist gleich der Drehzahl!

Beispiel 2: Zentripetalbeschleunigung

Aufgabenstellung

Ein Fahrzeug bewegt sich in einer kreisbogenförmigen Kurve mit dem Radius 160 Metern. Die Zentripetalbeschleunigung darf aus Sicherheitsgründen höchstens 4,9 m/s² betragen.

Berechne die zulässige Höchstgeschwindigkeit des Fahrzeugs.

Wir können hier die Formel für die Zentripetalbeschleunigung heranziehen. Da wir die Geschwindigkeit v suchen, verwenden wir die folgende Gleichung:

$a_Z = \frac{v^2}{r}$

Wir haben die Zentripetalbeschleunigung und den Radius gegeben. Wir müssen die obige Formel nach der gesuchten Größe auflösen:

$v = \sqrt{a_z \cdot r}$

Wir setzen die gegebenen Werte ein:

$v = \sqrt{4,9 \frac{m}{s^2} \cdot 160 m} = 28 \frac{m}{s}$

Die zulässige Höchstgeschwindigkeit des Fahrzeugs in der Kurve beträgt 28 Meter pro Sekunde. Dies entspricht 100,8 km/h.

Wa gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++