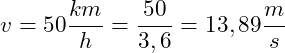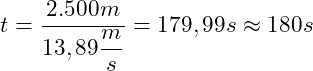PH3 – Gleichförmige Bewegung [Grundlagen, Beispiele, Videos, Aufgaben]

In dieser Lerneinheit betrachten wir die gleichförmige Bewegung von Körpern und zeigen dir, wie du Geschwindigkeit und zurückgelegten Weg berechnest.

Wir betrachten die gleichförmige Bewegung und zeigen die Formeln für die Berechnung von Geschwindigkeit und Weg auf.

Für ein optimales Verständnis helfen dir vier Videoclips und drei unterschiedliche Beispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH3 – Einführung in die Kinematik.

Von einer gleichförmigen Bewegung ist genau dann die Rede, wenn eine konstante Geschwindigkeit vorliegt und sich damit die Geschwindigkeit nicht ändert. Es tritt demnach keine Beschleunigung auf.

Gleichförmige Bewegung – Beispiele im Alltag

Im Alltag gibt es viele Beispiele für gleichförmige Bewegungen. Hier sind einige davon:

Das Pendeln eines Uhrzeigers: Der Sekundenzeiger einer Uhr bewegt sich in einer gleichförmigen Bewegung, da er sich mit konstanter Geschwindigkeit um das Zifferblatt bewegt.
Eine gleichmäßige Fahrt mit dem Fahrrad: Wenn du mit konstanter Geschwindigkeit auf einer geraden Straße ohne zu beschleunigen oder zu bremsen fährst, bewegst du dich gleichförmig.
Ein Auto auf einer langen, geraden Autobahn, das mit konstanter Geschwindigkeit fährt, zeigt eine gleichförmige Bewegung.
Ein Aufzug, der mit konstanter Geschwindigkeit zwischen den Stockwerken eines Gebäudes fährt, bewegt sich gleichförmig.
Ein Flugzeug im Reiseflug: Wenn ein Flugzeug seine Flughöhe hält und mit konstanter Geschwindigkeit geradeaus fliegt, kann man seine Bewegung als gleichförmig betrachten.
Einige Sportarten wie Langstreckenlauf oder Rudern können als Beispiele für gleichförmige Bewegungen dienen, wenn der Sportler eine konstante Geschwindigkeit beibehält.
Ein Rollschuhläufer, der auf einer geraden Strecke ohne zu beschleunigen oder zu bremsen fährt, führt eine gleichförmige Bewegung aus.

Diese Beispiele zeigen, wie die gleichförmige Bewegung in verschiedenen Alltagssituationen auftreten kann, wenn sich ein Objekt mit konstanter Geschwindigkeit entlang einer geraden Linie bewegt.

Wir wollen folgende Fragen beantworten:

Weg s – welchen Weg legt der Körper zurück?

Geschwindigkeit v – welche Geschwindigkeit weist der Körper auf?

Zeit t – wie lange benötigt der Körper mit der Geschwindigkeit v für den Weg x?

Es ist nun möglich eine der drei obigen Größen zu berechnen, wenn zwei Größen gegeben sind.

Gleichförmige Bewegung – Formeln

Für dich sind die folgenden Gleichungen bei einer gradlinigen gleichförmigen Bewegung wichtig:

Berechnung des Weges

Weg

$s = v \cdot t$

Mit dem Weg-Zeit-Gesetz kann der Weg $s$ berechnet werden, wenn Geschwindigkeit $v$ und Zeit $t$ gegeben sind. Die obige Gleichung kann nach der Geschwindigkeit $v$ aufgelöst werden:

Berechnung der Geschwindigkeit

Geschwindigkeit

$v = \dfrac{s}{t}$

Mit dem Geschwindigkeits-Zeit-Gesetz kann die Geschwindigkeit $v$ berechnet werden, wenn Weg $s$ und Zeit $t$ gegeben sind. Diese Gleichung kann nach der Zeit $t$ aufgelöst werden:

Berechnung der Zeit

Zeit

$t = \dfrac{s}{v}$

Mit dieser Gleichung kann die Zeit $t$ berechnet werden, wenn Weg $s$ und Geschwindigkeit $v$ gegeben sind.

SI-Einheiten

Bevor du mit den Berechnungen beginnen kannst, musst du die gegebenen Einheiten prüfen. Liegen diese nicht in SI-Einheiten vor, so musst du diese zunächst umrechnen. In der nachfolgenden Tabelle sind die SI-Einheiten von Geschwindigkeit, Weg und Zeit angegeben. Zudem findest du dort die Umrechnungen in die gängigen Einheiten.

	SI-Einheit	Umrechnung
Geschwindigkeit	Meter pro Sekunde [m/s]	$\cdot$ 3,6 = km/h
Weg	Meter [m]	: 1.000 = km
Zeit	Sekunde [s]	: 60 = min \| : 3.600 = h

Es ist sinnvoll die in der Aufgabenstellung gegebenen Einheiten zunächst in die SI-Einheiten umzurechnen, bevor du mit den Berechnungen beginnst.

Merk’s dir!

Die Geschwindigkeit wird selten in m/s, sondern in km/h angegeben. Die Umrechnung erfolgt über den Faktor 3,6:

Multiplizierst du m/s mit dem Faktor 3,6 so erhaltet ihr km/h.

Dividierst du km/h mit dem Faktor 3,6 so erhaltet ihr m/s.

In den folgenden vier Videos zeige ich dir, was die gleichförmige Bewegung ist, welche Gleichungen du für die Berechnung benötigst und wie du die Gleichungen anwendest.

Videoreihe – Gleichförmige Bewegung

Es folgen nun 4 Videoclips in denen wir dir zuerst die Definition und anschließend drei Beispiele ausführlich vorstellen.

Videoclip 1: Gleichförmige Bewegung -Definition

Videoclip 2: Gleichförmige Bewegung -Beispiel 1

Videoclip 3: Gleichförmige Bewegung -Beispiel 2

Videoclip 4: Gleichförmige Bewegung -Beispiel 3

Nachdem du dir die Videos angeschaut hast und die Gleichungen kennst, kannst du die folgenden Aufgaben lösen.

Beispiele zur gleichförmigen Bewegung

In den nachfolgenden Beispielen schauen wir Aufgaben zur gleichförmigen Bewegung an:

1. Beispiel: Berechnung des Weges
2. Beispiel: Berechnung der Zeit
3. Beispiel: Berechnung der Geschwindigkeit

Beispiel 1: Weg berechnen

Aufgabenstellung

Ein Fahrzeug bewegt sich mit einer Geschwindigkeit von 14 m/s.

Welchen Weg $s$ legt es in 2 Minuten zurück?

1. Schritt: Umrechnung der Einheiten in SI-Einheiten

Minuten müssen in Sekunden umgerechnet werden:

$t$ = 1 Minute = 60 Sekunden → 2 Minuten = 120 Sekunden

2. Schritt: Berechnung des Weges

$s = v \cdot t$

$s = 14 \dfrac{m}{s} \cdot 120s = 1.680 m = 1,68 km$

Beispiel 2: Zeit berechnen

Aufgabenstellung

Ein Fahrzeug bewegt sich mit einer Geschwindigkeit von 50 km/h. Es legt einen Weg von 2,5 km zurück.

Wie lange fährt das Fahrzeug für diesen Weg?

1. Schritt: Umrechnung der Einheiten in SI-Einheiten

$\dfrac{km}{h}$ muss in $\dfrac{m}{s}$ umgerechnet werden:

$v = 50 \dfrac{km}{h} = \dfrac{50}{3,6} = 13,89 \dfrac{m}{s}$

$km$ muss in $m$ umgerechnet werden:

$s = 2,5 km = 2.5 \cdot 1.000 m = 2.500 m$

2. Schritt: Berechnung der Zeit $t$

$t = \dfrac{s}{v}$

$t = \dfrac{2.500 m}{13,89 \dfrac{m}{s}} = 179,99s \approx 180s$

Beispiel 3: Geschwindigkeit berechnen

Aufgabenstellung

Ein Fahrzeug legt einen Weg von 3.000 m in einer Zeit von 50 Sekunden zurück. Es ist eine Höchstgeschwindigkeit von 130 km/h erlaubt.

Hält der Fahrer diese Geschwindigkeitsbegrenzung ein?

1. Schritt: Umrechnung der Einheiten in SI-Einheiten

Alle in SI-Einheiten angegeben.

2. Schritt: Berechnung der Geschwindigkeit

$v = \dfrac{s}{t}$

$v = \dfrac{3.000 m}{50 s} = 60 \dfrac{m}{s}$

3. Schritt: Umrechnung in km/h

$60 \dfrac{m}{s} = 60 \dfrac{3.600 km}{1.000 h} = 216 \dfrac{km}{h}$

Nein, der Fahrer hält sich nicht an die Geschwindigkeitsbegrenzung. Der Fahrer fährt 86 km/h schneller als erlaubt!

Was kommt als Nächstes?

Im nachfolgenden Kurstext betrachten wir das Weg-Zeit-Diagramm, wenn eine gleichförmige Bewegung gegeben ist.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++