PH3 – Schräger Wurf [Definition, Beispiele, Videos, Aufgaben]

Ein schräger Wurf (auch: schiefer Wurf) ist eine Bewegung eines Körpers, welcher sowohl horizontal als auch vertikal in einem Winkel zur Horizontalen geworfen wird. Diese Bewegung kann durch die Gravitationskraft beeinflusst werden. Der schräg abgeworfene Körper bewegt sich nicht nur horizontal oder vertikal, sondern in einer kombinierten Bewegung.

Die Bewegung eines schrägen Wurfs kann mithilfe der kinematischen Gleichungen der Bewegung analysiert werden, wobei sowohl die horizontale als auch die vertikale Komponente der Bewegung berücksichtigt werden. Die Schwerkraft wirkt während des gesamten Fluges und verändert die vertikale Geschwindigkeit des Objekts, während die horizontale Geschwindigkeit konstant bleibt, sofern keine Luftreibung oder andere Kräfte berücksichtigt werden müssen.

In dieser Lerneinheit betrachten wir den schrägen Wurf sowie die Formeln, welche du für Berechnungen zum schrägen Wurf benötigst.

Für ein optimales Verständnis helfen dir zwei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH3 – Einführung in die Kinematik.

Schräger Wurf | Schiefer Wurf – Definition

Schräger Wurf, schiefer Wurf, gleichförmige Bewegung, gleichmäßig beschleunigte Bewegung, Volleyball — Schräger Wurf – Volleyball

Beim schrägen Wurf erfolgt eine gleichförmige Bewegung (=konstante Geschwindigkeit) in horizontale Richtung (x-Richtung) und eine gleichmäßig beschleunigte Bewegung (=konstante Beschleunigung) in vertikale Richtung (y-Richtung). Die beiden Bewegungen die auftreten sind identisch zum waagerechten Wurf. Der Unterscheid zum waagerechten Wurf ist, dass der Körper nicht waagerecht, sondern schräg (mit Winkel) abgeworfen wird.

Schräger Wurf – Beispiele im Alltag

Hier sind einige Beispiele für den schrägen Wurf im Alltag:

Baseball: Wenn ein Baseballspieler den Ball schräg wirft, um ihn über die Entfernung hinweg zu einem anderen Spieler oder zum Schlagmann zu werfen, handelt es sich um einen schrägen Wurf. Der Ball fliegt in einer parabolischen Bahn und erreicht eine bestimmte Höhe, bevor er vom Feldspieler gefangen oder vom Schlagmann getroffen wird.
Fußball: Ein Spieler, der den Ball über das Spielfeld zu einem Mitspieler in der Ferne wirft, nutzt einen schrägen Wurf. Der Ball fliegt in einem Bogen durch die Luft, um die Distanz zu überbrücken und den gewünschten Spieler zu erreichen.
Wasserball: Beim Wasserball wird der Ball oft schräg geworfen, um ihn über die Köpfe der gegnerischen Spieler hinweg zu einem Teammitglied zu passen. Der Ball folgt einer gekrümmten Bahn und ermöglicht eine präzise Platzierung des Passes.
Frisbee: Beim Frisbee-Spielen erfolgt der Wurf normalerweise schräg, um die Flugweite und -richtung zu kontrollieren. Durch den schrägen Wurf kann der Spieler die gewünschte Flugkurve erzielen und den Frisbee gezielt zu einem anderen Spieler werfen.
Wasserrutsche: Wenn man eine Wasserrutsche hinunterrutscht, erfährt man einen schrägen Wurf. Der Körper wird entlang der gekrümmten Rutsche geworfen und folgt einer parabolischen Bahn, während man die Rutsche hinuntergleitet.
Bowling: Beim Bowling wird die Kugel schräg geworfen, um die Pins zu treffen. Der Spieler gibt der Kugel eine seitliche Rotation und zielt darauf ab, dass sie in einem Bogen in Richtung der Pins rollt.

Diese Beispiele verdeutlichen, wie der schräge Wurf in verschiedenen Sportarten und Alltagssituationen vorkommt. Die physikalischen Prinzipien, die dem schrägen Wurf zugrunde liegen, sind überall anwendbar, wo ein Objekt eine gekrümmte Flugbahn hat und eine bestimmte Distanz überbrücken soll.

Schräger Wurf – Ausnahmen / Einschränkungen

Hier sind einige Ausnahmen oder Einschränkungen des schrägen Wurfs:

Reibung und Luftwiderstand: Der schräge Wurf basiert auf der Annahme, dass keine Reibungskräfte oder Luftwiderstand vorhanden sind. In der realen Welt wirken jedoch immer solche Kräfte auf Objekte, die durch die Luft fliegen. Insbesondere bei sehr schnellen oder langen Würfen können diese Faktoren die Flugbahn beeinflussen und zu Abweichungen führen.
Komplexe Umgebungen: Der schräge Wurf berücksichtigt keine komplexen Umgebungen oder Hindernisse, die die Flugbahn eines geworfenen Objekts beeinflussen können. In der Praxis können Bäume, Gebäude, Wind oder andere Hindernisse die Flugbahn verändern und die erwarteten Ergebnisse eines schrägen Wurfs beeinflussen.
Elastische Kollisionen: Der schräge Wurf basiert auf der Annahme, dass keine Kollisionen mit anderen Objekten während des Flugs stattfinden. In einigen Fällen können jedoch elastische Kollisionen auftreten, bei denen das geworfene Objekt mit einem anderen Objekt zusammenstößt und seine Bahn beeinflusst.

Es ist wichtig zu beachten, dass der schräge Wurf ein ideales Modell darstellt, um die Flugbahn eines Objekts zu analysieren, wenn bestimmte Bedingungen erfüllt sind. In der Realität können jedoch verschiedene Faktoren die Flugbahn beeinflussen und zu Abweichungen von den theoretischen Vorhersagen führen.

Schräger Wurf: Geschwindigkeiten zerlegen

Die Anfangsgeschwindigkeit v₀ muss beim schrägen Wurf in eine Geschwindigkeit $v_{0x}$ in x-Richtung und eine Geschwindigkeit $v_{0y}$ in y-Richtung zerlegt werden. Die Zerlegung der Geschwindigkeit erfolgt über das bereits bekannte Vorgehen der Zerlegung von Kräften.

Zerlegung in x-Richtung (horizontal):

$v_{0x} = v_0 \cdot \cos(\alpha)$

Zerlegung in y-Richtung (vertikal)

$v_{0y} = v_0 \cdot \sin(\alpha)$

Die Bewegung in x-Richtung erfolgt durch den waagerechten Anteil des Abwurfs. Die Bewegung in y-Richtung erfolgt einmal durch den vertikalen Anteil des Abwurfs in die Höhe sowie durch die Erdanziehung des Körpers mit der Fallbeschleunigung $g = 9,81 \frac{m}{s^2}$ . Die Wurfbahn beim schrägen Wurf beschreibt eine Parabel.

Schräger Wurf, schiefer Wurf, Parabel, Aufwärtsbewegung, Abwärtsbewegung, Geschwindigkeit, Weg, Höhe — Schräger Wurf: Parabel

Betrachten wir den schrägen Wurf mal etwas genauer:

Die erste Bewegung ist die Abwurfbewegung in x- und y-Richtung, es erfolgt also ein schräger Wurf. Hier muss die Anfangsgeschwindigkeit v₀ (auch: Abwurfgeschwindigkeit) in eine x- und eine y-Komponente zerlegt werden.
Die Bewegung in x-Richtung erfolgt über den gesamten Wurf mit konstanter Geschwindigkeit (=gleichförmige Bewegung). Die Bewegung in y-Richtung entspricht dem senkrechten Wurf nach oben und setzt sich aus der Abwurfgeschwindigkeit in y-Richtung sowie der Fallbeschleunigung g zusammen.
Die Abwurfgeschwindigkeit v₀ und die Aufprallgeschwindigkeit sind identisch, wenn die Höhe des Abwurfs mit der Höhe des Aufpralls überein stimmt.
Die gesamte Flugdauer entspricht der zweifachen Steigzeit ( 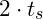$2 \cdot t_s$ ), da Steigzeit und Fallzeit identisch sind, wenn Abwurf- und Aufprallgeschwindigkeit übereinstimmen.

Schräger Wurf Formeln

Für die Bewegung in x-Richtung verwenden wir die Gleichungen der gleichförmigen Bewegung und für die Bewegung in y-Richtung die Gleichungen für den senkrechten Wurf nach oben. Wir ersetzen dabei die Geschwindigkeiten durch die oben berechneten Geschwindigkeitskomponenten und erhalten dann die Gleichungen für den schrägen Wurf:

Bewegung in x-Richtung (gleichförmige Bewegung):
$s_x = v_0 \cdot \cos(\alpha) \cdot t$	Wurfweite in Abhängigkeit von der Zeit
$s_x = v_0 \cdot \cos(\alpha) \cdot T$	Gesamte Wurfweite
Bewegung in y-Richtung (senkrechter Wurf nach oben)
$s_y = v_0 \cdot \sin(\alpha) \cdot t - \dfrac{1}{2} \cdot g \cdot t^2$	Wurfhöhe in Abhängigkeit von der Zeit
$h_{max} = v_0 \cdot \sin(\alpha) \cdot t_s - \dfrac{1}{2} \cdot g \cdot t_s^2$	max. Höhe /Scheitelhöhe in Abhängigkeit von der Zeit
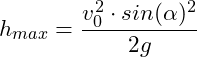$h_{max} = \dfrac{v_0^2 \cdot sin(\alpha)^2 }{2g}$	max. Höhe/ Scheitelhöhe
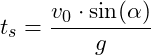$t_s = \dfrac{v_0 \cdot \sin(\alpha)}{g}$	Steigzeit
$T = 2 \cdot t_s$	Wurfzeit
Geschwindigkeiten
$v_{0x} = v_0 \cdot \cos(\alpha)$	Geschwindigkeit in x-Richtung
$v_{0y} = v_0 \cdot \sin(\alpha) - g \cdot t$	Geschwindigkeit in y-Richtung
$v = \sqrt{v_{0x}^2 + v_{0y}^2}$	Resultierende Geschwindigkeit

Video – Schiefer Wurf

In den nachfolgenden Videos zeige ich dir nochmals auf, welche Gleichungen du benötigst und wie du die Berechnungen durchführst.

Schräger Wurf Beispiel

Aufgabenstellung

Ein Ball wird mit 15 m/s unter einem Winkel von 29 Grad (schräg) geworfen.

a) Wie hoch ist der Ball an seinem höchsten Punkt?

b) Nach welcher Zeit erreicht er den höchsten Punkt?

c) Wie weit fliegt der Ball insgesamt?

d) Wie lange fliegt der Ball insgesamt?

e) Mit welcher Geschwindigkeit trifft der Ball auf dem Boden auf?

Lösung a) Gesamthöhe

Wir haben die Anfangsgeschwindigkeit $v_0 = 15 \frac{m}{s}$ gegeben, den Winkel $\alpha = 29^\circ$ und die Fallbeschleunigung mit $g = 9,81 \frac{m}{s}$ .

Wie hoch fliegt der Ball insgesamt?

Der höchste Punkt ist bei einer Parabel der Scheitelpunkt. Wir benötigen also für die Berechnung die folgende Gleichung:

$h_{max} = \frac{v_0^2 (\sin(\alpha))^2}{2 \cdot g}$

Wo kommt die Gleichung her?

Diese Gleichung ergibt sich, wenn wir den Weg des Balls ins y-Richtung (in die Höhe) betrachten:

$s_y = v_0 \cdot \sin(\alpha) \cdot t - \dfrac{1}{2} \cdot g \cdot t^2$

Wenn wir nun in diese Gleichung die maximale Steigzeit $t_s$ einsetzen, also die Zeit, die der Ball aufsteigt, dann erhalten wir die maximale Steighöhe:

$s_y = h_{max} = v_0 \cdot \sin(\alpha) \cdot t_s - \dfrac{1}{2} \cdot g \cdot t_s^2$

mit

$t_s = \dfrac{v_0 \cdot \sin(\alpha)}{g}$

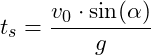
ergibt sich dann:

$h_{max} = v_0 \cdot \sin(\alpha) \cdot (\dfrac{v_0 \cdot \sin(\alpha)}{g})- \dfrac{1}{2} \cdot g \cdot (\dfrac{v_0 \cdot \sin(\alpha)}{g})^2$

$h_{max} = \dfrac{v_0^2 \cdot \sin(\alpha)^2}{g} - \dfrac{1}{2} \cdot g \cdot \dfrac{v_0^2 \cdot \sin(\alpha)^2}{g^2}$

$h_{max} = \dfrac{v_0^2 \cdot \sin(\alpha)^2}{g} - \dfrac{1}{2} \cdot \dfrac{v_0^2 \cdot \sin(\alpha)^2}{g}$

$h_{max} = \dfrac{1}{2} \cdot \dfrac{v_0^2 \cdot \sin(\alpha)^2}{g}$

$h_{max} = \dfrac{v_0^2 \cdot \sin(\alpha)^2}{2g}$

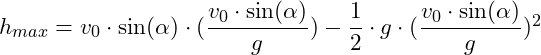
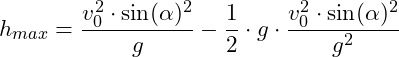
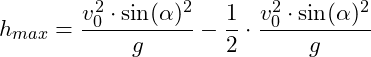
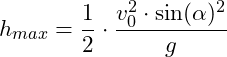
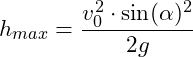
Einsetzen der Werte:

$h_{max} = \frac{(15 \frac{m}{s})^2 (\sin(29^\circ))^2}{2 \cdot 9,81 \frac{m}{s^2}} = 2,7 m$

Der Ball erreicht eine Höhe von 2,7m.

Lösung b) Steigzeit

Nach welcher Zeit erreicht er den höchsten Punkt?

Der höchste Punkt ist die Scheitelhöhe der Parabel. Bevor der Ball die Scheitelhöhe erreicht, steigt er nach oben (Aufwärtsbewegung). Wir wollen also die Steigzeit $t_s$ bestimmen:

$t_s = \frac{v_0 \cdot \sin(\alpha)}{g}$

Einsetzen der Werte:

$t_s = \frac{15 \frac{m}{s} \cdot \sin(29^\circ)}{9,81 \frac{m}{s^2}} = 0,74s$

Der Ball benötigt bis zur Erreichung der Scheitelhöhe 0,74 Sekunden.

Lösung c) Wurfweite / Flugweite

Wie weit fliegt der Ball?

Wir wollen wissen, welchen Weg der Ball in x-Richtung zurücklegt (=Wurfweite). Dazu verwenden wir die folgende Gleichung:

$s_x = v_0 \cos(\alpha) \cdot 2 \cdot t_s$

Einsetzen der Werte:

$s_x = 15 \frac{m}{s} \cos(29^\circ) \cdot 2 \cdot t_s$

Wir benötigen zur Berechnung der Wurfweite noch die Steigzeit $t_s$ , die wir in Aufgabenteil b) berechnet haben:

$t_s = 0,74s$

Einsetzen:

$s_x = 15 \frac{m}{s} \cos(29^\circ) \cdot 2 \cdot 0,74s = 19,42m$

Der Ball legt einen Weg von 19,42 m zurück.

Lösung d) Steighöhe + Fallzeit

Wie lange fliegt der Ball insgesamt?

Steighöhe $t_s$ und Fallzeit $t_F$ sind in diesem Fall gleich, da der Ball vom Boden aus abgeworfen wird und demnach genauso hoch fliegt (bis zum Scheitelpunkt), wie er fällt (nach dem Scheitelpunkt). Demnach kannst du ganz einfach die Steigzeit $t_s$ mal zwei nehmen:

$T = 2 \cdot t_s = 2 \cdot 0,74s = 1,48s$

Der Ball fliegt insgesamt 1,48s.

Lösung e) Aufprallgeschwindigkeit

Wir wollen noch wissen, mit welcher Geschwindigkeit der Ball auf dem Boden aufkommt. Dazu müssen wir zunächst die beiden Geschwindigkeit beim Aufprall nach der Zeit $T = 1,48s$ berechnen.

Wir starten mit der Geschwindigkeit in $x$ -Richtung:

$v_x = v_0 \cdot \cos(\alpha)$

Diese ist konstant und damit zeitunabhängig:

$v_x = 15 \frac{m}{s}\cdot \cos(29^\circ) = 13,12 \frac{m}{s}$

Danach berechnen wir die Geschwindigkeit in y-Richtung:

$v _y = v_{0} \cdot sin(\alpha) - g \cdot t$

Diese ist gleichmäßig beschleunigt, also zeitabhängig mit $t = T = 1,48s$ :

$v _y = 15 \frac{m}{s} \cdot sin(\alpha) - 9,81 \frac{m}{s^2} \cdot 1,48s = -7,25 \frac{m}{s}$

Das Minuszeichen resultiert, weil der Ball zunächst mit 15 m/s nach oben geworfen wird, dann aber nach unten fällt. Das Minuszeichen gibt also die entgegengesetzte Richtung zum Wurf (nach oben) an, die infolge der Erdanziehung resultiert.

Einsetzen in die folgende Gleichung:

$v = \sqrt{v_x^2 + v_y^2} = \sqrt{(13,12 \frac{m}{s})^2 + (-7,25 \frac{m}{s})^2}$

Nicht vergessen, dass das Minuszeichen mit quadriert wird und der Wert damit positiv wird:

$v = 14,98 \frac{m}{s} \approx 15 \frac{m}{s}$

Die Aufprallgeschwindigkeit beträgt 15 m/s.

Schräger Wurf Beispiel, Schräger Wurf Formeln, Schräger Wurf, Schiefer Wurf — Ergebnisse: Schräger Wurf Beispiel

Da die Abwurfhöhe und die Aufprallhöhe identisch sind, sind die Abwurfgeschwindigkeit und die Aufprallgeschwindigkeit ebenfalls identisch.

Was kommt als Nächstes?

Nachdem du nun das Thema Schräger Wurf kennst, betrachten wir in der folgenden Lerneinheit die gleichförmige Kreisbewegung.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++