[PH3] Senkrechter Wurf nach unten | Grundlagen, Beispiele, Aufgaben

In dieser Lerneinheit behandeln wir das Thema: Senkrechter Wurf nach unten. Diese Thema taucht immer wieder in der Physik auf und ist für deine Prüfung relevant.

In dieser Lerneinheit behandeln wir das Thema: Senkrechter Wurf nach unten. Diese Thema taucht immer wieder in der Physik auf und ist für deine Prüfung relevant.

Für ein optimales Verständnis helfen dir zwei unterschiedliche Beispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH3 – Einführung in die Kinematik.

Was der senkrechte Wurf nach unten??

Definition

Was ist der senkrechte Wurf nach unten?

Der senkrechte Wurf nach unten beschreibt die Bewegung eines Körpers, der mit einer Anfangsgeschwindigkeit $v_0$ in vertikaler Richtung (nach unten) geworfen wird. Die Besonderheit im Vergleich zum freien Fall liegt in der Abwurfgeschwindigkeit: Beim freien Fall wird der Körper lediglich losgelassen, sodass einzig die Fallbeschleunigung $g$ wirkt. Beim senkrechten Wurf nach unten wird der Körper jedoch mit einer bestimmten Geschwindigkeit abgeworfen, wodurch zwei Faktoren wirken:

Die Abwurfgeschwindigkeit $v_0$ .
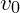Die konstante Erdbeschleunigung 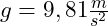$g = 9,81 \frac{m}{s^2}$ (unter Vernachlässigung des Luftwiderstands).

Du hast sicherlich schon mal einen Stein oder eine Münze in einen Brunnen geworfen. Dieser Vorgang ist ein senkrechter Wurf nach unten. Wenn du diesen Kurstext durchgearbeitet hast, dann kannst du

die Dauer berechnen, die der Stein benötigt, um am Brunnenboden anzukommen,
die Geschwindigkeit, mit welcher der Stein aufkommt und
den Weg, welchen der Stein zurücklegt, also die Tiefe des Brunnens.

Merk’s dir!

Bei einem senkrechten Wurf nach unten gelten die Gleichungen wie beim freien Fall, nur dass zusätzlich eine Abwurfgeschwindigkeit v₀ berücksichtigt werden muss.

Senkrechter Wurf nach unten – Beispiele im Alltag

Hier sind einige Beispiele für den senkrechten Wurf nach unten im Alltag:

Fallenlassen eines Gegenstands: Wenn du zum Beispiel einen Stift fallen lässt, fällt er senkrecht nach unten. Die einzige Kraft, die auf den Stift wirkt, ist die Schwerkraft, und er beschleunigt mit 9,8 m/s² in Richtung Boden.
Fallenlassen von Wasser aus einem Behälter: Wenn du Wasser aus einem Behälter gießt, fällt das Wasser senkrecht nach unten. Es folgt einer parabolischen Bahn, da es gleichzeitig nach unten beschleunigt wird.
Herunterfallende Blätter: Wenn Blätter von einem Baum fallen, folgen sie einem senkrechten Wurf nach unten. Die Schwerkraft zieht sie in Richtung Boden, und sie beschleunigen entsprechend.
Ein Ball, der zu Boden fällt: Wenn du einen Ball in die Luft wirfst und er dann fällt, folgt er einem senkrechten Wurf nach unten. Sobald er den höchsten Punkt seiner Bahn erreicht hat, beschleunigt er aufgrund der Schwerkraft in Richtung Boden.

Diese Beispiele zeigen, dass der senkrechte Wurf nach unten im Alltag häufig vorkommt, wenn Gegenstände fallengelassen oder geworfen werden und nur die Schwerkraft auf sie wirkt.

Senkrechter Wurf nach unten – Formeln

Die folgenden Gleichungen sind relevant, wenn ein senkrechter Wurf nach unten vorliegt:

$v = v_0 + g \cdot t$	Geschwindigkeit
$s = v_0 \cdot t + \dfrac{1}{2} \cdot g \cdot t^2$	zurückgelegter Weg
$h = H - s$	Höhe
$v = \sqrt{v_0^2 + 2 \cdot g \cdot s}$	Geschwindigkeit
$t_F = \dfrac{v - v_0}{g}$	Fallzeit
$H = s_{max} = v_0 \cdot t_F + \dfrac{1}{2} \cdot g \cdot t_F^2$	Gesamthöhe / maximal zurückgelegter Weg

Diagramme: Senkrechter Wurf nach unten

Beschleunigungs-Zeit-Diagramm (a-t-Diagramm): Die Beschleunigung ist konstant bei 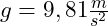$g = 9,81 \frac{m}{s^2}$ . Das Diagramm zeigt daher eine waagerechte Gerade parallel zur Zeitachse.
Geschwindigkeits-Zeit-Diagramm (v-t-Diagramm): Die Geschwindigkeit steigt linear an, da der Körper gleichmäßig beschleunigt wird. Die Gerade startet jedoch bei der Anfangsgeschwindigkeit $v_0$ .
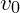Weg-Zeit-Diagramm (s-t-Diagramm): Der zurückgelegte Weg zeigt einen parabelförmigen Verlauf, da die Geschwindigkeit quadratisch mit der Zeit zunimmt.

Diagramme: Senkrechter Wurf nach unten

Schauen wir uns mal an wie die Diagramme ausschauen, wenn ein senkrechter Wurf nach unten gegeben ist:

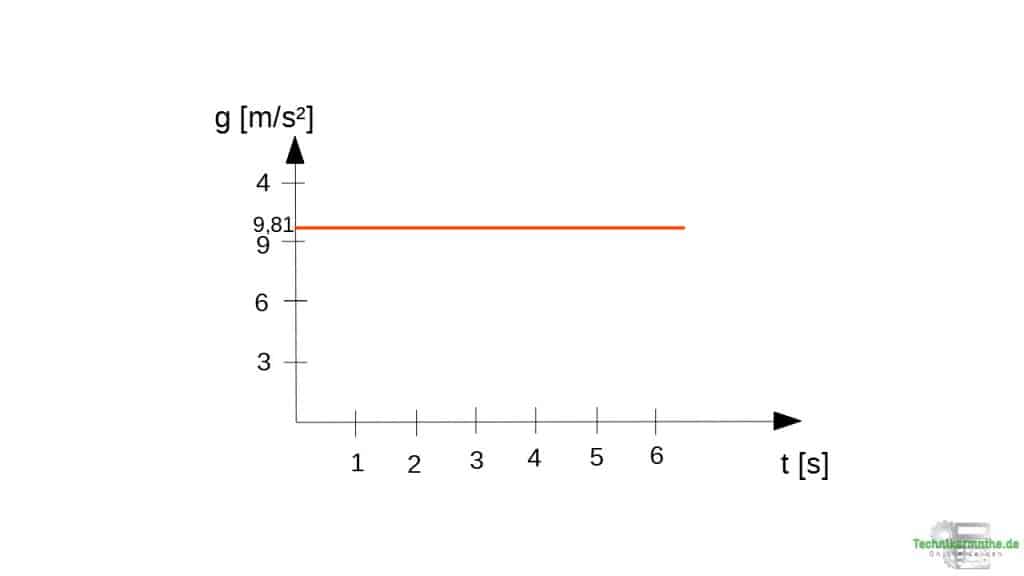
Senkrechter Wurf nach unten, a-t Diagramm, Beschleunigung, Zeit, senkrechter Wurf, Fallbeschleunigung — Senkrechter Wurf nach unten: a-t-Diagramm

Im Beschleunigungs-Zeit-Diagramm (a-t-Diagramm) ergibt sich eine konstante Fallbeschleunigung von 9,81 m/s². Damit haben wir eine Gerade gegeben, die parallel zur Zeitachse verläuft, weil sich die Fallbeschleunigung mit der Zeit nicht ändert.

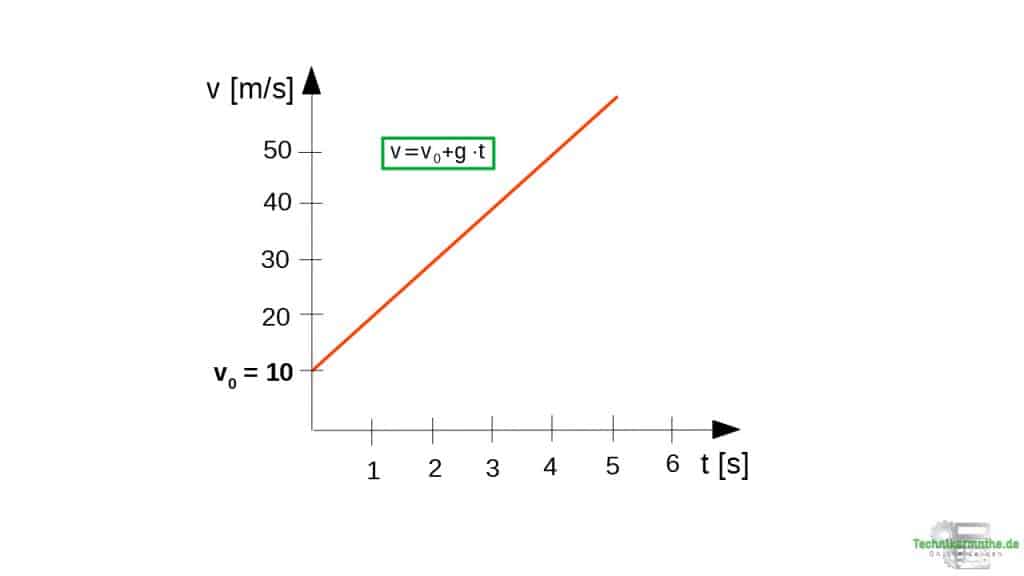
Senkrechter Wurf nach unten, v-t Diagramm, Geschwindigkeit — Senkrechter Wurf nach unten: v-t-Diagramm

Im Geschwindigkeits-Zeit-Diagramm ergibt sich eine lineare Geschwindigkeitsfunktion. Die Geschwindigkeit nimmt also linear mit der Zeit zu. Die Steigung ist konstant, d.h. pro Zeiteinheit erfährt der fallende Körper immer die gleiche Geschwindigkeitssteigerung. Der Unterschied zum freien Fall ist, dass die Anfangsgeschwindigkeit v₀ durch den Abwurf noch berücksichtigt werden muss. Die Funktion startet also nicht im Koordinatenursprung.

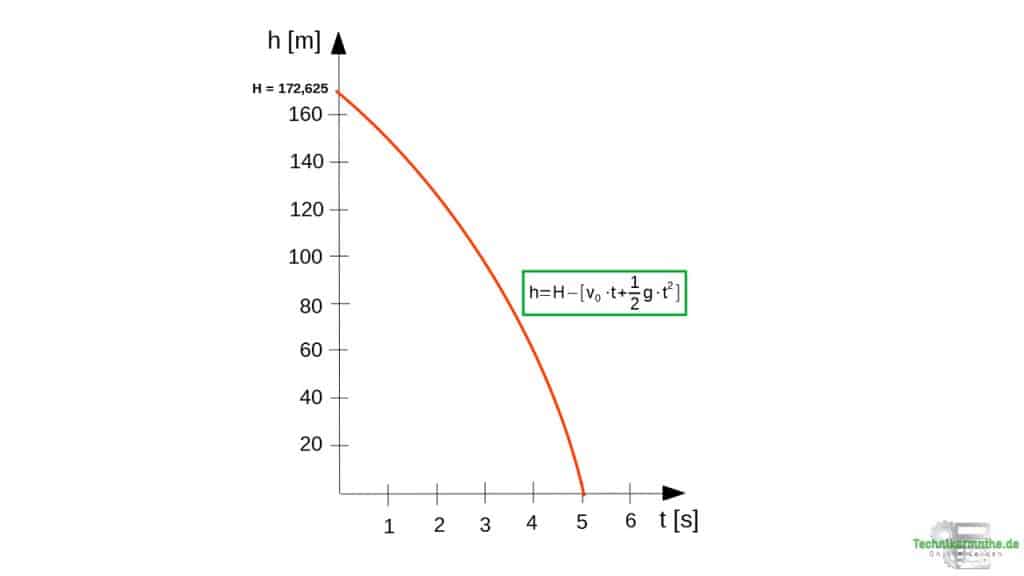
Senkrechter Wurf nach unten, s-t Diagramm, Höhe, Weg, Abwurfgeschwindigkeit, Weg-Zeit-Funktion, Weg-Zeit-Gesetz — Senkrechter Wurf nach unten: s-t Diagramm

Wir betrachten beim senkrechten Wurf nach unten die Höhe h auf der y-Achse. Der Körper wird also aus einer Gesamthöhe H abgeworfen. Die Höhe h ist dabei die Höhe, in welcher sich der Körper zu einer bestimmten Zeit befindet. Es ergibt sich ein parabelförmiger Weg-Zeit-Verlauf.

In den obigen Diagrammen wird eine Abwurfgeschwindigkeit von $v_0 = 10 m/s$ angenommen und die Dauer des Falls von 5 Sekunden. Die Höhe aus welcher der Körper fällt beträgt demnach:

$s_{max} = H = v_0 \cdot t_F+ \dfrac{1}{2} \cdot g \cdot t_F^2$

Einsetzen der Werte:

$H = 10 \dfrac{m}{s} \cdot 5s + \dfrac{1}{2} \cdot 9,81 \dfrac{m}{s^2} \cdot (5s)^2 = 172,625m$

Als nächstes betrachten wir zwei Beispiele zum Thema: Senkrechter Wurf nach unten. Versuche die Aufgaben zunächst selbstständig zu lösen, bevor du dir die Lösungen anschaust.

Beispiel 1: Aufprallgeschwindigkeit und Tiefe berechnen

Aufgabenstellung

Ein Stein wird mit einer Anfangsgeschwindigkeit von $v_0 = 7 m/s$ senkrecht nach unten in einen Schacht geworfen. Nach $t = 2s$ wird ein Aufprall festgestellt. Schall und Luftwiderstand sollen vernachlässigt werden.

Berechne die Aufprallgeschwindigkeit! Wie tief ist der Schacht?

Gegeben ist die Fallbeschleunigung von $g = 9,81 \dfrac{m}{s^2}$ , die Fallzeit $t_F = 2s$ und die Abwurfgeschwindigkeit $v _0 = 7 \dfrac{m}{s}$ .

Berechnet werden sollen die Aufprallgeschwindigkeit $v_{max}$ und die Tiefe des Schachts $H$ . Die Tiefe können wir über den insgesamt zurückgelegten Weg $s_{max}$ berechnen. Dazu verwenden wir die folgenden Gleichungen:

$v = v_0 + g \cdot t$

$s_{max} = v_0 \cdot t_F+ \dfrac{1}{2} \cdot g \cdot t_F^2$

Wir starten mit der Aufprallgeschwindigkeit (=maximale Geschwindigkeit). Diese können wir aus der 1. Gleichung berechnen, indem wir die Fallzeit $t_F = 2s$ für $t$ einsetzen:

$v_{max} = 7 \dfrac{m}{s} + 9,81 \dfrac{m}{s^2} \cdot 2s = 26,62 \dfrac{m}{s}$

Die Tiefe des Schachtes können wir über die gesamte zurückgelegte Wegstrecke bestimmen. Welchen Weg legt der Stein insgesamt zurück? Um das herauszufinden, setzen wir die Fallzeit $t_F = 2s$ in die zweite Gleichung ein:

$s_{max} = 7 \dfrac{m}{s} \cdot 2s + \dfrac{1}{2} \cdot 9,81 \dfrac{m}{s^2} \cdot (2s)^2 = 33,62 m$

Der Stein legt in der Fallzeit von 2 Sekunden eine Strecke von 33,62 m zurück. Demnach weist der Schacht eine Tiefe von 33,62 m auf.

Merk’s dir!

Wir vernachlässigen bei der Berechnung den Schall. Prallt der Stein auf dem Brunnenboden auf, hören wir den Aufprall zeitversetzt, da der Schall auch einen Weg zurück legen muss. Die Schallgeschwindigkeit in trockener Luft von 20 °C beträgt 343,2 m/s (1236 km/h).

Beispiel 2: Aufprallgeschwindigkeit berechnen

Aufgabenstellung

Dein bester Kumpel steht bei dir unten im Garten und ruft dich auf den Balkon. Er hat seinen Akkubohrer bei dir liegen gelassen. Da er keine Lust hat wieder bis zum 3. Stock zu dir hochzulaufen, bittet er dich, den Akkubohrer herunterzuwerfen.

Wie groß wird die Geschwindigkeit sein, mit welcher dein Freund den Akkubohrerkoffer in einer Höhe von 2m auffängt, wenn du den Bohrer mit einer Anfangsgeschwindigkeit von 5 m/s aus einer Höhe von 10,5 m abwirfst?

Gegeben:

Anfangsgeschwindigkeit: $v_0 = 5 m/s$

Abwurfhöhe: $H = 10,5 m$

Auffanghöhe: $h = 2m$

Zurückgelegter Weg: $s = 10,5m - 2m = 8,5 m$

Gesucht:

$v$ Aufprallgeschwindigkeit

Wir benötigen die Gleichung für die Geschwindigkeit:

$v = \sqrt{v_0^2 + 2 \cdot g \cdot s}$

Einsetzen der gegebenen Werte:

$v = \sqrt{(5 \dfrac{m}{s})^2 + 2 \cdot 9,81 \dfrac{m}{s^2} \cdot 8,5m} = 13,85 \dfrac{m}{s}$

Der Akkubohrerkoffer erreicht deinen Freund mit einer Geschwindigkeit von 13,85 Metern pro Sekunde. Dies entspricht $13,85 \cdot 3,6 = 49,86 km/h$ .

Autsch! Vielleicht beim nächsten Mal doch lieber nach unten tragen?

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist der Unterschied zwischen freiem Fall und senkrechtem Wurf?

Beim senkrechten Wurf nach unten gibt es eine Anfangsgeschwindigkeit $v_0$ , während der freie Fall ohne Abwurfgeschwindigkeit beginnt.

2. Welche Faktoren beeinflussen den senkrechten Wurf nach unten?

Die Anfangsgeschwindigkeit $v_0$ , die Fallbeschleunigung $g$ und die Fallzeit $t$ .

3. Wie berechnet man die Aufprallgeschwindigkeit?

Die Geschwindigkeit ergibt sich aus $v = \sqrt{v_0^2 + 2 \cdot g \cdot s}$ .

4. Welche Form hat das s-t-Diagramm?

Das Weg-Zeit-Diagramm zeigt eine Parabel, da der Weg quadratisch von der Zeit abhängt.

5. Warum ist der Luftwiderstand nicht berücksichtigt?

Zur Vereinfachung der Berechnung vernachlässigt man den Luftwiderstand. Real würde er die Geschwindigkeit verringern.

Zusammenfassung

Der senkrechte Wurf nach unten beschreibt die vertikale Bewegung eines Körpers, der mit einer Anfangsgeschwindigkeit $v_0$ nach unten geworfen wird. Die Bewegung ist gekennzeichnet durch die konstante Fallbeschleunigung $g = 9,81 \frac{m}{s^2}$ . Wichtige Gleichungen helfen bei der Bestimmung von Geschwindigkeit, Fallzeit und zurückgelegtem Weg. Diagramme verdeutlichen den linearen Anstieg der Geschwindigkeit und die parabelförmige Bahn des Weges.

Was kommt als Nächstes?

Nachdem wir dich jetzt mit dem Thema senkrechter Wurf nach unten vertraut gemacht haben und du jetzt alle relevanten Berechnungen zu diesem Thema kennst, wollen wir dir in der folgenden Lerneinheit die zusammengesetzte Bewegung erklären.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++