Geschwindigkeit-Zeit-Diagramm – Definition
Das Geschwindigkeits-Zeit-Diagramm oder auch v-t-Diagramm zeigt die Geschwindigkeit eines Körpers in Abhängigkeit von der Zeit an. Je nachdem welche Bewegung gegeben ist, verläuft die Geschwindigkeits-Zeit-Funktion konstant (bei gleichförmiger Bewegung) oder linear (bei gleichmäßig beschleunigter Bewegung).

Die Geschwindigkeits-Zeit-Funktion bei einer gleichmäßig beschleunigten Bewegung (=konstante Beschleunigung) ist linear, d.h. sie nimmt linear mit der Zeit t zu und weist damit eine konstante Steigung auf.

Das Geschwindigkeits-Zeit-Diagramm (auch: v-t-Diagramm) zeigt an, wie groß die Geschwindigkeit v nach einer bestimmten Zeit t ist. Bei der gleichmäßig beschleunigten Bewegung ergibt sich eine lineare Funktion, d.h. die Geschwindigkeit nimmt mit der Zeit t linear zu. Die Zeit t mit der SI-Einheit Sekunden [s] wird auf der x-Achse, die Geschwindigkeit v mit der SI-Einheit Meter pro Sekunde [m/s] auf der y-Achse abgetragen.
In dem obigen v-t-Diagramm sind zwei Geschwindigkeits-Zeit-Funktionen v1 und v2 eingezeichnet. Je höher die konstante Beschleunigung eines Körpers (z.B. Fahrzeugs) ist, desto steiler verläuft die Geschwindigkeits-Zeit-Funktion. Die Geschwindigkeits-Zeit-Funktion v2 verläuft steiler als v1, somit ist die Beschleunigung bei der Funktion v2 höher.
Aus dem v-t-Diagramm für eine gleichmäßig beschleunigte Bewegung kannst du nicht nur die Geschwindigkeit v, sondern auch die Beschleunigung a und den Weg s berechnen.
Die Steigung der v-t-Funktion zeigt die Beschleunigung ![]() an, die Fläche unterhalb der v-t-Funktion zeigt den zurückgelegten Weg
an, die Fläche unterhalb der v-t-Funktion zeigt den zurückgelegten Weg ![]() an.
an.
Video: v-t-Diagramm
Im folgenden Video betrachten wir das v-t-Diagramm und führen einige Berechnungen durch.
Beschleunigung aus der Steigung

Willst du aus dem Geschwindigkeits-Zeit-Diagramm die Beschleunigung berechnen, dann musst du nur die Steigung bestimmen. Bei einer lineare Funktion (wie oben gegeben), ist die Steigung je Zeiteinheit immer gleich groß. Betrachtest du also die obige Funktion, so siehst du sofort, dass sich die Geschwindigkeit pro Sekunde immer um 2 m/s erhöht.
Du kannst nun die Steigung berechnen, damit du die konstante Beschleunigung erhältst. Die Steigung wird wie folgt berechnet:
![]()
Die obige Gleichung zeigt dir an, wie du die Steigung berechnen kannst. Im v-t-Diagramm entspricht die Steigung der Beschleunigung a:
![]()
Zum besseren Verständnis betrachten wir die obige Geschwindigkeits-Zeit-Funktion und berechnen die Beschleunigung, indem wir die Steigung bestimmen:
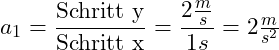
Du startest am Beginn der Funktion und gehst eine Zeiteinheit (1s) in x-Richtung. Du musst dann 2 m/s in y-Richtung gehen, damit du die Funktion wieder erreichst. Die Beschleunigung zur Geschwindigkeits-Zeit-Funktion ![]() beträgt dann:
beträgt dann:
![]()
Probe:
Du kannst die Beschleunigung natürlich ebenso mit der folgenden Gleichung berechnen:
![]()
Für diese Berechnung benötigst du die Endgeschwindigkeit v (zum Beispiel nach 3s) und die Geschwindigkeit v0 davor (zum Beispiel nach 2s). Die Zeit t ist die Geschwindigkeit zwischen den beiden gewählten Geschwindigkeiten. Wir erhalten also für t = 1s, weil genau 1 Sekunde zwischen den beiden ausgewählten Geschwindigkeiten liegt.
![]() Geschwindigkeit nach 3s
Geschwindigkeit nach 3s
![]() Geschwindigkeit nach 2s
Geschwindigkeit nach 2s
![]() Geschwindigkeitsdifferenz
Geschwindigkeitsdifferenz
Einsetzen der obigen Werte in die Gleichung ergibt:
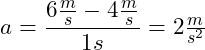
Du kannst auch als Endgeschwindigkeit ![]() (nach 4s) und als Anfangsgeschwindigkeit
(nach 4s) und als Anfangsgeschwindigkeit ![]() (nach 1s) wählen. Dann ist
(nach 1s) wählen. Dann ist ![]() , weil genau 3s zwischen den beiden ausgewählten Geschwindigkeiten liegen.
, weil genau 3s zwischen den beiden ausgewählten Geschwindigkeiten liegen.
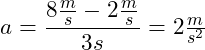
Die Beschleunigung bleibt gleich, weil eine lineare Geschwindigkeits-Zeit-Funktion gegeben ist.
Weg berechnen – Fläche unterhalb der vt-Funktion

Willst du aus dem v-t-Diagramm den zurückgelegten Weg ![]() nach einer bestimmten Zeit t berechnen, dann musst du einfach die Fläche unterhalb der Funktion berechnen. In der obigen Grafik wurde der Weg nach 3s berechnet. Dafür wurde die gesamte Fläche unterhalb der Funktion berücksichtigt. Es ergibt sich eine dreieckige Fläche. Die Fläche eines rechtwinkligen Dreiecks wird berechnet zu:
nach einer bestimmten Zeit t berechnen, dann musst du einfach die Fläche unterhalb der Funktion berechnen. In der obigen Grafik wurde der Weg nach 3s berechnet. Dafür wurde die gesamte Fläche unterhalb der Funktion berücksichtigt. Es ergibt sich eine dreieckige Fläche. Die Fläche eines rechtwinkligen Dreiecks wird berechnet zu:
![]()
Es gilt also für die obige Fläche:
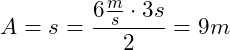
Das Fahrzeug legt in 3s einen Weg von 9m zurück.
Probe:
Zur Überprüfung verwenden wir die folgende Gleichung:
Berechnung des Weges: ![]()
Wir haben gegeben:
![]() (zu Beginn)
(zu Beginn)
![]()
![]() (aus der Steigung)
(aus der Steigung)
Einsetzen der obigen Werte in die Gleichung:
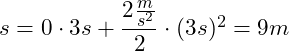
Das Fahrzeug legt also nach 3 Sekunden einen Weg von 9 Metern zurück.
Geschwindigkeit nimmt ab – Verzögerung
Im obigen Fall sind wir von einer positiven konstanten Beschleunigung und damit von einer linearen Erhöhung der Geschwindigkeit ausgegangen. Es kann natürlich ebenfalls eine negative Beschleunigung (=Verzögerung) gegeben sein. Ein Beispiel hierfür wäre ein Fahrzeug, welches sich im Bremsvorgang befindet. Bei einer Verzögerung wird die Geschwindigkeit linear verringert:

In der obigen Grafik siehst du das Geschwindigkeits-Zeit-Diagramm bei einer negativen konstanten Beschleunigung (Verzögerung). Die Anfangsgeschwindigkeit beträgt 13,89 m/s bzw. 50 km/h. Danach wird das Fahrzeug verzögert (gebremst). Die Geschwindigkeit verringert sich immer weiter, bis diese nach 5 Sekunden bei Null ist.
Beschleunigung berechnen
Das Fahrzeug wird also in diesem Beispiel bis zum Stillstand gebremst. Die Beschleunigung muss in diesem Fall negativ sein. Wir können natürlich auch hier die Beschleunigung bestimmen, entweder aus der Steigung der Funktion oder ganz einfach aus der Gleichung der Beschleunigung für die gleichmäßig beschleunigte Bewegung:
Steigung der Funktion

Du startest immer am Beginn der Funktion, in diesem Fall bei 13,89 m/s auf der y-Achse. Nun gehst du 5 Schritte (5s) in x-Richtung, wie viele Schritte musst du dann in y-Richtung gehen, um wieder bei der Funktion anzukommen? Hier musst du dann 13,89 Schritte (m/s) in negative y-Richtung gehen, deswegen resultiert ein negatives Vorzeichen. Die Beschleunigung ist also – wie zu erwarten war – negativ. Das siehst du auch sofort, da die Funktion fällt und damit eine negative Steigung vorliegt.
Alternativ verwendest du ganz einfach die folgende Gleichung:
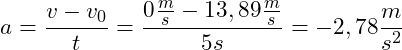
Denk daran, dass ![]() die Endgeschwindigkeit ist (hier: Null) und
die Endgeschwindigkeit ist (hier: Null) und ![]() die Anfangsgeschwindigkeit (hier: 13,89 m/s) und
die Anfangsgeschwindigkeit (hier: 13,89 m/s) und ![]() die Zeit zwischen den beiden Geschwindigkeiten.
die Zeit zwischen den beiden Geschwindigkeiten.
Weg berechnen
Den Weg kannst du – wie oben gezeigt – berechnen, indem du die Fläche unterhalb der Funktion betrachtest. Alternativ verwendest du die Gleichung für den Weg bei einer gleichmäßig beschleunigten Bewegung.
Fläche unterhalb:
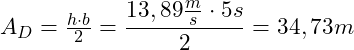
Kinematische Formel zur Berechnung des Weges:
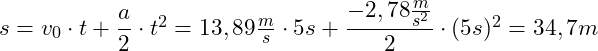
Beide Ergebnisse sind identisch.
Zusammenfassung
Schauen wir uns nochmal an, was genau die Geschwindigkeits-Zeit-Funktion bei einer gleichmäßig beschleunigten Bewegung für Informationen für dich bereit hält. Aus der Geschwindigkeits-Zeit-Funktion kannst du…
- die Geschwindigkeit zu einer bestimmten Zeit ablesen.
- die Beschleunigung aus der Steigung bestimmen.
- den zurückgelegten Weg aus der Fläche unterhalb der Funktion bestimmen.
Im nächsten Kursabschnitt betrachten wir das Weg-Zeit-Diagramm.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






