Wir betrachten in dieser Lerneinheit das Beschleunigungs-Zeit-Diagramm (auch: a-t-Diagramm) und wollen zeigen, wie du die Beschleunigung einzeichnest, was eine negative Beschleunigung ist und wie du die Geschwindigkeit aus dem a-t-Diagramm bestimmst.
Für ein optimales Verständnis helfen dir zwei anschauliche Rechenbeispiele zu dem Thema.
Dieses Thema ist ein Auszug aus unserem Onlinekurs: PH3-Kinematik
Beschleunigungs-Zeit-Diagramm: Grundlagen
Bei der gleichmäßig beschleunigten Bewegung ist eine konstante Beschleunigung (a = const) gegeben, die dazu führt, dass sich die Geschwindigkeit linear erhöht. Die Wegfunktion ist bei konstanter Beschleunigung parabelförmig.
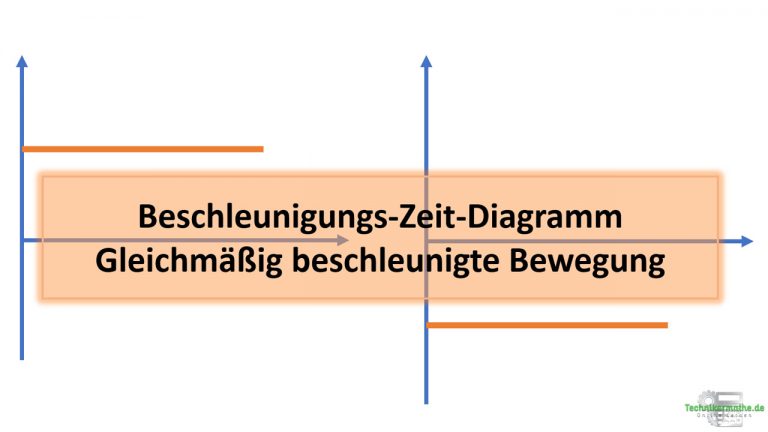
Wir starten zunächst mit dem Beschleunigungs-Zeit-Diagramm. Auf der y-Achse wird die Beschleunigung in [m/s²], auf der x-Achse die Zeit
in [s] abgetragen. Da bei einer gleichmäßig beschleunigten Bewegung die Beschleunigung
konstant ist, ergibt sich eine waagerechte Gerade:

Im obigen Diagramm sind zwei Beschleunigungs-Zeit-Funktionen und
abgebildet. Die Beschleunigungen sind konstant, d.h. sie ändern sich mit der Zeit nicht. Demnach weisen die beiden Gerade keine Steigung auf. Je höher die Gerade liegt, desto größer ist die konstante Beschleunigung.
Beschleunigung berechnen: a-t-Diagramm
Die Beschleunigung kann aus der Anfangsgeschwindigkeit und der Endgeschwindigkeit
sowie der Dauer
der beschleunigten Bewegung berechnet werden:
Geschwindigkeit berechnen: a-t-Diagramm
Es ist aber ebenfalls möglich die Geschwindigkeit aus dem a-t-Diagramm zu berechnen. Dies ist gerade für Aufgabenstellungen sinnvoll, in denen nur das a-t-Diagramm gegeben ist und du die Geschwindigkeit berechnen sollst, den der Körper (z.B. ein Auto) zu einer bestimmten Zeit während der Beschleunigung aufweist. Die Geschwindigkeit berechnest du mittels der folgenden Formeln:
Weg berechnen: a-t-Diagramm
Dir ist es ebenfalls möglich den Weg aus dem a-t-Diagramm zu berechnen, welchen das Fahrzeug während der Beschleunigung zurücklegt:
Ist also das a-t-Diagramm gegeben, so kannst du Geschwindigkeit und Weg in Abhängigkeit von der Zeit berechnen.
Beschleunigungs-Zeit-Diagramm: Fläche unterhalb der Funktion
Aus dem a-t-Diagramm kann die Geschwindigkeit auch berechnet werden, indem wir die Fläche unterhalb der Beschleunigungs-Zeit-Funktion betrachten. Zur Veranschaulichung betrachten wir im Weiteren die Beschleunigungs-Zeit-Funktion :

Die schraffierte Fläche unterhalb der Beschleunigungs-Zeit-Funktion zeigt die Geschwindigkeit an.
Zur Berechnung der aktuellen Geschwindigkeit, wird nun die Fläche unterhalb der Funktion berechnet. Es handelt sich um eine rechteckige Fläche, welche mit Höhe mal Breite berechnet werden kann.
Geschwindigkeit nach 1 Sekunde:
.
Geschwindigkeit nach 2 Sekunden:
Je weiter die Zeit verstreicht, desto größer wird die zu berechnende Fläche und desto größer ist auch die Geschwindigkeit.
Zur Ermittlung der Geschwindigkeit nach mehreren Sekunden, musst du die schraffierte Fläche unterhalb der Funktion betrachten. Willst du zum Beispiel die Geschwindigkeit nach 4 Sekunden berechnen, dann musst du die gesamte schraffierte Fläche unterhalb der Funktion von der 0. bis zur 4. Sekunde betrachten.
a-t-Diagramm: Negative Beschleunigung
Ist eine negative konstante Beschleunigung gegeben, so handelt es sich um eine Verzögerung, die dazu führt, dass die Geschwindigkeit sich linear verringert. Im a-t-Diagramm ist die Beschleunigung dann auf der negativen y-Achse gegeben:

Eine negative Beschleunigung bedeutet eine Verzögerung und damit eine Verringerung der Geschwindigkeit.
Beispiel: Beschleunigungs-Zeit-Diagramm
Schau dir im folgenden die Beschleunigungs-Zeit-Diagramme an und lösen die Aufgaben zunächst selbstständig, bevor du dir die Lösungen anschaust.
Beispiel 1 : Geschwindigkeit berechnen

Gegeben sei das obige Beschleunigungs-Zeit-Diagramm eines Fahrzeugs mit der konstanten Beschleunigung von 2,3 m/s². Die Beschleunigung dauert insgesamt 5 Sekunden.
Wie groß ist die Geschwindigkeit des Fahrzeugs
a) nach 2 Sekunden
b) am Ende der Beschleunigung
wenn das Fahrzeug eine Anfangsgeschwindigkeit von 50 km/h aufweist?
Wir suchen die Geschwindigkeit des Fahrzeugs nach 2s und am Ende der Beschleunigung (nach 5 Sekunden). Das Fahrzeug fährt vor der Beschleunigung mit einer Geschwindigkeit von 50 km/h. Danach wird das Fahrzeug mit 2,3 m/s² beschleunigt. Die Geschwindigkeit berechnen wir mittels der folgenden Formel:
ist die Beschleunigung,
die Zeit und
die Anfangsgeschwindigkeit.
Lösung a)
Zunächst wollen wir wissen, welche Geschwindigkeit das Fahrzeug nach 2 Sekunden aufweist. Wir müssen aber im 1. Schritt die Einheiten umrechnen.
1.Schritt: Einheiten umrechnen
50 km /h in m/s:
50 : 3,6 m/s = 13,89 m/s
2. Schritt: Bekannte Werte einsetzen:
3. Schritt: Einheit wieder in km/h angeben
Das Fahrzeug wird in 2 Sekunden von 50 km/h auf 66,56 km/h beschleunigt.
Lösung b)
Im Aufgabenteil b wollen wir die Geschwindigkeit am Ende der Beschleunigung bestimmen. Die Beschleunigung dauert insgesamt 5 Sekunden, damit erhalten wir:
Wir geben die Geschwindigkeit wieder im km/h an:
Das Fahrzeug weist am Ende der Beschleunigung eine Geschwindigkeit von 91,4 km/h auf.
Beispiel 2 : Weg berechnen

Gegeben sei das obige Beschleunigungs-Zeit-Diagramm eines Fahrzeugs mit der konstanter Verzögerung von 1,2 m/s². Die Verzögerung dauert insgesamt 4 Sekunden.
Welche Strecke legt das Fahrzeug
a) nach 2 Sekunden
b) am Ende der Beschleunigung
zurück, wenn das Fahrzeug eine Anfangsgeschwindigkeit von 30 km/h aufweist?
Wir suchen den Weg, welchen das Fahrzeug nach 2 Sekunden und am Ende der Verzögerung (nach 4 Sekunden) zurücklegt. Das Fahrzeug fährt vor der Verzögerung (Bremsvorgang) mit einer Geschwindigkeit von 30 km/h. Danach wird das Fahrzeug mit 1,2 m/s² verzögert. Den zurückgelegten Weg berechnen wir mittels der folgenden Formel:
ist die Beschleunigung,
die Zeit und
die Anfangsgeschwindigkeit.
Lösung a)
Zunächst wollen wir wissen, welchen Weg das Fahrzeug nach 2 Sekunden zurückgelegt hat. Wir müssen aber im 1. Schritt die Einheiten umrechnen.
1.Schritt: Einheiten umrechnen
30 km /h in m/s:
30 : 3,6 m/s = 8,33 m/s
2. Schritt: Bekannte Werte einsetzen:
Das Fahrzeug legt während des Bremsvorgangs nach 2 Sekunden 14,26 Meter zurück.
Lösung b)
Im Aufgabenteil b wollen wir den zurückgelegten Weg am Ende der Verzögerung bestimmen. Die Verzögerung dauert insgesamt 4 Sekunden, damit erhalten wir:
Das Fahrzeug hat am Ende der Verzögerung einen Weg von 23,72 m zurückgelegt bzw. der Bremsweg beträgt 23,72 m.
Wir könnten uns nun noch die Frage stellen, welche Geschwindigkeit das Fahrzeug am Ende des Bremsvorgangs aufweist? Dazu benötigen wir die folgende Gleichung:
Einsetzen der bekannten Werte:
Umgerechnet in km/h ergibt sich dann:
Das Fahrzeug weist am Ende das Bremsvorgangs eine Geschwindigkeit von 12,71 km/h auf. Das Fahrzeug wird also von 30 km/h auf 12,71 km/h abgebremst (verzögert).
Nachdem du jetzt das Beschleunigungs-Zeit-Diagramm kennengelernt hast, wollen wir uns in der nächsten Lerneinheit die Geschwindigkeits-Zeit-Funktion im v-t-Diagramm für die gleichmäßig beschleunigte Bewegung anschauen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team