PH2 – Resultierende: Zwei rechtwinklige Kräften [BEISPIEL, VIDEO, ERKLÄRUNG]

Sind zwei rechtwinklige Kräfte gegeben, so stehen die beiden Kräfte in einem 90°-Winkel zueinander. Zur Berechnung der Resultierenden kannst du den Satz des Pythagoras anwenden.

Wir betrachten in dieser Lerneinheit zwei rechtwinklige Kräfte und zeigen dir, wie du die resultierende Kraft mittels Satz des Pythagoras berechnest.

Für ein optimales Verständnis helfen dir ein Videoclip und ein ausführliches Beispiel zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Resultierende (zwei rechtwinklige Kräfte): Satz des Pythagoras

Wir betrachten in diesem Lerntext zwei Kräfte, die im rechten Winkel zueinander liegen und wollen für diese beiden Kräfte den Betrag der Resultierenden mittels Satz des Pythagoras und die Richtung der Resultierenden mittels Tangens berechnen.

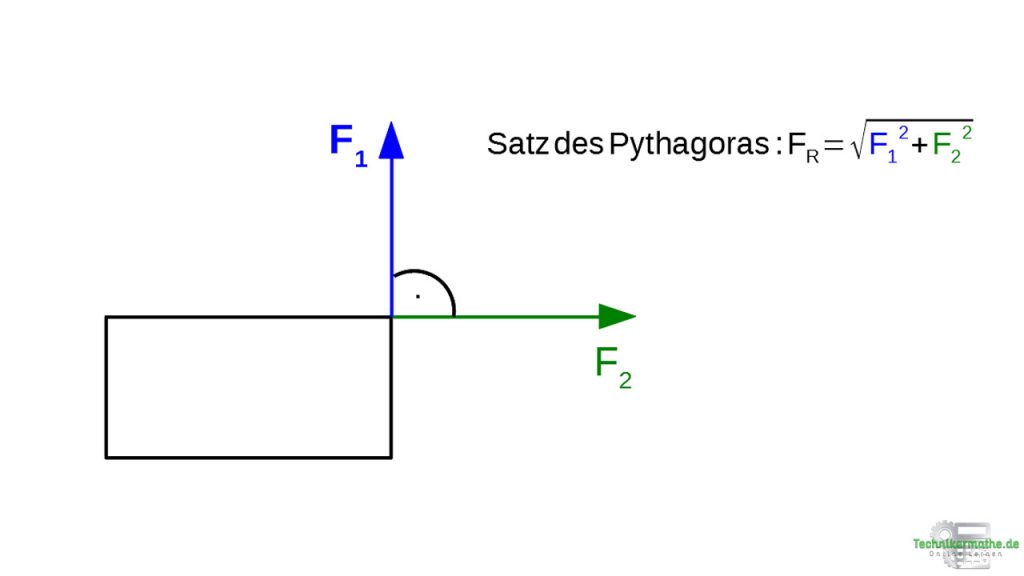
resultierende Kraft, zwei rechtwinklige Kräfte, rechtwinklige Kräfte, senkrechte Kräfte, Satz des Pythagoras, Resultierende — Zwei rechtwinklige Kräfte

Haben wir nun zwei Kräfte gegeben, die genau im 90°-Winkel zueinander liegen so können wir den Satz des Pythagoras anwenden, um die Größe der Resultierende der beiden Kräfte zu berechnen.

Resultierende mittels Satz des Pythagoras

$F_R = \sqrt{F_1^2 + F_2^2}}$

Wir können den Satz des Pythagoras auch aus dem Kosinussatz ableiten. Diesen verwenden wir, wenn wir die resultierende Kraft aus zwei Kräfte mit einem eingeschlossenen Winkel berechnen wollen. Der Kosinussatz lautet:

Resultierende mittels Kosinussatz

$F_R = \sqrt{F_1^2 + F_2^2 - 2 \cdot F_1 \cdot F_2 \cdot \cos(\beta)}$

Da die beiden Kräfte senkrecht aufeinander stehen, ist hier der Winkel mit 90° einzusetzen:

$\beta = 90^{\circ}$

Der Kosinus von 90° ergibt Null:

$\cos(90^{\circ}) = 0$

Eingesetzt in die Gleichung für den Kosinussatz ergibt sich der Satz des Pythagoras:

$F_R = \sqrt{F_1^2 + F_2^2 - 2 \cdot F_1 \cdot F_2 \cdot 0}$

$F_R = \sqrt{F_1^2 + F_2^2}$

Sind also zwei Kräfte in einem 90°-Winkel (rechtem Winkel) zueinander gegeben, dann kannst du den Satz des Pythagoras anwenden, um den Betrag der Resultierenden zu bestimmen. Alternativ kannst du auch den Kosinussatz anwenden, da aber cos(90°) = 0 ist, ergibt sich genau der Satz des Pythagoras.

Richtung der Resultierenden – Tangens

Für die Berechnung des Winkels von einer der gegebenen beiden Kräfte zur Resultierenden, kann der Tangens herangezogen werden. Wollen wir zum Beispiel den Winkel γ von der Resultierenden F_R zur Kraft F₂ berechnen, dann gilt die folgende Gleichung:

Richtung der Resultierenden aus zwei rechtwinkligen Kräften

$\tan(\gamma) = \dfrac{F_1}{F_2}}$

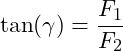
Aufgelöst nach dem Winkel γ mittels Arkustangens ( $\tan^{-1}$ ) ergibt:

$\gamma = \tan^{-1}(\dfrac{F_2}{F_1})$

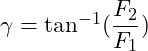
Videoclip: Resultierende aus zwei rechtwinkligen Kräften

Im folgenden Video schauen wir uns die Berechnung der resultierenden Kraft aus zwei rechtwinkligen Kräften an.

Schauen wir uns dazu ein Beispiel an.

Beispiel: Resultierende (rechtwinklige Kräfte) mittels Satz des Pythagoras

Wir schauen uns im nachfolgenden Beispiel mal an, wie der Betrag und die Richtung der Resultierenden für zwei zueinander rechtwinklige Kräfte berechnet wird.

Aufgabenstellung

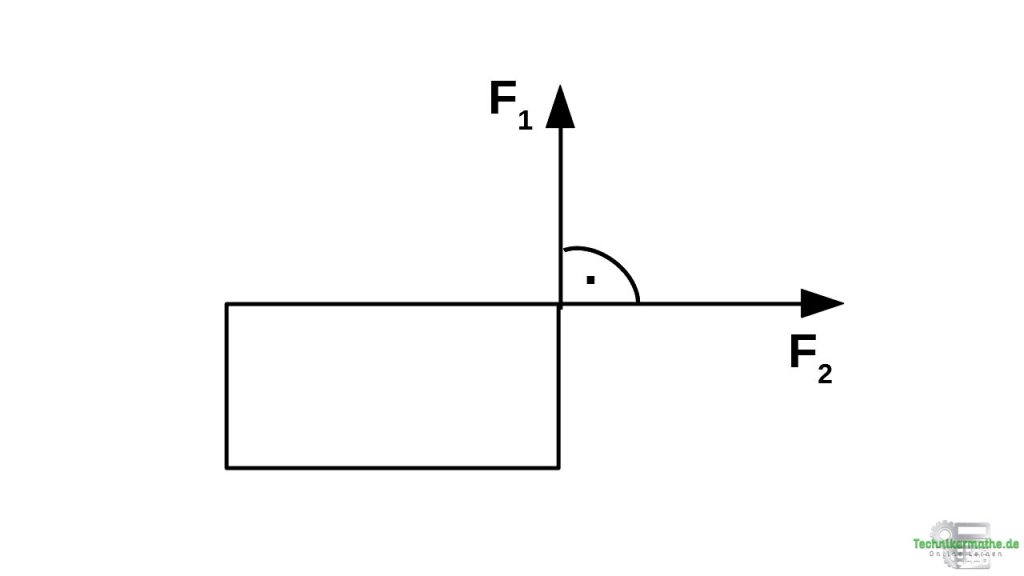
Gegeben seien die beiden Kräfte F1 = 120 N und F2 = 178 N welche rechtwinklig zueinander stehen.

Berechne die Größe und Richtung der Resultierenden!

Betrag resultierende Kraft – Satz des Pythagoras

Da beide Kräfte in einem rechten Winkel zueinander stehen, können wir zur Berechnung des Betrags der Resultierenden den Satz des Pythagoras anwenden:

$F_R = \sqrt{F_1^2 + F_2^2}$

Einsetzen der Werte:

$F_R = \sqrt{(120 N)^2 + (178 N)^2}$

$F_R = 214,67 N$

Die Größe der Resultierenden beträgt 214,67 N.

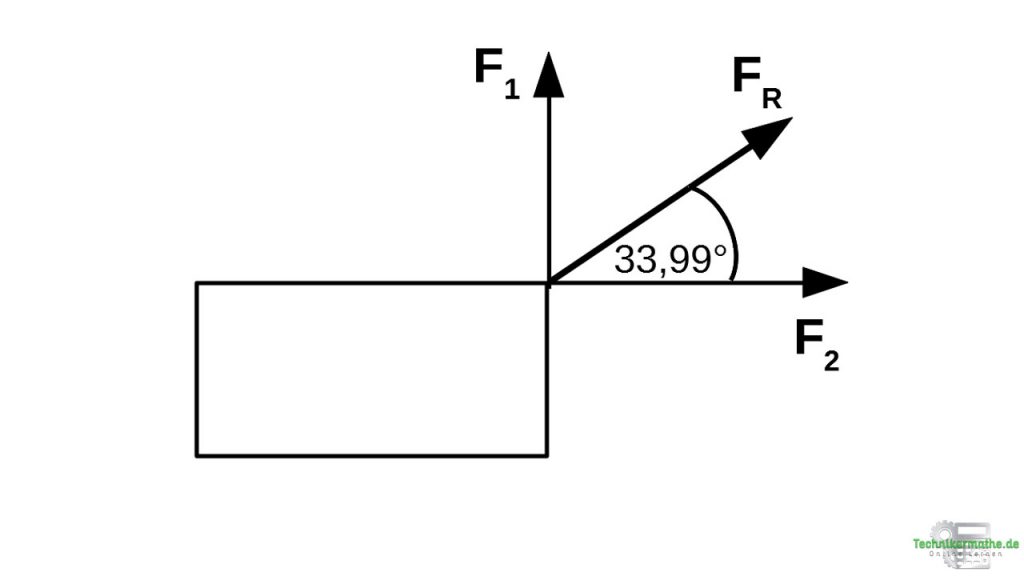
Beispiel: Resultierende mittels Satz des Pythagoras

Richtung der Resultierenden – Tangens

Als nächstes betrachten wir die Richtung der Resultierenden. Wir können hier den Tangens heranziehen, da beide Kräfte in einem rechten Winkel zueinander stehen. Wir betrachten den Winkel von der Kraft F₂ zur Resultierenden F_R:

$\tan(\gamma) = \dfrac{F_1}{F_2}$

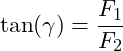
Auflösen nach dem Winkel γ:

$\gamma = \tan^{-1}(\dfrac{F_1}{F_2})$

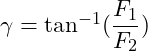
Einsetzen der Werte:

$\gamma = \tan^{-1}(\dfrac{120 N}{178 N})$

$\gamma = 33,99^{\circ}$

Der Winkel von der Resultierenden F_R zur Kraft F₂ beträgt 33,99°.

Was kommt als Nächstes?

Nachdem du jetzt weißt wie man die Resultierende mittels Satz des Pythagoras bestimmt, betrachten wir in der folgenden Lerneinheit ausführlich die Zerlegung einer Kraft in zwei Kraftkomponenten (Kräftezerlegung).

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++