PH2 – Prüfungsaufgaben: Betrag und Richtung der Resultierenden aus zwei Kräften

In dieser Lerneinheit betrachten wir zwei Aufgaben mit ausführlichen Lösungswegen, in denen du lernen sollst die Resultierende aus zwei Kräften unter Anwendung des Kosinussatzes und des Sinussatzes zu bestimmen.

Warum wird überhaupt eine resultierende Kraft berechnet?

Die resultierende Kraft ersetzt die beiden gegebenen Kräfte. Wenn du die Größe (den Betrag) und die Richtung der Resultierenden $F_R$ kennst, dann kannst du die beiden gegebenen Kräfte durch die Resultierende ersetzen. Du benötigst dann also nur noch eine Kraft, anstelle von zwei Kräften!

Wir betrachten zwei Aufgaben mit ausführlicher Lösung zur Berechnung von Betrag und Richtung der Resultierenden aus zwei Kräften.

Für ein optimales Verständnis helfen dir drei unterschiedliche Beispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Wir haben bereits in den vorherigen Lernabschnitten ausführlich gezeigt, wie du die Richtung und den Betrag der resultierenden Kraft aus zwei Kräften mittels Kosinussatz und Sinussatz berechnest. Damit du das Erlernte auch festigen kannst, schauen wir uns mal zwei Aufgaben mit ausführlichen Lösungswegen an.

Du sollst in den nachfolgenden beiden Aufgaben den Betrag und die Richtung der Resultierenden aus zwei Kräften mittels Kosinussatz und Sinussatz bestimmen. Versuche zunächst die Aufgaben selbstständig zu lösen. Solltest du nicht weiter wissen, kannst du dir die Lösungen dazu anschauen.

Beispiel 1: Resultierende aus zwei Kräften

Aufgabenstellung

Resultierende aus zwei Kräften, Aufgaben, Lösung, Beispiel, Resultierende, zwei Kräfte, Kosinussatz, Sinussatz — Beispiel: Resultierende aus zwei Kräften

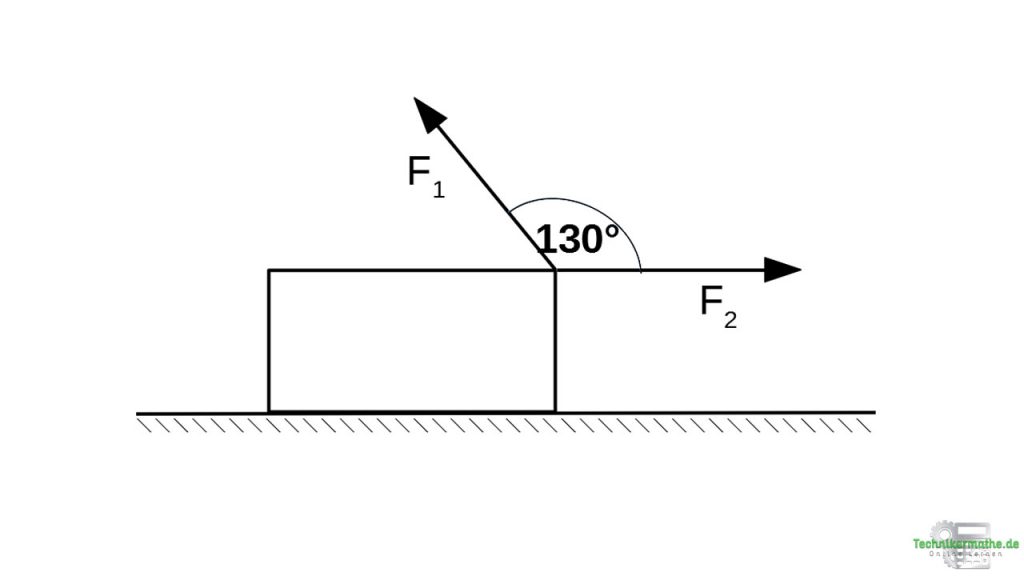
Gegeben seien die beiden Kräfte F₁ = 80 N und F₂ = 180 N, welche auf eine Kiste wirken. Die beiden Kräfte sollen durch eine einzige Kraft ersetzt werden.

Wie groß muss dieses Kraft sein und in welche Richtung muss sie wirken (Winkel zur Horizontalen).

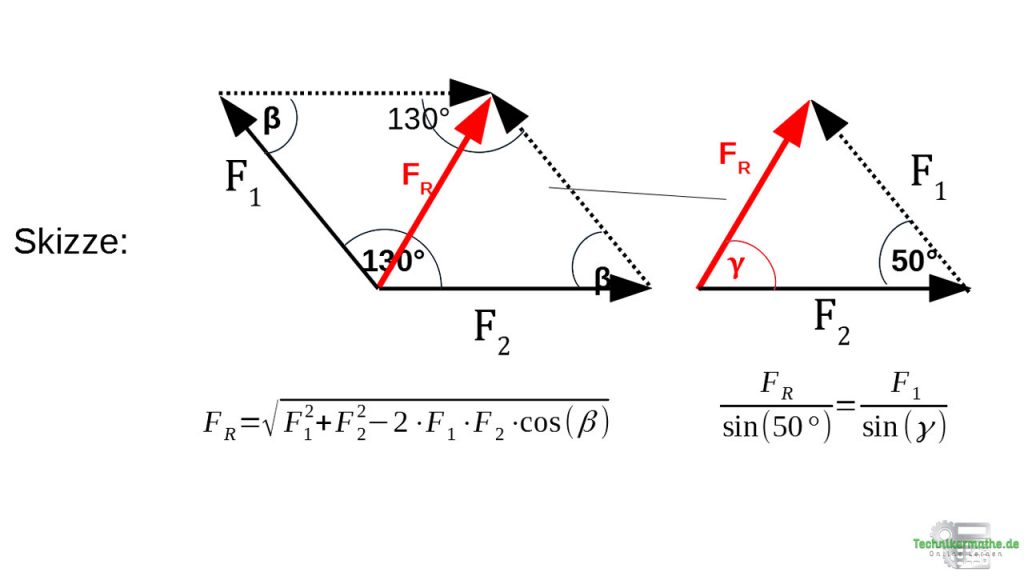
Resultierende aus zwei Kräften, Kräfteparallelogramm, Kosinussatz, Aufgabe, Lösung, Beispiel — Berechnung des Betrags der Resultierenden mittels Kosinussatz

Betrag der Resultierenden – Kosinussatz

Wir skizzieren zunächst das Kräfteparallelogramm (siehe obige linke Grafik). Danach wenden wir den Kosinussatz an:

$F_R = \sqrt{F_1^2 + F_2^2 - 2 \cdot F_1 \cdot F_2 \cdot \cos(\beta)}$

Berechnung des Winkels β:

$360^{\circ} - 2 \cdot 130^{\circ} = 2 \beta$

$\beta = 50^{\circ}$

Einsetzen der bekannten Werte:

$F_R = \sqrt{(80 N)^2 + (180)^2 - 2 \cdot 80 N \cdot 180 N \cdot \cos(50^{\circ})}$

$F_R = 142,4 N$

Die resultierende Kraft muss mit einer Kraft von 142,43 N angebracht werden, um die beiden anderen Kräfte zu ersetzen.

Richtung der Resultierenden – Sinussatz

Die Richtung zur Horizontalen (also zur Kraft F₂) berechnen wir mittels Sinussatz (siehe rechte obige Grafik):

$\frac{F_1}{\sin(\gamma)} = \frac{F_R}{\sin(50^{\circ})}$

Nach dem gesuchten Winkel γ auflösen:

$\frac{\sin(\gamma)}{F_1} = \frac{\sin(50^{\circ})}{F_R}$

$\sin(\gamma) = \frac{\sin(50^{\circ})}{F_R} \cdot F_1$

$\gamma = \sin^{-1}(\frac{\sin(50^{\circ})}{F_R} \cdot F_1)}$

Werte einsetzen:

$\gamma = \sin^{-1}(\frac{\sin(50^{\circ})}{142,4 N} \cdot 80 N) = 25,5^{\circ}$

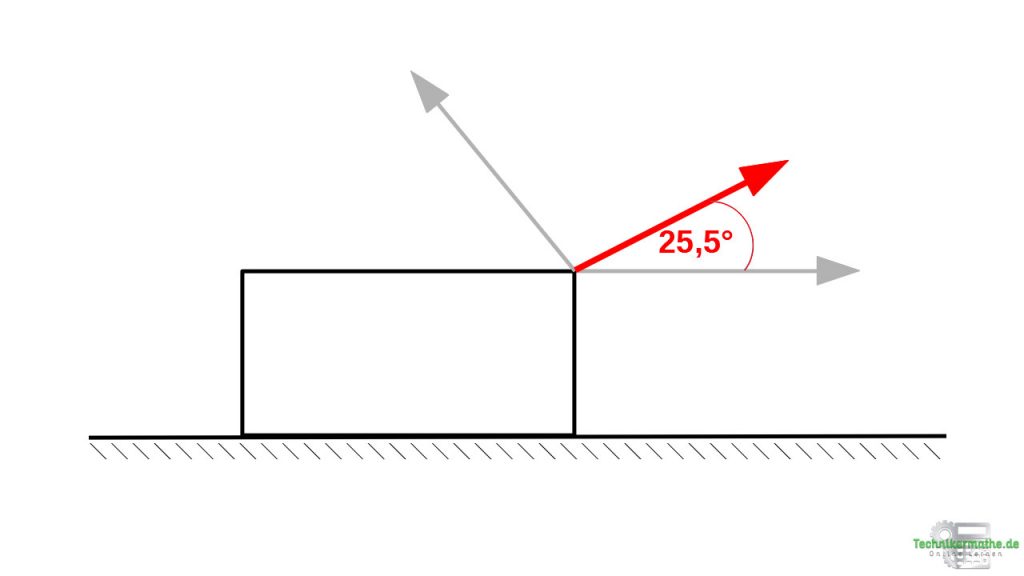
Die Resultierende muss mit einer Kraft von 142,4 N und einem Winkel von 25,5° zur Horizontalen (zur Kraft F₂) angebracht werden, damit sie dieselbe Wirkung wie die beiden Kräfte F₁und F₂ausübt.

Resultierende aus zwei Kräften, Aufgaben, Lösungen, Resultierende — Ergebnis: Resultierende aus zwei Kräften

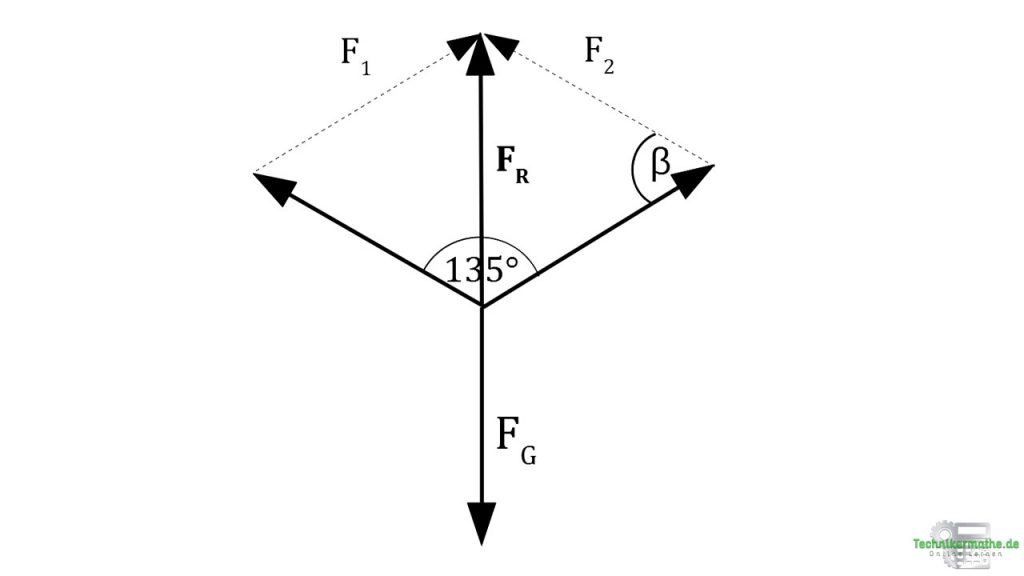
Beispiel 2: Betrag und Richtung der Resultierenden aus zwei Kräften

Aufgabenstellung

Resultierende, Kneipenschild, Resultierende aus zwei Kräften, Schild — Aufgabe: Resultierende aus zwei Kräften – Hängendes Schild

Gegeben sei das Kneipenschild, welches mittels zwei Seilen an der Decke befestigt ist. Die Seile üben jeweils eine Zugkraft von 150 N aus.

Wie groß ist die Gewichtskraft F_G des Schildes?

Die Summe der beiden Kräftemuss der Gewichtskraft F_G entsprechen, um das Schild zu halten. Demnach muss die resultierende Kraft ganz alleine die Gewichtskraft des Schildes tragen. Also muss die Resultierende genau so groß sein, wie die Gewichtskraft des Schildes:

$F_G = F_R$

Die Richtung der Resultierenden ist in diesem Beispiel bereits vorab bekannt. Da die Gewichtskraft F_G immer vertikal nach unten gerichtet ist, muss die resultierende Kraft vertikal nach oben gerichtet sein. Also genau entgegengesetzt, damit die resultierende Kraft auch das Kneipenschild mit der Gewichtskraft F_G halten kann.

Kneipenschild, Resultierende, hängendes Schild, Aufgabe, Lösung, Kräfteparallelogramm, Gewichtskraft — Bestimmung der Resultierenden

Der Kosinussatz lautet:

$F_R = \sqrt{F_1^2 + F_2^2 - 2 \cdot F_1 \cdot F_2 \cdot \cos(\beta)}$

Den Winkel β berechnen wir wie folgt:

$360^{\circ} - 2 \cdot 135^{\circ} = 2 \cdot \beta$

$90^{\circ} = 2 \cdot \beta$

$\beta = 45^{\circ}$

Einsetzen der Werte:

$F_R = \sqrt{(150N)^2 + (150N)^2 - 2 \cdot 150N \cdot 150N \cdot \cos(45^{\circ})}$

$F_R = 114,81 N$

Die beiden Seile zusammen tragen eine Kraft von 114,81 N. Dies entspricht der Gewichtskraft des Bildes.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++