PH2 – Schwerpunkt zusammengesetzter Körper [Erklärung, Beispiel, Formel]

Der Schwerpunkt zusammengesetzter Flächen kann durch die Aufteilung der Fläche in einfachere Formen bestimmt werden. Zuerst wird die Fläche in Teilbereiche aufgeteilt, für die der Schwerpunkt bekannt ist, wie z.B. Rechtecke, Dreiecke oder Kreissegmente. Dann wird die Schwerpunktlage dieser Teilbereiche berechnet und gewichtet, um den Gesamtschwerpunkt zu finden.

In dieser Lerneinheit schauen wir uns an, wie man den Schwerpunkt zusammengesetzter Körper berechnet. Wir betrachten hierzu ein ausführlichen Beispiels zur Berechnung des Gesamtschwerpunkts eines U-Profils.

Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.

Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs PH2-Einführung in die Statik

Schwerpunkt zusammengesetzten Körper

Häufig sind Körper aus mehreren Teilen zusammengesetzt. Willst du für einen solchen Körper den Gesamtschwerpunkt bestimmen, dann kannst du die Fläche des Körpers in einfache geometrische Teilflächen aufteilen, für welche du die Schwerpunktlage kennst. Aus der Lage dieser Einzelschwerpunkte kannst du dann die Lage des Schwerpunktes für den gesamten Körper bestimmen.

Berechnung: Schwerpunkt am U-Profil

Wir schauen uns jetzt mal an, wie du den Schwerpunkt zusammengesetzter Flächen bestimmen kannst. Dazu betrachten wir das folgende U-Profil:

Schwerpunkt zusammengesetzter Flächen, Schwerpunkt, U Profil, Beispiel, Flächenschwerpunkt, zusammengesetzte Fläche — Gesamtschwerpunkt bestimmen

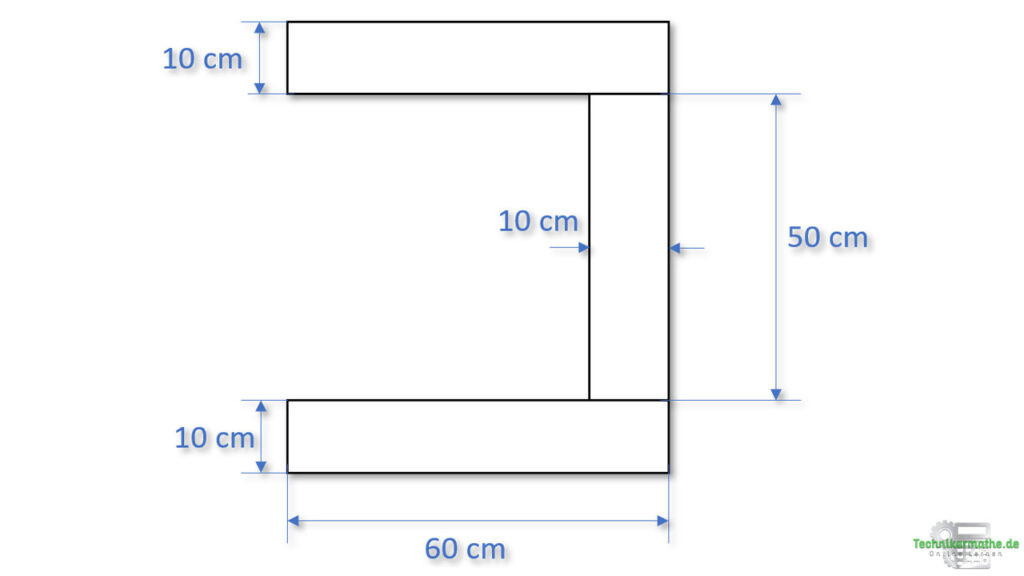
In der obigen Grafik ist näherungsweise ein U-Profil zu sehen. Wir suchen den Gesamtschwerpunkt dieses Profils. Dazu teilst du das gegebene Profil in mehrere Teilflächen, von denen du die Schwerpunktlage kennst. So weißt du zum Beispiel, dass die Schwerpunkte von Rechtecken, Quadraten und eines Kreisen in der Mitte liegen. Das obige Profil kannst du so zum Beispiel in drei rechteckige Flächen aufteilen und die Schwerpunkte genau mittig einzeichnen:

Schwerpunkt zusammengesetzter Flächen, Beispiel, Teilflächen, Schwerpunkt, Fläche, U-Profil, Schwerpunkt zusammengesetzter Körper — Gesamtschwerpunkt bestimmen: Teilflächen festlegen

Der erste Schritt ist also die Gesamtfläche in Teilflächen aufzuteilen, von denen du die Lage der Schwerpunkte kennst. In der obigen Grafik haben wir nun die Gesamtfläche in drei rechteckige Teilflächen aufgeteilt. Die Schwerpunkte liegen jeweils in der Mitte. Du kannst dazu zusätzlich die Abmessungen des Schwerpunktes eintragen, wenn du möchtest (so wie in der Grafik geschehen). Außerdem solltest du die Teilflächen durchnummerieren, damit du bei den Berechnungen die Übersicht behältst.

Der nächste Schritt ist nun ein Koordinatensystem festzulegen, falls nicht bereits eines in der Aufgabenstellung gegeben. Wenn kein Koordinatensystem gegeben ist, kannst du dir die Lage des Koordinatensystems selbst aussuchen. Dabei ist es sinnvoll das Koordinatensystem immer links unten an den Körper zu setzen, da du dich bei der Berechnung dann immer in positive Achsenrichtungen bewegst und so die Abstände immer positiv sind.

Schwerpunkt zusammengesetzter Flächen, Schwerpunkt einer Fläche, Flächenschwerpunkt, U-Profil, Beispiel, Schwerpunkt zusammengesetzter Körper — Gesamtschwerpunkt bestimmen: Koordinatensystem festlegen

Formeln: Schwerpunkt zusammengesetzter Körper

Nachdem du diese Schritte durchgeführt hast, können wir mit der Berechnung starten. Du benötigst dazu die folgenden beiden Gleichungen:

$x_S = \dfrac{\sum x_i \cdot A_i}{\sum A_i}$ Abstand in x-Richtung

$y_S = \dfrac{\sum y_i \cdot A_i}{\sum A_i}$ Abstand in y-Richtung

$x_S$ ist hierbei der Abstand vom Koordinatensystem zum Gesamtschwerpunkt in x-Richtung und $y_S$ der Abstand vom Koordinatensystem zum Gesamtschwerpunkt in y-Richtung. $x_i$ bzw. $y_i$ ist der Abstand vom Koordinatensystem zu den Schwerpunkten der Teilflächen in x-Richtung bzw. y-Richtung, $A_i$ ist die jeweilige Teilfläche. $\sum$ ist das Summenzeichen. Wir haben insgesamt drei Teilflächen gegeben, weshalb du die obigen Gleichungen wie folgt schreiben kannst:

$x_S = \dfrac{\sum x_i \cdot A_i}{\sum A_i} = \dfrac{x_1 \cdot A_1 + x_2 \cdot A_2 + x_3 \cdot A_3}{A_1 + A_2 + A_3}$

$y_S = \dfrac{\sum y_i \cdot A_i}{\sum A_i} = \dfrac{y_1 \cdot A_1 + y_2 \cdot A_2 + y_3 \cdot A_3}{A_1 + A_2 + A_3}$

Wir können nun damit beginnen die Schwerpunktlage des gegebenen Profils zu bestimmen.

Flächenschwerpunkt: Teilfläche 1

Gesamtschwerpunkt, Teilfläche, U-Profil, Schwerpunkt berechnen, Beispiel, Schwerpunktlage, Schwerpunkt zusammengesetzter Körper — Schwerpunkt: Teilfläche 1

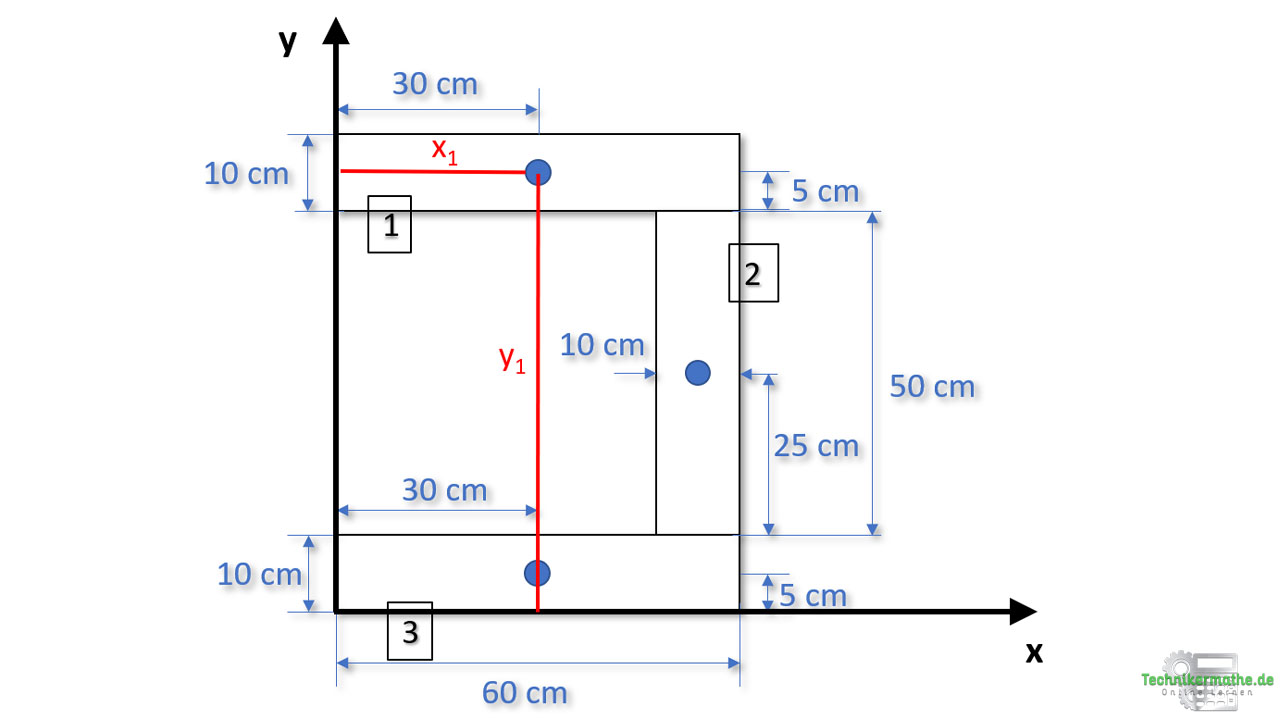
Wir starten mit der Teilfläche 1 und berechnen die Abstände vom Koordinatenursprung in x-Richtung ( $x_1$ ) und in y-Richtung ( $y_1$ ) sowie den Flächeninhalt $A_1$ .

$x_1$ Abstand vom Koordinatensystem zum Schwerpunkt der Teilfläche 1 in x-Richtung

$y_1$ Abstand vom Koordinatensystem zum Schwerpunkt der Teilfläche 1 in y-Richtung

$A_1$ Flächeninhalt der Teilfläche 1

Merk’s dir!

Bei der Berechnung musst du immer darauf achten, ob du dich in negative oder positive Achsenrichtung bewegst und die Vorzeichen in jedem Fall mitberücksichtigen. Da wir das Koordinatensystem nach links unten gelegt haben, bewegen wir uns immer in positive Achsenrichtung.

Der Abstand in x-Richtung vom Koordinatensystem zum Schwerpunkt der Teilfläche 1 beträgt:

$x_1 = 30 cm$

Der Abstand in y-Richtung vom Koordinatensystem zum Schwerpunkt der Teilfläche 1 beträgt:

$y_1 = 10 cm + 50 cm + 5 cm = 65 cm$

Der Flächeninhalt beträgt:

$A_1 = 10 cm \cdot 60 cm = 600 cm^2$

Flächenschwerpunkt: Teilfläche 2

Gesamtschwerpunkt, Teilfläche, U-Profil, Beispiel, Berechnung, Schwerpunkt berechnen, Schwerpunkt, — Schwerpunkt: Teilfläche 2

Danach betrachten wir Teilfläche 2 und berechnen die Abstände vom Koordinatensystem in x-Richtung ( $x_2$ ) und in y-Richtung ( $y_2$ ) sowie den Flächeninhalt $A_2$ .

$x_2$ Abstand vom Koordinatensystem zum Schwerpunkt der Teilfläche 2 in x-Richtung

$y_2$ Abstand vom Koordinatensystem zum Schwerpunkt der Teilfläche 2 in y-Richtung

$A_2$ Flächeninhalt der Teilfläche 2

Der Abstand in x-Richtung vom Koordinatensystem zum Schwerpunkt der Teilfläche 2 beträgt:

$x_2 = 60 cm - 5cm = 55 cm$

Der Abstand in y-Richtung vom Koordinatensystem zum Schwerpunkt der Teilfläche 2 beträgt:

$y_2 = 10 cm + 25 cm = 35 cm$

Der Flächeninhalt beträgt:

$A_2 = 10 cm \cdot 50 cm = 500 cm^2$

Flächenschwerpunkt: Teilfläche 3

Gesamtschwerpunkt, Teilfläche, U-Profil, Beispiel, Schwerpunkt, Flächenschwerpunkt, Berechnung — Schwerpunkt: Teilfläche 3

Als letztes betrachten wir die Teilfläche 3:

$x_3$ Abstand vom Koordinatensystem zum Schwerpunkt der Teilfläche 3

$y_3$ Abstand vom Koordinatensystem zum Schwerpunkt der Teilfläche 3

$A_3$ Flächeninhalt der Teilfläche 3

Der Abstand in x-Richtung vom Koordinatensystem zum Schwerpunkt der Teilfläche 3 beträgt:

$x_3 = 30 cm$

Der Abstand in y-Richtung vom Koordinatensystem zum Schwerpunkt der Teilfläche 3 beträgt:

$y_3 = 5 cm$

Der Flächeninhalt beträgt:

$A_3 = 60 cm \cdot 10 cm = 600 cm^2$

Gesamtschwerpunkt ermitteln

Wir können nun die obigen Gleichungen anwenden und die Schwerpunktlage des Gesamtprofils bestimmen.

Abstand in x-Richtung vom Koordinatenursprung zum Schwerpunkt:

$x_S = \dfrac{x_1 \cdot A_1 + x_2 \cdot A_2 + x_3 \cdot A_3}{A_1 + A_2 + A_3}$

$x_S = \dfrac{30 cm \cdot 600 cm^2 + 55 cm \cdot 500 cm^2 + 30 cm \cdot 600 cm^2}{600 cm^2 + 500 cm^2 + 600 cm^2}$

$x_S = 37,35 cm$

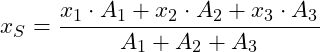
Abstand in y-Richtung vom Koordinatenursprung zum Schwerpunkt:

$y_S = \dfrac{y_1 \cdot A_1 + y_2 \cdot A_2 + y_3 \cdot A_3}{A_1 + A_2 + A_3}$

$y_S = \dfrac{65 cm \cdot 600 cm^2 + 35 cm \cdot 500 cm^2 + 5 cm \cdot 600 cm^2}{600 cm^2 + 500 cm^2 + 600 cm^2}$

$y_S = 35 cm$

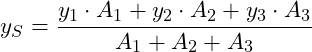
Der Abstand vom Koordinatensystem zum Gesamtschwerpunkt in x-Richtung beträgt 37,35 cm und in y-Richtung 35 cm:

Gesamtschwerpunkt: Lage in einem U-Profil, U-Profil, Gesamtschwerpunkt — Lage des Gesamtschwerpunktes

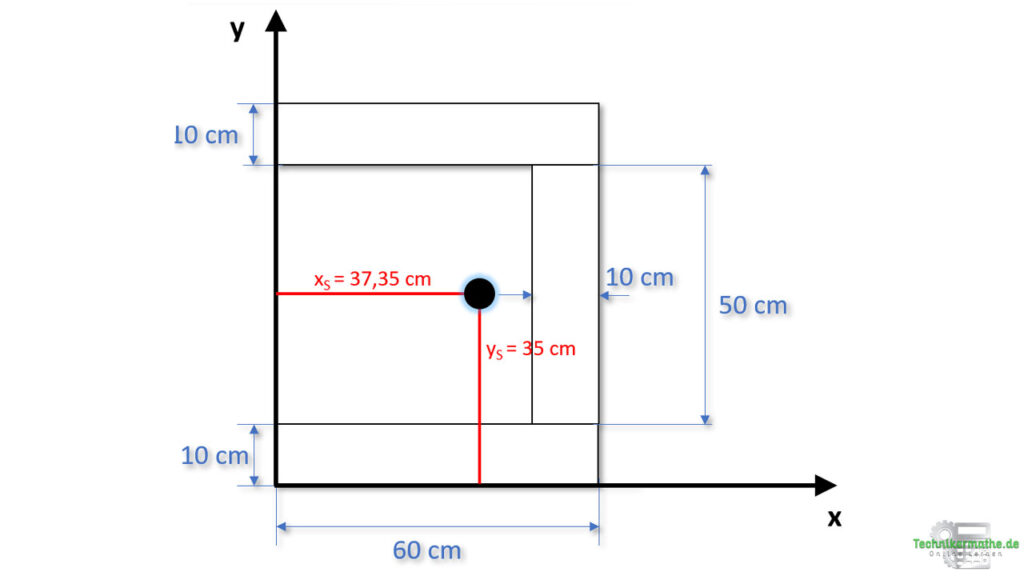
Der Gesamtschwerpunkt ist also bestimmt und liegt außerhalb des Körpers.

Du siehst also, dass es auch Körper gibt, deren Schwerpunkt außerhalb des Körpers liegt. Dies ist auch zum Beispiel bei einem Bumerang der Fall. Hängst du den Körper in seinem Schwerpunkt auf oder unterstützt du den Schwerpunkt, so befindet sich der Körper im Gleichgewicht: Er bewegt sich weder vertikal noch horizontal noch rotiert er.

Learning by doing!…

Zum besseren Verständnis kannst du ganz einfach das folgende sehr einfach Experiment durchführen. Dazu benötigst du lediglich einen Stift, ein Lineal, eine Schere, eine Pappe (Schuhkarton oder ähnliches) und ein dünnes Blatt Papier. Zeichne das obige Profil auf eine Pappe. Du kannst die obigen Maße auch halbieren/vierteln, damit es besser auf die Pappe passt.

Schneide das Profil dann aus. Als nächstes klebst du ein dünnes Blatt Papier unter das Profil. Das dünne Blatt Papier hat kaum Eigengewicht, so dass dieses einen vernachlässigbaren Einfluss auf den Gesamtschwerpunkt hat. Du kannst nun mit einem Stift den Schwerpunkt am Blatt Papier suchen. Suche den Schwerpunkt ungefähr an der von uns bestimmten Position. Sobald das Profil nicht von dem Stift herunterfällt, hast du den Schwerpunkt gefunden. Übrigens: Das dünne Blatt Papier benötigst du, weil der Schwerpunkt außerhalb des Profils liegt.

Schwerpunkt experimentell ermitteln — Schwerpunkt selbst bestimmen

Was kommt als Nächstes?

In der nächsten Lerneinheit stellen wir dir ausführliche Beispiele zur Berechnung der Schwerpunktlage für zusammengesetzte Profile vor.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++