Der Flächenschwerpunkt, auch geometrischer Schwerpunkt genannt, ist ein wichtiger Begriff in der Geometrie und Ingenieurwissenschaften. Er ist der Punkt, an dem sich die gesamte Fläche gleichmäßig zu verteilen scheint und um den sie sich im Gleichgewicht befindet. In einfachen Formen wie Rechtecken, Dreiecken oder Kreisen ist der Schwerpunkt leicht zu bestimmen.
Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.
Mehr zu diesem Thema und der Statik findest du in unserem Onlinekurs TM1-Statik.
Flächenschwerpunkte
Schau dir das obige Bild mal an. Du wirst ein solches Bild bestimmt schon häufiger gesehen haben oder du hast bereits selbst versucht, Steine übereinander zu stapeln. Wenn nicht, dann wäre jetzt der richtige Zeitpunkt dafür, denn die obigen Steine liegen alle mit ihren Schwerpunkten aufeinander. Du musst also lediglich durch probieren herausfinden, wo genau der Schwerpunkt eines Steins liegt. Du hast diesen gefunden, wenn der Stein ruhig aufliegt, sich also nicht bewegt.
- Der Schwerpunkt (auch : Massenmittelpunkt) eines Körpers ist derjenige Punkt, den man sich als Angriffspunkt der Schwerkraft (also der Gewichtskraft) vorstellen kann.
Du hast bereits in den vorangegangenen Lerneinheiten die Gewichtskraft kennengelernt, die infolge der Schwerkraft (g = 9,81 m/s² ) entsteht. Du hast auch gelernt, dass die Gewichtskraft immer im Schwerpunkt des Körpers angreift.
Wird ein fester Körper in seinem Schwerpunkt aufgehängt oder abgestützt, so verbleibt er in seiner Lage, ohne eine Drehbewegung auszuführen. Das bedeutet also, dass ein Drehmoment, das im Schwerpunkt angreift, wirkungslos ist.
Wenn du ein Bild an einem Nagel aufhängen willst, dann musst du auch den Schwerpunkt des Bildes treffen, zumindest den waagrechten Abstand. Wenn wir also von einem rechteckigen Bilderrahmen ausgehen, so liegt der Schwerpunkt in der Mitte. Du musst das Bild also genau mittig aufhängen, damit es gerade hängt. Eine kleine Abweichung führt dazu, dass das Bild anfängt zu kippen.
Übersicht: Schwerpunkte verschiedener Flächen
In der nachfolgenden Grafik siehst du die Schwerpunktlage sowie die Berechnung der Fläche für Rechtecke, Quadrate, Kreise und Parallelogramme:
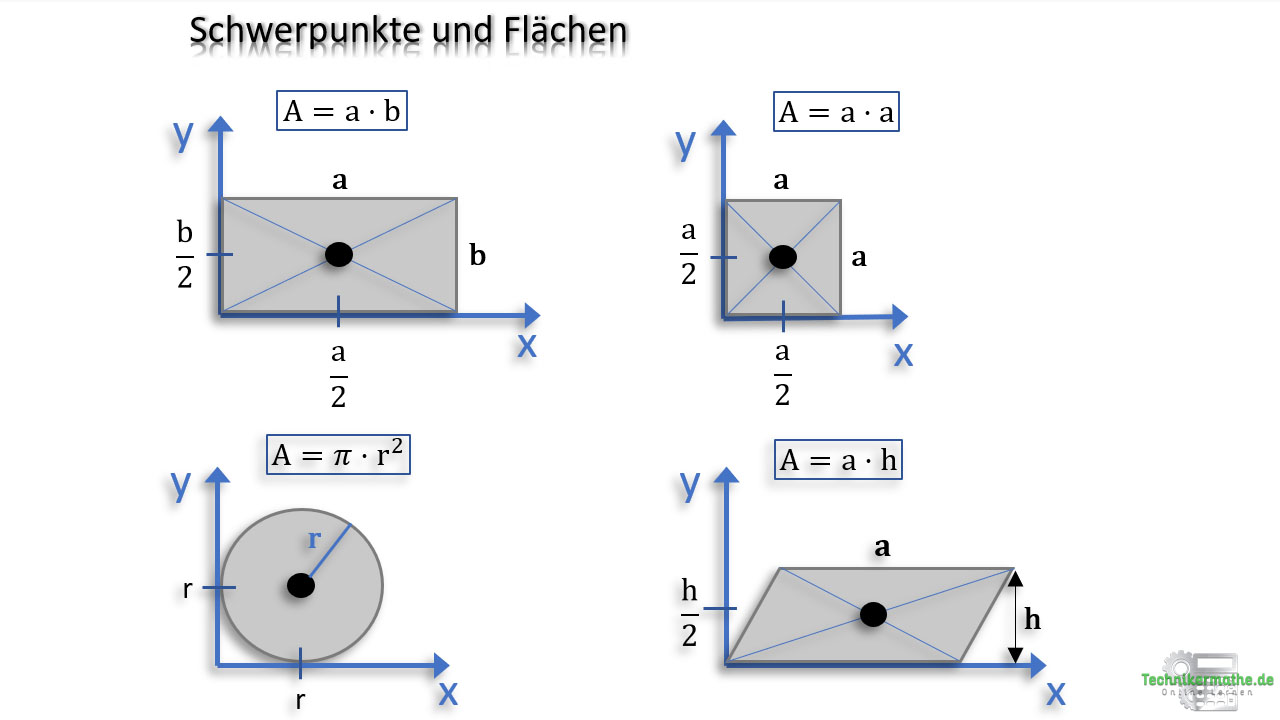
Bei einem Rechteck und Quadrat liegt der Schwerpunkt genau in der Mitte im Schnittpunkt der Diagonalen. Ein weiterer Körper, bei welchem sich der Schwerpunkt genau in der Mitte befindet, ist der Kreis. Hier liegt der Schwerpunkt im Abstand vom Radius r zum Kreisrand. Beim Parallelogramm liegt der Schwerpunkt – wie beim Rechteck und Quadrat – im Schnittpunkt der Diagonalen. Der Abstand in y-Richtung liegt bei der Hälfte der senkrechte Höhe h.
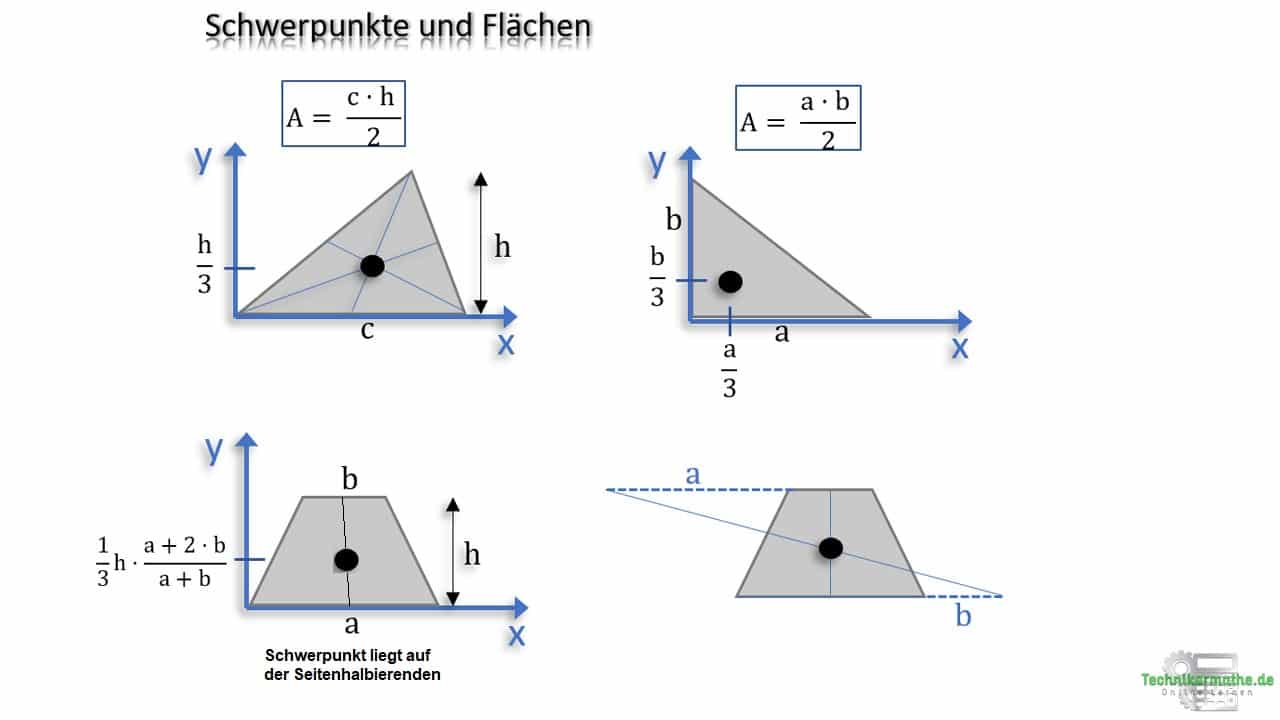
In der obigen Grafik ist die Schwerpunktlage eines allgemeinen Dreiecks (links oben) sowie eines rechtwinkligen Dreiecks (rechts oben) gegeben. Den Schwerpunkt eines allgemeinen Dreiecks kannst du bestimmen, indem du die Seitenhalbierenden einzeichnest. Im Schnittpunkt der Seitenhalbierenden liegt der Schwerpunkt. Für rechtwinklige Dreiecke gilt, dass der Schwerpunkt ausgehend vom rechten Winkel bei 1/3 der Höhe und Breite des Dreiecks liegt.
Für ein Trapez kannst du den Schwerpunkt entweder über die obigen Gleichungen berechnen (links unten) oder aber du ermittelst den Schwerpunkt zeichnerisch (rechts unten). Dazu musst du die untere Seite a oben an die Seite b anfügen und die Seite b an die untere Seite a (genau in die andere Richtung). Dann verbindest du beide Endpunkte miteinander. Danach zeichnest du eine Gerade von der Mitte der Seite b zur Mitte der Seite a.
Nachdem du jetzt die Schwerpunkte einer Fläche kennengelernt hast, wollen wir uns in der nachfolgenden Lerneinheit mal anschauen, wie man den Schwerpunkt eines zusammengesetzten Körpers ganz einfach berechnet.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team







