PH2 – Federkraft und Federkonstante [Beispiel, Video, Erklärung]

In dieser Lerneinheit erklären wir dir ausführlich und einfach was es mit der Federkraft auf sich hat und was die Federkonstante ist.

Für ein optimales Verständnis helfen dir ein drei ausführlich gelöste Beispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Federkraft und Federkonstante – Definition

Die Federkraft entsteht, wenn ein elastischer Körper wie eine Feder auseinandergezogen oder zusammengedrückt wird. In dem elastischen Körper wirkt eine entgegengesetzte Kraft, welche die Feder wieder in die Ausgangsposition zurückversetzen möchte.

Die Federkonstante, auch Federsteifigkeit, Federhärte, Federrate, Richtgröße oder Direktionskonstante genannt, beschreibt das Verhältnis der auf eine Feder wirkenden Kraft zur dadurch bewirkten Auslenkung der Feder.

Schraubenfeder, Feder, Federkraft, Federkonstante — Schraubenfeder beim Zug

Die Gleichungen für die Federkraft sind ein wichtiges Thema in der technischen Mechanik, da diese auch auf andere elastische Körper angewendet werden können. Schauen wir uns also die Berechnung der Federkraft und Federkonstante an.

Federkraft, Federkonstante, Übersicht, Auslenkung, Gewichtskraft, Feder, Schraubenfeder, Ruhelage, Federsteifigkeit, rückwirkende Kraft — Federkraft im Überblick

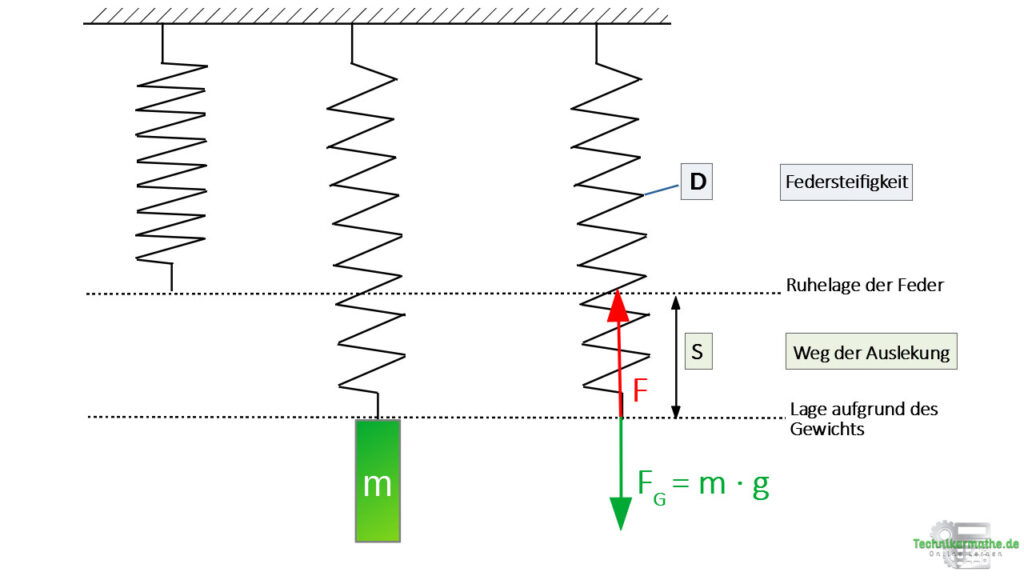
In der obigen Grafik ist eine Schraubenfeder abgebildet, welche sich zunächst ohne Gewicht in der Ruhelage befindet. Wird die Feder nun durch ein Gewicht ausgelenkt, so ändert die Feder ihre Position. Sie weist nun eine neue Lage auf, die aufgrund des Gewichts mit der Masse m entstanden ist.

Der Weg, um welche die Feder ausgelenkt wird, wird mit dem Buchstaben s bezeichnet:

$s$ Weg der Auslenkung

Das Gewicht kann durch die Gewichtskraft F_G ersetzt werden. Eine Gewichtskraft wirkt immer vertikal nach unten und wird wie folgt berechnet:

$F_G = m \cdot g$ Gewichtskraft

Bei einer Feder wirkt immer eine sogenannte rückwirkende Federkraft F. Diese rückwirkende Federkraft wirkt der Kraft der Auslenkung genau entgegen. In der obigen Grafik wird die Feder mittels eines Gewichts nach unten hin ausgelenkt. Wird nun das Gewicht wieder entfernt, so zieht sich die Feder infolge der rückwirkenden Kraft $F$ wieder zurück in ihre Ausgangslage. Dabei ist die rückwirkende Kraft genau so groß wie die Gewichtskraft:

$F_G = F$

Berechnung der Federkraft

Du weißt nun also, dass die rückwirkende Federkraft und die Kraft der Auslenkung genau gleich groß sind. Du kannst die Federkraft aber auch aus der Federkonstante $D$ und dem Weg der Auslenkung $s$ berechnen:

$F = D \cdot s$ Federkraft

mit

$D$ Federkonstante [N/m]

$s$ Weg der Auslenkung [m]

Hierbei ist $F$ die Federkraft, $D$ die Federkonstante und $s$ der Weg der Auslenkung bzw. der Federweg.

Merk’s dir!

Spannt man eine Feder nach unten, so wirkt die Federkraft nach oben. Drückt man eine Feder zusammen, also nach oben, so wirkt die Federkraft nach unten. Das bedeutet also, dass die Federkraft immer genau entgegengesetzt zur Kraft der Auslenkung ist.

Es lässt sich außerdem festhalten: Je länger die Strecke s ist, um die eine Feder gedehnt oder zusammengedrückt wird, desto stärker ist die rückwirkende Federkraft F der Feder.

Federkonstante bzw. Federsteifigkeit

Die Federkonstante D ist abhängig vom Werkstoff und der Bauart der Feder. Mit zunehmender Dicke oder einer engeren Windung des verwendeten Drahtes nimmt die Federkonstante einer Schraubenfeder zu. Sie wird in der Einheit Newton pro Millimeter (N/mm) angegeben und ist der Quotient aus der Federkraft $F$ und dem Federweg $s$ . Durch eine einfache Umstellung der Berechnungsformel der Federkraft lässt sich auch die Federkonstante berechnen:

$D = \dfrac{F}{s}$ Federkonstante

Wir können natürlich ebenfalls den Weg der Auslenkung aus der obigen Gleichung bestimmen, wenn Federkraft und Federkonstante gegeben sind:

$s = \dfrac{F}{D}$ Weg der Auslenkung

Schauen wir uns mal einige Beispiele zur Berechnung von Federkraft, Federkonstante und Federweg an.

1. Beispiel: Kraft berechnen
2. Beispiel: Federkonstante und Kraft berechnen
3. Beispiel: Federweg berechnen

1. Beispiel: Federkraft berechnen

Aufgabenstellung

Es sei eine Schraubenfeder mit der Federkonstante von 1.500 N/m gegeben, die um 250 mm ausgelenkt wird.

Wie groß ist die Kraft mit welcher die Feder ausgelenkt wird?

Die rückwirkende Federkraft und die Kraft der Auslenkung sind gleich groß. Wir können die Federkraft mittels der folgenden Gleichung berechnen:

$F = D \cdot s$

Gegeben haben wir die Federkonstante $D = 1.500 N/M$ und die Länge der Auslenkung $s = 250mm$ .

Zunächst müssen wir die Einheiten in SI-Einheiten umrechnen. Die Federkonstante ist in N/m gegeben, sowohl Newton als auch Meter sind SI-Einheiten. Die Auslenkung ist in Millimeter gegeben, wir müssen diese in Meter umrechnen:

$s = 250 mm = 0,25 m$

Wir setzen die Werte ein:

$F = 1.500 \dfrac{N}{m} \cdot 0,25 m = 375 N$

Die Kraft mit welcher die Feder ausgelenkt wird beträgt 375 N. Federkraft und Kraft der Auslenkung sind gleich groß.

Merk’s dir!

Denk daran, die gegebenen Einheiten falls nötig umzurechnen. Ist Newton N gegeben, so gilt kg m/s². Alle weiteren Einheiten in der Gleichung müssen dann in kg, m oder s angegeben werden. Es ist also nicht möglich in einer Gleichung Newton und z.B. Zentimeter [cm] zu verwenden, da in der Einheit Netwon Meter [m] enthalten ist. Damit du hier keine Schwierigkeiten bekommst, kannst du einfach zunächst alle gegebenen Einheiten in SI-Einheiten umrechnen, sofern diese nicht bereits in SI-Einheiten vorliegen

2. Beispiel: Federkonstante berechnen

Aufgabenstellung

Es sei eine Schraubenfeder gegeben, die mit einer Kraft von $F_G = 250 N$ um eine Länge von 15 cm ausgelenkt wird.

a) Wie groß ist die Federkonstante D?

b) Welche Kraft muss aufgewendet werden um die Feder um eine Länge von 40 cm zu dehnen?

a) Eine Feder wird nach unten mit der Kraft von $F_G = 250 N$ nach unten ausgelenkt. Das bedeutet, dass die rückwirkende Federkraft $F$ ebenfalls 250 N beträgt, denn die Kraft der Ausleknung und die rückwirkende Federkraft sind gleich groß:

$F = F_G = 250 N$

Wir können nun die Federkonstante aus der obigen Gleichung berechnen:

$D = \dfrac{F}{s}$

Gegeben haben wir die Federkraft, denn $F = 250 N$ und die Länge der Auslenkung $s = 15 cm = 0,15m$ .

Wir setzen die Werte ein:

$D = \dfrac{250 N}{0,15 m}$

$D = 1.666,67 \dfrac{N}{m}$

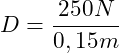
Die Federkonstante beträgt 1666,67 N/m.

b) Wir kennen die Federkonstante $D = 1.666,67 N/m$ und sollen die Kraft der Auslenkung für den Weg von $s = 40 cm$ bestimmen. Die Kraft der Auslenkung und die Federkraft sind gleich groß, weshalb wir die Gleichung für die Berechnung der Federkraft heranziehen können.

$F = D \cdot s$

Zunächst rechnen wir noch in SI-Einheiten um:

$s = 40 cm = 0,4 m$

Wir können als nächstes die Werte einsetzen:

$F = 1.666,67 \frac{N}{m} \cdot 0,4 m = 666,67 N$

Die benötigte Kraft zur Auslenkung der Feder um 0,4m mit der Federkonstante von 1.666,67 N/m beträgt 666,67 N.

3. Beispiel: Federweg berechnen

Aufgabenstellung

Es sei eine Schraubenfeder mit der Federkonstante von 450 N/m gegeben, die mit einer Kraft von $F = 150 N$ zusammengedrückt wird.

Wie groß ist der Federweg bzw. der Weg der Auslenkung?

In diesem Beispiel wollen wir den Weg der Auslenkung bestimmen. Gegeben ist die Federkonstante $D = 450 N/m$ sowie die Kraft $F = 150 N$ . Alle Werte sind in SI-Einheiten gegeben, wir können direkt mit der Berechnung beginnen:

$s = \dfrac{F}{D}$

Einsetzen der gegebenen Werte:

$s = \dfrac{150 N}{450 N/m} = 0,33 m$

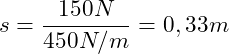
Die Feder mit der Federkonstante von 450 N/m kann mit einer Kraft von 150 N um 0,33 m bzw. 33 cm zusammengedrückt werden. Die Federkraft und die Federkonstante begegnen dir später bei der Berechnung von Schwingungen erneut wieder.

Was kommt als Nächstes?

In der nachfolgenden Lerneinheit zeigen wir dir eine Übersicht über die gängigen Flächenschwerpunkte auf.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++