PH2 – Schiefe Ebene mit zusätzlicher Kraft [Erklärung, Beispiele]

Kräfte an der schiefen Ebene sind die Hangabtriebskraft, die Normalkraft und die Reibungskraft. Diese Kräfte treten infolge der Gewichtskraft der Kiste sowie der Reibung zwischen Kiste und schiefer Ebene auf.

Es kann nun auch eine zusätzliche äußere Kraft an die Kiste angebracht werden, die entweder die Beschleunigung der Kiste erhöht (Kraft in Richtung der Hangabtriebskraft) oder aber der Bewegung entgegenwirkt (Kraft entgegengesetzt zur Hangabtriebskraft).

In dieser Lerneinheit behandeln wir das Thema Schiefe Ebene mit zusätzlicher Kraft.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und zwei anschauliche Rechenbeispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Wir behandeln in diesem Text wieder einen Körper auf der schiefen Ebene. Dieses mal greift aber eine zusätzlich Kraft an. Eine solche Kraft könnte die Kiste zum Beispiel die Ebene hinab oder die Ebene hinauf ziehen.

Betrachten wir hierzu ein Beispiel.

Beispiel!

Schiefe Ebene mit Kraft — Schiefe Ebene mit zusätzlicher Kraft

In dem obigen Beispiel greift eine zusätzliche Kraft F = 45 N an die Kiste an. Der Haftungskoeffizient betrage μ₀ = 0,5. Der Winkel zwischen der Waagerechten und der schiefen Ebene beträgt α= 18°. Die Masse der Kiste betrage m = 50 kg.

Rutscht die Kiste ohne Kraft F?

Schiefe Ebene ohne zusätzliche Kraft

Schiefe Ebene, Kräfte, Hangabtriebskraft, Reibungskraft, Normalkraft — Schiefe Ebene ohne zusätzliche Kraft: Hangabtriebskraft, Normalkraft, Reibungskraft

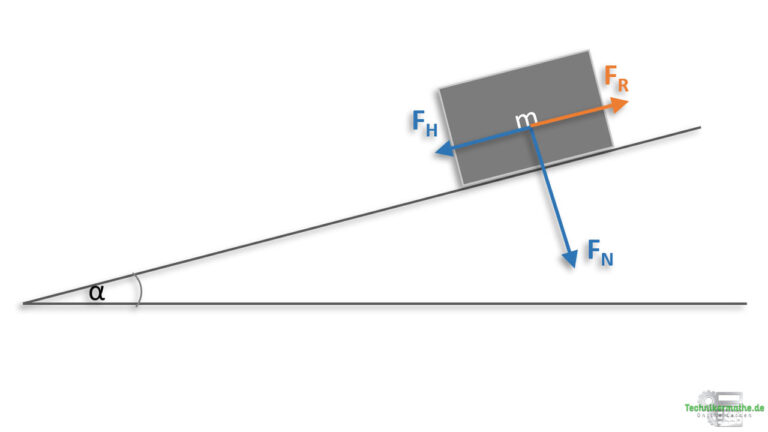
Infolge der Gewichtskraft der Kiste tritt die Hangabtriebskraft $F_H$ sowie die Normalkraft $F_N$ auf. Die Reibungskraft $F_R$ entsteht infolge der Reibung zwischen der Kiste und der schiefen Ebene und wirkt immer entgegengesetzt zur möglichen Bewegung.

Ob die Kiste rutscht oder nicht können wir ohne zusätzlichen Kraftangriff über den Haftungswinkel $\alpha_0$ bestimmen. Das ist der Winkel, bei welchem die Kiste gerade noch auf der schiefen Ebene haftet. Ist der Haftungswinkel gegeben, so ist die Hangabtriebskraft $F_H$ gleich der Reibungskraft $F_R$ .

Wir berechnen den Haftungswinkel $\alpha_0$ aus der folgenden Gleichung:

$\tan(\alpha_0) = \mu_0$

$\alpha_0 = \tan^{-1} (\mu_0)$

$\alpha_0=\tan^{-1} (0,5) = 26,57^\circ$

Ohne die zusätzliche Kraft F haftet die Kiste bis zu einem Neigungswinkel von 26,57° auf der schiefen Ebene. Ist der Neigungswinkel größer als 26,57°, so beginnt die Kiste zu rutschen. In diesem Beispiel haftet die Kiste, weil der gegebene Winkel von 18° kleiner als der Haftungswinkel $\alpha_0$ ist.

Schiefe Ebene mit zusätzlicher Kraft

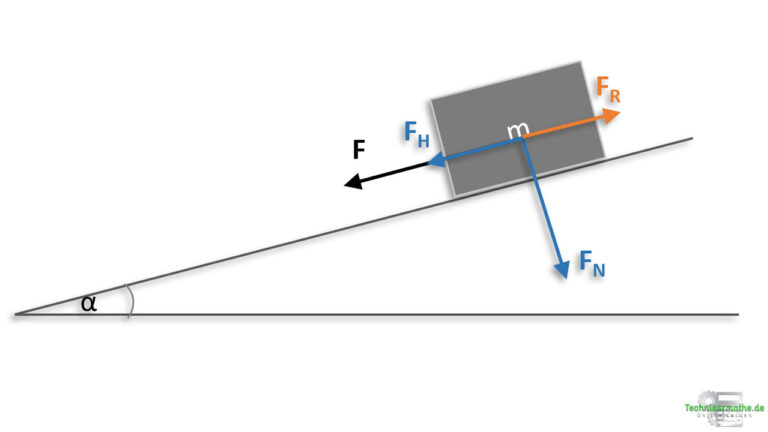
Die Kraft F zieht die Kiste nach unten. Demnach ist hier, neben der Hangabtriebskraft $F_H$ , eine zusätzliche Kraft gegeben, welche die Kiste die schiefe Ebene nach unten befördern möchte. Wir wollen nun herausfinden, ob sich die Kiste auch unter Berücksichtigung von der Kraft F im Gleichgewicht befindet, also nicht rutscht.

Wir können die Berechnung hier nicht über den Haftungswinkel $\alpha_0$ durchführen, sondern müssen uns die Kräfte parallel zur schiefen Ebene anschauen. Dazu bilden wir die Summe der Kräfte, die parallel zur schiefen Ebene liegen. Wir wählen die Kräfte nach links unten (in Richtung der Bewegung) positiv und die Kräfte nach rechts oben negativ:

I. $F_H + F - F_R = 0$

Alle positiven Kräfte ( $F_H$ und $F$ ) führen dazu, dass sich die Kiste nach unten bewegt. Alle negativen Kräfte ( $F_R$ ) führen dazu, dass die Kiste dem rutschen entgegenwirkt. Da keine Bewegung stattfinden soll, muss die Summe der Kräfte gleich Null ergeben.

Wir berechnen nun die Hangabtriebskraft F_H und die Reibungskraft F_R.

$F_H = m \cdot g \cdot \sin(\alpha) = 50 kg \cdot 9,81 \frac{m}{s^2} \cdot \sin(18^\circ) = 151,57 N$

$F_R = \mu_0 \cdot F_N$

Wir benötigen zunächst die Kraft F_N:

$F_N = m \cdot g \cdot \cos(\alpha) = 50 kg \cdot 9,81 \frac{m}{s^2} \cdot \cos(18^\circ) =466,49 N$

$F_R = 0,5 \cdot 466,49 N = 233,25 N$

Einsetzen in die Gleichung I:

I. $F_H + F - F_R = 0$

I. $151,57 N + 45 N - 233,25 N = -63,68 N$

Die Summe aller Kräfte ergibt eine negative Kraft. Wir haben festgelegt, dass die negativen Kräfte nach rechts oben zeigen. Das bedeutet also, dass die Reibungskraft größer ist, als die Hangabtriebskraft $F_H$ und die Kraft $F$ zusammen. Demnach haftet die Kiste auf der schiefen Ebene und rutscht trotz zusätzlicher Kraft $F$ nicht die schiefe Ebene herunter.

Greift eine zusätzliche Kraft in Richtung der Hangabtriebskraft an, so führt dies zu einer größeren resultierenden Kraft. Damit die Kiste jetzt nicht rutscht, muss die Reibungskraft $F_R$ größer sein, als die Summe aus der zusätzlichen Kraft $F$ und der Hangabtriebskraft $F_H$ :

$F_R > F_H + F$ Kiste haftet

$F_R < F_H + F$ Kiste rutscht

Wir wollen nun zwei Kräfte betrachten, die dazu führen sollen einen Körper auf der schiefen Ebene nach oben bzw. nach unten zu bewegen.

Wir haben also gezeigt, dass eine zusätzliche Kraft eine Auswirkung auf die Kiste haben kann, aber nicht haben muss. Wir wollen uns im Folgenden anschauen, wie sich die Bewegung ergibt, wenn eine Abwärtskraft und eine Aufwärtskraft zusätzlich gegeben sind.

Schiefe Ebene mit Aufwärtskraft

Betrachten wir als erstes die Aufwärtskraft $F_{auf}$ , die nötig ist, um die Kiste nach rechts oben zu bewegen.

Aufwärtskraft, schiefe Ebene, Normalkraft, Reibungskraft, Hangabtriebskraft — Schiefe Ebene mit Aufwärtskraft

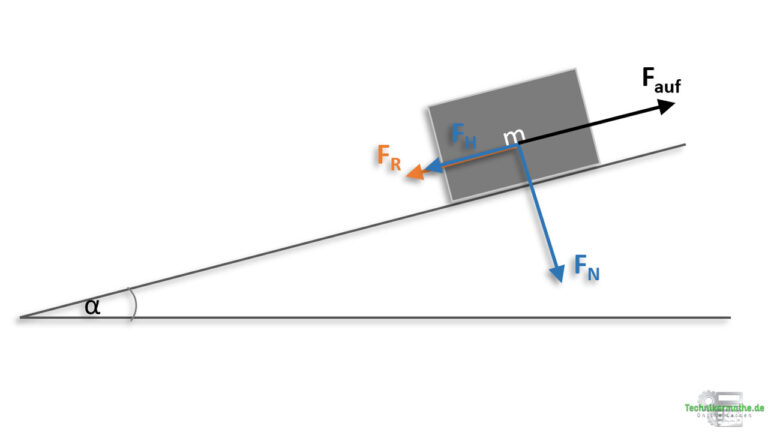
Wir wollen die Größe der Kraft $F_{auf}$ berechnen, die notwendig ist damit sich die Kiste nach oben bewegt. Die Bewegung wird jetzt also nach rechts oben angenommen. Da die Reibungskraft $F_R$ immer entgegengesetzt zur Bewegung wirkt, müssen wir diese nun nach links unten einzeichnen.

Wir berechnen zunächst wieder den Grenzfall, also bis wann gerade noch Haftung besteht und die Kiste sich nicht bewegt. Dazu bilden wir wieder die Summe der Kräfte für alle zur schiefen Ebene parallelen Kräfte. In diesem Fall gehen wir aber davon aus, dass die Kiste sich nach oben bewegt. Deswegen wählen wir die Kräfte die nach rechts oben zeigen positiv und die Kräfte die nach links unten zeigen negativ (Kräfte in Richtung der möglichen Bewegung werden also positiv berücksichtigt):

I. $-F_H - F_R + F_{auf} = 0$

Auflösen nach der gesuchten Aufwärtskraft:

$F_{auf} = F_H + F_R$

Da sich an der Aufgabenstellung nichts geändert hat, können wir die Hangabtriebskraft $F_H$ und die Reibungskraft $F_R$ von oben übernehmen:

$F_{auf} = 151,57 N + 233,25 N$

$F_{auf} = 384,82 N$

Greift eine Kraft bis 384,82 N an, so bewegt sich die Kiste nicht. Eine Kraft größer als 384,82 N hingegen führt dazu, dass sich die Kiste nach rechts oben bewegt.

Schiefe Ebene mit Abwärtskraft

Betrachten wir als nächstes die Abwärtskraft $F_{ab}$ , die nötig ist, um die Kiste nach links unten zu bewegen. Das haben wir bereits im ersten Beispiel berechnet. Dieses mal haben wir die Abwärtskraft aber nicht vorgegeben, sondern sollen die Größe der Abwärtskraft berechnen, die notwendig ist, damit sich die Kiste nach unten bewegt. Dies ist dann der Fall, wenn Hangabtriebskraft $F_H$ und Abwärtskraft $F_{ab}$ die Reibungskraft $F_R$ überwinden.

Abwärtskraft, schiefe Ebene, Reibungskraft, Normalkraft — Schiefe Ebene mit Abwärtskraft

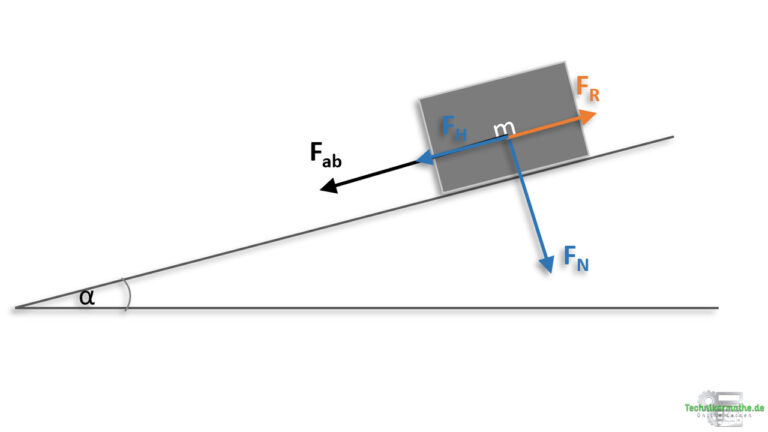
Die Bewegung nehmen wir jetzt nach links unten an. Die Reibungskraft $F_R$ wirkt immer entgegengesetzt zur Bewegung, in diesem Fall also nach rechts oben.

Wir berechnen zunächst wieder den Grenzfall, also bis wann noch gerade Haftung besteht und die Kiste sich nicht nach links unten bewegt. Dazu bilden wir wieder die Summe der Kräfte, die parallel zur schiefen Ebene liegen. Da die Bewegung nun nach links unten angenommen wird, berücksichtigen wir alle Kräfte die nach links unten zeigen positiv:

I. $F_H + F_{ab} - F_R = 0$

Auflösen nach der gesuchten Abwärtskraft ergibt dann:

$F_{ab} = F_R - F_H$

Einsetzen von $F_H = 151,57 N$ und $F_R = 233,25 N$ :

$F_{ab} = 233,25 N - 151,57 N$

$F_{auf} = 81,68 N$

Greift eine Kraft bis 81,68 N an, so bewegt sich die Kiste nicht. Eine Kraft größer als 81,68 N hingegen führt dazu, dass sich die Kiste in Bewegung setzt (nach links unten).

Sollst du die Größe der Auftriebskraft bzw. Abtriebskraft berechnen, so kannst du die folgenden Gleichungen verwenden:

$F_{auf} = F_H - F_R$

$F_{ab} = F_H + F_R$

Was kommt als Nächstes?

Nachdem wir jetzt die Schiefe Ebene mit zusätzlicher Kraft berechnet haben, betrachten wir im nächsten Kurstext eine weitere für dich relevante Kraft, die Federkraft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++