Wir wollen in dieser Lerneinheit anhand eines Beispiel zeigen, wie du die Lagerkräfte berechnen kannst.
Die Berechnung von Lagerkräfte erfolgt aus den Gleichgewichtsbedingungen. Dazu wird zunächst das betrachtete Bauteil von den Auflagern freigeschnitten und die Auflagerreaktionen abgetragen. Danach erfolgt eine Kräftezerlegung für alle äußeren Kräfte, die einen Winkel aufweisen. Im letzten Schritt werden die unbekannten Lagerkräfte aus den Gleichgewichtsbedingungen berechnet.
Für ein optimales Verständnis helfen dir drei Videoclips und ein ausführliches Beispiel zu dem Thema.
Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.
Vorgehensweise: Berechnung von Lagerkräften
Hierzu wenden wir die Gleichgewichtsbedingung in x-Richtung und y-Richtung sowie die Momentengleichgewichtsbedingung an. Die nachfolgende Vorgehensweise soll ich dir helfen, einen routinierten Ablauf zu erhalten, so dass du innerhalb der Prüfung keine Zeit verlierst.
![PH2 - Prüfungsaufgabe: Berechnung der Lagerkräfte [Erklärung, Beispiel, Videos] 1 Vorgehensweise zur Berechnung von Lagerkräften](https://technikermathe.de/wp-content/uploads/2020/03/vorgehensweise-berechnung-von-lagerkraeften.jpg)
1.Schritt: Freischnitt
Zunächst musst du den betrachteten Körper/das Tragwerk von seiner Umgebung freischneiden. Damit trennst du das Tragwerk von seinen Auflagern und trägst dann die Lagerkräfte ab. Dazu solltest du wissen, welche Auflager gegeben sind und welche Kräfte die jeweiligen Auflager übertragen.
- Ein Festlager überträgt zum Beispiel eine vertikale und eine horizontale Kraft.
- Ein Loslager überträgt eine vertikale oder horizontale Kraft (je nachdem wie es angebracht ist).
- Eine feste Einspannung überträgt eine vertikale und eine horizontale Kraft sowie ein Moment.
![PH2 - Prüfungsaufgabe: Berechnung der Lagerkräfte [Erklärung, Beispiel, Videos] 2 Berechnung von Lagerkräften: Übersicht über die Lagerarten](https://technikermathe.de/wp-content/uploads/2020/03/tk-physik-lagerarten-uebersicht.jpg)
2.Schritt: Kräftezerlegung
Für jede Kraft, die einen Winkel aufweist, musst du zunächst eine Kräftezerlegung durchführen. Dazu bestimmst du für die gegebene Kraft den Winkel zur Horizontalen (falls nicht gegeben). Danach legst du die Kraft mit dem Anfangspunkt in ein Koordinatensystem und berechnest mittels Kosinus die x-Komponente und mittels Sinus die y-Komponente. Je nachdem in welche Richtung bzw. in welchem Quadranten die Ausgangskraft liegt, können die Kraftkomponenten in positive oder negative Achsenrichtung zeigen.
Ist der Winkel von einer schrägen Kraft F zur Horizontalen gegeben, dann kannst du die Kräftezerlegung wie folgt durchführen:
Komponente in x-Richtung
Komponente in y-Richtung
Du ersetzt nun die Kraft mit Winkel durch die beiden Kraftkomponenten und
.
3.Schritt: Gleichgewichtsbedingungen anwenden
Nachdem du das Tragwerk von den Auflagern frei geschnitten hast und die Kraft/Kräfte (sofern vorhanden) in zwei Komponenten zerlegt hast, kannst du mit der Berechnung der unbekannten Lagerkräfte starten.
- Alle horizontalen Kräfte gehen in die Gleichgewichtsbedingung in x-Richtung ein. Hierbei berücksichtigst du alle Kräfte die nach rechts zeigen positiv und alle Kräfte die nach nach links zeigen negativ.
- Alle vertikalen Kräfte gehen in die Gleichgewichtsbedingungen in y-Richtung ein. Hierbei berücksichtigst du alle Kräfte die nach oben zeigen positiv und alle Kräfte die nach nach unten zeigen negativ.
- Für die Momente gilt, dass diese in der Momentengleichgewichtsbedingung erfasst werden. Alle linksdrehenden Momente sind positiv, alle rechtsdrehenden Momente negativ zu berücksichtigen.
Videoclips: Lagerkräfte bestimmen
In den folgenden beiden Videoreihen zeige ich dir, wie du unbekannte Lagerkräfte unter Anwendung der drei Gleichgewichtsbedingungen bestimmen kannst.
Schauen wir uns mal eine Aufgabe zur Berechnung von Lagerkräften aus den drei Gleichgewichtsbedingungen an.
Aufgabe: Lagerkräfte berechnen
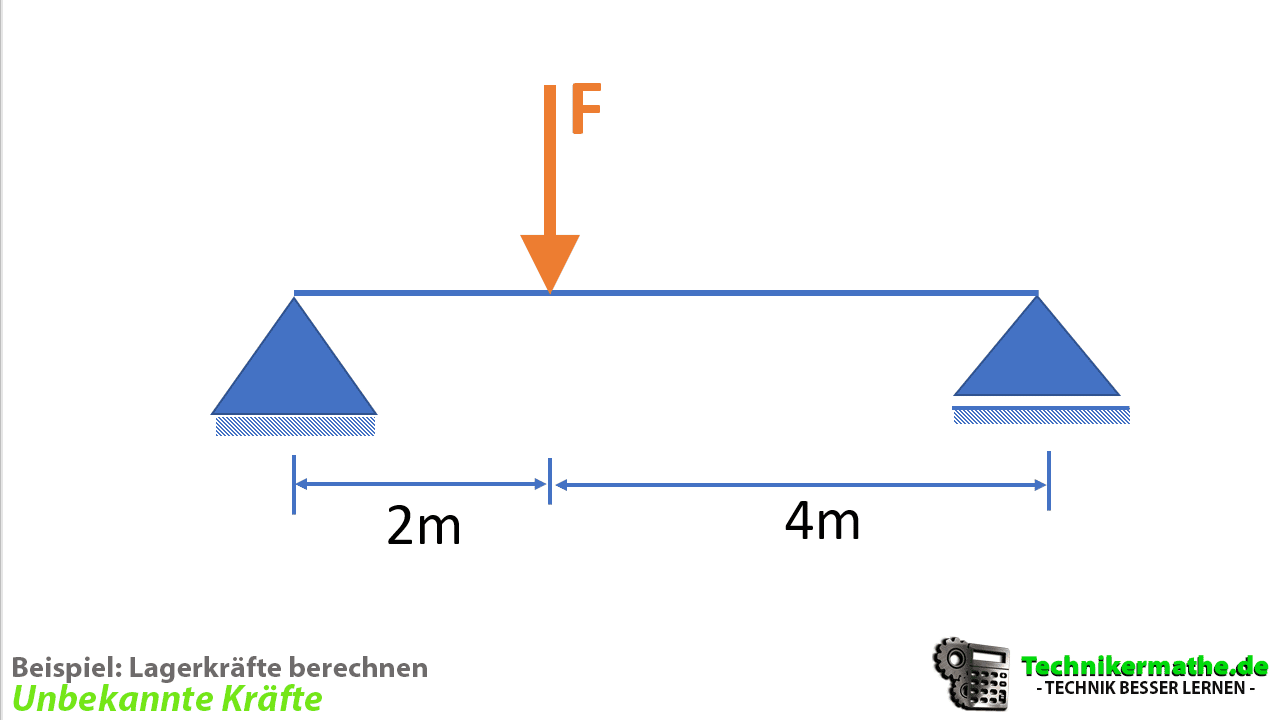
Gegeben sei der obige Balken, auf welchen eine vertikale Kraft mit 200 N wirkt. Der Balken ist auf einem Festlager (links) und einem Loslager (rechts) gelagert.
Bestimme alle Auflagerkräfte!
Schritt 1 – Freischnitt
Bevor wir die Lagerkräfte berechnen, müssen wir den Balken von den Auflagern freischneiden, d.h. wir tragen stattdessen die Auflagerkräfte an. Ein Festlager überträgt zwei Kräfte (vertikal und horizontal zur Unterlage) und ein Loslager eine Kraft vertikal zur Unterlage.
![PH2 - Prüfungsaufgabe: Berechnung der Lagerkräfte [Erklärung, Beispiel, Videos] 4 Lagerkräfte berechnen, Freischnitt](https://technikermathe.de/wp-content/uploads/2020/03/tk-statik-beispiel1-lagerkraefte-2-768x432.jpg)
Wir bezeichnen das linke Lager mit A und geben die Lagerkräfte jeweils mit (horizontale Lagerkraft) und
(vertikale Lagerkraft) an. Das rechte Lager bezeichnen wir als B mit der vertikalen Lagerkraft
.
Schritt: 2 – Kräftezerlegung
Da keine Kraft mit Winkel gegeben ist, muss hier auch keine Kräftezerlegung durchgeführt werden.
Schritt 3 – Gleichgewichtsbedingungen aufstellen
Wir können nun damit beginnen die Lagerkräfte zu berechnen, indem wir die drei Gleichgewichtsbedingungen in der Ebene anwenden:
I. Gleichgewichtsbedingung in x-Richtung
II. Gleichgewichtsbedingung in y-Richtung
III. Momentengleichgewichtsbedingung
![PH2 - Prüfungsaufgabe: Berechnung der Lagerkräfte [Erklärung, Beispiel, Videos] 5 Beispiel 1: Freischnitt](https://technikermathe.de/wp-content/uploads/2020/03/tk-statik-beispiel1-lagerkraefte-2-768x432.jpg)
Gleichgewichtsbedingung in x-Richtung
Wir beginnen mit der Gleichgewichtsbedingung in x-Richtung. Alle Kräfte die in x-Richtung zeigen werden hier berücksichtigt. Kräfte in negative x-Richtung werden mit einem Minuszeichen versehen:
I.
Es wirken keine äußeren horizontalen Kräfte auf den Balken. Demnach tritt auch keine horizontale Lagerkraft auf.
Gleichgewichtsbedingung in y-Richtung
Als nächstes betrachten wir die Gleichgewichtsbedingung in y-Richtung. Alle Kräfte die in y-Richtung zeigen werden hier berücksichtigt. Kräfte in negative y-Richtung werden mit einem Minuszeichen versehen:
II.
Die Kraft F wird negativ berücksichtigt, weil diese nach unten in negative y-Richtung zeigt. Wir können hier noch keine Lagerkraft berechnen, da wir zwei unbekannte Lagerkräfte und
gegeben haben.
Momentengleichgewichtsbedingung
Bei der Anwendung der Momentengleichgewichtsbedingung müssen wir zunächst einen geeigneten Bezugspunkt festlegen. Bei der Berechnung von Auflagerkräften legt man den Bezugspunkt dort hin, wo die meisten unbekannten Kräfte gegeben sind. Bis jetzt sind die Auflagerkräfte und
unbekannt, weshalb wir den Bezugspunkt entweder in das Lager B oder in das Lager A legen können. Wir legen den Bezugspunkt in das Lager A. [/intense_content_box]
Schauen wir uns nochmal den Freischnitt an:
![PH2 - Prüfungsaufgabe: Berechnung der Lagerkräfte [Erklärung, Beispiel, Videos] 5 Beispiel 1: Freischnitt](https://technikermathe.de/wp-content/uploads/2020/03/tk-statik-beispiel1-lagerkraefte-2-768x432.jpg)
Wir berechnen nun alle Momente auf den Bezugspunkt im Lager A und erhalten:
III.
fällt aus der Berechnung raus, da die Wirkungslinie den Bezugspunkt schneidet, dasselbe gilt für
. Die Kraft
weist den senkrechten Abstand von 2m auf, die Kraft
den Abstand von 6m. Es stellt sich nur noch die Frage, welches davon ein rechts- und welches ein linksdrehendes Moment darstellt.
Dazu stellt man sich den Balken im Bezugspunkt fixiert vor. Wir starten mit der Kraft und der Drehwirkung dieser Kraft auf den gewählten Bezugspunkt. Die Kraft
drückt den Balken nach unten, es würde sich dann eine Drehung im Uhrzeigersinn ergeben (rechtsdrehendes Moment = negativ).
Danach betrachten wir die Lagerkraft und die Drehwirkung auf den gewählten Bezugspunkt. Die Lagerkraft
drückt den Balken nach oben und es ergibt sich eine Drehung gegen den Uhrzeigersinn (linksdrehendes Moment = positiv).
Da die äußere Kraft gegeben ist, können wir aus der III. Gleichung die Auflagerkraft
berechnen:
Aus III)
Dazu lösen wir die Gleichung nach auf:
|
|
Einsetzen der gegebenen Werte:
Da wir nun die Auflagerkraft gegeben haben, können wir aus der II. Gleichung
berechnen:
Aus II)
Auflösen nach :
Einsetzen der gegebenen Werte:
Damit sich der Balken im Gleichgewicht befindet, sich also infolge der Kraft nicht in y-Richtung bewegt bzw. in der x,y-Ebene rotiert, muss das Lager B eine Lagerkraft von
und das Lager A eine Lagerkraft von
aufbringen. Da keine horizontalen Kräfte auf den Balken wirken, wird die Auflagerkraft
.
In der nachfolgenden Lerneinheit schauen wir uns eine weitere klausurrelevante Aufgabe an, in welcher wir Lagerkräfte berechnen und zusätzlich eine Kräftezerlegung durchführen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.


Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team






