PH2 – Gleichgewichtsbedingungen [Erklärung, Beispiele, Videos]

Wir betrachten in dieser Lerneinheit die Gleichgewichtsbedingungen in der Ebene. Diese dienen dazu unbekannte Kräfte, wie z.B. Lagerkräfte, Seilkräfte, Stabkräfte oder Schnittgrößen zu berechnen. Wir befinden uns innerhalb der Statik und betrachten damit ruhende Körper.

Die Summe aller auf den betrachteten Körper wirkenden Kräfte müssen sich im Gleichgewicht befinden, damit dieser ruht. Das bedeutet, dass die Summe aller Kräfte Null ergeben muss.

In dieser Lerneinheit betrachten wir die Gleichgewichtsbedingungen zur Berechnung von unbekannten Kräften und ein Beispiel zur Berechnung von unbekannten Lagerkräften.

Für ein optimales Verständnis helfen dir drei ausführliche Videoclips und ein anschauliche Rechenbeispiele (Lagerkräfte berechnen) zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Merk’s dir!

Wir beginnen in dieser und den folgenden Lerneinheiten mit der Berechnung der unbekannten Lagerkräfte aus den Gleichgewichtsbedingungen. Du solltest dafür die folgenden Themen aus unseren Lerneinheiten bereits kennen:

Trigonometrie am rechtwinkligen Dreieck
Lagerarten und Lagerkräfte
Kräftezerlegung
Elemente eines Tragwerks

Relevant ist vor allem die Kräftezerlegung, welche du immer dann durchführen musst, wenn eine Kraft in der Ebene wirkt, d.h. eine Kraft mit Winkel gegeben sind.

Gleichgewichtsbedingungen in der Ebene

Du benötigst die Gleichgewichtsbedingungen zum Beispiel um unbekannte Lagerkräfte oder die Schnittgrößen zu berechnen. In der Ebene existieren drei Gleichgewichtsbedingungen:

Gleichgewichtsbedingung in x-Richtung
Gleichgewichtsbedingung in y-Richtung
Momentengleichgewichtsbedingung

Die ersten beiden Gleichgewichtsbedingungen sagen nichts anderes aus, als dass die Summe aller Kräfte in x- und y-Richtung gleich Null (=0) sein muss, damit keine Bewegung in x- und y-Richtung stattfindet. Denn innerhalb der Statik betrachten wir ruhende Körper, weshalb keine Bewegungen auftreten dürfen.

Die Momentengleichgewichtsbedingung sagt aus, dass keine Rotation (Drehung) des betrachteten Körpers in der x,y-Ebene stattfindet. Dafür muss die Summe aller Momente auf einen beliebigen Bezugspunkt gleich Null (=0) sein. Die Summe aller Momente auf einen bestimmten Punkt darf also keine Drehwirkung des Körpers ergeben.

Schauen wir uns mal die drei Gleichgewichtsbedingungen in Formeldarstellung an.

Gleichgewichtsbedingungen – Formeln

Gleichgewichtsbedingung in x-Richtung:

$\sum F_x = 0$

Innerhalb der Gleichgewichtsbedingung in x-Richtung berücksichtigen wir nur horizontale Kräfte. Alle Kräfte die nach rechts zeigen (in positive x-Richtung) sind positiv zu berücksichtigen und alle Kräfte die nach links zeigen somit negativ.

Gleichgewichtsbedingung in y-Richtung:

$\sum F_y = 0$

Innerhalb der Gleichgewichtsbedingung in y-Richtung berücksichtigen wir nur vertikale Kräfte. Hier gilt, dass alle Kräfte die nach oben zeigen (in positive y-Richtung) positiv und somit alle Kräfte die nach unten zeigen negativ zu berücksichtigen sind.

Momentengleichgewichtsbedingung:

$\sum M = 0$

Innerhalb der Momentengleichgewichtsbedingung betrachten wir alle Momente auf einen vorher festgelegten Bezugspunkt. Dabei sind linksdrehende Momente (gegen den Uhrzeigersinn) positiv zu berücksichtigt und rechtsdrehende Momente (mit dem Uhrzeigersinn) negativ.

Videos: Gleichgewichtsbedingungen

In den folgenden Videos zeige ich dir, wie du die drei Gleichgewichtsbedingungen anwendest.

Beispiel: Lagerkräfte berechnen

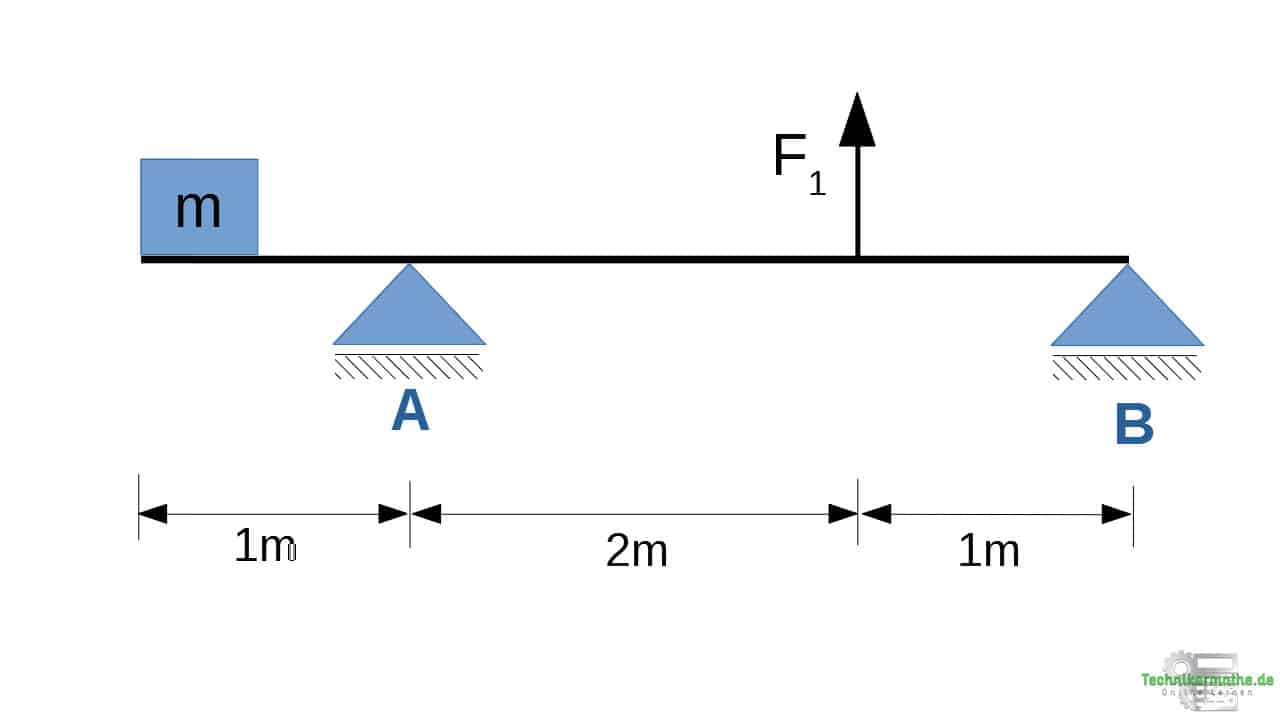
Schau dir die Aufgabenstellung genau an und löse die Aufgabe. Wende dabei die folgenden drei Schritte an:

Vorgehensweise: Lagerkräfte bestimmen

Freischnitt
Kräftezerlegung durchführen
Gleichgewichtsbedingungen aufstellen

Aufgabenstellung

Gleichgewichtsbedingungen, Lagerkräfte bestimmen, Lagerkräfte berechnen — Beispiel: Lagerkräfte berechnen

Ein Balkenträger mit zwei Auflagepunkten (A und B) wird mit einer Masse von m = 50 kg und einer Zugkraft F₁ = 200 N belastet (siehe Skizze). Die Gewichtskraft des Trägers wird vernachlässigt. (Hinweis: g = 9,81 m/s²)

Berechne die Lagerkräfte!

Schritt 1: Freischnitt

Bevor wir Lagerkräfte bestimmen können, müssen wir den Balken zum Einen von seinen Auflagern freischneiden und zum anderen das Gewicht mit der Masse $m$ durch die Gewichtskraft ersetzen. Es gilt:

$F_G = m \cdot g$

Einsetzen der gegebenen Werte:

$F_G = 50 kg \cdot 9,81 \frac{m}{s^2} = 490,5 N$

Die Gewichtskraft liegt immer im Schwerpunkt des betrachteten Körpers und zeigt immer vertikal nach unten. In diesem Fall ist de Körper ein Quadrat/Rechteck. Der Schwerpunkt liegt in der Mitte, demnach greift die Gewichtskraft genau in der Mitte an und zeigt vertikal nach unten:

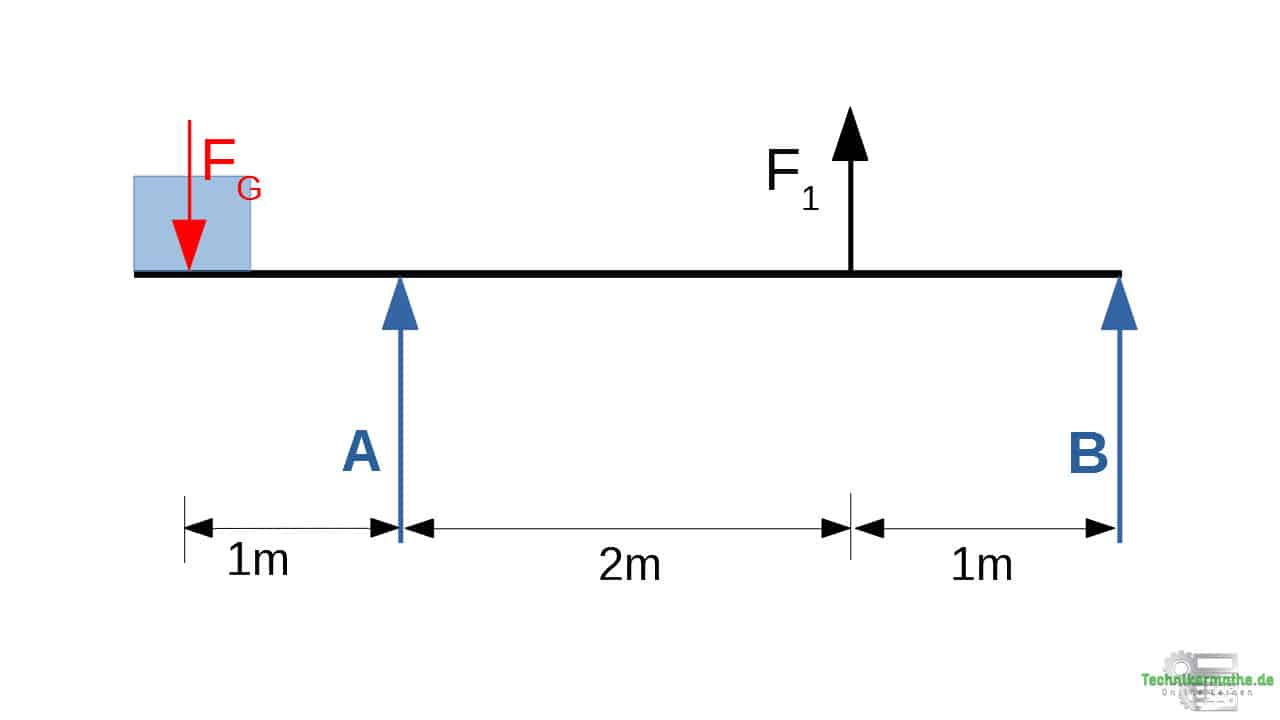
Lagerkräfte berechnen, Gleichgewichtsbedíngungen — Freischnitt

Schritt 2: Kräftezerlegung

Es ist keine Kraft mit Winkel gegeben.

Schritt 3: Gleichgewichtsbedingungen

Wir wollen als nächstes mittels der drei Gleichgewichtsbedingungen in der Ebene die Lagerkräfte bestimmen:

I. $\sum F_x = 0$ Gleichgewichtsbedingung in x-Richtung

II. $\sum F_y = 0$ Gleichgewichtsbedingung in y-Richtung

III. $\sum M^{X} = 0$ Momentengleichgewichtsbedingung

Gleichgewichtsbedingung in x-Richtung

Wir stellen zunächst die Gleichgewichtsbedingung in x-Richtung auf und berücksichtigen alle horizontalen Kräfte. Alle nach rechts gerichteten Kräfte gehen positiv, alle nach links gerichteten Kräfte negativ in die Gleichgewichtsbedingungen ein.

I. $\sum F_x = 0$ :

Es existieren keine horizontalen Kräfte.

Gleichgewichtsbedingung in y-Richtung

Als nächstes betrachten wir die Gleichgewichtsbedingung in y-Richtung und berücksichtigen alle vertikalen Kräfte. Alle nach oben gerichteten Kräfte gehen positiv, alle nach unten gerichteten Kräfte negativ in die Gleichgewichtsbedingungen ein.

II. $\sum F_y = 0$ :

II. $A + B - F_G + F_1 = 0$

Bereits aus der Aufgabenstellung gegeben sind $F_G$ und $F_1$ . Unbekannt sind die beiden Auflagerkräfte $A$ und $B$ . Wir benötigen die Momentengleichgewichtsbedingung, zur Berechnung einer der Kräfte.

Momentengleichgewichtsbedingung aufstellen

Wir legen den Bezugspunkt dorthin, wo eine unbekannte Kraft gegeben ist. Also entweder in $A$ oder in $B$ (beide sind noch unbekannt). Wir wählen beliebig das Lager A.

Wir müssen nun alle Momenten auf diesen Bezugspunkt berechnen. Solltest du dir unsicher sein wie das genau funktioniert, schau dir nochmal das folgende Video an.

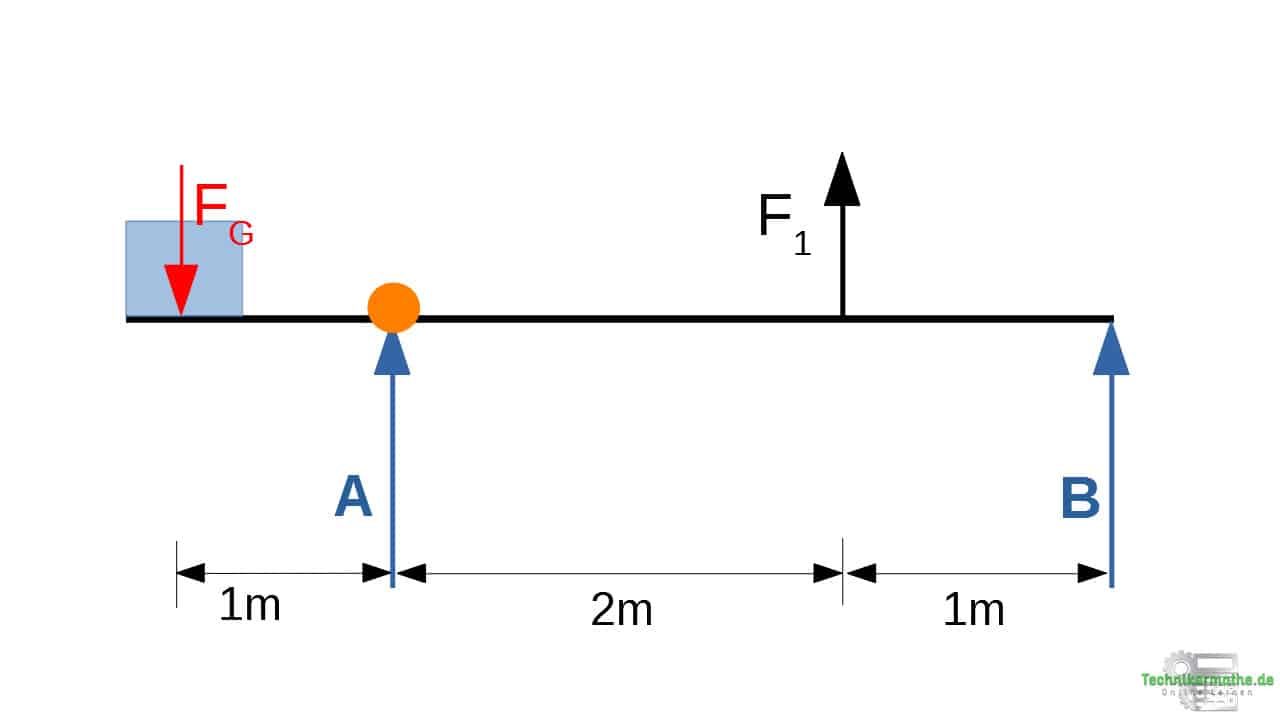
Lagerkräfte, Momentengleichgewichtsbedingung, Beispiel, Bezugspunkt — Momentengleichgewichtsbedingung aufstellen

III. $\sum M^A = 0$ :

$F_G \cdot 1m + F_1 \cdot 2m + B \cdot 3m = 0$

Alle Momente sind positiv, denn sie drehen den Balken in einer Linksdrehung (gegen den Uhrzeigersinn) um den gewählten Bezugspunkt. Wir lösen die Gleichung nach $B$ auf:

$B \cdot 3m = - F_G \cdot 1m - F_1 \cdot 2m$

$B = \frac{-F_G \cdot 1m - F_1 \cdot 2m}{3m}$

Werte einsetzen:

$B = \frac{-490,5 N \cdot 1m - 200 N \cdot 2m}{3m} = -296,83 N$

Die Lagerkraft ist negativ. Was bedeutet das?

Die Lagerkraft B zeigt nicht – wie angenommen – nach oben, sondern genau entgegengesetzt (um 180°) gedreht nach unten, in negative y-Richtung.

Merk’s dir!

Beim Freischneiden müsst ihr nur wissen, auf welcher Wirkungslinie die Lagerkräfte liegen (z.B. auf einer Vertikalen). In welche Richtung diese zeigen (z.B. nach oben oder unten) ist zunächst nicht relevant. Ihr könnt euch also für eine Möglichkeit entscheiden. Das Ergebnis zeigt euch dann an, ob die gewählte Richtung stimmt (positive Kraft) oder die Kraft genau in entgegengesetzte Richtung zeigt (negative Kraft).

In diesem Beispiel ist die Lagerkraft B eine Kraft die vertikal gerichtet ist. Ob diese nun aber nach oben oder nach unten wirkt, das ist nicht immer sofort erkennbar. Demnach wählst du eine Richtung (nach oben oder nach unten) beliebig aus. Das Ergebnis hier zeigt dir, dass die gewählte Richtung nicht stimmt. Die Lagerkraft B wirkt tatsächlich nach unten und nicht nach oben.

Als nächstes berechnen wir aus der Gleichgewichtsbedingung in y-Richtung die Lagerkraft A.

Aus II. )

II. $A + B - F_G - F_1 = 0$

Einsetzen aller bekannten Kräfte:

$A + (-296,33 N) - 490,5 N + 200 N = 0$

Auflösen nach $A$ :

$A = 296,33 N + 490,5 N - 200 N = 586,83 N$

Damit sich der Balken im Gleichgewicht befindet, sich also infolge der Kraft $F_1$ und der Gewichtskraft $F_G$ nicht in y-Richtung bewegt bzw. in der x,y-Ebene rotiert, muss das Lager B eine Lagerkraft von $B = 296,83 N$ aufnehmen und ist nach unten gerichtet. Das Lager muss eine Lagerkraft von $A = 586,83 N$ aufbringen und ist nach oben gerichtet.

Was kommt als Nächstes?

In der nachfolgenden Lerneinheit schauen wir uns eine weitere klausurrelevante Aufgabe an, in welcher wir Lagerkräfte bestimmen und zusätzlich eine Kräftezerlegung durchführen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++