Ein Drehmoment ist eine Kraft, die bewirkt, dass sich ein Objekt um einen bestimmten Punkt dreht oder eine Drehung erfährt. Stell dir vor, du nutzt einen Schraubenschlüssel, um eine Mutter festzuziehen. Wenn du am Griff des Schraubenschlüssels drehst, erzeugst du ein Drehmoment, das die Mutter dazu bringt, sich um die Schraube zu drehen.
In der Physik wird das Drehmoment mathematisch als das Produkt aus der angewandten Kraft und dem senkrechten Abstand von dem Drehpunkt definiert. Es wird in Newtonmetern (Nm) gemessen.
Drehmomente sind wichtig in vielen Bereichen wie Mechanik, Maschinenbau und Physik, da sie helfen, die Bewegung von Objekten zu verstehen und zu kontrollieren.
Für ein optimales Verständnis helfen dir ein zwei Videoclips und ein anschauliches Rechenbeispiel zu dem Thema.
Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.
Drehmoment – Grundlagen
Ist ein zentrales Kräftesystem gegeben, in welchem sich alle Kräfte in einem einzigen Punkt schneiden, so treten keine Drehmomente auf. In einem allgemeinen Kräftesystem hingegen, wo sich die Kräfte nicht allein einem Punkt schneiden, treten zusätzliche Drehmomente auf.
Ein Drehmoment M entsteht durch eine Kraft F, die über einen Hebelarm h auf einen bestimmten Punkt wirkt.
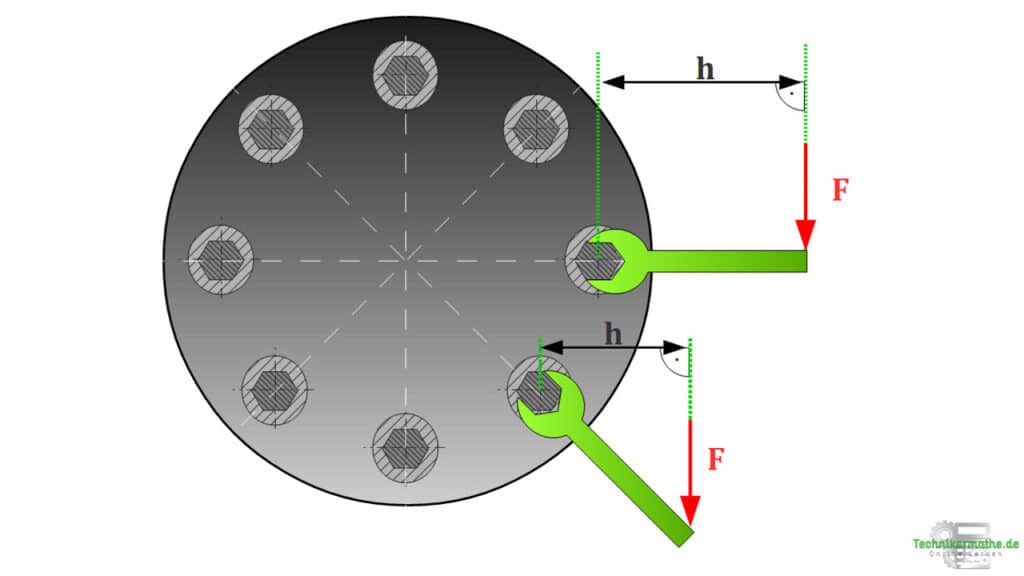
In der obigen Grafik wirken die beiden Kräfte 
auf das Ende des Maulschlüssels. Wir betrachten als gewählten Bezugspunkt die Schraube. Wird nun der Maulschlüssel mit der Kraft belastet und damit nach unten gedrückt, so dreht sich die Schraube. Es ist also ein Drehmoment gegeben.
Die Größe dieses Drehmoments M ist abhängig von der Größe der Kraft F und vom Hebelarm h. Der Hebelarm ist hierbei der senkrechte Abstand (rechter Winkel) von der Kraft F zum gewählten Bezugspunkt (hier: Schraube).
Wenn wir davon ausgehen, dass die beiden Kräfte F gleich groß sind, so übt die obere Kraft ein größeres Moment auf die Schraube aus, da sie einen größeren senkrechten Abstand h zur Schraube aufweist. Demnach übt die untere Kraft ein kleineres Moment auf die Schraube aus, da ihr Hebelarm h kleiner ist.
Ist kein senkrechter Abstand zu dem gewählten Bezugspunkt gegeben, dann tritt keine Drehbewegung auf, das Drehmoment ist dann Null:
Videoclip: Drehmoment – Erklärung
Im nachfolgenden Video zeige ich dir, was das Drehmoment ist.
Drehmoment – Formel, Beispiel und Berechnung
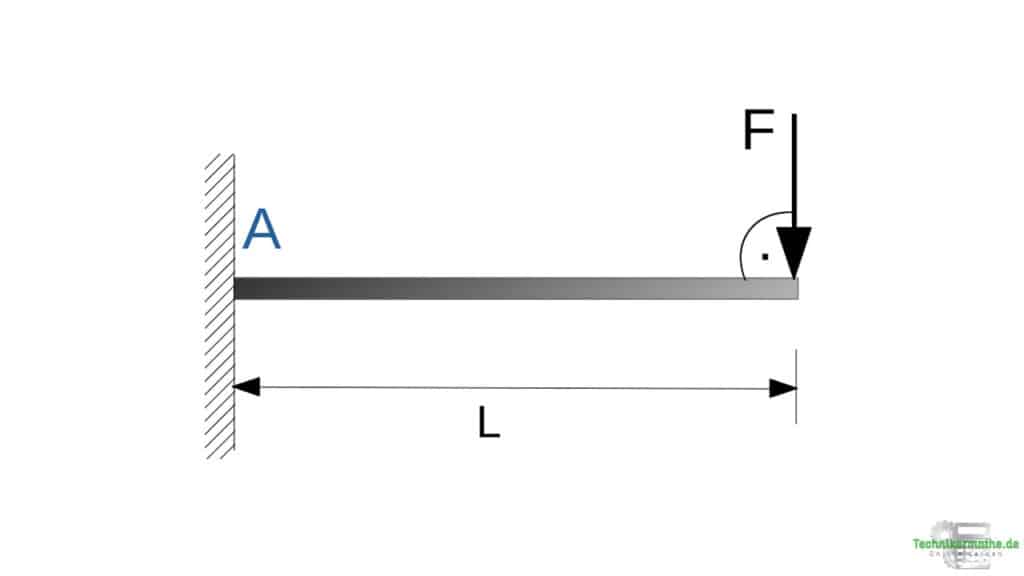
In der obigen Grafik wirkt die Kraft F auf den Balken, welcher fest in der Wand eingespannt ist. Die Frage könnte hier nun lauten:
“Wie groß ist das durch die Kraft F ausgeübte Moment auf den Punkt A bzw. welches Drehmoment muss das Lager A aufnehmen, damit der Balken sich nicht dreht?”
Ein Moment berechnet sich durch die Kraft multipliziert mit dem Hebelarm. Die Berechnung des Drehmoments erfolgt mit der folgenden Formel:
mit
Kraft [N]
senkrechter Abstand von der Kraft zum Drehpunkt [m]
Der Hebelarm h ist der senkrechte Abstand von der Kraft zum gewählten Punkt. Den senkrechten Abstand kannst du leicht ermitteln, indem du dir eine gedankliche Parallelverschiebung der Kraft vorstellst. Und zwar so lange, bis die Wirkungslinie der Kraft den betrachteten Punkt schneidet.
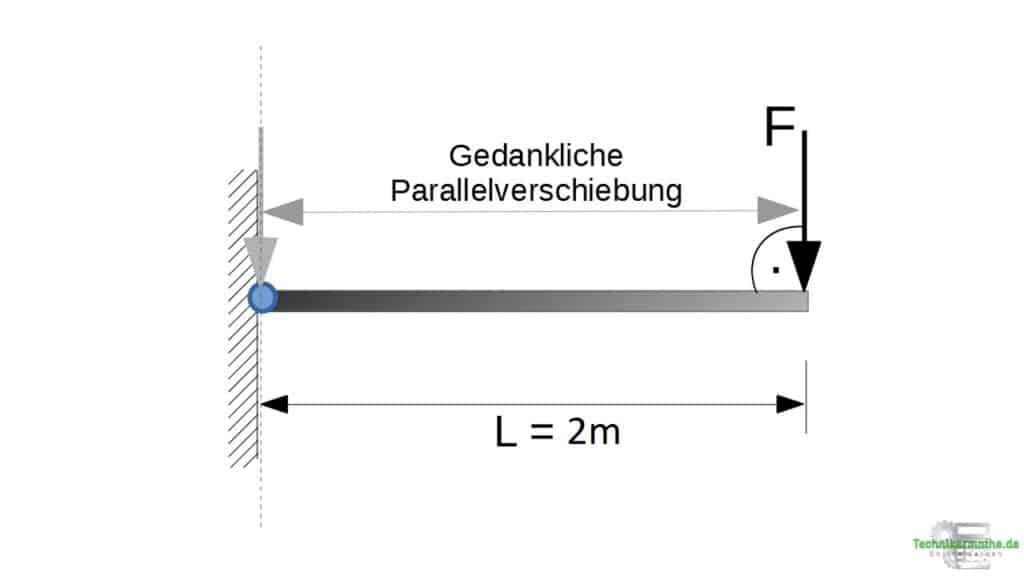
In der obigen Grafik führen wir eine gedankliche Parallelverschiebung der Kraft F solange durch, bis die Wirkungslinie (die Verlängerung der Kraft) den Bezugspunkt (blauer Punkt) schneidet. Der Weg der Parallelverschiebung entspricht dem Hebelarm. Im obige Beispiel ergibt sich also ein Hebelarm von L = 2m.
Das Moment lässt sich jetzt einfach berechnen:
Die Kraft F = 100N übt demnach auf den Punkt A ein Moment von 200 Nm aus. Die Einheit eines Moments ist Newtonmeter (Nm) oder ein Vielfaches davon, z.B. kNm, Ncm.
Was passiert mit dem Drehmoment, wenn sich der Abstand verkleinert bzw. vergrößert?
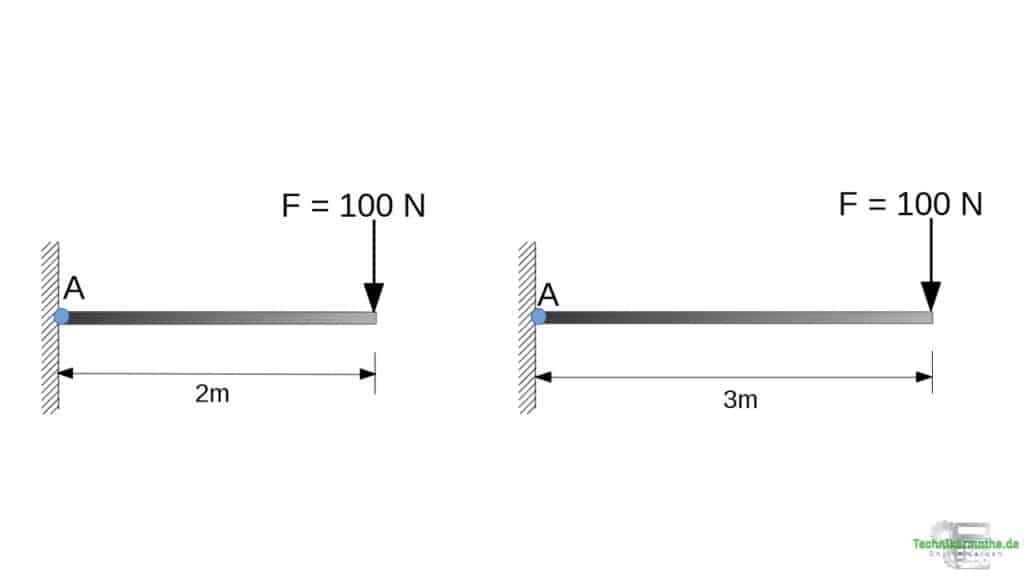
In der oberen Grafik ist der rechte Hebelarm (3m) größer als in der linke Hebelarm (2m). Die Kraft hingehen weist dieselbe Größe auf. Das Moment, welches die Kraft jeweils auf den Punkt 
ausübt, ergibt sich zu:
(links)
(rechts)
Der Hebelarm hat also eine Auswirkung auf die Größe des Moments.
Je größer der Hebelarm, desto größer auch das wirkende Moment.
Was passiert mit dem Drehmoment, wenn sich die Größe der wirkenden Kraft ändert?
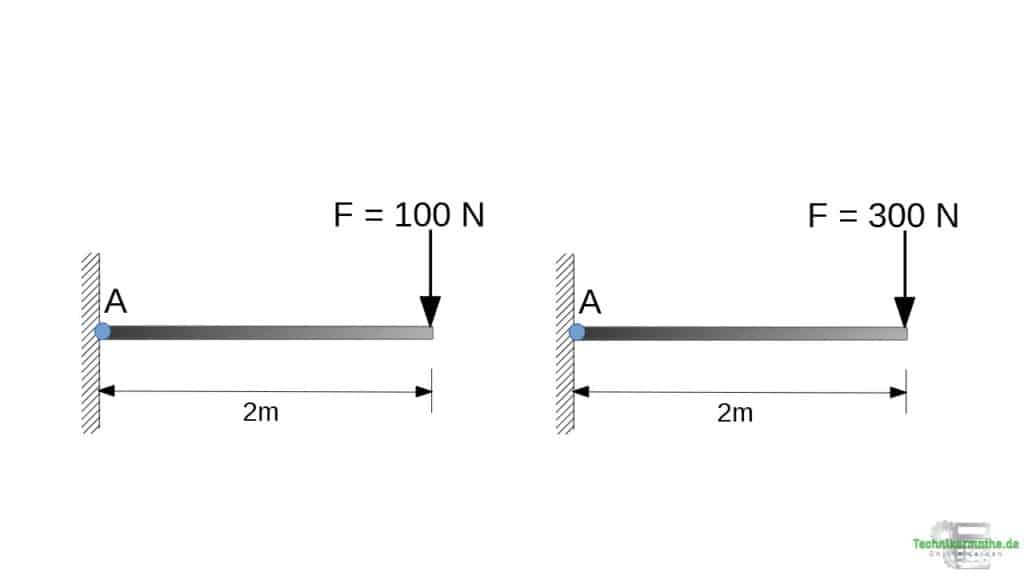
In der oberen Grafik ist die rechte Kraft größer als die linke Kraft. Der Hebelarm ist in beiden Fällen gleich groß, also konstant. Das Moment, welches die Kraft jeweils auf den Punkt ausübt, ergibt sich somit zu:
(links)
(rechts)
Die Größe der Kraft hat also eine Auswirkung auf die Größe des Moments.
Je größer die Kraft, desto größer auch das wirkende Moment.
Linksdrehendes oder rechtsdrehendes Moment
Wir müssen bei den Momenten noch linksdrehende und rechtsdrehende Momente voneinander unterschieden. Das ist für die spätere Berechnung von Auflagerkräften aus den Gleichgewichtsbedingungen notwendig.
Ein linksdrehendes Moment dreht den Körper in einer Linksdrehung (gegen den Uhrzeigersinn) um den gewählten Punkt.
Ein rechtsdrehendes Moment dreht den Körper in einer Rechtsdrehung (mit dem Uhrzeigersinn) um den gewählten Punkt.
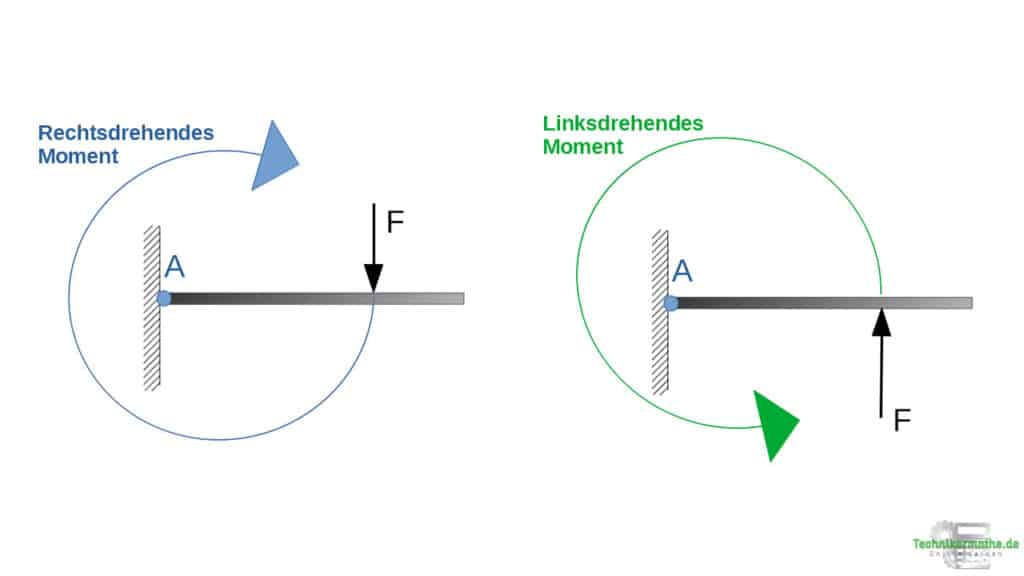
Du siehst in den beiden Grafiken ein rechtsdrehendes Moment (links) und ein linksdrehendes Moment (rechts). Zur Bestimmung, ob es sich um ein links- oder rechtsdrehendes Moment handelt, stellst du dir einfach die folgende Frage:
In welche Richtung dreht die Kraft den Balken um den gewählten Punkt A?
Video: Momente berechnen – Links- oder rechtsdrehendes Moment
Ich zeige dir im folgenden Video, wie du herausfindest, ob es sich um ein links- oder rechtsdrehendes Moment handelt.
Nachdem du jetzt einen ausführlichen Überblick zu dem Thema Drehmoment erhalten hast und nun weißt wie du hier Größen zu berechnen hast, wollen wir uns in der nachfolgenden Lerneinheit dein Wissen noch weiter vertiefen und mit die einige weitere Beispiele zur Berechnung von Drehmomenten anschauen.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben
Quizfrage 1
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team
