PH2 – Kräftezerlegung [Erklärung, Beispiel, Video]

Bei der Kräftezerlegung wird eine einzelne Kraft in mehrere Komponenten zerlegt, die entlang verschiedener Richtungen wirken. Dies wird oft durchgeführt, um die Auswirkungen einer Kraft in einem bestimmten Kontext besser zu verstehen oder um Probleme in der Mechanik zu lösen.

Die einfachste Form der Kräftezerlegung ist die Zerlegung einer Kraft in zwei Komponenten entlang der y-Achse und der x-Achse. Dies wird oft als Zerlegung in x- und y-Richtungen bezeichnet. Die Zerlegung einer schrägen Kraft (Kraft mit Winkel) erfolgt, damit die Komponenten der Kraft innerhalb der Gleichgewichtsbedingungen berücksichtigt werden kann., z.B. zur Berechnung der Auflagerkräfte oder Schnittgrößen.

In dieser Lektion schauen wir uns die Zerlegung einer Kraft in zwei Kraftkomponenten an. Dieses Vorgehen wird auch als Kräftezerlegung bzw. Zerlegung einer Kraft bezeichnet.

Für ein optimales Verständnis helfen dir ein Videoclip und zwei ausführliche Beispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Kräftezerlegung – Grundlegendes

Unter der Kräftezerlegung versteht man, die Zerlegung einer einzelnen Kraft in mindestens zwei Teilkräfte, die in unterschiedliche Richtungen wirken.

Merk’s dir!

Die Kräftezerlegung ist für spätere Berechnungen und für deiner Prüfung sehr wichtig. Deswegen ist es notwendig, dass du diese Methode sicher beherrschst.

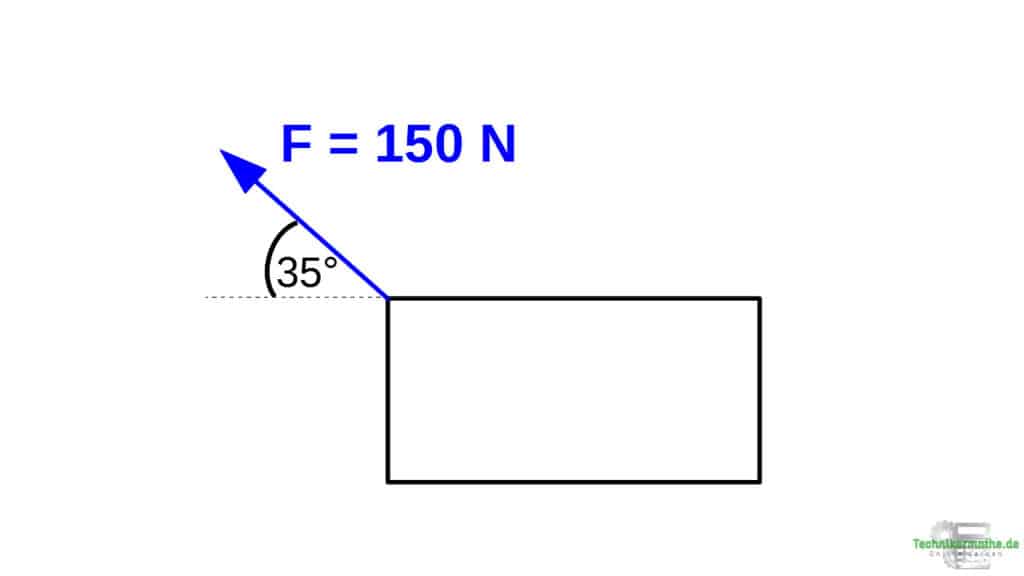
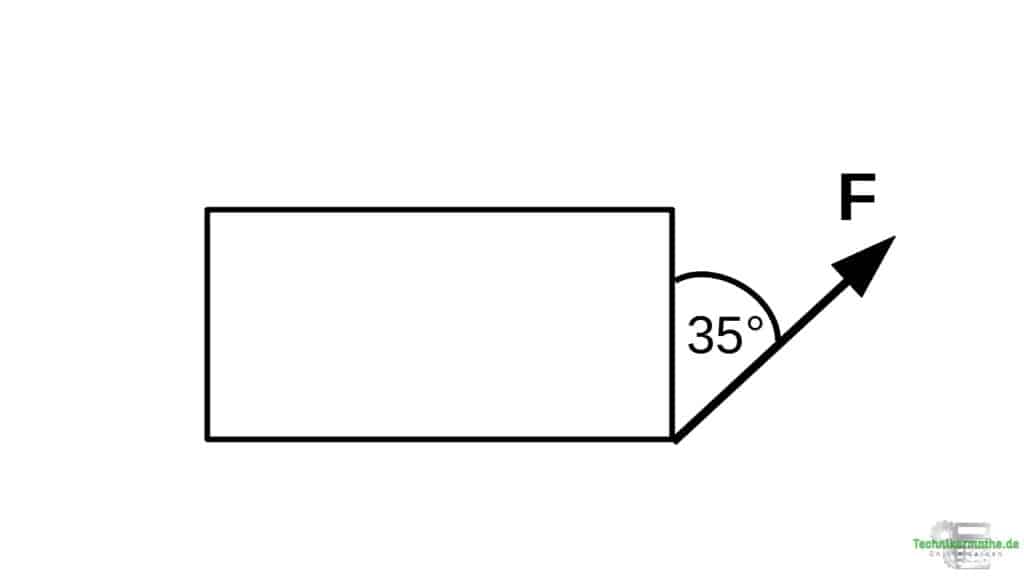
Schauen wir uns nun an, wie du eine Kraft in zwei Kräfte zerlegst. Die beiden Kräfte ersetzen dabei die gegebene Kraft. Stellen dir dazu eine Kiste vor, an welche eine Kraft F angreift:

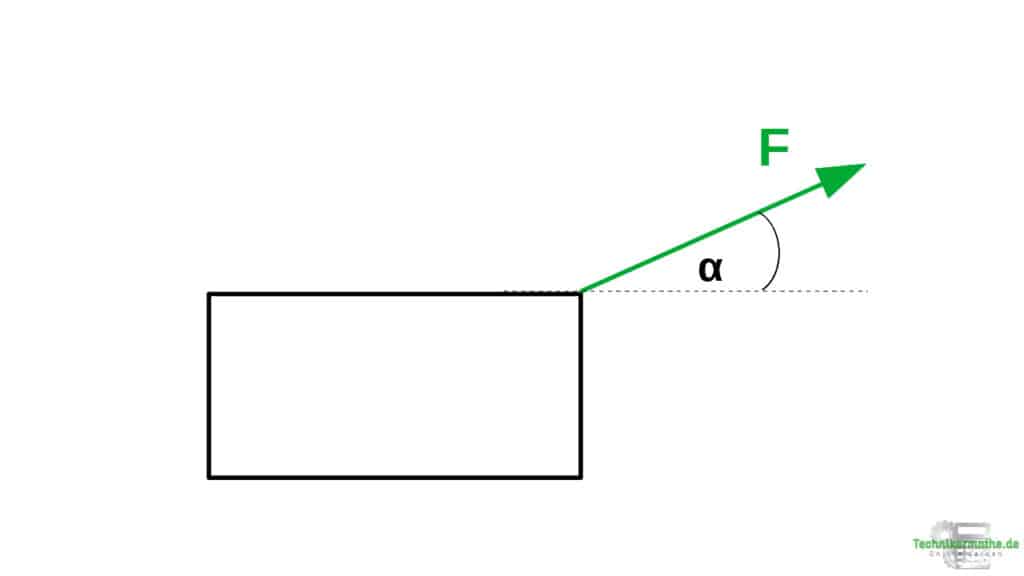
Zerlegung einer Kraft, Kräftezerlegung, zwei Kräfte, Sinus, Kosinus, Cosinus — Vorgehensweise: Kräftezerlegung einer Kraft

Auf die obige Kiste wirkt die Kraft F mit einem Winkel α zur Horizontalen (gestrichelte Linie). Für die analytische Berechnung muss immer der Winkel von der gegebenen Kraft zur Horizontalen oder zur Vertikalen gegeben sein, damit die Kräftezerlegung durchgeführt werden kann.

Vorgehensweise: Kräftezerlegung

Schritt 1: Gegebene Kraft mit Anfangspunkt in ein x,y-Koordinatensystem legen. Gegebenenfalls Winkel zur x-Achse bestimmen.

Schritt 2: Unter Anwendung von Sinus und Kosinus wird die gegebene Kraft in eine Kraftkomponente in x-Richtung und in y-Richtung zerlegt.

Schritt 3: Die beiden berechneten Kräfte ersetzen die alte Kraft.

Schritt 1: Koordinatensystem

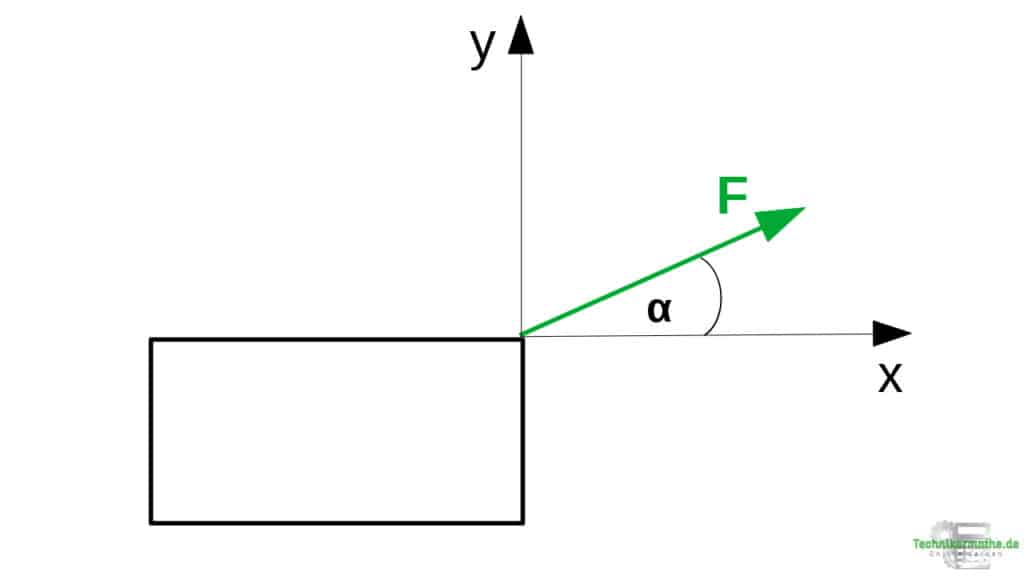
Kräftezerlegung, Zerlegung einer Kraft, Winkel, Sinus, Kosinus, Beispiel, Koordinatensystem — Kräftezerlegung: Einführung eines Koordinatensystems

Die gegebene Kraft wird mit ihrem Anfangspunkt in den Koordinatenursprung gelegt. Dabei wird der Winkel mit eingezeichnet. Ist der Winkel zur Vertikalen gegeben, so kannst du den Winkel zur Horizontalen einfach berechnen, indem du diesen von 90° abziehst. Es sollte also immer der Winkel von der gegebenen Kraft zur Horizontalen (also zur x-Achse) betrachtet werden.

Schritt 2: Kräftezerlegung

Im 2. Schritt geht es um die eigentliche Kräftezerlegung. Wir wollen die gegebene Kraft in die beiden Kräfte F_x (in x-Richtung) und F_y (in y-Richtung) zerlegen:

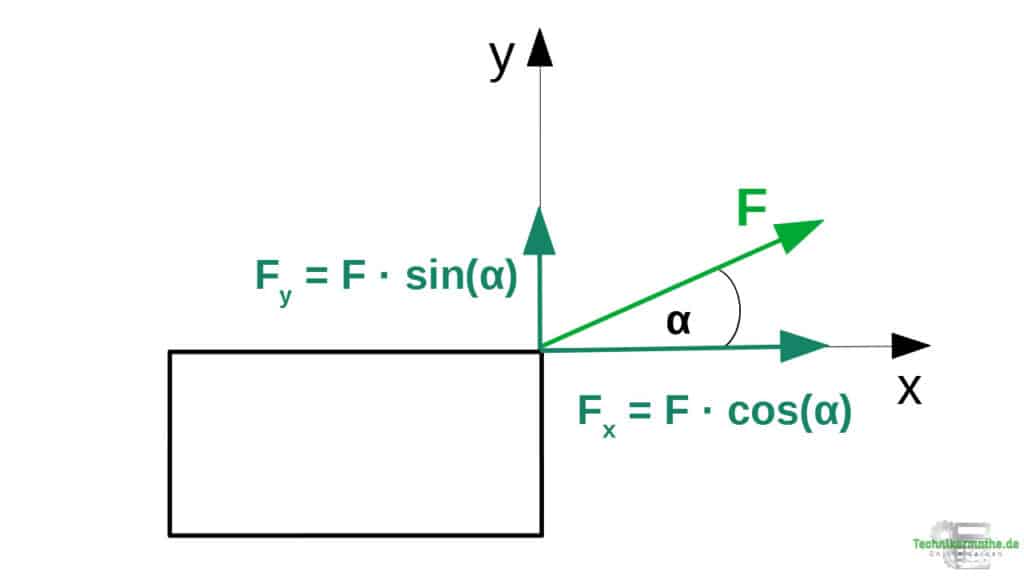
Kräftezerlegung, Zerlegung einer Kraft, Cosinus, Kosinus, Sinus, Beispiel, Komponenten — Kräftezerlegung: Komponenten berechnen

Hierfür benötigen wir den Sinus und den Kosinus des gegebenen Winkels. Dabei gilt:

Ist der eingeschlossene Winkel von der Kraft zur x-Achse gegeben, so ist 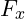$F_x$ die Ankathete und wird mittels Kosinus berechnet. In diesem Fall wird 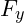$F_y$ mittels Sinus berechnet.
Ist der eingeschlossene Winkel von der Kraft zur y-Achse gegeben, so ist 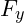$F_y$ die Ankathete und wird mittels Kosinus berechnet. In diesem Fall wird 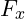$F_x$ mittels Sinus berechnet.

Merk’s dir!

Merk dir Fall 1 und berechne immer den Winkel von der gegebenen Kraft F zur x-Achse. So kannst du die Kräftezerlegung immer wie folgt durchführen:

$F_x = F \cdot \cos(\alpha)$

$F_y = F \cdot \sin(\alpha)$

Schritt 3: Kraft ersetzen

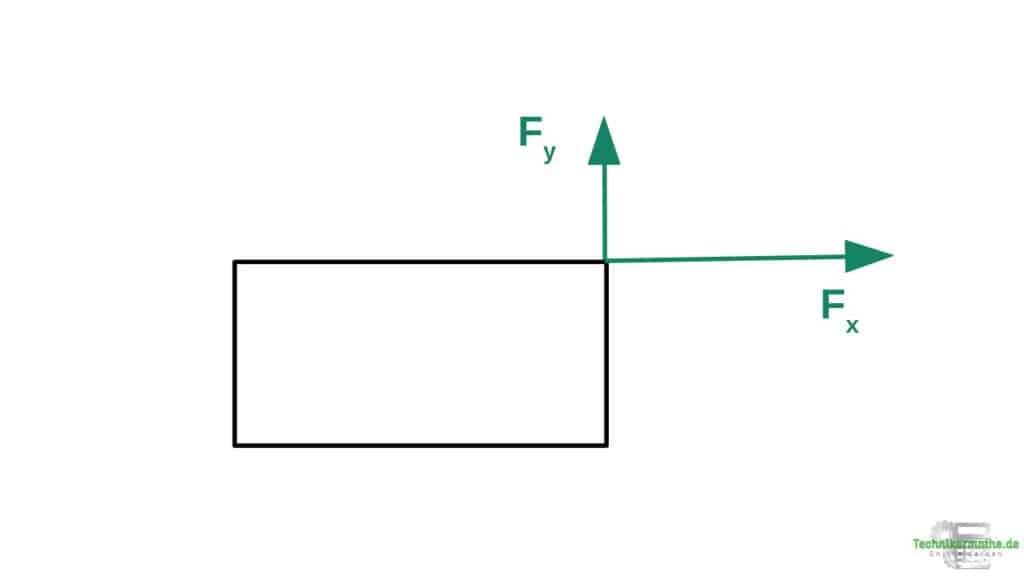
Kräftezerlegung, Kraftkomponenten, Berechnung, Komponenten, Sinus, Kosinus — Kräftezerlegung: Kraft ersetzen

In der obigen Grafik haben wir die Kraft F durch ihre beiden Komponenten ersetzt. Die beiden Kräfte F_x und F_y üben dieselbe Wirkung auf die Kiste aus, wie die beiden Kräfte zusammen.

Merk’s dir!

Bei der späteren Berechnung der Auflagerkräfte musst du wissen, wie eine Kraft in ihre zwei Komponenten zerlegt wird. Ist also in der Aufgabenstellung eine Kraft mit Winkel gegeben, so musst du diese zunächst in ihre beiden Komponenten zerlegen und die Kraft mit Winkel ersetzen. Danach kannst du die Gleichgewichtsbedingungen anwenden.

Videoclip: Kräftezerlegung

Im folgenden Video schauen wir uns die Kräftezerlegung an. Jessica erklärt dir ganz einfach, wie du hier vorgehen musst.

Schauen wir uns dazu mal zwei Beispiele an.

In den folgenden Beispielen lernst du, wie du eine Kraft in ihre beiden Komponenten zerlegst:

Beispiel 1: Zerlegung einer Kraft im 2. Quadranten

Beispiel 2: Zerlegung einer Kraft im

Beispiel 1: Zerlegung einer Kraft im 2. Quadranten

Aufgabenstellung

Kräftezerlegung, Beispiel, Zerlegung einer Kraft — Beispiel zur Kräftezerlegung einer Kraft

Gegeben sei eine Kiste, an welche die Kraft F = 150 N mit einem Winkel von 35° zur Horizontalen angreift.

Führe eine Kräftezerlegung durch!

1.Schritt: Koordinatensystem

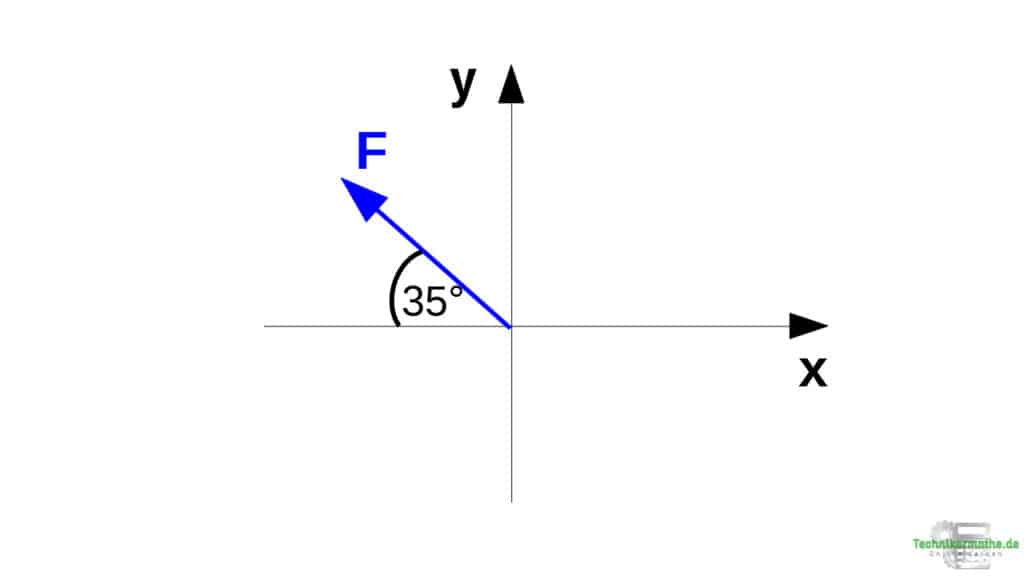
Beispiel, Kräftezerlegung, Winkel, Zerlegung einer Kraft — Beispiel: Zerlegung einer Kraft

Zunächst wird die Kraft mit dem Anfangspunkt in das Koordinatensystem legen. Die Kraft befindet sich im 2. Quadranten (siehe Grafik).

2.Schritt: Kraftkomponenten berechnen

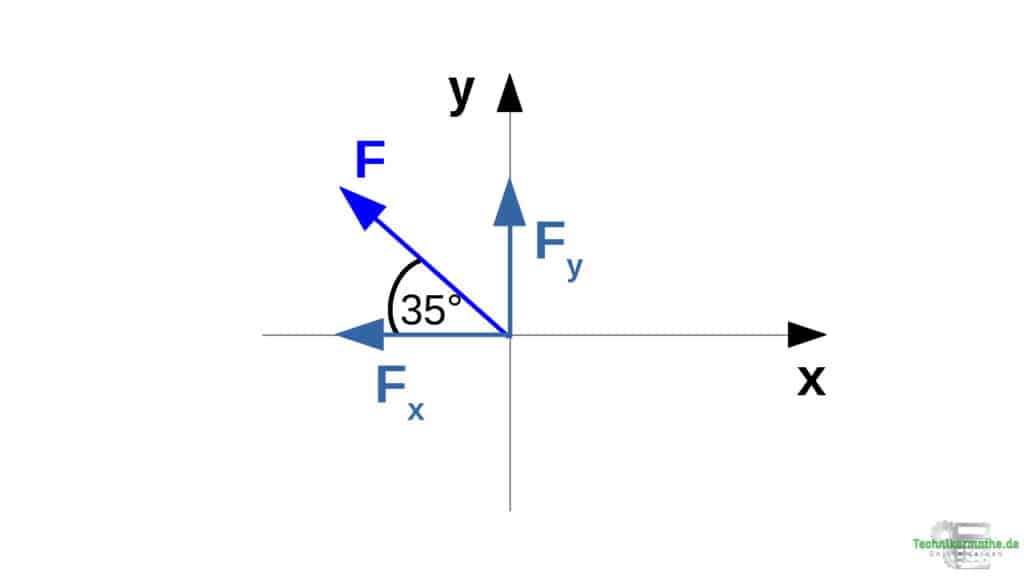
Komponenten berechnen, Zerlegung einer Kraft, Kräftezerlegung, Koordinatensystem, 2. Quadrant, Komponenten — Zerlegung einer Kraft in ihre x- und y-Komponente

Da der Winkel zur x-Achse gegeben ist, ist F_xdie Ankathete und wird mit dem Kosinus berechnet. F_ywird somit mit dem Sinus berechnet:

$F_x = F \cdot \cos(35{\circ}) = 150 N \cdot \cos(35{\circ}) = 122,87 N$

$F_y = F \cdot \sin(35{\circ}) = 150 N \cdot \sin(35{\circ}) = 86,04 N$

Die Kraftkomponente F_x ist größer als F_y. Das liegt daran, weil die gegebene Kraft F näher an der x-Achse liegt als an der y-Achse. Damit ist die Wirkung in x-Richtung größer als in y-Richtung.

3.Schritt: Kraft ersetzen

Kräfterzelgung, Techniker, Nachhilfe, Zerlegung einer Kraft, Komponenten, Beispiel — Zerlegung einer Kraft: Kraft ersetzen

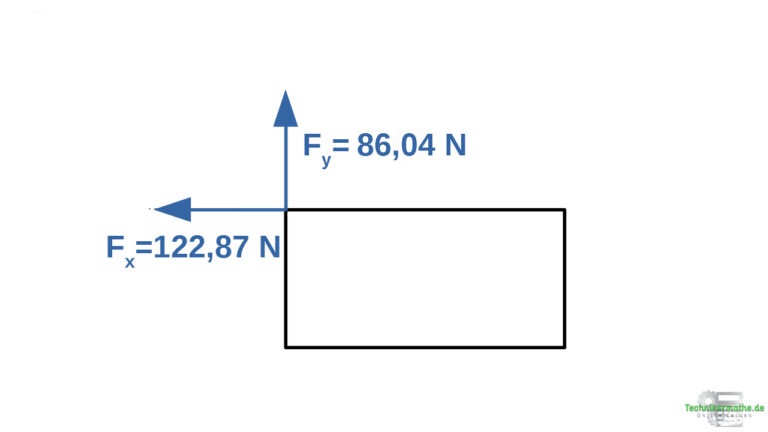
Im dritten und letzten Schritt wird die Kraft F durch die beiden berechneten Kraftkomponenten ersetzt. Diese üben dieselbe Wirkung auf die Kiste aus.

Beispiel 2 : Zerlegung einer Kraft im 1. Quadranten

Aufgabenstellung

Zerlegung einer Kraft, Kräftezerlegung, Beispiel, Berechnung, Vorgehensweise, 1. Quadrant — Beispiel: Kräftezerlegung

Gegeben sei die obige Kiste, an welche die Kraft F = 100 N angreift.

Führe eine Kräftezerlegung durch!

1.Schritt: Koordinatensystem

Zunächst legen wir die Kraft F mit dem Anfangspunkt in den Koordinatenursprung. Die Kraft F liegt im 1. Quadranten.

Gegeben ist der Winkel von der Kraft F zur Vertikalen mit 35°. Wir berechnen den Winkel zur Horizontalen:

$90^{\circ} - 35{\circ} = 55{\circ}$

2.Schritt: Komponenten berechnen

Jetzt können wir die x-Komponente mit dem Kosinus berechnen und die y-Komponente mit dem Sinus.

$F_x = F \cdot \cos(55{\circ}) = 100 N \cdot \cos(55{\circ}) = 57,36 N$

$F_y = F \cdot \sin(55{\circ}) = 100 N \cdot \sin(55{\circ}) = 581,92 N$

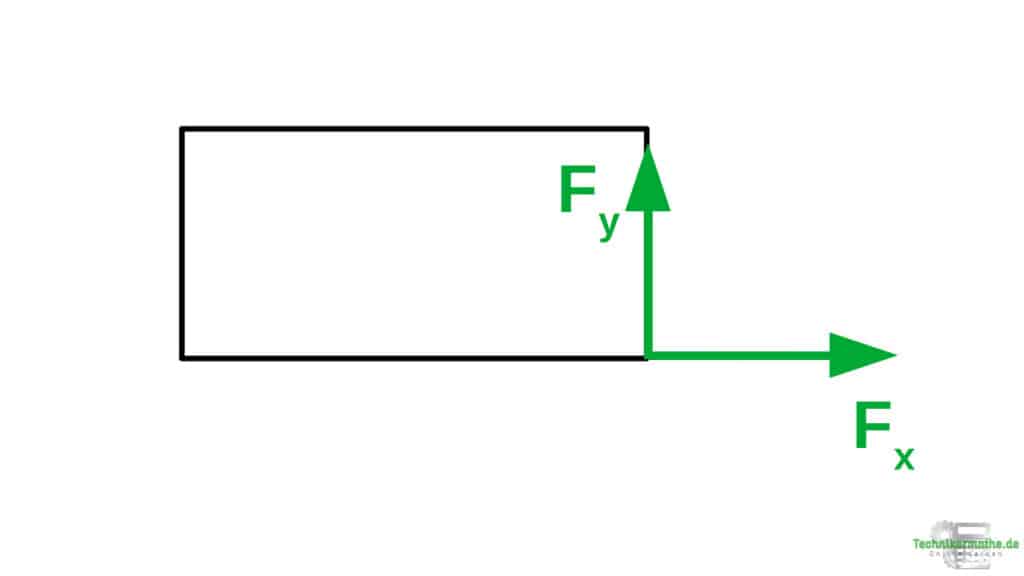
3.Schritt: Kraft F ersetzen

Wir ersetzen nun die Kraft F durch ihre beiden Komponenten:

Kräftezerlegung, Lösung, Komponenten, Zerlegung einer Kraft, — Kräftezerlegung: Komponenten einfügen

Was kommt als Nächstes?

Nachdem wir uns jetzt ausführlich mit dem Thema Kräftezerlegung beschäftigt haben und du nun weißt, wie Größen in diesem Zusammenhang berechnet werden, geben wir dir in der folgenden Lerneinheit eine ausführliche Übersicht über die Gleichungen, die du für die Berechnung der Resultierenden aus zwei Kräften benötigst.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++