PH2 – Betrag der Resultierenden (Kosinussatz) [Formel, Beispiel, Video]

Den Betrag der Resultierenden aus zwei gegeben Kräften kann mittels Kosinussatz berechnet werden, wenn die beiden gegebenen Kräfte einen Winkel zueinander aufweisen. Die Resultierende ist die Zusammenfassung der beiden Kräfte zu einer einzigen Kraft und übt die gleiche Wirkung auf den Körper aus, wie die beiden Kräfte zusammen.

In dieser Lerneinheit schauen wir uns an, wie du den Betrag der Resultierenden mittels Kosinussatz berechnest.

Für ein optimales Verständnis helfen dir ein Videoclip und ein ausführliches Beispiel zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Kosinussatz: Betrag der Resultierenden

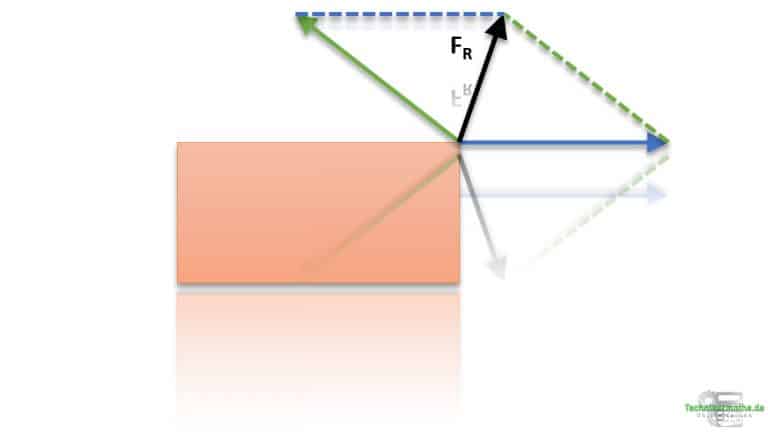
Resultierende bestimmen, Kosinussatz, Resultierende, resultierende Kraft — Resultierende Kraft mittels Kosinussatz

Wir betrachten zwei Kräfte, die einen Winkel zueinander aufweisen, und wollen diese beiden Kräfte zu einer einzigen Kraft zusammenfassen.

Was genau bedeutet das?

Wir wollen nun also diejenige Kraft bestimmen, welche die beiden gegebenen Kräfte F₁ und F₂ ersetzt. Wir benötigen dafür die Größe der resultierenden Kraft F_R und den Winkel von der Resultierenden F_Rzu einer der gegebenen Kräfte, um die Richtung der resultierenden Kraft zu ermitteln.

Ziel ist es, die beiden gegebenen Kräfte durch die Resultierende F_R zu ersetzen. Dabei muss die resultierende Kraft genau dieselbe Wirkung auf den betrachteten Körper ausüben, wie die beiden gegebenen Kräfte zusammen.

Betrag der Resultierenden, Kosinussatz, Resultierende, Zwei Kräfte, Winkel, Parallelogramm, Kräfteparallelogramm — Betrag der Resultierenden mittels Kosinussatz

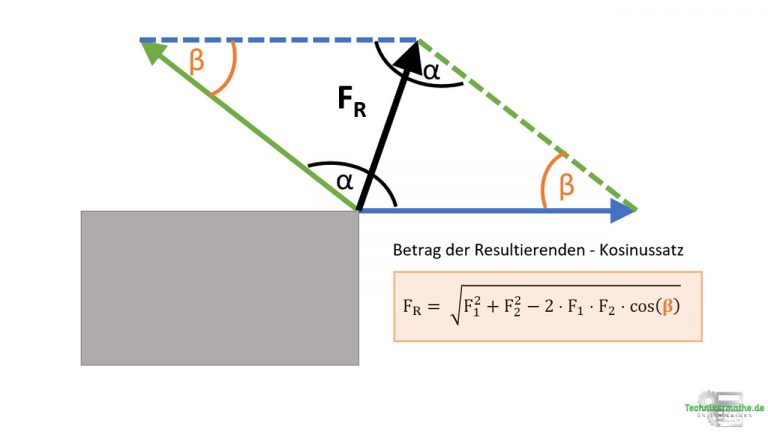
Wir betrachten in dieser Lerneinheit, wie die Größe – also der Betrag – der resultierenden Kraft F_R berechnet wird. Den Betrag der Resultierenden kannst du mittels Kosinussatz wie folgt berechnen:

(1) $F_R = \sqrt{F_1^2 + F_2^2 - 2 \cdot F_1 \cdot F_2 \cdot \cos(\beta)}$

In der Aufgabenstellung ist häufig nicht der Winkel $\beta$ , sondern der Winkel $\alpha$ gegeben. Wir können den Winkel $\beta$ aber ganz einfach aus der Winkelsumme des Kräfteparallelogramms (=360°) berechnen:

$\beta = \frac{360^\circ - 2 \cdot \alpha}{2}$

Häufig wird auch die folgende Gleichung zur Berechnung des Kosinussatzes angegeben:

(2) $F_R = \sqrt{F_1^2 + F_2^2 + 2 \cdot F_1 \cdot F_2 \cdot \cos(\alpha)}$

Bei der Gleichung (1) ergibt sich ein Minuszeichen vor der 2 und hier wird der Winkel β zur Berechnung der Resultierenden berücksichtigt. Bei der Gleichung (2) ergibt sich ein Pluszeichen vor der 2 und hier wird der Winkel α bei der Berechnung verwendet.

Welcher Winkel

Du kannst natürlich beide Formeln zur Berechnung anwenden, du musst eben nur darauf achten, dass die Winkel sich unterscheiden.

Liegen die beiden Kräfte mit ihren Anfangspunkten aneinander, so ist der Winkel dazwischen der Winkel α.
Liegt hingegen die Spitze der einen Kraft am Anfangspunkt der anderen Kraft, so ist der Winkel dazwischen der Winkel β.

Videoclip: Betrag der Resultierenden mittels Kosinussatz

Im nachfolgenden Video schauen wir uns an, wie du den Betrag der Resultierende aus zwei Kräften mittels Kosinussatz berechnen kannst.

Die nachfolgenden Beispiele sollen dir zeigen, wie du die obigen Gleichungen anwendest.

Beispiel: Betrag der Resultierenden aus zwei Kräften

Aufgabenstellung

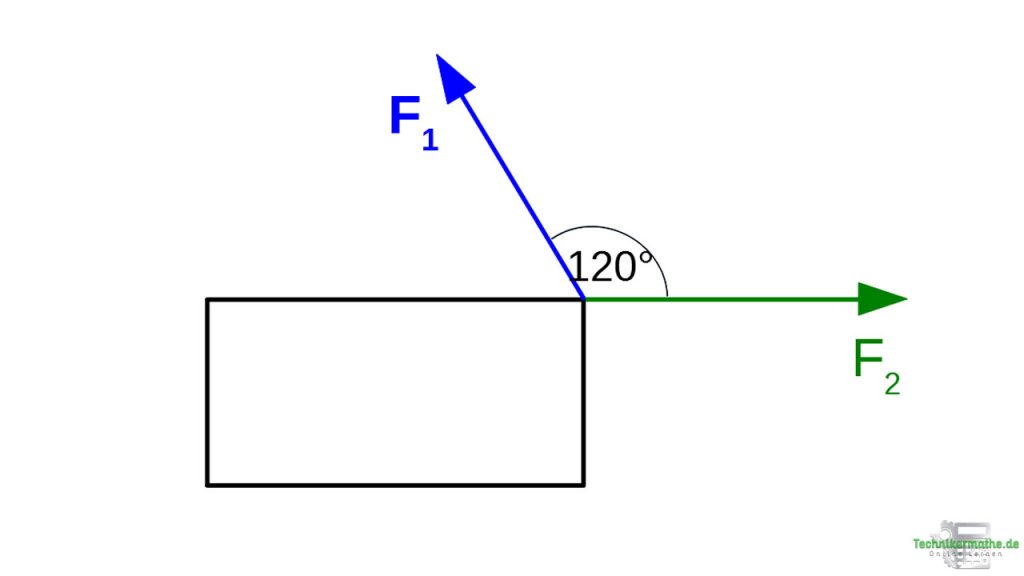
Betrag der Resultierenden, Resultierende bestimmen, Nachhilfe Physik, Techniker, Kosinussatz, Parallelogramm, Kräfteparallelogramm — Beispiel: Betrag der Resultierenden mittels Kosinussatz

Gegeben seien die beiden Kräfte F₁=120N und F₂=90N und der eingeschlossene Winkel von 120°. Wir wollen die beiden Kräfte durch eine einzige Kraft ersetzen.

Wie groß muss diese Kraft sein, damit sie dieselbe Kraft wie die beiden gegebenen Kräfte auf die Kiste ausübt?

Zunächst zeichnen wir skizzenhaft das Kräfteparallelogramm, um uns die Situation besser vorstellen zu können.

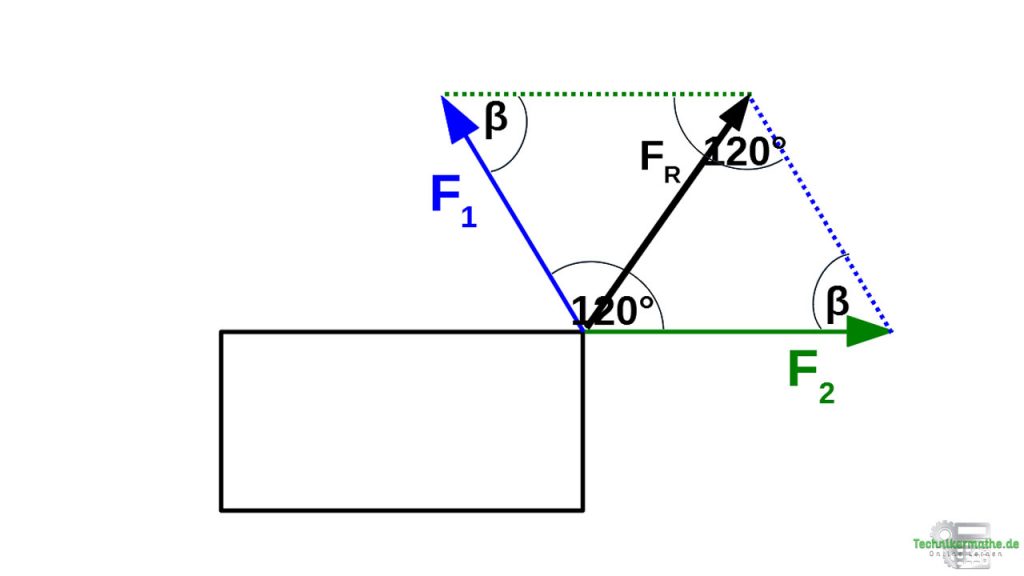
Betrag der Resultierenden, Resultierende bestimmen, Kosinussatz, Kräfteparallelogramm, Zwei Kräfte, Resultierende, resultierende Kraft — Betrag der Resultierenden mittels Kosinussatz: Kräfteparallelogramm

Betrag der Resultierenden mittels Kosinussatz

Zur Berechnung der resultierenden Kraft $F_R$ wenden wir jetzt den Kosinussatz an:

$F_R = \sqrt{F_1^2 + F_2^2 - 2 \cdot F_1 \cdot F_2 \cdot \cos(\beta)}$

Bei dieser Gleichung wird der Winkel β benötigt, welcher sich rechnerisch wie folgt ermitteln lässt:

$360^\circ \degree - 2 \cdot 120^\circ = 2 \cdot \beta$

Hierbei ist die 360° die Summe aller Winkel eines Parallelogramms. Der 120°-Winkel ist der gegebene eingeschlossene Winkel. In einem Parallelogramm sind die gegenüberliegenden Winkel identisch, weshalb der 120°-Winkel zweimal vorkommt. Der verbleibende Winkel ist der gesuchte Winkel β, der ebenfalls zweimal vorkommt.

Es ergibt sich demnach:

$2 \cdot \beta = 120 \circ$

Und damit:

$\beta = 60\circ$

Mit den gegebenen Werten können wir die resultierende Kraft F_R berechnen:

$F_R = \sqrt{(120N)^2 + (90 N)^2 - 2 \cdot 120 N \cdot 90 N \cdot \cos(60°)}$

$F_R = 108,17 N$

Um die beiden Kräfte F₁ und F₂ zu ersetzen, müssen wir die Kraft F_R mit einem Betrag von 108,17 N an die Kiste anbringen.

Alternativ verwendest du die folgende Gleichung und kannst direkt den Winkel einsetzen, denn α = 120°:

(2) $F_R = \sqrt{F_1^2 + F_2^2 + 2 \cdot F_1 \cdot F_2 \cdot \cos(\alpha)}$

Einsetzen der Werte:

$F_R = \sqrt{120^2 + 90^2 + 2 \cdot 120 \cdot 90 \cdot \cos(120^\circ)} = 108,17 N$

Wir kennen nun also die Größe bzw. den Betrag der anzubringenden Kraft, aber noch nicht in welche Richtung die Kraft wirken muss, damit auch wirklich genau dieselbe Wirkung auf die Kiste ausgeübt wird, wie von den beiden gegebenen Kräften F₁ und F₂. Die Richtung der Resultierenden betrachten wir in der folgenden Lerneinheit mittels Sinussatz.

Was kommt als Nächstes?

In der nachfolgenden Lerneinheit betrachten wir, wie die Richtung der Resultierenden bestimmt wird.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++