PH2 – Gewichtskraft: Berechnung und Angriffspunkt

Die Gewichtskraft ist nichts anderes als die Masse eines Körpers in Kilogramm multipliziert mit der Erdbeschleunigung von 9,81 Meter pro Quadratsekunde. Die Einheit der Gewichtskraft ist damit Newton.

Wir wollen uns in diesem Abschnitt mal eine Kraft anschauen, die dir immer wieder begegnen wird, die Gewichtskraft.

Für ein optimales Verständnis helfen dir drei unterschiedliche Beispiele zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs PH2-Einführung in die Statik.

Schauen wir uns zunächst einmal an, wie die Gewichtskraft definiert wird.

Gewichtskraft – Grundlagen

Gewichtskraft, vertikal nach unten — Gewichtskraft wirkt immer vertikal nach unten

Die Gewichtskraft ist eine Kraft, die infolge der Masse m eines Körpers und der Erdanziehungskraft g resultiert. Jeder Körper mit einer Masse weist demnach eine Gewichtskraft auf, da er auf der Erde der Erdbeschleunigung ausgesetzt ist. Die Gewichtskraft wirkt immer vertikal nach unten und greift im Schwerpunkt des betrachteten Körpers an.

Zum Bild: Stell dir vor du stehst mit deinem Skateboard auf einer Rampe. Dein Gewicht bzw. deine Masse sowie die Masse des Skateboards werden infolge der Erdanziehung auf die Rampe gedrückt. Das Skateboard und du üben also eine Kraft auf die Rampe aus. Diese Kraft ist immer vertikal nach unten gerichtet (Kraftpfeil vertikal nach unten) und wird wie folgt berechnet:

Gewichtskraft

$F_G = m \cdot g$

mit

$m$ Masse des Körpers [kg]

$g = 9,81 \frac{m}{s^2}$ Erdbeschleunigung (genormt)

Merk’s dir!

Ist in der Aufgabenstellung eine Masse $m$ gegeben, so musst du zur Berechnung der Gewichtskraft die obige Gleichung anwenden. Denk daran diese immer vertikal nach unten und in den Schwerpunkt der gegebenen Fläche einzuzeichnen.

Fallbeschleunigung g

Die Fallbeschleunigung g ist abhängig vom betrachteten Planeten, auf dem du dich befindest. Die Fallbeschleunigung auf der Erde wird auch als Erdbeschleunigung bezeichnet und ist an jedem Ort auf der Erde unterschiedliche groß. Berechnungen innerhalb der Physik werden aber mit einem Normwert von g = 9,81 m/s² durchgeführt.

Merk’s dir!

Auf dem Mond beträgt die Fallbeschleunigung:

$g_{Mond} = 1,62 \frac{m}{s^2}$

Auf dem Mars beträgt die Fallbeschleunigung:

$g_{Mars} = 3,69 \frac{m}{s^2}$

Die Fallbeschleunigungen auf Mond und Mars sind geringer als auf der Erde. Damit fallen auch die Gewichtskräfte von Körpern auf diesen Planeten geringer als auf der Erde aus.

Beispiel: 50 kg Kiste!

Die Gewichtskraft einer 50 kg Kiste beträgt auf

…der Erde: $g = 50 kg \cdot 9,81 \frac{m}{s^2} = 490,5 N$

…dem Mond : $g = 50 kg \cdot 1,62 \frac{m}{s^2} = 81 N$

…dem Mars : $g = 50 kg \cdot 3,69 \frac{m}{s^2} = 184,5 N$

Die Gewichtskräfte sind also abhängig vom Ort, an dem du dich befindest.

In den nachfolgenden Beispielen schauen wir uns an, wie die Gewichtskraft berechnet wird und wo genau der Angriffspunkt dieser liegt.

1.Beispiel: Berechnung der Kräfte
2.Beispiel: Kräfte mit derselben Wirkungslinie
3.Beispiel: Kräfte mit unterschiedlichen Wirkungslinien

Beispiel 1: Berechnung der Gewichtskraft

Aufgabenstellung

Gewichtskraft, Gewichtskraft berechnen, Kraft berechnen, Beispiel Gewichtskraft — Beispiel: Gewichtskraft berechnen

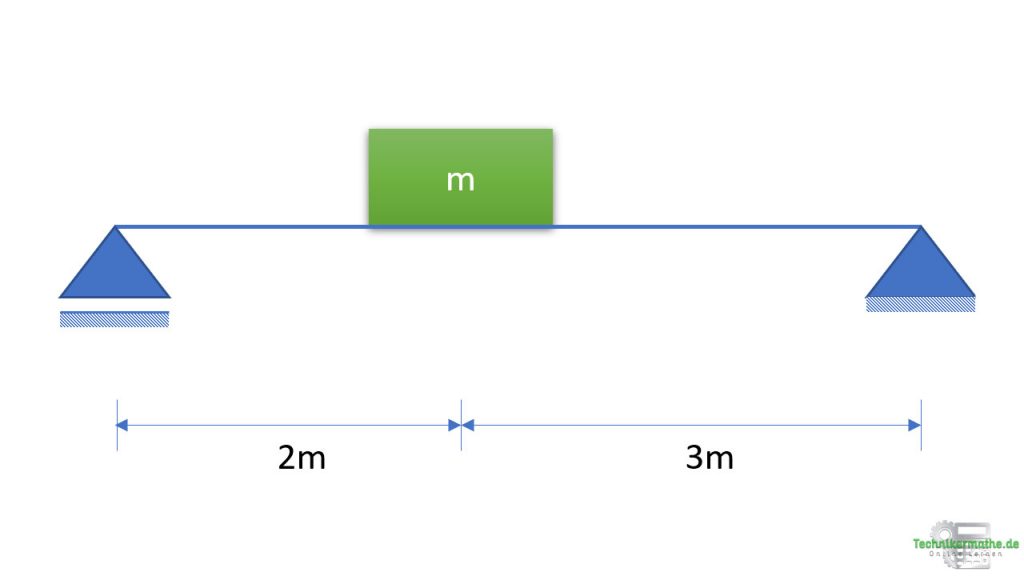
Gegeben sei ein Balken, auf welchem eine Kiste mit dem Gewicht von 50 kg liegt.

a) Welche Kraft übt die Kiste auf den Balken aus?

b) Wo muss diese angreifen (Angriffspunkt)?

a) Kraft berechnen

Zunächst berechnen wir die Gewichtskraft der Kiste:

$F_G = m \cdot g$

Einsetzen von $g = 9,81 \frac{m}{s^2}$ und $m = 50 kg$ :

$F_G = 50 kg \cdot 9,81 \frac{m}{s^2} = 490,5 N$

Die Gewichtskraft der Kiste beträgt 490,5 N und zeigt vertikal nach unten.

b) Angriffspunkt der Gewichtskraft

Wo greift diese Kraft an bzw. wo genau müssen wir diese einzeichnen?

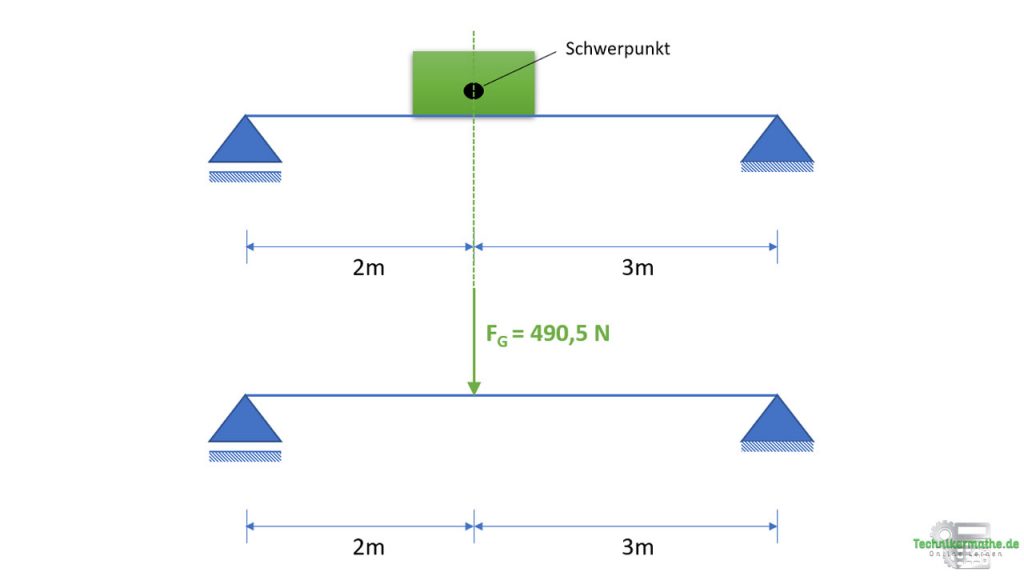
Gewichtskraft, Schwerpunkt, Kraft berechnen, Wirkungslinie, Angriffspunkt, Gewichtskraft berechnen, Masse, Erdbeschleunigung, Fallbeschleunigung — Kiste mit Schwerpunkt und Gewichtskraft

Die Gewichtskraft greift immer im Schwerpunkt der Fläche an. Die Kiste besitzt eine rechteckige Form. Der Schwerpunkt eines Rechtecks/Quadrats/Kreises befindet sich in der Mitte. Demnach greift die Kraft mittig an.

Beispiel 2: Kräfte mit gleicher Wirkungslinie

Aufgabenstellung

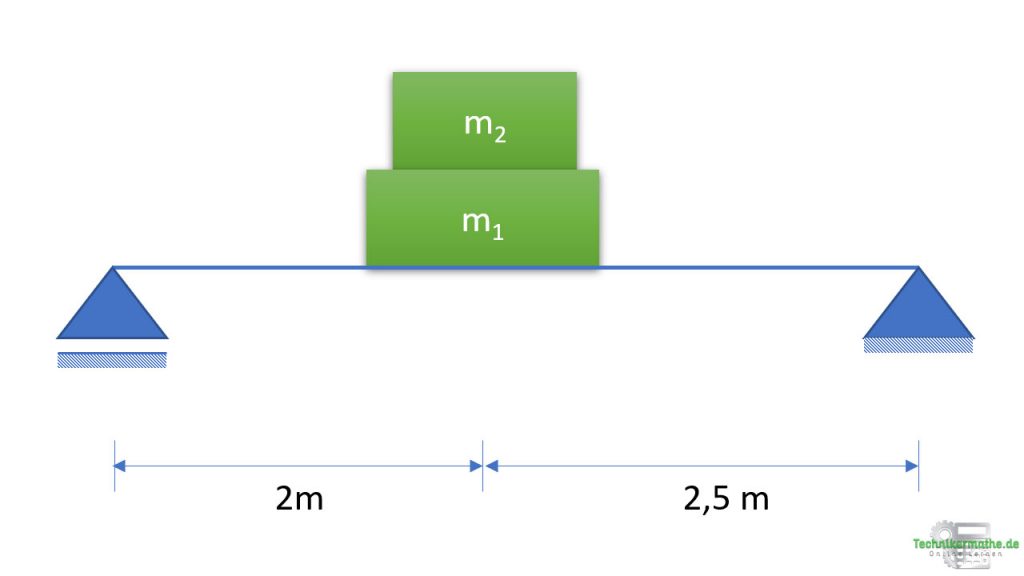
Gewichtskräfte addieren, Gewichtskraft berechnen, Kiste, Kraft berechnen, Gewichtskraft, Kiste, Masse, Beispiel — Beispiel: Gewichtskraft berechnen

Gegeben sei ein Balken, auf welchem eine große Kiste mit dem Gewicht von $m_1 = 100 kg$ liegt. Darauf liegt eine weitere Kiste mit der Masse von $m_2 = 20 kg$ .

a) Welche Gewichtskräfte üben beide Kisten auf den Balken aus?

b) Wo müssen die Gewichtskräfte angreifen (Angriffspunkt)?

a) Gewichtskräfte berechnen

Zunächst berechnen wir die Gewichtskraft der großen Kiste:

$F_G = m \cdot g$

Einsetzen von $g = 9,81 \frac{m}{s^2}$ und $m = 100 kg$ :

$F_{G1} = 100 kg \cdot 9,81 \frac{m}{s^2} = 981 N$

Die Kraft der großen Kiste beträgt 981 N und zeigt vertikal nach unten.

Die Kraft der kleinen Kiste beträgt:

$F_{G2} = 20 kg \cdot 9,81 \frac{m}{s^2} = 196,2 N$

Die Gewichtskraft der kleinen Kiste beträgt 196,2 N und zeigt vertikal nach unten.

b) Angriffspunkt bestimmen

Wo greifen die Gewichtskräfte an bzw. wo genau müssen wir diese einzeichnen?

Gewichtskräfte addieren, Gewichtskraft berechnen, Wirkungslinie, Schwerpunkt, Kiste — Schwerpunkte und Gewichtskräfte einzeichnen

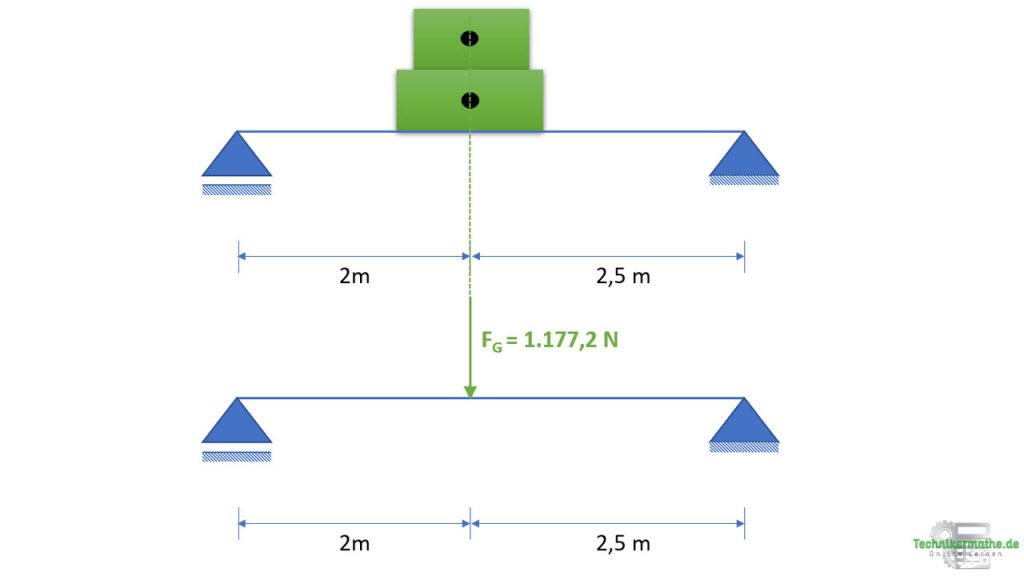
Gewichtskräfte greifen immer im Schwerpunkt der Fläche an. Die Kisten besitzen jeweils eine rechteckige Form. Der Schwerpunkt eines Rechtecks/Quadrats/Kreises befindet sich in der Mitte. Demnach greifen die Gewichtskräfte jeweils mittig an. Da beide auf derselben Wirkungslinie liegen (die beiden Wirkungslinien fallen zusammen), können wir die beiden Gewichtskräfte miteinander addieren:

$F_{G,ges} = 981 N + 196,2 N = 1.177,2 N$

Die beiden Gewichtskräfte werden zu einer Kraft zusammengefasst. Grund dafür ist, dass die Schwerpunkte der beiden Kisten übereinander liegen und damit auch die Wirkungslinien der beiden Kräfte auf einer Linie liegen. Da beiden vertikal nach unten wirken, werden beide Kräfte miteinander addiert.

Merk’s dir!

Gewichtskräfte dürfen nur dann addiert werden, wenn sie auf einer Wirkungslinie liegen.

Beispiel 3: Kräfte mit unterschiedlichen Wirkungslinien

Aufgabenstellung

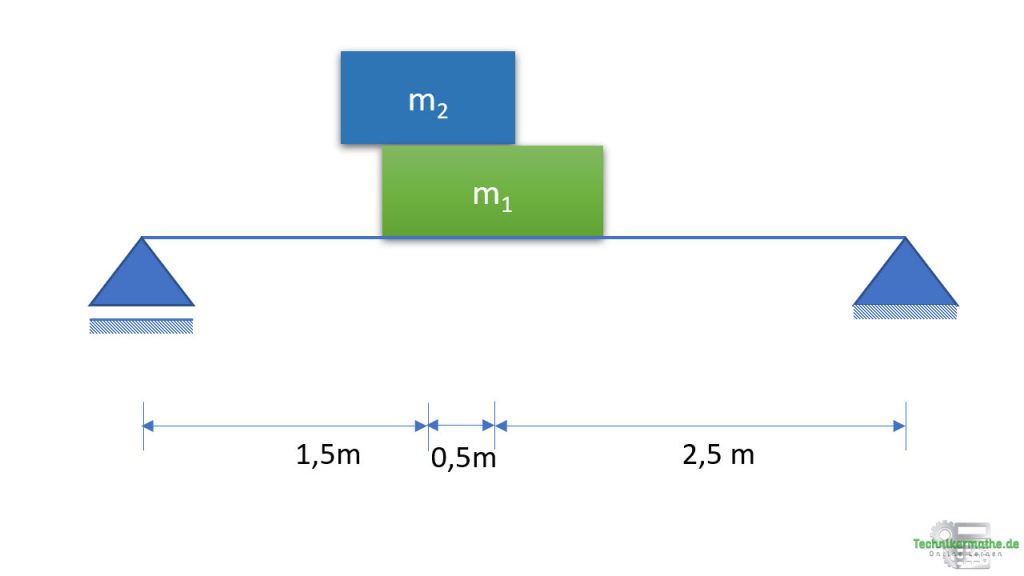
Gewichtskräfte addieren, Gewichtskraft berechnen, Gewichtskraft, unterschiedliche Wirkungslinien, Beispiel, Wirkungslinie — Beispiel: Gewichtskräfte und Angriffspunkte bestimmen

Gegeben sei ein Balken, auf welchem eine große Kiste mit dem Gewicht von $m_1 = 80 kg$ liegt. Darauf liegt eine weitere Kiste mit der Masse von $m_2 = 8 kg$ .

a) Welche Gewichtskräfte üben beide Kisten auf den Balken aus?

b) Wo müssen die Gewichtskräfte angreifen (Angriffspunkt)?

a) Gewichtskräfte berechnen

Zunächst berechnen wir die Gewichtskraft der großen Kiste:

$F_G = m \cdot g$

Einsetzen von $g = 9,81 \frac{m}{s^2}$ und $m_1 = 80 kg$ :

$F_{G1} = 80 kg \cdot 9,81 \frac{m}{s^2} = 784,8 N$

Die Kraft der großen Kiste beträgt 784,8 N und zeigt vertikal nach unten.

Die Kraft der kleinen Kiste beträgt:

$F_{G2} = 8 kg \cdot 9,81 \frac{m}{s^2} = 78,48 N$

Die Gewichtskraft der kleinen Kiste beträgt 78,48 N und zeigt vertikal nach unten.

b) Angriffspunkte berechnen

Wo greifen diese Kräfte an bzw. wo genau müssen wir diese einzeichnen?

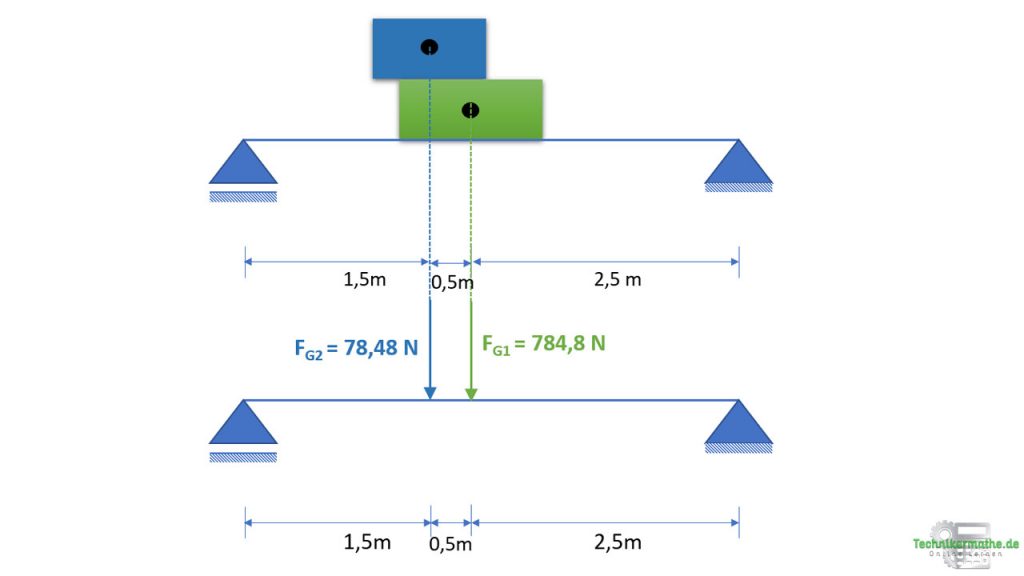
Diese Kräfte greifen immer im Schwerpunkt der Fläche an. Die Kisten besitzen jeweils eine rechteckige Form. Der Schwerpunkt eines Rechtecks/Quadrats/Kreises befindet sich in der Mitte.

Demnach greifen sie jeweils mittig an. In diesem Fall fallen die Wirkungslinien der beiden Kisten jedoch nicht zusammen, weil die Schwerpunkte der beiden Kisten nicht genau übereinander liegen.

Wir dürfen sie nicht miteinander addieren, sondern müssen beide Kräfte einzeichnen.

Merk’s dir!

Bei der späteren Berechnung der Auflagerkräfte wird, innerhalb der Momentengleichgewichtsbedingung, die Summe alle Momente berechnet. Hierfür werden die Abstände zu einem festgelegten Punkt benötigt. Deswegen ist es wichtig, die Kräfte an der richtigen Stelle anzubringen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++