PH1 – Dichte und Dichteanomalie

In dieser Lerneinheit schauen wir uns die Dichte von Körpern an.

Für ein optimales Verständnis helfen dir zwei Videoclips und vier Beispiele zu dem Thema.

Mehr zu diesem Thema und der Physik findest du im Kurs: PH1 – Grundlagen der Physik.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Videoclip: Dichte bestimmen

Im nachfolgenden Video zeigt dir Jessica anhand von zwei Beispielen, wie du die Dichte berechnen kannst:

Lernclip: Dichte bestimmen

Dichte – Grundlagen

Die Dichte ρ (griechischer Buchstabe “rho”) eines Körpers ist nichts anderes als der Quotient aus der Masse (in Kilogramm) und dem Volumen (in Kubikmeter) des Körpers.

Was sind Dichte und Dichteanomalie?

Die Konzepte der Dichte und der Dichteanomalie sind in der Physik und Chemie von großer Bedeutung. Die Dichte beschreibt die Masse pro Volumeneinheit eines Stoffes, während die Dichteanomalie sich auf ungewöhnliche Veränderungen der Dichte unter bestimmten Bedingungen bezieht.

Dichte

Grundprinzipien

Definition: Die Dichte 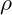$\rho$ eines Materials ist definiert als seine Masse (m) pro Volumeneinheit (V). Die Formel lautet:
$\rho = \frac{m}{V}$
Hierbei wird die Dichte in Kilogramm pro Kubikmeter (kg/m³) gemessen.
Einheiten:
- Kilogramm pro Kubikmeter (kg/m³)
- Gramm pro Kubikzentimeter (g/cm³)
- Kilogramm pro Liter (kg/L)

Schritte zur Berechnung der Dichte

Masse messen:
- Bestimme die Masse des Objekts mithilfe einer Waage. Stelle sicher, dass die Messung in Kilogramm (kg) erfolgt.
Volumen messen:
- Bestimme das Volumen des Objekts. Bei regelmäßigen geometrischen Formen wie Würfeln oder Zylindern kannst du mathematische Formeln anwenden, um das Volumen zu berechnen. Bei unregelmäßigen Formen kannst du das Verdrängungsverfahren verwenden.
Formel anwenden:
- Berechne die Dichte mit der Formel: $\rho = \frac{m}{V}$

Dichteanomalie

Grundprinzipien

Definition: Eine Dichteanomalie tritt auf, wenn ein Material unter bestimmten Bedingungen eine unerwartete Veränderung der Dichte zeigt. Das bekannteste Beispiel ist die Dichteanomalie des Wassers.
Wasserspezifische Dichteanomalie:
- Wasser hat bei $4^{\circ} C$ seine höchste Dichte $\approx 1 \frac{g}{cm^3}$ .
- Oberhalb und unterhalb dieser Temperatur nimmt die Dichte ab, was dazu führt, dass Eis auf Wasser schwimmt.

Ursachen der Dichteanomalie

Molekularstruktur:
- Die Struktur der Wassermoleküle und die Wasserstoffbrückenbindungen führen zu einer ungewöhnlichen Anordnung der Moleküle im festen Zustand (Eis), was zu einer geringeren Dichte als im flüssigen Zustand führt.
Temperaturabhängigkeit:
- Bei Temperaturen unter $4^{\circ} C$ beginnen die Wassermoleküle, sich in eine offene hexagonale Struktur zu ordnen, was mehr Raum zwischen den Molekülen lässt und somit die Dichte verringert.

Auswirkungen der Dichteanomalie

Ökologische Bedeutung:
- Die Dichteanomalie des Wassers spielt eine entscheidende Rolle im Überleben von aquatischen Ökosystemen. Da Eis auf der Wasseroberfläche schwimmt, bleibt darunterliegendes Wasser bei Temperaturen oberhalb des Gefrierpunkts, was das Überleben von Wasserlebewesen im Winter ermöglicht.
Technische Anwendungen:
- Die Dichteanomalie von Wasser wird in der Klimaforschung, Hydrologie und bei der Entwicklung von Kühlsystemen berücksichtigt.

Die Dichte eines Körpers ( $\rho$ , geschrieben: rho) ist der Bruch aus seiner Masse $m$ und seinem Volumen $V$ :

Dichte

$\rho = \dfrac{m}{V}$

Die Dichte ist eine charakteristische Eigenschaft eines Körpers und unabhängig von seiner Form und seiner Größe. Die Dichte wird also über die Masse und das Volumen eines Körpers bestimmt.

Die abgleitete SI-Einheit der Dichte ist kg/m³. Häufig wird die Dichte aber nicht in dieser Einheit angegeben, sondern in g/cm³ und kg/l. Es ist also eher unüblich die Dichte in ihrer abgeleiteten SI-Einheit anzugeben. Für weiterführende Berechnungen, in denen die Dichte vorkommt, solltest du aber die Dichte in jedem Fall in die abgeleitete SI-Einheit kg/m³ umrechnen. Wie das funktioniert haben wir dir bereits in der vorangegangenen Lerneinheit (Einheiten umrechnen) gezeigt.

Beispiel: Dichte vergleichen

Beispiel!

Das kannst du dir ganz einfach vorstellen, wenn jeweils eine Hand mit Steinen und eine Hand mit Watte füllst. Du hast nun dasselbe Volumen (deine Hand), aber ein unterschiedliches Gewicht. Die Steine sind in deiner Hand schwerer als die Watte, demnach ist die Masse der Steine größer, als die Masse der Watte.

$\rho_{stein} = \dfrac{m_{Stein}}{V}$

$\rho_{Watte} = \dfrac{m_{Watte}}{V}$

Wenn du dir nun die obigen Gleichungen anschaust und $V = const$ ist, sich also nicht ändert, dann muss die Dichte der Steine größer sein, als die Dichte der Watte.

Temperatur und Dichte

Bei einer bestimmten Temperatur und einem bestimmten Druck besitzt jeder Stoff eine bestimmte Dichte. Die Angaben zur Dichte eines Stoffs bezieht sich deshalb immer auf bestimmte Temperaturen (0 °C, 20 °C, 25 °C) und den Normdruck (1013, 25 mbar bzw. 101, 325 kPa).

Wird nun ein fester oder flüssiger Stoff erwärmt, so dehnt sich der Körper aus und vergrößert damit sein Volumen. Steigt das Volumen, so sinkt die Dichte. Sinkt die Temperatur wieder, so zieht sich der Körper wieder zusammen, das Volumen wird kleiner und die Dichte steigt.

Merk’s dir!

Im Allgemeinen dehnen sich feste und flüssige Stoffe mit steigender Temperatur aus, sodass ihre Dichte dabei sinkt. Gasförmige Stoffe dehnen sich besonders stark aus, wenn sie nicht in einem starren Gefäß eingeschlossen sind.

In der nachfolgenden Grafik siehst du nochmal welchen Einfluss die Änderung der Masse (bei gleichbleibendem Volumen) und welchen Einfluss die Änderung des Volumens (bei gleichbleibender Masse) auf die Dichte hat:

Dichte - Gleichungen für gleichbleibendes Volumen und gleichbleibende Masse — Dichte – Gleichungen für gleichbleibendes Volumen und gleichbleibende Masse

Steigt (sinkt) also die Masse bei gleichbleibendem Volumen, so steigt (sinkt) auch die Dichte. Steigt (sinkt) das Volumen bei gleichbleibender Masse, so sinkt (steigt) die Dichte.

Beispiel: Dichte von Milch

Beispiel!

Du kannst die obige Formel zur Bestimmung der Dichte anwenden, wenn du zwei der drei Größen gegeben hast. Hast du hingegen keine Größe gegeben und du willst die Dichte einer Flüssigkeit bestimmen, dann kannst du diese zuhause ermitteln. Stell dir vor willst die Dichte von Milch bestimmen.

Dazu nimmst du dir einen Messbecher und wiegst diesen auf einer Küchenwaage. Drück die TARA Taste, damit das Gewicht des Messbechers nicht mitberücksichtigt wird. Schütte dann Milch in den Messbecher. Dabei ist es egal, ob du nun 100 ml oder 500 ml in den Messbecher kippst. Das ist das Volumen, welches die Milch einnimmt. Sagen wir mal du schüttest 100 ml in den Messbecher. Dies entspricht:

$100 ml = 0,1 l = 0,1 dm^3$

$0,1 dm^3 = 0,1 \cdot 0,001 dm^3 = 0,0001 m^3$

Die Waage zeigt dir nun zu dem eingeschütteten Volumen das zugehörige Gewicht der Milch an. Dies ist die Masse in Gramm oder Kilogramm (je nachdem was du auf der Waage eingestellt hast). Du kannst nun die Berechnung durchführen, indem du die Masse durch das Volumen teilst. Hast du Kuhmilch verwendet, sollte die Dichte zwischen 1.028 kg/m³ und 1.035 kg/m³ liegen.

Im Video oben ist die Dichte nicht in der abgeleiteten SI-Einheit kg/m³ angegeben. Wenn du die Dichte aber für weitere Berechnungen innerhalb einer Gleichung benötigst, solltest du diese zunächst in die SI-Einheit umrechnen. Soll lediglich die Dichte angegeben werden, so kannst du diese auch in anderen Einheiten wie g/cm³ oder kg/l angeben.

Die Umrechnung der obigen Einheiten in die abgeleitete SI-Einheit wird wie folgt vorgenommen:

Umrechnung

Beispiel 1:

$2,7 \dfrac{g}{cm^3} = 2,7 \dfrac{0,001}{1 \cdot 10^{-6}} \dfrac{ kg}{m^3} = 2,7 \cdot 1.000 \dfrac{ kg}{m^3} = 2.700 \dfrac{ kg}{m^3}$

Beispiel 2:

$0,997 \dfrac{g}{cm^3} = 0,997 \dfrac{0,001}{1 \cdot 10^{-6}} \dfrac{ kg}{m^3} = 0,997 \cdot 1.000 \dfrac{ kg}{m^3} = 997 \dfrac{ kg}{m^3}$

Videoclip: Eisendraht mit kreisförmigen Querschnitt

In einem weiteren Video zeigt dir Jessica, wie du die Länge eines Eisendrahtes mit kreisförmigen Querschnitt aus der gegebenen Dichte berechnen kannst:

Lernclip: Länge aus der Dichte bestimmen

Dichteanomalie von Wasser

Wir haben haben beschrieben, dass sich ein fester oder flüssiger Stoff mit zunehmender Temperatur ausdehnt und mit sinkender Temperatur zusammenzieht. Im ersteren Fall steigt die Dichte, im letzteren Fall sinkt die Dichte. Es gibt aber auch Stoffe die sich nicht so verhalten. Man spricht in einem solchen Fall von einer Dichteanomalie. Das bekannteste Beispiel für die Dichteanomalie eines Stoffes ist Wasser.

Wasser hat eine ganz besondere Eigenschaft, die keine andere Flüssigkeit hat:

Wird Wasser abgekühlt, so verringert es zunächst sein Volumen und damit steigt auch seine Dichte. Bei 4 Grad Celsius ist das Volumen des Wassers am kleinsten und damit die Dichte der Teilchen am größten.

Bis jetzt noch alles wie oben beschrieben. Aber was passiert, wenn das Wasser unter 4°C abgekühlt wird?

Fällt die Temperatur des Wasser unter 4°C, so dehnt sich das Wasser wieder aus! Das Volumen nimmt also zu und damit nimmt die Dichte ab. Das ist auch der Grund dafür, warum Eis auf dem Wasser schwimmt. Das Eis besitzt eine Temperatur unter 0°C und besitzt damit eine größere Dichte als Wasser, welches eine größere Temperatur aufweist.

Think about your drink!

Du kennst das sicherlich auch aus dem Alltag. Deine Freunde wollen vorbei kommen und du hast mal wieder vergessen das Bier kalt zu stellen. Ist doch wohl klar, dass du das Bier in die Tiefkühltruhe legst, damit das Bier auch rechtzeitig kühl ist und ihr nicht mit ner warmen Plörre anstoßen müsst. Aber wie das so ist, vergisst du eine Bierflasche in der Tiefkühltruhe. Tage später entdeckst du die zerplatzte Bierflasche und denkst natürlich sofort an die Dichteanomalie von Wasser (ja auch in Bier ist Wasser drin). Da die Bierflasche ein festes Volumen aufweist (sie ist zu) und Wasser sich bei Temperaturen unter 4°C wieder ausdehnt, hat sich die Flüssigkeit eben selbst ihren Platz geschaffen.

Die Dichteanomalie von Wasser ist ebenfalls verantwortlich dafür, dass du im Winter Frostschutzmittel in den Kühler deines Autos füllen musst. Denn ansonsten würde das Wasser dort anfangen zu frieren und sich auszudehnen. Das würde zum Platzen deines Kühlers führen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist Dichte?

Dichte ist die Masse eines Stoffes pro Volumeneinheit und wird in kg/m³ gemessen.

2. Wie berechnet man die Dichte?

Die Dichte wird berechnet, indem man die Masse durch das Volumen teilt: $\rho = \frac{m}{V}$

3. Warum ist Dichte wichtig?

Dichte hilft bei der Identifikation von Materialien, der Berechnung von Tragfähigkeiten und der Vorhersage von Naturphänomenen.

4. Wie beeinflussen Temperatur und Druck die Dichte?

Mit steigender Temperatur nimmt die Dichte ab, da sich das Volumen vergrößert. Mit steigendem Druck nimmt die Dichte zu, da sich das Volumen verkleinert.

5. Was ist die Dichteanomalie des Wassers?

Wasser hat bei 4°C seine höchste Dichte, was dazu führt, dass Eis auf Wasser schwimmt und das Überleben von Wasserlebewesen im Winter ermöglicht.

Zusammenfassung

Die Dichte und die Dichteanomalie sind fundamentale Konzepte in der Physik und Chemie. Die Dichte beschreibt die Masse eines Materials pro Volumeneinheit, während die Dichteanomalie ungewöhnliche Veränderungen der Dichte unter bestimmten Bedingungen erklärt.

Ein bekanntes Beispiel ist die Dichteanomalie des Wassers, die eine entscheidende Rolle in ökologischen Systemen spielt. Das Verständnis dieser Konzepte ist wichtig für Anwendungen in Wissenschaft und Technik, von der Materialwissenschaft bis hin zur Ökologie.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie der Druck bestimmt wird.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++