PH1 – Beispiel zum Kosinussatz und Sinussatz

In der Lerneinheit Kosinussatz und Sinussatz zeigen wir dir ein Berechnungsbeispiel auf, in welchen du beide Verfahren benötigst.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Physik findest du im Kurs: PH1 – Grundlagen der Physik.

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Kosinussatz und Sinussatz – Grundlagen

Was sind der Kosinussatz und Sinussatz?

Der Kosinussatz und der Sinussatz sind zentrale Theoreme in der Trigonometrie, die zur Lösung von allgemeinen Dreiecken verwendet werden. Diese Sätze sind besonders nützlich, wenn es darum geht, Seitenlängen und Winkel in nicht-rechtwinkligen Dreiecken zu bestimmen.

Häufig tritt der Fall auf, dass bei Berechnungen an dreieckigen Flächen beide Sätze angewendet werden müssen. Wir wollen uns in dieser Lerneinheit mal diesen Fall genauer anschauen.

Du benötigst hierfür die folgenden Gleichungen.

Formeln: Kosinussatz und Sinussatz

Kosinussatz

Berechnung von Seiten

$c = \sqrt{a^2 + b^2 - 2 \cdot a \cdot b \cdot \cos(\gamma)}$

$a = \sqrt{b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(\alpha)}$

$b = \sqrt{a^2 + c^2 - 2 \cdot a \cdot c \cdot \cos(\beta)}$

Berechnung von Winkel

$\gamma = \cos^{-1}(\dfrac{a^2 + b^2 - c^2 }{2 \cdot a \cdot b})$

$\alpha = \cos^{-1}(\dfrac{b^2 + c^2 - a^2 }{2 \cdot b \cdot c})$

$\beta = cos^{-1}(\dfrac{a^2 + c^2 - b^2 }{2 \cdot a \cdot c})$

Sinussatz

$\dfrac{a}{\sin(\alpha)} = \dfrac{b}{\sin(\beta)} = \dfrac{c}{\sin(\gamma)}$

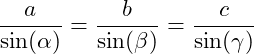
Beispiel: Sätze

Schauen wir uns mal ein Beispiel zur Berechnung einer Aufgabe an, in welcher beide Sätze benötigt werden.

Beispiel!

Kosinussatz Sinussatz - Anwenden — Kosinussatz und Sinussatz – Anwenden

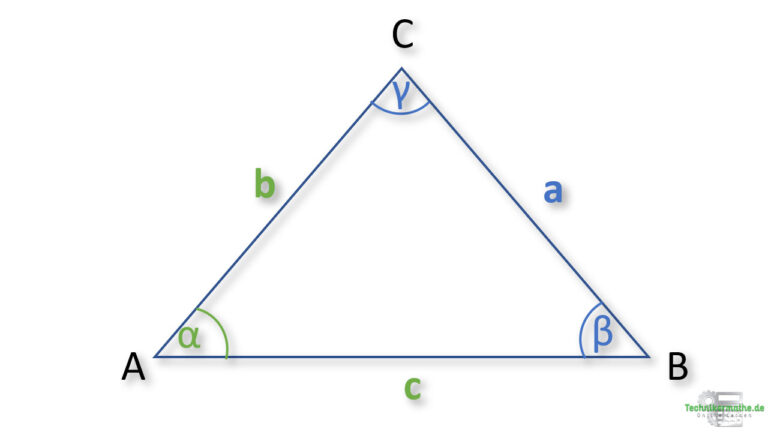
Gegeben sei das allgemeine Dreieck mit dem Winkel α = 60° und den Seiten b = 4cm und c = 8cm.

Berechne den Winkel β.

Wir haben zwar zwei Seiten und ein Winkel gegeben, da die gegenüberliegenden Winkel der gegebenen Seiten aber beide unbekannt sind, kann hier die Berechnung mit dem Sinussatz zunächst nicht erfolgen. Wir haben den Winkel α gegeben und können mittels Kosinussatz die Seite a berechnen. Danach können wir dann den Sinussatz anwenden, um den Winkel β zu bestimmen.

Der Kosinussatz lautet:

$a = \sqrt{b^2 + c^2 - 2 \cdot b \cdot c \cdot \cos(\alpha)}$

Danach kannst du die in der Aufgabenstellung gegebenen Werte eingeben:

$a = \sqrt{(4cm)^2 + (8cm)^2 - 2 \cdot 4cm \cdot 8cm \cdot \cos(60^\circ)} = 6,93 cm$

Nachdem wir die Seite a berechnet haben und der gegenüberliegenden Winkel α gegeben ist, können wir den Winkel β mittels Sinussatz bestimmen:

$\dfrac{a}{\sin(\alpha)} = \dfrac{b}{\sin(\beta)}$

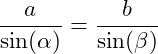
Jetzt löst du die obigen Gleichung nach dem dem Winkel β auf:

$\beta = \sin^{-1} (\dfrac{\sin(\alpha)}{a} \cdot b)$

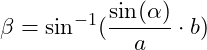
Im letzten Schritt setzt du die gegebenen Werte ein:

$\beta = \sin^{-1} (\dfrac{\sin(60^\circ)}{6,93 cm} \cdot 4 cm) = 29,99 cm \approx 30 cm$

Anwendung der Sätze

Navigation und Geodäsie: Bestimmen von Positionen und Entfernungen.
Ingenieurwesen: Berechnung von Kräften und Spannungen in Strukturen.
Astronomie: Berechnung von Winkeln und Entfernungen zwischen Himmelskörpern.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist der Kosinussatz?

Der Satz ist eine Verallgemeinerung des Satzes des Pythagoras für beliebige Dreiecke.

2. Wann verwendet man den Sinussatz?

Der Satz wird verwendet, wenn zwei Winkel und eine Seite oder zwei Seiten und ein nicht-eingeschlossener Winkel bekannt sind.

3. Kann man den Kosinussatz bei rechtwinkligen Dreiecken anwenden?

Ja, der Satz vereinfacht sich zum Satz des Pythagoras bei rechtwinkligen Dreiecken.

4. Was ist der Unterschied zwischen dem Sinussatz und dem Kosinussatz?

Der Sinussatz beschreibt das Verhältnis von Seitenlängen zu den Sinuswerten ihrer gegenüberliegenden Winkel, während der Kosinussatz eine Beziehung zwischen allen drei Seitenlängen und einem Winkel herstellt.

5. Gibt es Einschränkungen für die Anwendung des Sinussatzes?

Ja, der Satz kann mehrdeutige Lösungen liefern, wenn zwei mögliche Winkel den gleichen Sinuswert haben.

Zusammenfassung

Die Sätze sind essenzielle Werkzeuge in der Trigonometrie, die zur Lösung von Dreiecken verwendet werden. Der Kosinussatz erweitert den Satz des Pythagoras auf beliebige Dreiecke und ermöglicht die Berechnung von Seiten und Winkeln.

Der Sinussatz beschreibt das Verhältnis der Seitenlängen zu den Sinuswerten ihrer gegenüberliegenden Winkel und hilft ebenfalls bei der Lösung von Dreiecken. Beide Sätze haben breite Anwendungen in verschiedenen wissenschaftlichen und technischen Bereichen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++