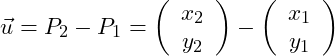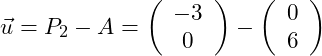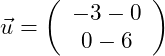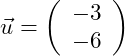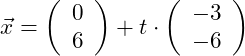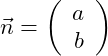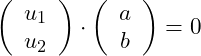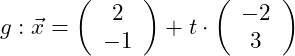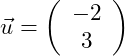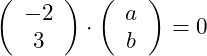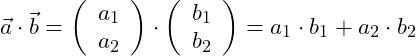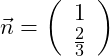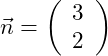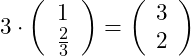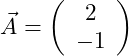MA4 – Koordinatenform in Parameterform und umgekehrt

In dieser Lerneinheit wollen wir uns anschauen, wie wir die Gleichung einer Geraden in der Ebene von der Parameterform in Koordinatenform und Koordinatenform in Parameterform umwandeln.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: MA4 – Vektorrechnung

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Koordinatenform in Parameterform umwandeln | Grundlagen

In dieser Lerneinheit behandeln Geraden in der Ebene und wollen dir zeigen, wie du die Parameterform einer Gerade in die Koordinatenform umwandelst und umgekehrt. Wir zeigen dir welche Formeln du benötigst und zeigen dir das Vorgehen an zwei Beispielen auf.

Koordinatenform in Parameterform? Detaillierte Anleitung und Anwendung

Die Umwandlung der Koordinatenform einer Ebene in die Parameterform ist ein wesentlicher Schritt in der analytischen Geometrie. Diese Transformation ermöglicht eine bessere Visualisierung und Analyse der Ebene im dreidimensionalen Raum, insbesondere bei der Untersuchung von Geraden und Flächen. Hier erfährst du, wie du die Koordinatenform in die Parameterform umwandelst und welche praktischen Anwendungen diese Formen haben.

Übersicht der Gleichungen

Formeln

Koordinatenform

$ax + bx = c$

Parameterform

$\vec{x} = \vec{A} + t \cdot \vec{u}$

Koordinatenform in Parameterform umwandeln

Ist eine Gerade in Koordinatenform gegeben und du sollst diese in Parameterform umwandeln, dann musst du die folgenden Schritte ausführen:

1.Zwei Punkte auf der Geraden suchen, indem wir für x und y Werte einsetzen. Das geht zum Beispiel, indem wir die Schnittpunkte betrachten, also einmal x = 0 setzen und die Koordinatenform nach y auflösen und einmal y = 0 setzen und nach x auflösen. Dann haben wir die Schnittpunkte mit den Achsen gegeben.

2.Einer der Punkte P₁ (x₁|y₁) wird als Aufpunkt des Ortsvektors gewählt. Von diesem Punkt ausgehend, bewegen wir uns zum zweiten Punkt P₂(x₂|y₂). Dazu berechnen wir den Abstand zwischen den beiden Punkten, indem wir beide subtrahieren. Dieser Abstand ist nichts anderes als unser Richtungsvektor $\vec{u}$ :

$\vec{u} = P_2 - P_1 = \left( \begin{array}{c} x_2 \\ y_2 \end{array}\right) - \left( \begin{array}{c} x_1 \\ y_1 \end{array}\right)$

Schauen wir uns dazu ein Beispiel an.

Beispiel: Koordinatenform in Parameterform

Beispiel!

Gegeben sei die folgende Gerade in Koordinatenform:

$-4x + 2y = 12$

Wie lautet die Parameterform der Geraden?

1.Wir suchen zunächst zwei Punkte auf der Geraden. Du kannst nun Werte für x und y so einsetzen, dass 12 reultiert, so dass die Gleichung erfüllt ist. Oder du setzt für x = 0 ein und löst nach y auf. So hast du den Schnittpunkt der Geraden mit der y-Achse ermittelt:

$-4 \cdot 0 + 2y = 12$

$2y = 12$

$y = 6$

Wir haben den ersten Punkt gegeben mit:

$P_1(0|6)$

Für den zweiten Punkt setzen wir y = 0 und lösen nach x auf, so haben wir den Schnittpunkt der Geraden mit der x-Achse gegeben:

$-4x + 2 \cdot 0 = 12$

$-4x = 12$

$x = -3$

$P_2(-3|0)$

2.Wir haben einfach zwei Punkte auf der Geraden ermittelt. Einen der Punkte wählen wir als Aufpunkt (z.B. P₁ = A). Dann müssen wir diesen Aufpunkt von dem zweiten Punkt subtrahieren:

$\vec{u} = P_2 - A = \left( \begin{array}{c} -3 \\ 0 \end{array}\right) - \left( \begin{array}{c} 0 \\ 6 \end{array}\right)$

$\vec{u} = \left( \begin{array}{c} -3 - 0 \\ 0 - 6 \end{array}\right)$

$\vec{u} = \left( \begin{array}{c} -3 \\ -6 \end{array}\right)$

Wir können jetzt die Parameterform aufstellen:

$\vec{x} = \vec{A} + t \cdot \vec{u}$

$\vec{x} = \left( \begin{array}{c} 0 \\ 6 \end{array}\right) + t \cdot \left( \begin{array}{c} -3 \\ -6 \end{array}\right)$

In der folgenden Grafik siehst du die Gerade eingezeichnet:

Parameterform, Koordinatenform, umwandeln, Gerade in der Ebene, Koordinatenform in Parameterform — Koordinatenform in Parameterform

Parameterform in Koordinatenform umwandeln | Grundlagen

Parameterform in Koordinatenform? Detaillierte Anleitung und Anwendung

Die Umwandlung der Parameterform einer Ebene in die Koordinatenform ist ein wesentlicher Schritt in der analytischen Geometrie. Diese Transformation ermöglicht eine präzisere algebraische Darstellung der Ebene und erleichtert viele Berechnungen, wie zum Beispiel die Bestimmung von Schnittpunkten.

Um die gegebene Parameterform einer Geraden in Koordinatenform umwandeln zu können, betrachten wir den Richtungsvektor $\vec{u}$ der Parameterform und bilden den dazugehörigen Normalenvektor $\vec{n}$ , also denjenigen Vektor, der senkrecht auf dem Richtungsvektor steht.

Vorgehensweise:

$\vec{n} = \left( \begin{array}{c} a \\ b \end{array}\right)$

Dieser Normalenvektor steht senkrecht auf den Richtungsvektor. Zwei Vektoren stehen senkrecht zueinander, wenn das Skalarprodukt Null ergibt:

$\vec{u} \cdot \vec{n} = 0$

Wir bilden das Skalarprodukt:

$\left( \begin{array}{c} u_1 \\ u_2 \end{array}\right) \cdot \left( \begin{array}{c} a \\ b \end{array}\right) = 0$

$u_1 \cdot a + u_2 \cdot b = 0$

Wir setzen nun für a einen bliebigen Wert ein und berechnen b. Die ermittelten Koordinaten des Normalenvektors sind die Koeffizienten a und b innerhalb der Koordinatenform:

$ax + bx = c$

Um nun c zu ermitteln, setzen wir für x und y die Koordinaten des Aufpunktes ein.

Betrachten wir hierzu mal ein Beispiel.

Beispiel: Parameterform in Koordinatenform

Beispiel!

Gegeben sei die folgende Gerade in Parameterform:

$g: \vec{x} = \left( \begin{array}{c} 2\\ -1 \end{array}\right) + t \cdot \left( \begin{array}{c} -2 \\ 3 \end{array}\right)$

Bestimmte die Koordinatenform der Geraden!

Im ersten Schritt suchen wir den Vektor, der senkrecht auf dem Richtungsvektor $\vec{u}$ steht. Hierbei handelt es sich um den Normalenvektor $\vec{n}$ .

Der Richtungsvektor in unserem Beispiel lautet:

$\vec{u} = \left( \begin{array}{c} -2 \\ 3 \end{array}\right)$

Der Normalenvektor weist als Koordinaten die Koeffizienten der Koordinatenform auf, weshalb wir ihn wie folgt definieren:

$\vec{n} = \left( \begin{array}{c} a \\ b \end{array}\right)$

Zwei Vektoren stehen dann senkrecht aufeinander, wenn ihr Skalarprodukt Null ergibt. Damit müssen wir das Skalarprodukt aus beiden Vektoren gleich Null setzen:

$\vec{u} \cdot \vec{n} = 0$

$\left( \begin{array}{c} -2 \\ 3 \end{array}\right) \cdot \left( \begin{array}{c} a \\ b \end{array}\right) = 0$

Wiederholung Skalarprodukt (Ebene)

$\vec{a} \cdot \vec{b} = \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \cdot \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) = a_1 \cdot b_1 + a_2 \cdot b_2$

Wir berechnen das Skalarprodukt:

$-2 \cdot a + 3 \cdot b = 0$

$-2a + 3b = 0$

Wir suchen noch immer den Normalenvektor. Um diesen zu ermitteln, müssen wir für a oder b eine beliebige Zahl einsetzen und die andere Variable berechnen. Setzen wir also zum Beispiel für a = 1 ein, so erhalten wir:

$-2 \cdot 1 + 3b = 0$

$b = \frac{2}{3}$

Damit lautet unser Normalenvektor:

$\vec{n} = \left( \begin{array}{c} 1 \\ \frac{2}{3} \end{array}\right)$

Wir können auch andere beliebige Werte einsetzen und die Gleichung lösen, so zum Beispiel b = 2:

$-2a + 3 \cdot 2 = 0$

$a = 3$

Wir erhalten damit den Normalenvektor:

$\vec{n} = \left( \begin{array}{c} 3 \\ 2 \end{array}\right)$

Es gibt unendlich viele Normalenvektoren, die wir hier ermitteln können. Alle diese Normalenvektoren sind Vielfache voneinander:

$3 \cdot \left( \begin{array}{c} 1 \\ \frac{2}{3} \end{array}\right) = \left( \begin{array}{c} 3 \\ 2 \end{array}\right)$

Damit erhalten wir immer den Normalenvektor, egal welche Werte wir für a oder b einsetzen. Wir entscheiden uns hier für den folgenden Normalenvektor:

$\vec{n} = \left( \begin{array}{c} 3 \\ 2 \end{array}\right)$

Der Grund liegt darin, dass wir diesen Normalenvektor besser einzeichnen können, da 2/3 schwieriger in ein Koordinatensystem einzuzeichnen ist. Musst du keine Zeichnung der Geraden und des Normalenvektors vornehmen, so kannst du den Normalenvektor auch mit 2/3 verwenden.

Nachdem wir nun den Normalenvektor ermittelt haben, können wir die Koordinatenform aufstellen, denn a = 3 und b = 2:

$3x + 2y = c$

Im letzten Schritt benötigen wir den Aufpunkt des Ortsvektors, um c zu berechnen. Der Aufpunkt in unserem Beispiel lautet:

$\vec{A} = \left( \begin{array}{c} 2\\ -1 \end{array}\right)$

Dazu setzen wir diesen Aufpunkt in die Koordinatenform ein und berechnen c:

$3 \cdot 2 + 2 \cdot (-1) = c$

$6 - 2 = c$

$c = 4$

Wir erhalten am Ende die folgende Koordinatenform:

$3x + 2y = 4$

In der folgenden Grafik siehst du die Gerade sowie den ermittelten Normalenvektor eingezeichnet:

Normalenvektor, Koordinatenform, Parameterform, Steigungsform, Gerade in der Ebene, Parameterform in Koordinatenform — Parameterform in Koordinatenform

Anwendung in der Praxis

Ingenieurwesen: Analyse von Strukturen und Bauwerken.
Physik: Untersuchung von Ebenen und Kräften in der Raummechanik.
Computergraphik: Modellierung und Rendering von 3D-Oberflächen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist die Koordinatenform einer Ebene?

Diese Form ist eine Gleichung der Form $ax + bx = c$ , die eine Ebene im dreidimensionalen Raum beschreibt.

2. Was ist die Parameterform einer Ebene?

Diese Form ist eine Darstellung der Form $\vec{x} = \vec{A} + t \cdot \vec{u}$ , bei der $\vec{A}$ ein Punkt auf der Ebene und $\vec{u}$ ein Richtungsvektor ist.

3. Wie wandle ich die Koordinatenform in die Parameterform um?

Bestimme einen Punkt $\vec{A}$ auf der Ebene. Finde einen Richtungsvektor $\vec{u}$ , der in der Ebene liegt. Stell dann die Parameterform $\vec{x} = \vec{A} + t \cdot \vec{u}$ auf.

4. Wofür wird die Parameterform verwendet?

Die Parameterform wird verwendet, um die Ebene anschaulich darzustellen und Berechnungen im Raum zu vereinfachen.

5. Was sind Richtungsvektoren?

Richtungsvektoren sind Vektoren, die die Richtung innerhalb der Ebene angeben und linear unabhängig voneinander sein müssen.

Zusammenfassung

Die Bestimmung der S-Punkte einer Geraden im Raum erfordert die Analyse der Parametergleichung und das Setzen der Koordinaten gleich null, um die Schnittpunkte mit den Koordinatenebenen zu finden.

Diese Methode ist in der analytischen Geometrie, im Ingenieurwesen und in der Physik von großer Bedeutung und hilft, die Lage und Orientierung von Geraden im dreidimensionalen Raum präzise zu bestimmen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++