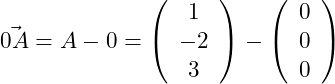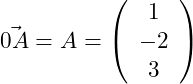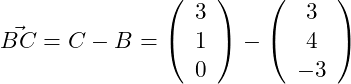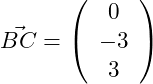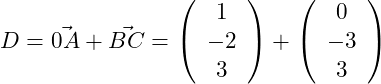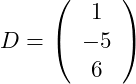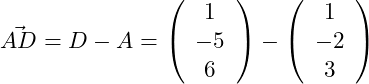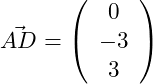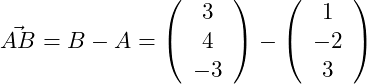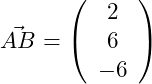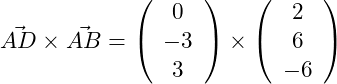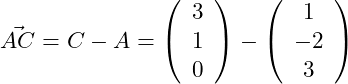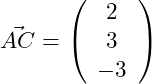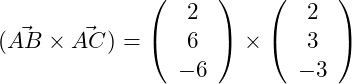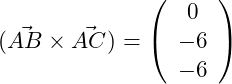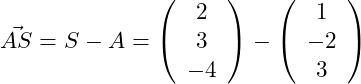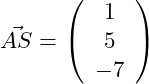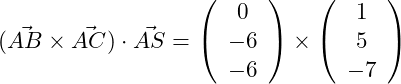MA4 – Prüfungsaufgabe 1: Volumen und Fläche aus gegebenen Punkten

Wir können das Volumen aus Punkten berechnen. Sind 4 Punkte gegeben, so können wir das Volumen von Körpern aus dem Spatprodukt bestimmen. Außerdem können wir aus 3 Punkten die Fläche von Körpern berechnen. In dieser Lerneinheit betrachten wir die Flächen von Parallelogramm und Dreieck sowie die Volumina von Spat und Pyramide.

In dieser Lerneinheit schauen wir uns eine ausführliche Aufgabe zur Anwendung des Vektor- und Spatprodukts an. Dabei wollen wir die Koordinaten eines Punktes bestimmen, den Flächeninhalt eines Dreiecks und Parallelogramms berechnen sowie das Volumen einer Pyramide.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs MA4 – Vektorrechnung auf Technikermathe.de

Für ein optimales Verständnis hilft dir ein anschauliches Rechenbeispiel zu dem Thema.

Aufgabe zum Vektor- und Spatprodukt

Gegeben sind die Punkte A(1|-2|3), B(3|4|-3), C(3|1|0) und S(2|3|-4).

a) Das Dreieck ABC lässt sich zu einem Parallelogramm ABCD ergänzen. Bestimme die Koordinaten von D und berechne den Flächeninhalt dieses Parallelogramms.

b) Berechne den Flächeninhalt des Dreiecks ABC.

c) Berechne das Volumen des Spats, der von den drei Vektoren $\vec{AB}$ , $\vec{AC}$ und $\vec{AS}$ aufgespannt wird.

d) Berechne das Volumen der Pyramide ABCS.

Lösung zur Aufgabe

Lösung a) Koordinaten von D + Flächeninhalt

Wir skizzieren (zur besseren Übersicht) zunächst ein Parallelogramm aus den vier Punkten A, B, C und D, wobei D nicht gegeben ist:

Wir zeichnen das Parallelogramm so ein, dass wir die mathematisch korrekte Reihenfolge der Punkte wählen. Die Eckpunkte des Parallelogramms werden in aufsteigender alphabetischer Reihenfolge (A,B,C,D) gegen den Uhrzeigersinn eingezeichnet (siehe Grafik). Wir beginnen also mit dem Punkt A und gehen dann gegen dem Uhrzeigersinn zum Punkt B usw.

Wir suchen die Koordinaten des Punktes D. Der kürzeste Weg, um zum Punkt D zu gelangen, ist die Strecke AD. Wir starten also im Punkt A und gehen dann zum Punkt D. Da wir die Koordinaten des Punktes D suchen, müssen wir hier mit Vektoren rechnen. In der nachfolgenden Grafik sind die Vektoren eingezeichnet, die wir zur Berechnung benötigen:

Die obige Grafik dient lediglich als Skizze und zeigt ein Parallelogramm (ABCD) in einem x,y,z-Koordinatensystem. Wir suchen die Koordinaten von Punkt D. Dazu starten wir im Koordinatenursprung und bewegen uns zum Punkt A. Wir haben hier den ersten Vektor gegeben $\vec{0A}$ . Danach bewegen wir uns vom Punkt A zum Punkt D. Dies entspricht dem Vektor $\vec{AD}$ . Da die gegenüberliegenden Seiten in einem Parallelogramm identisch sind, ist der Vektor $\vec{AD}$ identisch mit dem Vektor $\vec{BC}$ .

Wir erhalten also:

$D = \vec{0A} + \vec{AD}$

Und da $\vec{AD} = \vec{BC}$ gilt:

$D = \vec{0A} + \vec{BC}$

Zunächst benötigen wir nun den Vektor $\vec{0A}$ . Dies ist ein Ortsvektor, der im Koordinatenursprung beginnt und auf den Punkt A zeigt. Dieser Vektor ist identisch mit dem Punkt A. Zur Berechnung des Abstands zweier Punkte in Koordinatendarstellung, wird der Anfangspunkt von dem Endpunkt abgezogen. Hier also:

$\vec{0A} = A - 0 = \left( \begin{array}{c} 1 \\ -2\\ 3 \end{array} \right) - \left( \begin{array}{c} 0 \\ 0 \\ 0 \end{array} \right)$

$\vec{0A} = A = \left( \begin{array}{c} 1 \\ -2\\ 3 \end{array} \right)$

Für Ortsvektoren gilt immer, dass die Koordinaten des Ortsvektors mit dem Punkt, auf welchen der Ortsvektor zeigt übereinstimmen.

Wir benötigen noch den Richtungsvektor $\vec{BC}$ :

$\vec{BC} = C - B = \left( \begin{array}{c} 3 \\ 1\\ 0 \end{array} \right) - \left( \begin{array}{c} 3 \\ 4 \\ -3 \end{array} \right)$

$\vec{BC} = \left( \begin{array}{c} 0 \\ -3 \\ 3 \end{array} \right)$

Wir können jetzt die Koordinaten des Punktes D berechnen:

$D = \vec{0A} + \vec{BC} = \left( \begin{array}{c} 1 \\ -2\\ 3 \end{array} \right) + \left( \begin{array}{c} 0 \\ -3 \\ 3 \end{array} \right)$

$D = \left( \begin{array}{c} 1 \\ -5 \\ 6 \end{array} \right)$

Wir haben die Koordinaten des Punktes D berechnet.

Wir können D auch berechnen, indem wir den längeren Weg wählen:

$D = A + \vec{AB} + \vec{BC} + \vec{CD}$

Und da $\vec{CD} = \vec{AB}$ gilt:

$D = A + \vec{AB} + \vec{BC} + \vec{AB}$

Wir sollen zudem den Flächeninhalt des Parallelogramms berechnen. Dazu berechnen wir das Vektorprodukt aus zwei Vektoren und berechnen die Länge dieses Vektorprodukts. Wir können hier beliebig zwei Vektoren wählen mit der Voraussetzung, dass beide Vektoren im gleichen Punkt beginnen. Wir wählen beliebig $\vec{AD}$ und $\vec{AB}$ (beide beginnen im Punkt A).

Wir berechnen zunächst das Vektorprodukt:

$\vec{AD} \times \vec{AB}$

Dazu müssen wir die Vektoren aber noch berechnen:

$\vec{AD} = D - A = \left( \begin{array}{c} 1 \\ -5 \\ 6 \end{array} \right) - \left( \begin{array}{c} 1 \\ -2\\ 3 \end{array} \right)$

$\vec{AD} = \left( \begin{array}{c} 0 \\ -3 \\ 3 \end{array} \right)$

$\vec{AB} = B - A = \left( \begin{array}{c} 3 \\ 4 \\ -3 \end{array} \right) - \left( \begin{array}{c} 1 \\ -2\\ 3 \end{array} \right)$

$\vec{AB} = \left( \begin{array}{c} 2 \\ 6 \\ -6 \end{array} \right)$

Wir können nun das Vektorprodukt berechnen:

$\vec{AD} \times \vec{AB} = \left( \begin{array}{c} 0 \\ -3 \\ 3 \end{array} \right) \times \left( \begin{array}{c} 2 \\ 6 \\ -6 \end{array} \right)$

In der obigen Grafik siehst du die Berechnung des Vektorprodukts. Nachdem wir das Vektorprodukt berechnet haben, benötigen wir die Länge des Vektorprodukts, um den Flächeninhalt des durch die beiden Vektoren aufgespannten Parallelogramms berechnen zu können:

$|\vec{AD} \times \vec{AB}| = \sqrt{0^2 + 6^2 + 6^2} = 6\sqrt{2}$

Wir haben den Flächeninhalt des Parallelogramms ABCD berechnet. Die Fläche beträgt 6√2 Flächeneinheiten.

Lösung b) Fläche eines Dreiecks ABC

Wir wollen nun den Flächeninhalt des Dreiecks ABC berechnen:

Den Flächeninhalt des Parallelogramms haben wir bereits berechnet. Teilen wir die Fläche durch 2, so erhalten wir genau die Fläche des gesuchten Dreiecks ABC:

$\frac{|\vec{AD} \times \vec{AB}|}{2} = \frac{1}{2} \sqrt{0^2 + 6^2 + 6^2} = 3\sqrt{2}$

Der Flächeninhalt des Dreiecks ABC beträgt 3√2 Flächeneinheiten.

Lösung c) Volumen des Spats | Spatprodukt

Wir wollen nun das Volumen des Spats berechnen. Ein Spat ist ein Körper, der aus Parallelogrammen zusammengesetzt ist. Ähnlich also wie ein Quader, nur dass die Seitenflächen keine Rechtecke, sondern Parallelogramme darstellen.

Das Spatprodukt berechnen wir immer aus drei Vektoren und wird wie folgt bestimmt:

$(\vec{AB} \times \vec{AC}) \cdot \vec{AS}$

Merk’s dir!

Sind in der Aufgabenstellung keine Vektoren, sondern Punkte gegeben, so ist es wichtig, dass alle Vektoren im gleichen Punkt beginnen. Hier wurde in der Aufgabenstellung der Anfangspunkt A gewählt.

Wir starten mit der Berechnung der Klammer, also mit der Berechnung des Vektorprodukts (bzw. Kreuzprodukts) aus den beiden Vektoren:

$(\vec{AB} \times \vec{AC})$

Wir benötigen noch die beiden Vektoren $\vec{AB}$ und $\vec{AC}$ . Den Vektor $\vec{AB}$ haben wir bereits im Aufgabenteil b) bestimmt:

$\vec{AB} = \left( \begin{array}{c} 2 \\ 6 \\ -6 \end{array} \right)$

Wir berechnen als nächstes den $\vec{AC}$ aus den beiden Punkten A und C:

$\vec{AC} = C - A = \left( \begin{array}{c} 3 \\ 1 \\ 0 \end{array} \right) - \left( \begin{array}{c} 1 \\ -2 \\ 3 \end{array} \right)$

$\vec{AC} = \left( \begin{array}{c} 2 \\ 3 \\ -3 \end{array} \right)$

Wir können jetzt das Vektorprodukt bestimmen:

$(\vec{AB} \times \vec{AC}) = \left( \begin{array}{c} 2 \\ 6 \\ -6 \end{array} \right) \times \left( \begin{array}{c} 2 \\ 3 \\ -3 \end{array} \right)$

In der folgenden Grafik siehst du die Berechnung des Vektorprodukts:

Wir erhalten demnach:

$(\vec{AB} \times \vec{AC}) = \left( \begin{array}{c} 0 \\ -6 \\ -6 \end{array} \right)$

Als nächstes berechnen wir das Skalarprodukt aus dem Vektorprodukt und dem Vektor $\vec{AS}$ :

$(\vec{AB} \times \vec{AC}) \cdot \vec{AS}$

Den Vektor $\vec{AS}$ müssen wir aber noch berechnen:

$\vec{AS} = S - A = \left( \begin{array}{c} 2 \\ 3 \\ -4 \end{array} \right) - \left( \begin{array}{c} 1 \\ -2 \\ 3 \end{array} \right)$

$\vec{AS} = \left( \begin{array}{c} 1 \\ 5 \\ -7 \end{array} \right)$

Wir können nun das Skalarprodukt aus dem Vektorprodukt und dem Vektor $\vec{AS}$ berechnen:

$(\vec{AB} \times \vec{AC}) \cdot \vec{AS} = \left( \begin{array}{c} 0 \\ -6 \\ -6 \end{array} \right) \times \left( \begin{array}{c} 1 \\ 5 \\ -7 \end{array} \right)$

$(\vec{AB} \times \vec{AC}) \cdot \vec{AS} = 0 \cdot 1 + (-6) \cdot 5 + (-6) \cdot (-7) = 12$

Hierbei handelt es sich um das Volumen des Spats mit 12 Volumeneinheiten.

Merk’s dir!

Ergibt sich ein negatives Ergebnis beim Spatprodukt, so wird der Betrag betrachtet. Das Spatprodukt ist damit immer positiv.

Lösung d) Volumen einer Pyramide ABCS

Wir wollen als nächstes die 4 Punkte A, B, C und S betrachten und daraus eine Pyramide konstruieren:

In der obigen Grafik haben wir aus den drei Punkten A, B und C die dreieckige Grundfläche der Pyramide erzeugt. Diese Fläche wird aus der Länge des Vektorprodukts wie folgt berechnet:

$A_D = \frac{1}{2} (|\vec{AB} \times \vec{AC}|)$

Wir suchen aber das Volumen einer Pyramide, welches wir über das Spatprodukt berechnen. Das Spatprodukt ermittelt das Volumen eines Spats. Das Volumen einer Pyramide ist genau 1/6 des Spatvolumens:

$V_{Py} = \frac{1}{6} (\vec{AB} \times \vec{AC}) \cdot \vec{AS}$

Wir haben bereits das Volumen des Spats in Aufgabenteil c) berechnet:

$(\vec{AB} \times \vec{AC}) \cdot \vec{AS} = 12$

Wir können nun direkt das Volumen der Pyramide bestimmen:

$V_{Py} = \frac{1}{6} \cdot 12 = 2$

Das Volumen der Pyramide beträgt 2 Volumeneinheiten.

Tausende interaktive Übungsaufgaben

Übungsbereich

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media)? Nein? – Dann schau einfach mal hinein:

Das erwartet dich!

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den >> kostenlosen Probekurs << durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Auszüge aus unserem Kursangebot!

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

building 4794329 1280 — TM1 (Technische Mechanik – Kurs)

scientist 6621069 1280 — WT3 (Werkstoffprüfung – Kurs)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Onlinekurs
++ Günstiger geht’s nicht!! ++

Oder direkt >> Mitglied << werden und >> Zugriff auf alle 26 Kurse << (inkl. >> Webinare << + Unterlagen) sichern ab 7,40 EUR/Monat
++ Besser geht’s nicht!! ++