Ma4 – Skalarprodukt: Berechnungen

In dieser Lerneinheit behandeln das Skalarprodukt. Wir zeigen dir, wie du das Skalarprodukt berechnest und den eingeschlossenen Winkel zwischen zwei Vektoren bestimmst.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: MA4 – Vektorrechnung

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Skalarprodukt – Grundlagen

Das Skalarprodukt ist das Ergebnis der Multiplikation zweier Vektoren $\vec{a}$ und $\vec{b}$ und ergibt eine Zahl, den sogenannten Skalar.

Was ist das Skalarprodukt?

Das Skalarprodukt, auch als inneres Produkt oder Punktprodukt bekannt, ist ein grundlegendes Konzept in der linearen Algebra und Vektorrechnung. Es ist ein Verfahren, das zwei Vektoren in einen einzelnen skalaren Wert umwandelt und viele Anwendungen in Mathematik, Physik und Ingenieurwesen findet.

Skalarprodukt: Koordinaten der Vektoren gegeben

Das Skalarprodukt wird wie folgt bestimmt:

Skalarprodukt

$\vec{a} \cdot \vec{b} = \left( \begin{array}{c} a_1 \\ a_2 \\ a_3 \end{array} \right) \cdot \left( \begin{array}{c} b_1 \\ b_2 \\ b_3 \end{array} \right) = a_1 \cdot b_1 + a_2 \cdot b_2 + a_3 \cdot b_3$

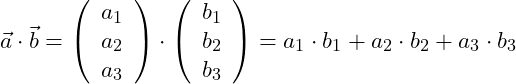
Die obige Formel kann dann angewendet werden, wenn die Koordinaten der Vektoren bekannt sind. Es können nur Vektoren der gleichen Größen miteinander multipliziert werden.

Schauen wir uns dazu mal ein Beispiel an:

Beispiel!

Gegeben seien die beiden Vektoren in der Ebene:

$\vec{a} = \left( \begin{array}{c} 1 \\ 5 \end{array} \right)$

$\vec{b} = \left( \begin{array}{c} 2 \\ -3 \end{array} \right)$

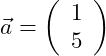
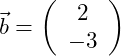
Bestimme $\vec{a} \cdot \vec{b}$ !

Da wir die Koordinaten der beiden Vektoren gegeben haben und die Vektoren dieselbe Größe aufweisen, können wir das Skalarprodukt gemäß der oben angegebenen Formel (angepasst auf die Ebene) bestimmen:

$\vec{a} \cdot \vec{b} = \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right) \cdot \left( \begin{array}{c} b_1 \\ b_2 \end{array} \right) = a_1 \cdot b_1 + a_2 \cdot b_2$

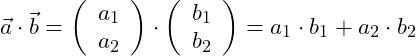
Wir setzen die gegebenen Werte in die Gleichung ein:

$\vec{a} \cdot \vec{b} = \left( \begin{array}{c} 1 \\ 5 \end{array} \right) \cdot \left( \begin{array}{c} 2 \\ -3 \end{array} \right) = 1 \cdot 2 + 5 \cdot (-3) = -13$

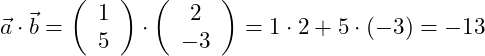
Das Skalarprodukt der beiden Vektoren ergibt -13. In der folgenden Grafik siehst du die beiden Vektoren eingezeichnet:

Skalarprodukt: Winkel berechnen

Sind die beiden Vektoren mit ihren Koordinaten gegeben und hast du das Skalarprodukt wie oben berechnet, so kannst du auch den Winkel φ zwischen den beiden Vektoren berechnen:

Für die Berechnung des Winkels, kannst du die folgende Formel verwenden:

Winkel berechnen

$\varphi = cos^{-1} (\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}})$

mit

$\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3$

$|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$

$|\vec{b}| = \sqrt{b_1^2 + b_2^2 + b_3^2}$

Schauen wir uns hierzu mal ein Beispiel an.

Beispiel!

Gegeben seien die beiden Vektoren in der Ebene:

$\vec{a} = \left( \begin{array}{c} 1 \\ 5 \end{array} \right)$

$\vec{b} = \left( \begin{array}{c} 2 \\ -3 \end{array} \right)$

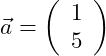
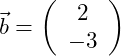
Bestimme den von den Vektoren eingeschlossenen Winkel $\varphi$ !

Wir haben hier zwei Vektoren mit ihren Koordinaten und derselben Größe gegeben, demnach können wir den eingeschlossenen Winkel der beiden Vektoren berechnen:

$\varphi = cos^{-1} (\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|})$

Zunächst bilden wir das Produkt:

$\vec{a} \cdot \vec{b} = a_1b_1 + a_2b_2 + a_3b_3 = 1 \cdot 2 + 5 \cdot (-3) = -13$

Danach berechnen wir die Länge der beiden Vektoren:

$|\vec{a}| = \sqrt{a_1^2 + a_2^2} = \sqrt{1^2 + 5^2} = \sqrt{26}$

$|\vec{b}| = \sqrt{b_1^2 + b_2^2} = \sqrt{2^2 + (-3)^2} = \sqrt{13}$

Wir können jetzt die berechneten Werte in die Gleichung einsetzen:

$\varphi = cos^{-1} (\frac{\vec{a} \cdot \vec{b}}{|\vec{a}||\vec{b}|}})$

$\varphi = cos^{-1} (\frac{-13}{\sqrt{26} \cdot \sqrt{13}})$

$\varphi = cos^{-1} (-0,707) = 135^{\circ}$

Der Winkel zwischen den beiden Vektoren beträgt 135°:

Skalarprodukt, Winkel berechnen, Länge von Vektoren, Vektorrechnung, eingeschlossener Winkel — Produkt, Winkel berechnen, Länge von Vektoren, Vektorrechnung, eingeschlossener Winkel

Skalarprodukt: Winkel gegeben

Es gibt eine weitere Möglichkeit das Skalarprodukt zu berechnen, wenn der eingeschlossene Winkel φ und die Längen der beiden Vektoren gegeben sind:

Skalarprodukt

$\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cos(\varphi)$

mit

$|\vec{a}| = \sqrt{a_1^2 + a_2^2 + a_3^2}$

$|\vec{b}| = \sqrt{b_1^2 + b_2^2 + b_3^2}$

Schauen wir uns hierzu ein Beispiel an.

Gegeben seien die Längen der beiden Vektoren in der Ebene sowie der eingeschlossene Winkel:

$|\vec{a}| = 2\sqrt{2}$

$|\vec{b}| = \sqrt{34}$

$\varphi = 104^{\circ}$

Bestimme das Produkt $\vec{a} \cdot \vec{b}$ !

Da wir die Längen sowie den eingeschlossenen Winkel gegeben haben, können wir das Skalarprodukt mittels der folgenden Formel berechnen:

$\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cos(\varphi)$

Einsetzen der gegebenen Werte:

$\vec{a} \cdot \vec{b} = 2\sqrt{2} \cdot \sqrt{34} \cos(104^{\circ}) = -4$

Das Produkt beträgt -4.

Anwendung des Skalarprodukts

Geometrie: Berechnung des Winkels zwischen zwei Vektoren.
Physik: Arbeit, die von einer Kraft entlang einer Strecke verrichtet wird.
Projektionsberechnung: Projektion eines Vektors auf einen anderen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist das Skalarprodukt?

Das Skalarprodukt ist eine Methode zur Multiplikation zweier Vektoren, die einen skalaren Wert ergibt.

2. Wie berechne ich das Skalarprodukt?

Multipliziere die entsprechenden Komponenten der Vektoren und summiere die Produkte.

3. Wofür wird das Skalarprodukt verwendet?

Es wird verwendet, um den Winkel zwischen Vektoren zu berechnen, Projektionen durchzuführen und physikalische Größen wie Arbeit zu bestimmen.

4. Wie hängt das Skalarprodukt mit dem Winkel zwischen Vektoren zusammen?

Dieses Produkt zweier Vektoren ist gleich dem Produkt ihrer Beträge und dem Kosinus des Winkels zwischen ihnen.

5. Was bedeutet ein Skalarprodukt von null?

Ein Produkt von null bedeutet, dass die Vektoren orthogonal (senkrecht) zueinander sind.

Zusammenfassung

Das Skalarprodukt ist ein wesentliches Werkzeug in der Vektorrechnung, das zwei Vektoren zu einem skalaren Wert kombiniert. Es findet breite Anwendung in der Geometrie, Physik und Ingenieurwesen.

Durch das Berechnen dieses Produkts können wir den Winkel zwischen Vektoren bestimmen, die orthogonale Projektion eines Vektors auf einen anderen durchführen und physikalische Größen wie die Arbeit berechnen.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++