In dieser Lerneinheit behandeln Geraden im dreidimensionalen Bereich und wollen dir zeigen, wie du die Parameterform einer Geraden im Raum aufstellen kannst und wie du die Gerade grafisch einzeichnest.
Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema. Mehr zu diesem Thema und der Mathematik findest du im Kurs: MA4 – Vektorrechnung Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik
Parameterform | Grundlagen
Auch für Geraden im Raum gibt es diese Form der Geradengleichung. Es gibt aber keine Koordinatenform oder Normalenform von diesen Geraden.
Was ist Parameterform für Geraden im Raum?
Die Parameterform für Geraden im Raum ist ein grundlegendes Konzept der analytischen Geometrie. Es ermöglicht die präzise Darstellung und Untersuchung von Geraden in einem dreidimensionalen Koordinatensystem.
Grundprinzipien
-
Definition der Parameterform:
- Eine Gerade im Raum kann durch einen Punkt
auf der Geraden und einen Richtungsvektor 
dargestellt werden. - Die Parameterform lautet:
, wobei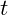 
ein reeller Parameter ist.
- Eine Gerade im Raum kann durch einen Punkt
-
Bestandteile dieser Form:
- Stützvektor : Ein fester Punkt auf der Geraden, dargestellt als Ortsvektor.
- Richtungsvektor : Ein Vektor, der die Richtung der Geraden angibt.
- Parameter 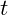: Ein variabler Wert, der jede Position auf der Geraden bestimmt.
- Stützvektor
-
Verwendung der Parameterform:
- Diese Form ist nützlich zur Beschreibung von Geraden in geometrischen Berechnungen, Schnittpunkten, Abständen und bei der Lösung von Gleichungssystemen.
Parameterdarstellung von Geraden (3D)
Für die Darstellung einer Geraden in Parameterform benötigen wir zwei Punkte auf der Geraden:
Um vom Punkt A nach Punkt B zu gelangen, müssen wir 3 Schritte in negative x-Richtung, 3 Schritte in positive y-Richtung und 5 Schritte in negative z-Richtung gehen (Berechnung: B – A):
Wir sind vom Punkt A zum Punkt mithilfe der 3 Koordinaten (x,y,z) gelangt. Dazu haben wir den Punkt A vom Punkt B subtrahiert:
Wir haben damit den Richtungsvektor 
bestimmt, der im Punkt A beginnt und auf den Punkt B zeigt. Der Punkt, indem der Richtungsvektor beginnt, wird auch als Aufpunkt 
bezeichnet.
Damit ergibt sich die folgende Form:
Zunächst geben wir den Punkt an, an welchem wir starten. Das ist nichts anderes als der Aufpunkt des Ortsvektors. Wir starten hier im Punkt A. Der Ortsvektor lautet also:
Von diesem Punkt aus gehen wir nun in Richtung des zweiten Punktes B. Dieser Abstand von Punkt A zu Punkt B ist der Richtungsvektor:
Der Parameter gibt dabei an, wie “weit” wir in diese Richtung gehen. Setzen wir 
, so gehen wir 3 Schritte in negative x-Richtung, 3 Schritte in positive y-Richtung und 5 Schritte in negative z-Richtung (landen also genau im Punkt B). Dabei darf alle Werte aus den reellen Zahlen annehmen, so dass jeder Punkt auf der Geraden beschrieben wird.
Allgemeine Gleichung der Parameterform
Dieses Form einer Geraden im Raum ist genau so aufgebaut, wie die Darstellung in der Ebene:
Hierbei ist der Aufpunkt des Ortsvektors (auch: Stützvektor) und der Richtungsvektor der Gerade g. ist der Parameter, der jede reelle Zahl annehmen kann.
Beispiel:
Wir betrachten hier Vektoren im Raum. Eine Zeichnung ist deswegen etwas schwieriger als in der Ebene, da wir ein dreidimensionales Koordinatensystem betrachten müssen:
Beispiel: Parameterform einer Geraden im Raum
Gegeben sei eine Gerade, die durch den Punkt P = (2|-4|1), in Richtung des Vektors 
verläuft.
Gibt die Geradengleichung an!
Es ist ganz einfach hier diese Form der Geraden zu wählen. Dazu benötigen wir einen Punkt auf der Geraden (hier gegeben mit P) und den Richtungsvektor. Dieser Vektor gibt die Richtung der Geraden an. Der Punkt auf der Geraden kann als Aufpunkt verwendet werden. Der Richtungsvektor ist bereits in der Aufgabenstellung gegeben.
Wir suchen diese Darstellung:
Mit dem Punkt und dem Vektor aus der Aufgabenstellung erhalten wir:
In der folgenden Grafik siehst du die Gerade eingezeichnet:
Wir tragen zunächst den Aufpunkt A ein. Danach gehen wir von diesem Punkt aus die x,y und z-Schritte des Richtungsvektors. Wir haben dann den Richtungsvektor gegeben, der im Aufpunkt beginnt und auf den Punkt P = (1|03) zeigt. Wir können jetzt die Gerade einzeichnen, indem wir eine Gerade durch diese beiden Punkte ziehen:
Anwendung der Parameterform
- Analytische Geometrie: Untersuchung von Geraden, Ebenen und Schnittpunkten.
- Physik: Beschreibung von Bewegung und Trajektorien.
- Ingenieurwesen: Konstruktion und Design von Strukturen und Mechanismen.
Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)
1. Was ist die Parameterform einer Geraden?
Diese Form einer Geraden beschreibt alle Punkte der Geraden durch einen festen Punkt (Stützvektor) und einen Richtungsvektor.
2. Wie finde ich den Richtungsvektor?
Der Richtungsvektor kann durch die Differenz zweier Punkte auf der Geraden oder direkt gegeben sein.
3. Was ist der Parameter t?
Der Parameter t ist ein reeller Wert, der die Position auf der Geraden variiert.
4. Kann diese Form für parallele Geraden verwendet werden?
Ja, parallele Geraden haben denselben Richtungsvektor, aber unterschiedliche Stützvektoren.
5. Wie bestimme ich den Schnittpunkt zweier Geraden?
Setze die Parameterformen gleich und löse das resultierende Gleichungssystem.
Zusammenfassung
Diese Form für eine Gerade im Raum bietet eine präzise Methode zur Darstellung und Analyse von Geraden in der analytischen Geometrie. Durch die Kombination eines stützenden Vektors und eines Richtungsvektors kann jede Gerade im Raum beschrieben werden.
Diese Darstellung ist in vielen wissenschaftlichen und technischen Bereichen von großer Bedeutung und ermöglicht die Untersuchung von Schnittpunkten, Abständen und geometrischen Beziehungen.
In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.
Was gibt es noch bei uns?
Optimaler Lernerfolg durch tausende Übungsaufgaben
Quizfrage 1
Quizfrage 2
“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”
Was ist Technikermathe?
Unser Dozent Jan erklärt es dir in nur 2 Minuten!
Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!
Geballtes Wissen in derzeit 26 Kursen
Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen
WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.
Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs
++ Günstiger geht’s nicht!! ++
Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++
Social Media? - Sind wir dabei!
Dein Technikermathe.de-Team
