MA4 – Koordinatenform einer Ebene

In dieser Lerneinheit behandeln wir die Koordinatenform von Ebenen und wollen dir zeigen, wie du einen Punkt auf der Ebene und den Normalenvektor mittels Koordinatenform bestimmst.

Für ein optimales Verständnis helfen dir drei ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Mehr zu diesem Thema und der Mathematik findest du im Kurs: MA4 – Vektorrechnung

Oder lieber mit den Grundlagen starten? Alles dazu findest du im Kurs: Ma1-Grundlagen der Mathematik

Koordinatenform einer Ebene | Grundlagen

Ebenen im Raum können unterschiedlich dargestellt werden. Eine Möglichkeit der Darstellung ist über die Koordinatenform. Aus der Koordinatenform einer Ebene kannst du den Normalenvektor, der senkrecht auf der Ebene steht, sofort ablesen. Außerdem ist die Bestimmung der Spurpunkte der Ebene (Schnittpunkte mit den Koordinatenachsen) sehr einfach.

Koordinatenform einer Ebene? Detaillierte Erklärung und Berechnung

Die Koordinatenform einer Ebene ist ein fundamentales Konzept in der analytischen Geometrie. Diese Form ermöglicht die präzise Beschreibung und Analyse von Ebenen im dreidimensionalen Raum, was in Bereichen wie Ingenieurwesen, Physik und Computergraphik von großer Bedeutung ist.

Grundprinzipien

Definition der Koordinatenform:
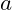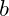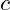- Die Koordinatenform einer Ebene ist eine Gleichung der Form: $ax + by + cz = d$ . Hierbei sind $a$ , $b$ und $c$ die Koeffizienten des Normalenvektors der Ebene, und 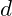$d$ ist ein Skalar.
Normale und Ebene:
- Der Vektor $\vec{n} = (a, b, c)$ ist der Normalenvektor der Ebene, der senkrecht auf der Ebene steht.
- Jeder Punkt $(x, y, z)$ auf der Ebene erfüllt die Koordinatengleichung.
Herleitung der Koordinatenform:
- Die Koordinatenform kann aus der Punkt-Normalen-Form der Ebene hergeleitet werden: $\vec{n} \cdot (\vec{r} - \vec{r_o}) = 0$ , wobei $\vec{r_0}$ ein Punkt auf der Ebene ist.

Koordinatenform einer Ebene | Formeln

Wir haben bereits die Koordinatenform einer Geraden in der Ebene kennengelernt:

$ax+by=c$

mit

$a,b,c \in \mathbb{R}$

Jeder Punkt (x,y) der diese Gleichung erfüllt, liegt auf der Geraden.

Wir betrachten hier die Koordinatenform einer Ebene, die wie folgt aussieht:

Koordinatenform der Ebene

$ax+by + cz = d$

mit

$a,b,c,d \in \mathbb{R}$

Jeder Punkt (x,y,z) der diese Gleichung erfüllt, liegt auf der Ebene.

Beispiel 1 | Punkt auf Ebene ermitteln

Beispiel!

Gegeben sei die Ebene in Koordinatenform:

$E: 4x + 2y + 3z = 12$

Liegt der Punkt (1|-2|4) auf der Ebene?

Um herauszufinden, ob ein Punkt auf einer Ebene liegt, setzen wir diesen Punkt in die Koordinatenform ein und schauen, ob die Gleichung erfüllt wird:

$4 \cdot 1 + 2 \cdot (-2) + 3 \cdot 4 = 12$

$12 = 12$

Da die linke Seite und die rechte Seite gleich sind, ist die Gleichung erfüllt. Damit liegt der Punkt auf der Ebenen.

Schauen wir uns in der folgenden Grafik zunächst die Ebene E an:

Koordinatenform einer Ebene, Ebenen im Raum, Ebene zeichnen

Wir haben die Ebene E begrenzt eingezeichnet. Die Zeichnung der Ebene haben wir so vorgenommen, dass wir zunächst die Spurpunkte (Schnittpunkte der Ebene mit den Koordinatenachsen) berechnet haben und daraus die Parameterform aufgestellt haben. Die Einzeichnung der Parameterform ist mit Aufpunkt und Richtungsvektoren sehr einfach vorzunehmen (siehe vorherige Lektion Ebenen: Parameterform).

Info:

Die Berechnung der Spurpunkte folgt in der nachfolgenden Lektion Spurpunkte einer Ebene und die Umwandlung von der Koordinatenform in Parameterform in der folgenden Lektion Umwandlung der Ebenengleichungen.

In der nachfolgenden Grafik siehst du erneut die Ebene E mit ihren Spurpunkten sowie dem Punkt P. Dazu haben wir die Ebene vergrößert, so dass auch zu erkennen ist, dass der Punkt auf der Ebene liegt:

Punkt auf Ebene, Ebenen, Ebenen im Raum, Koordinatenform, Parameterform, Spurpunkte

In der obigen Grafik siehst du den Punkt P(1|-2|4) eingezeichnet, der auf der Ebene E liegt.

Normalenvektor – Koordinatenform

Aus den Koeffizienten a, b und c können wir den Normalenvektor bestimmen. Das ist der Vektor, der senkrecht (im 90°-Winkel) auf der Ebene steht. Man sagt auch, der Normalenvektor ist orthogonal zur Ebene.

Der Normalenvektor wird aus den Koeffizienten der Koordinatenform wie folgt bestimmt:

$E: \textbf{a}x + \textbf{b}y + \textbf{c}z = d$

$\vec{n} = \left( \begin{array}{c} a \\ b \\ c \end{array}\right)$

Beispiel 2 | Normalenvektor bestimmen

Beispiel!

Gegeben sei die Ebene in Koordinatenform:

$E: 4x + 2y + 3z = 12$

a) Wie lautet der dazugehörige Normalenvektor?

b) Gibt es nur einen Normalenvektor zu einer Ebene?

Lösung a)

Zunächst bestimmen wir den Normalenvektor der gegebenen Ebene aus den Koeffizienten a, b und c:

$\vec{n} = \left( \begin{array}{c} a \\ b \\ c \end{array}\right)$

$\vec{n} = \left( \begin{array}{c} 4 \\ 2 \\ 3 \end{array}\right)$

Wir wollen uns jetzt den berechneten Normalenvektor $\vec{n}$ anschauen, der senkrecht auf dieser Ebene E steht:

In der obigen Grafik ist der Normalenvektor der Ebene E eingezeichnet. Wir sehen genau, dass der Normalenvektor $\vec{n}$ vom Ursprung auf die Ebene zeigt bzw. bei Verlängerung durch sie durchgeht und dann im 90°-Winkel auf dieser steht.

Lösung b)

Da der Normalenvektor senkrecht zu einer Ebene liegt, ist alleine die Richtung von Bedeutung. Je nachdem auf welcher Seite der Ebene man den Normalenvektor platziert, zeigt er in zwei verschiedene Richtungen. Die Länge des Normalenvektors ist nicht entscheidend, kann also beliebig variiert werden. Daher gibt es nicht den einen Normalenvektor, sondern unendlich viele. Alle Vielfache des berechneten Normalenvektors, sind demnach ebenfalls Normalenvektoren der Ebene.

Sonderfälle der Koordinatenform

Es gibt einige Sonderfälle der Koordinatenform, die anhand der Koeffizienten a,b,c und d zu erkennen sind:

a = 0: Die Ebene verläuft parallel zur x-Achse:

Ebene parallel zur x-Achse, Ebene, Ebenen im Raum

In der obigen Grafik siehst du die blaue Ebene einzeichnet, die parallel zur x-Achse verläuft. Da a = 0 ist, fällt in der Koordinatendarstellung die x-Koordinate weg, damit sind nur noch die y- und z-Koordinaten enthalten. Damit existiert der Schnittpunkt der Ebene mit der x-Achse nicht und damit ist die Ebene parallel zur x-Achse.

b = 0: Die Ebene verläuft parallel zur y-Achse:

Ebene parallel zur y-Achse, Ebene parallel, Ebenen im Raum

In der obigen Grafik siehst du die blaue Ebene einzeichnet, die parallel zur y-Achse verläuft. Da b = 0 ist, fällt in der Koordinatendarstellung die y-Koordinate weg, damit sind nur noch die x- und z-Koordinaten enthalten. Damit existiert der Schnittpunkt der Ebene mit der y-Achse nicht und damit ist die Ebene parallel zur y-Achse.

c = 0: Die Ebene verläuft parallel zur z-Achse

Ebene parallel zur z-Achse, Ebenen im Raum

In der obigen Grafik siehst du die blaue Ebene einzeichnet, die parallel zur z-Achse verläuft. Da c = 0 ist, fällt in der Koordinatendarstellung die z-Koordinate weg, damit sind nur noch die x- und y-Koordinaten enthalten. Damit existiert der Schnittpunkt der Ebene mit der z-Achse nicht und damit ist die Ebene parallel zur z-Achse.

d = 0: Die Ebene verläuft durch den Koordinatenursprung

Ebene durch Ursprung, Ebenen im Raum, d = 0

d = 1: Die Ebene schneidet die Achsen bei (1/a|0|0), (0|1/b|0) und (0|0|1/c):

Ebenen im Raum, d = 1, Ebene einzeichnen

In der obigen Grafik haben wir die Ebene $E: x + y + z = 1$ gegeben. Wir haben d = 1 gegeben, damit können wir die Schnittpunkte der Ebene mit den Koordinatenachsen direkt aus den Koeffizienten der Ebenengleichung bestimmen. Mit a = 1, b = 1 und c = 1 ergeben sich die folgenden Schnittpunkte:

$P_1(1|0|0)$ , $P_2(0|1|0)$ und $P_3(0|0|1)$

Anwendung der Spurpunkte

Ingenieurwesen: Analyse von Flächen und Strukturen in der Konstruktion.
Physik: Untersuchung von Ebenen in Raum und Zeit.
Computergraphik: Rendering und Modellierung von Oberflächen.

Mögliche Fragestellungen | Häufig gestellte Fragen (FAQs)

1. Was ist die Koordinatenform einer Ebene?

Die Koordinatenform ist eine Gleichung der Form $ax + by + cz = d$ , die eine Ebene im dreidimensionalen Raum beschreibt.

2. Wie wird die Koordinatenform hergeleitet?

Die Koordinatenform kann aus der Punkt-Normalen-Form der Ebene abgeleitet werden, indem man den Normalenvektor und einen Punkt auf der Ebene verwendet.

3. Wann verwendet man die Koordinatenform?

Die Koordinatenform wird verwendet, um Ebenen in der analytischen Geometrie zu beschreiben und zu analysieren.

4. Was ist ein Normalenvektor?

Ein Normalenvektor ist ein Vektor, der senkrecht auf der Ebene steht und ihre Richtung bestimmt.

5. Kann eine Ebene durch drei Punkte definiert werden?

Ja, solange die drei Punkte nicht kollinear sind, können sie eindeutig eine Ebene definieren.

Zusammenfassung

Die Koordinatenform einer Ebene $ax + by + cz = d$ ist eine zentrale Methode zur Beschreibung von Ebenen im dreidimensionalen Raum. Sie kann aus einem Punkt auf der Ebene und einem Normalenvektor hergeleitet werden. Diese Form ist in vielen praktischen Anwendungen unverzichtbar, von der Analyse von Strukturen im Ingenieurwesen bis hin zur Modellierung von Oberflächen in der Computergraphik.

Was kommt als Nächstes?

In der folgenden Lerneinheit zeigen wir dir, wie Ableiten mit der Produktregel abläuft.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen — Übungsbereich (Demo) – Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++