MA3 – Nullstellen bei ln-Funktionen

In dieser Lerneinheit unseres Onlinekurses Ma3-Kurvendiskussion, wollen wir uns anschauen, wie die Nullstellen bei ln-Funktionen bestimmt werden.

Die Nullstellen von Funktionen sind die Schnittpunkte der Funktion mit der x-Achse. Der y-Wert ist an dieser Stelle Null.

Nullstellen bei ln-Funktionen

Eine Nullstelle ist dann gegeben, wenn die Funktion die x-Achse schneidet. Damit ist der y-Wert (=Funktionswert) an dieser Stelle gleich Null: f(x) = 0.

Die Bedingung für eine Nullstelle ist also, dass der Funktionswert zu Null wird. Zur Bestimmung der Nullstellen von Funktionen müssen wir also die gegebene Funktion gleich Null setzen und dann nach x auflösen. Wir ermitteln so die Stelle für x, bei welchem die Funktion zu Null wird. Damit liegt für diese Stelle eine Nullstelle vor.

Merk’s dir!

Jede “reine” Logarithmusfunktion hat eine Nullstelle bei x = 1.

In der nachfolgenden Grafik siehst du zwei ln-Funktionen f(x) = ln(x) und f(x) = ln(x²). Beide haben eine Nullstelle bei x = 1. Die Logarithmusfunktion mit den geraden Exponenten weist zusätzlich eine Nullstelle bei x = -1 auf. Das ist möglich, weil bei geraden Exponenten auch negative x-Werte im Definitionsbereich liegen. Das Minuszeichen fällt bei geraden Exponenten weg: f(-2) = ln((-2)²) = ln(2²) = ln(4).

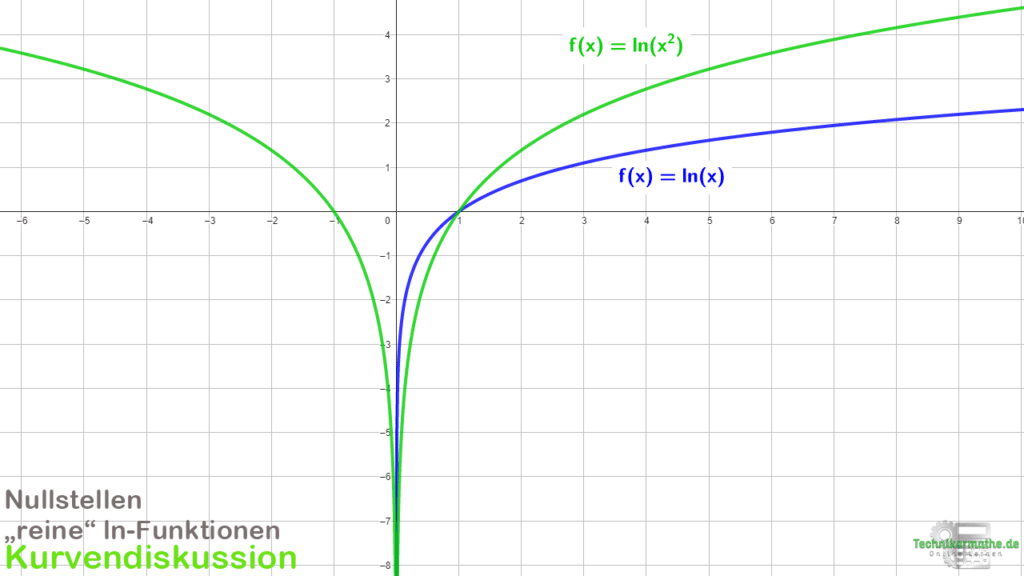
Nullstellen, ln-Funktion, Logarithmusfunktion

Weitere Nullstellen einer ln-Funktion

Es gibt natürlich auch verschachtelte Logarithmusfunktionen. Diese beinhalten dann noch andere Funktionen, wie z.B. f(x) = ln(x) · (x² – 9). Hier gibt es dann insgesamt zwei Nullstelle. Eine Nullstelle bei x₁ = 1 aus der Logarithmusfunktion und eine Nullstellen aus der quadratischen Funktion bei x₂ = 3. Aus der quadratischen Funktion (x² – 9) würden wir eigentlich zwei Nullstellen bei x = 3 und x = -3 ermitteln. Durch die Logarithmusfunktion ist die negative Nullstelle aber nicht gegeben, da der Definitionsbereich keine negativen x-Werte zulässt:

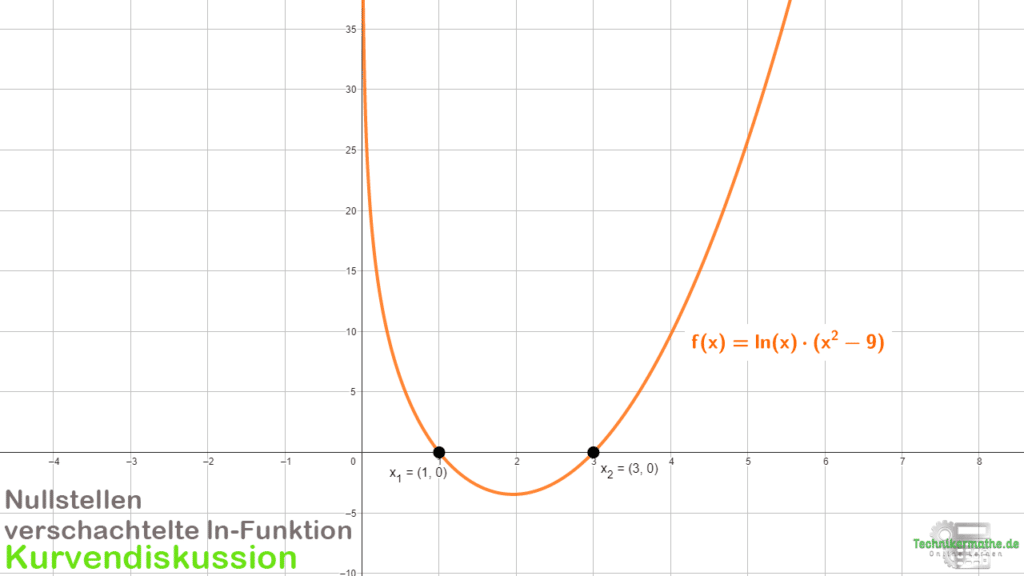
Satz vom Nullprodukt

Der “Satz vom Nullprodukt” besagt, dass die Faktoren eines Produktes einzeln auf Nullstellen untersucht werden können.

Betrachten wir dazu das folgende Beispiel:

Beispiel!

$f(x) = ln(x) \cdot (x^2 - 36)$

Wir haben hier ein Produkt gegeben, welches aus zwei Faktoren (ln-Funktion und Klammer) besteht. Die beiden Faktoren können hier separat auf Nullstellen untersucht werden. Wird ein Faktor zu Null, so wird der gesamte Ausdruck zu Null. Wir können also beide Faktoren gleich Null setzen und die Nullstellen bestimmen.

$x^2 - 36 = 0$

$x = \pm\sqrt{36}$

$x_1 = 6$

$x_2 = -6$

$ln(x) = 0$ |e-Funktion auf beiden Seiten anwenden

$e^{ln(x)} = e^0$

e-Funktion und ln-Funktion heben sich auf. Damit verbleibt auf der linken Seite x:

$x = e^0$ |e⁰ = 1

$x = 1$

Damit erhalten wir aus der ln-Funktion die Nullstelle x₃ = 1.

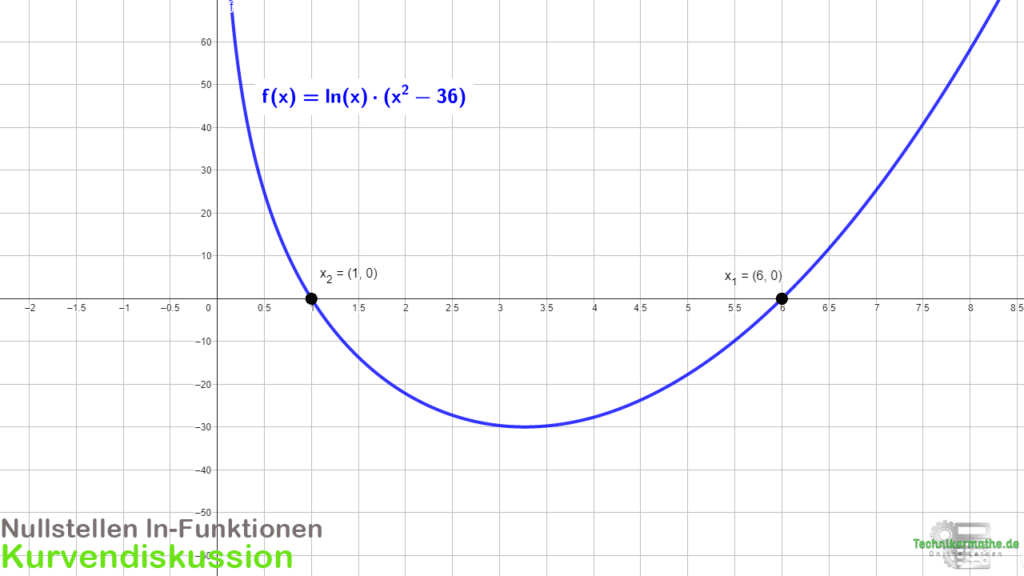
Wir haben hier nun drei mögliche Nullstellen gegeben. Da wir aber ln(x) gegeben haben und negative Werte für x nicht definiert sind, liegt bei x = -6 keine Nullstelle vor. Dazu können wir auch einfach die Probe machen und x = -6 einsetzen:

$f(x = -6) = ln(-6) \cdot ((-6)^2 - 36) =$ nicht definiert

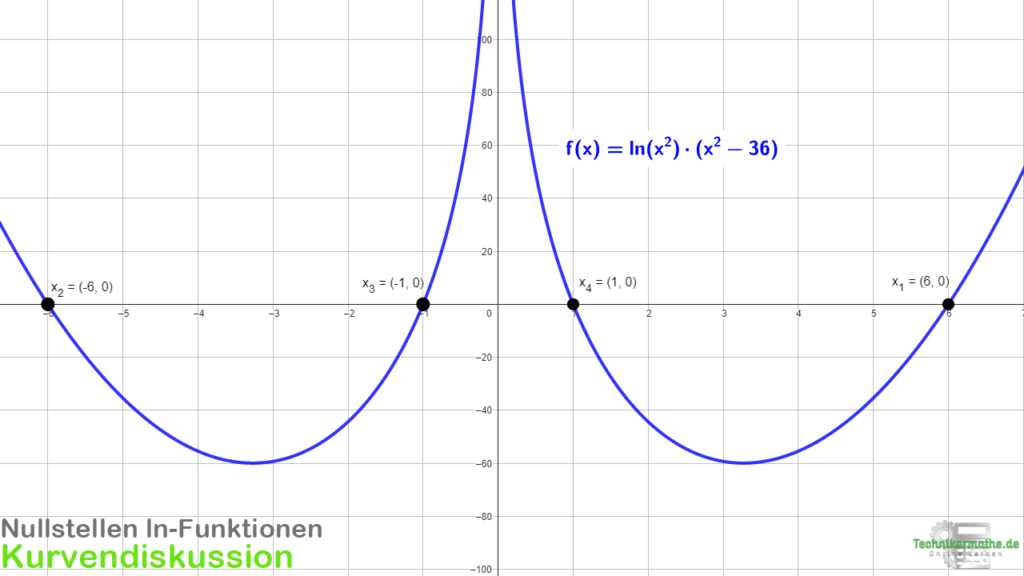
Betrachten wir hier ein Beispiel mit ln-Funktion und geradem Exponenten:

Beispiel!

$f(x) = ln(x^2) \cdot (x^2 - 36)$

$x^2 - 36 = 0$

$x = \pm\sqrt{36}$

$x_1 = 6$

$x_2 = -6$

$ln(x^2) = 0$ |e-Funktion auf beiden Seiten anwenden

$e^{ln(x^2)} = e^0$

e-Funktion und ln-Funktion heben sich auf:

$x^2 = e^0$ |e⁰ = 1

$x^2 = 1$

$x = \pm\sqrt{1}$

$x_3 = 1$

$x_4 =-1$

Wir haben hier vier Nullstellen gegeben. Auch die negativen Nullstellen treten hier auf, weil für ln(x²) alle reellen Zahlen für x eingesetzt werden können, auch negative Zahlen:

$f(x = -6) = ln((-6)^2) \cdot ((-6)^2 - 36) = 0$

Damit liegen hier die Nullstellen x₁=6, x₂ = -6, x₃ = 1, x₄ = -1 vor.

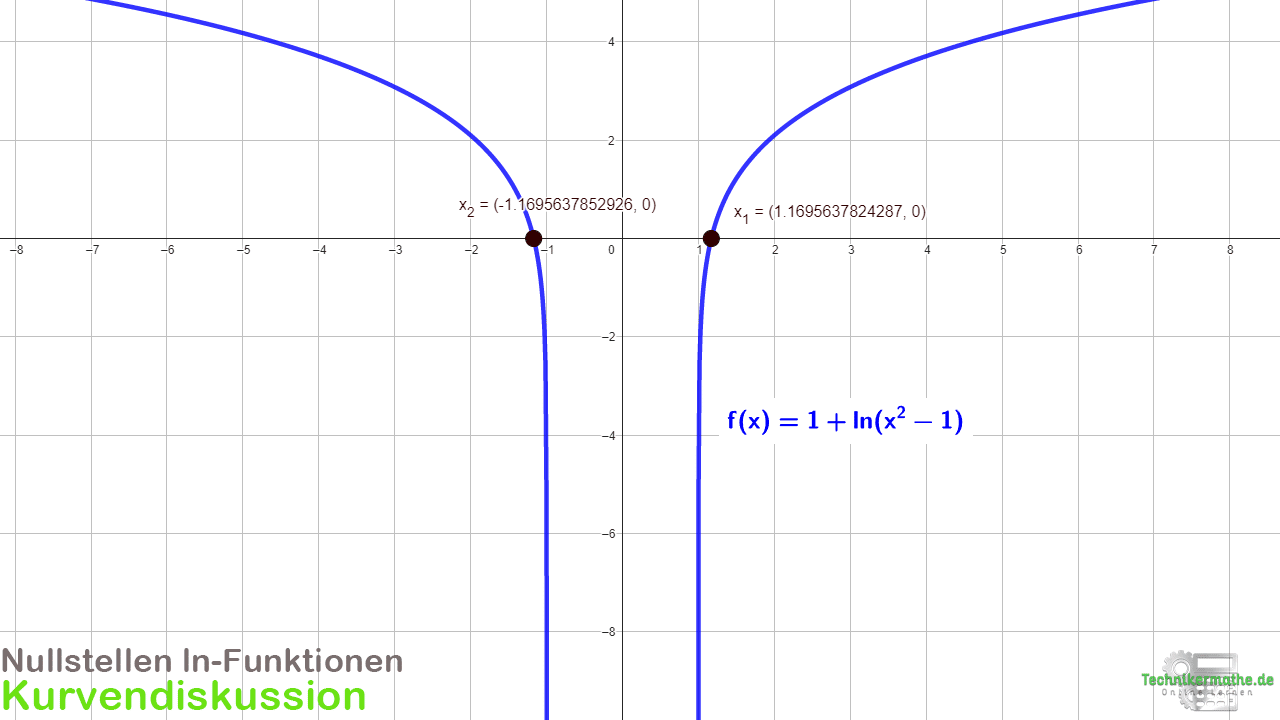
Beispiel 1: Definitionsbereich und Nullstellen

Gegeben sei die folgende Funktion:

$f(x) = 1 + ln(x^2 -1)$

Gib den Definitionsbereich an und bestimme die Nullstellen!

Definitionsbereich

Zunächst bestimmen wir den Definitionsbereich bzw. die Definitionslücken, um diejenigen x-Werte zu bestimmen, die nicht innerhalb des Definitionsbereichs liegen. Eine Definitionslücke bei einer ln-Funktion ist dann gegeben, wenn das Argument den Wert Null annimmt oder negativ wird. Deswegen schauen wir uns mal die Logarithmusfunktion an:

$ln(x^2-1)$

Der Wert in der Klammer (=Argument) wird null, wenn wir für x = 1 oder x = -1 einsetzen. Damit ist der Definitionsbereich alle reellen Zahlen außer x = 1 und x = -1, denn dann wird das Argument zu Null:

$ln(1^2 - 1) = ln(0)$ nicht definiert

$ln((-1)^2 -1) = ln(0)$ nicht definiert

Für diese Funktion ist die Null auch nicht im Definitionsbereich enthalten, weil der Wert in der Klammer dann negativ wird:

$ln(0^2 - 1) = ln(-1)$ nicht definiert

Alle anderen reellen Zahlen, auch die negativen, sind im Definitionsbereich enthalten. Denn das x² sorgt dafür, dass auch eine negative Zahl positiv wird. Damit ergibt sich der folgende Definitionsbereich:

$D = \mathbb{R} \setminus \{-1,0,1\}$ Definitionsbereich

Nullstellen

Als nächstes bestimmen wir die Nullstellen, indem wir die Funktion gleich Null setzen:

$f(x) = 0$

$1 + ln(x^2 -1) = 0$ |-1

$ln(x^2 - 1) = -1$ |e-Funktion

$x^2 - 1 = e^{-1}$ |+1

$x^2 = e^{-1} + 1$ |√

$x_{1,2} = \pm \sqrt{e^{-1} + 1}$

$x_1 = 1,1696$

$x_2 = -1,1696$

Wir haben hier die beiden Nullstellen der Funktion gegeben. Zur Probe können wir diese in die Funktion einsetzen. Der Funktionswert muss Null ergeben:

$f(1,17) = 1 + ln(1,1696^2 -1) \approx 0$

$f(-1,17) = 1 + ln((-1,1696)^2 -1) \approx 0$

Wir haben hier die Nullstellen der Funktion bestimmt wie wir in der folgenden Grafik sehen. Es resultiert nicht genau Null, weil wir die x-Werte gerundet haben und damit Rundungsfehler auftreten. Die Nullstelle ist nicht bei x = 1 gegeben, da wir hier keine “reine” ln-Funktion gegeben haben.

Nullstellen bei ln-Funktionen, Definitionsbereich, ln-Funktion, Logarithmusfunktion

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

Quizfrage 2

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus jedem unserer Kurse!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Zugriff auf alle 26 Kurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++