TM1 – Ritterschnittverfahren einfach anwenden

Was ist das Ritterschnittverfahren?

Definition

Was ist das Ritterschnittverfahren?

Das Ritterschnittverfahren ist eine ingenieurtechnische Methode zur Bestimmung von inneren Kräften in Fachwerken. Durch das gezielte Schneiden des Fachwerks an drei nicht-konkurrierenden Stäben lassen sich die unbekannten Kräfte mittels statischer Gleichgewichtsbedingungen (Kraft- und Momentengleichungen) schnell und effizient berechnen. Es wird häufig eingesetzt, um die Stabilität und Belastbarkeit von Tragwerken zu analysieren.

Das Ritterschnittverfahren dient der Berechnung festgelegter Stabkräfte in einem Fachwerk anhand der drei Gleichgewichtsbedingungen der Ebene. Dazu wird ein Schnitt durch das Fachwerk durchgeführt, so dass dieses in zwei Teilen vorliegt.

Wir betrachten hier die Berechnung der unbekannten Stabkräfte mittels Ritterschnittverfahren.

Für ein optimales Verständnis helfen dir vier ausführliche Videoclips und ein anschauliches Rechenbeispiel zu dem Thema.

Mehr zu diesem Thema und der Statik findest du im Kurs: Onlinekurs TM1-Statik.

In dieser Lerneinheit schauen wir uns das Ritterschnittverfahren (auch: Ritter’sche Schnittverfahren) zur Berechnung der unbekannten Stabkräfte in einem Fachwerk an. Dabei lösen wir nachfolgende Fragestellungen:

Wie prüft man das Fachwerk auf statische Bestimmtheit mittels Abzählformel?
Wie berechnet man die Auflagerkräfte?
Wie bestimmt man die Winkel von den Stabkräften zur Waagerechten mittels Trigonometrie?
Wie ermittelt man die Stabkräfte aus den Gleichgewichtsbedingungen mittels Ritterschnittverfahren?

Ritterschnittverfahren: Beschreibung

Für die Berechnung der unbekannten Stabkräfte in einem Fachwerk, kannst du das Ritterschnittverfahren anwenden. Dazu wird das Fachwerk in zwei Teile zerlegt, indem durch die Stäbe des Fachwerks geschnitten wird. Grundsätzlich kannst du durch beliebig viele Stäbe schneiden. Damit du aber am Ende aus den drei Gleichgewichtsbedingungen der Ebene die unbekannten Stabkräfte berechnen kannst (3 Stabkräfte aus 3 Gleichgewichtsbedingungen), solltest du den Schnitt wie folgt durchführen:

Ritterschnittverfahren, Regeln, Ritterschnittverfahren, Fachwerk, Schnitt durch das Fachwerk, Beispiel — Ritterschnittverfahren: Schnitt durch das Fachwerk

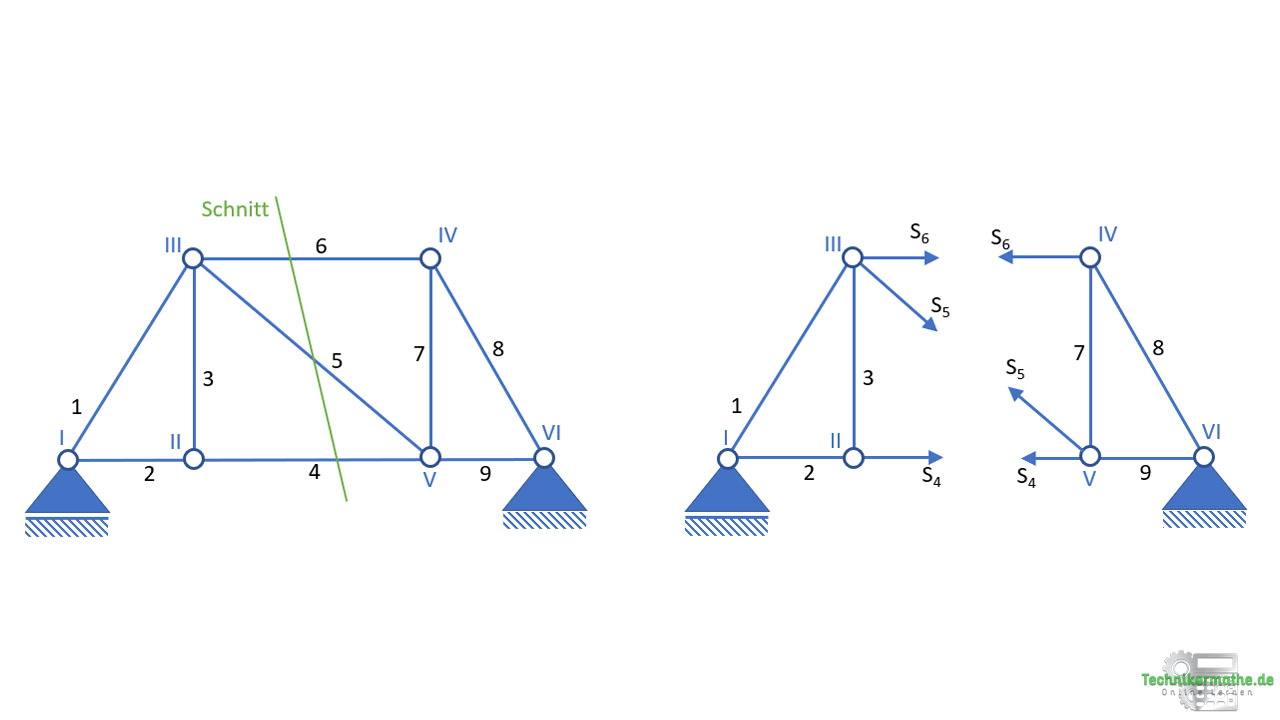
Der Schnitt kann durch drei Stäbe des Fachwerks erfolgen, die nicht alle in einem Knoten liegen. Das Fachwerk muss nach dem Schnitt in zwei Teilen vorliegen. In der obigen Grafik haben wir den Schnitt durch die drei Stäbe S₆, S₅ und S₄ durchgeführt. Damit liegen die drei Stäbe frei und können mittels der drei Gleichgewichtsbedingungen in der Ebene berechnet werden.

Gleichgewichtsbedingungen:

$\sum S_{ix} = 0$

Summe aller Kräfte in x-Richtung

$\sum S_{iy} = 0$

Summe aller Kräfte in y-Richtung

$\sum M_i^{(X)} = 0$

Summe aller Momente

Unterschied zwischen Ritterschnittverfahren und Knotenpunktverfahren

Der Unterschied liegt darin, dass beim Knotenpunktverfahren jeder Knoten freigeschnitten wird und beim Ritterschnittverfahren das Fachwerk in zwei Teile zerlegt wird. Beim Knotenpunktverfahren werden dann mittels der Gleichgewichtsbedingungen in x- und y-Richtung maximal zwei unbekannte Stabkräfte pro Knoten bestimmt. Beim Ritterschnittverfahren hingegen können dann alle drei Gleichgewichtsbedingungen der Ebene auf die beiden Fachwerksteile angewendet werden, um die drei freigeschnittenen Stäbe zu bestimmen.

Das Ritterschnittverfahren ist gerade dann von Vorteil, wenn du nur einige wenige Stäbe aus dem Fachwerk berechnen sollst.

Videoreihe: Ritterschnittverfahren

In der folgenden Videoreihe schauen wir uns an, wie mittels Ritterschnittverfahren die unbekannten Stabkräfte in einem Fachwerk berechnet werden können.

Ritterschnittverfahren

Beispiel: Ritterschnittverfahren

Schauen wir uns an einem Beispiel an, wie das Ritterschnittverfahren funktioniert.

Ritterschnittverfahren, Beispiel, Berechnung, Fachwerk, Stäbe, Knoten, Lagerkräfte — Beispiel: Anwendung des Ritterschnittverfahrens

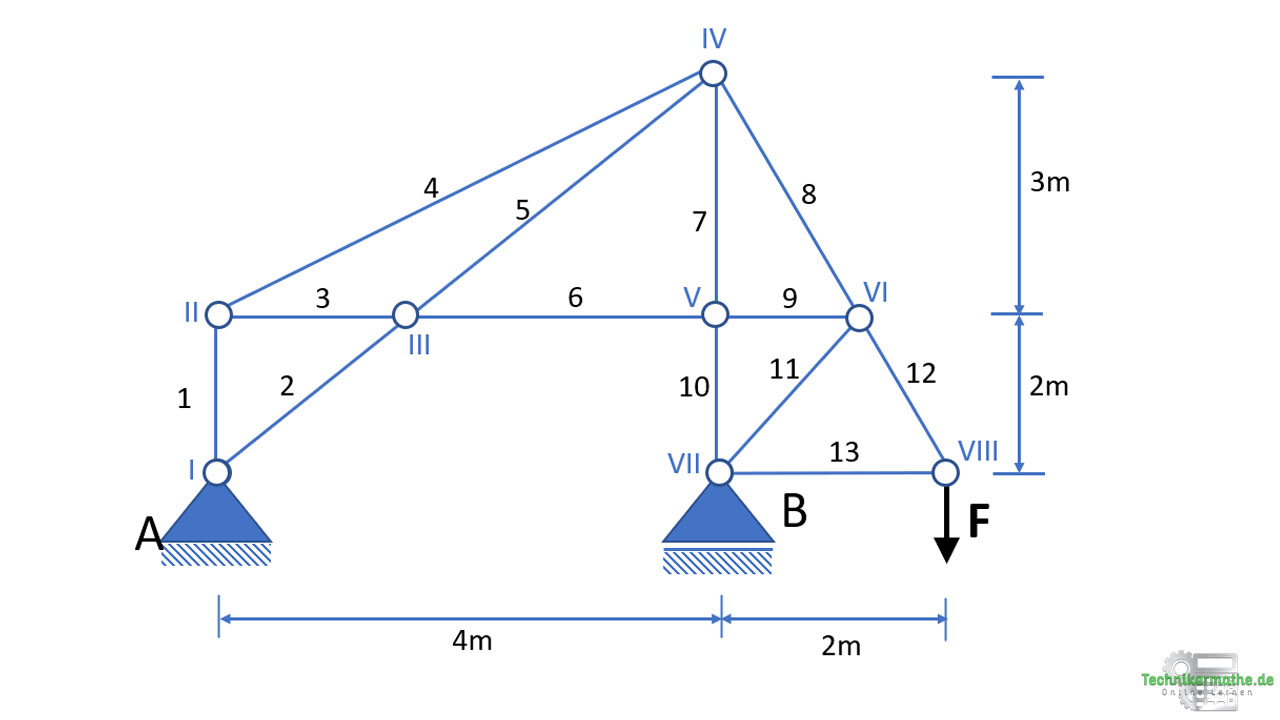
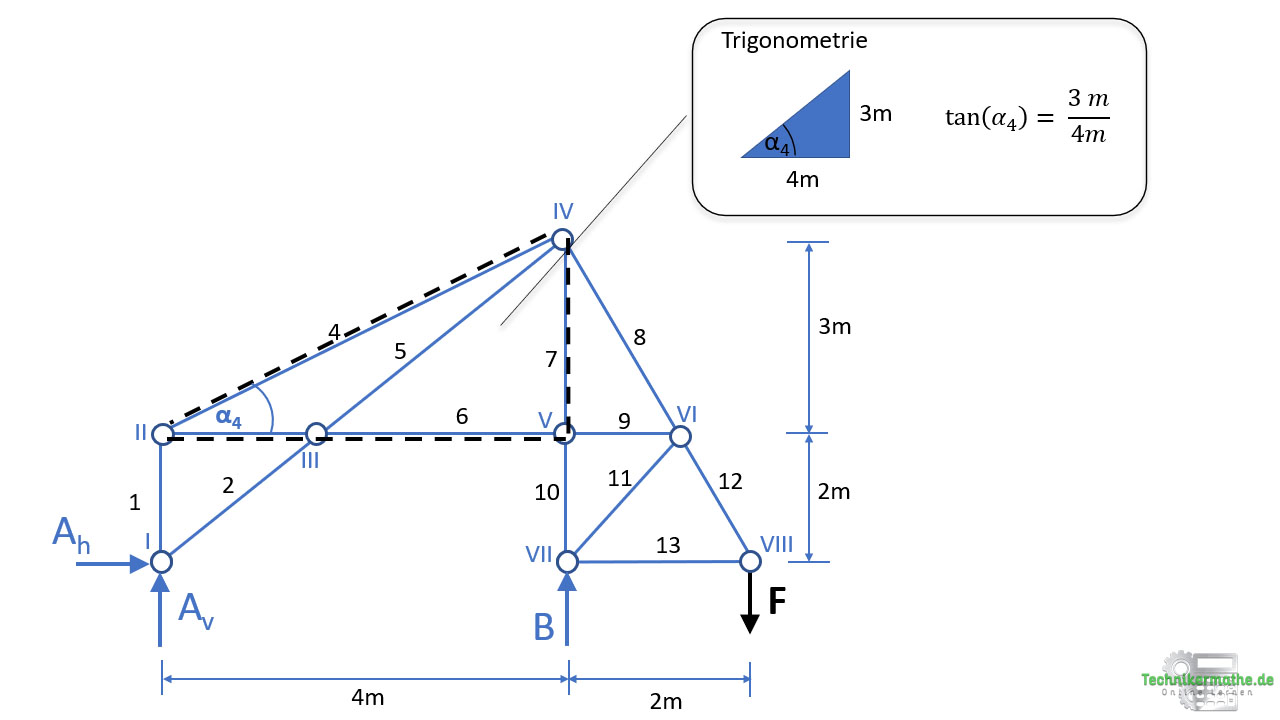
Gegeben sei das obige Fachwerk, welches auf einem Festlager A und einem Loslager B gelagert ist. An das Fachwerk greift eine äußere Kraft F = 50 kN an.

a) Prüfe das Fachwerk auf statische Bestimmtheit mittels Abzählformel!

b) Bestimme die Auflagerkräfte.

c) Bestimme die Stabkräfte S₄, S₅ und S₆ mittels Ritterschnittverfahren.

Statische Bestimmtheit

Wir starten mit dem Aufgabenteil a) und prüfen das obige Fachwerk mittels Abzählformel auf statische Bestimmtheit:

$f = a + s - 2k$ Abzählformel für Fachwerke

Das Fachwerk hat a = 3 Auflagerkräfte, s = 13 Stäbe und k = 8 Knoten.

$f = a + s - 2k = 3 + 13 - 2 \cdot 8 = 0$

Da f = 0 ist das obige Fachwerk statisch bestimmt.

Fachwerk freischneiden und Auflagerkräfte berechnen

Im nächsten Schritt müssen wir das Fachwerk von den Auflagern freischneiden und die unbekannten Auflagerkräfte abtragen:

Ritterschnittverfahren, Auflagerkräfte, Lagerkräfte, Fachwerk, Beispiel, Knoten — Freischnitt der Auflagerkräfte

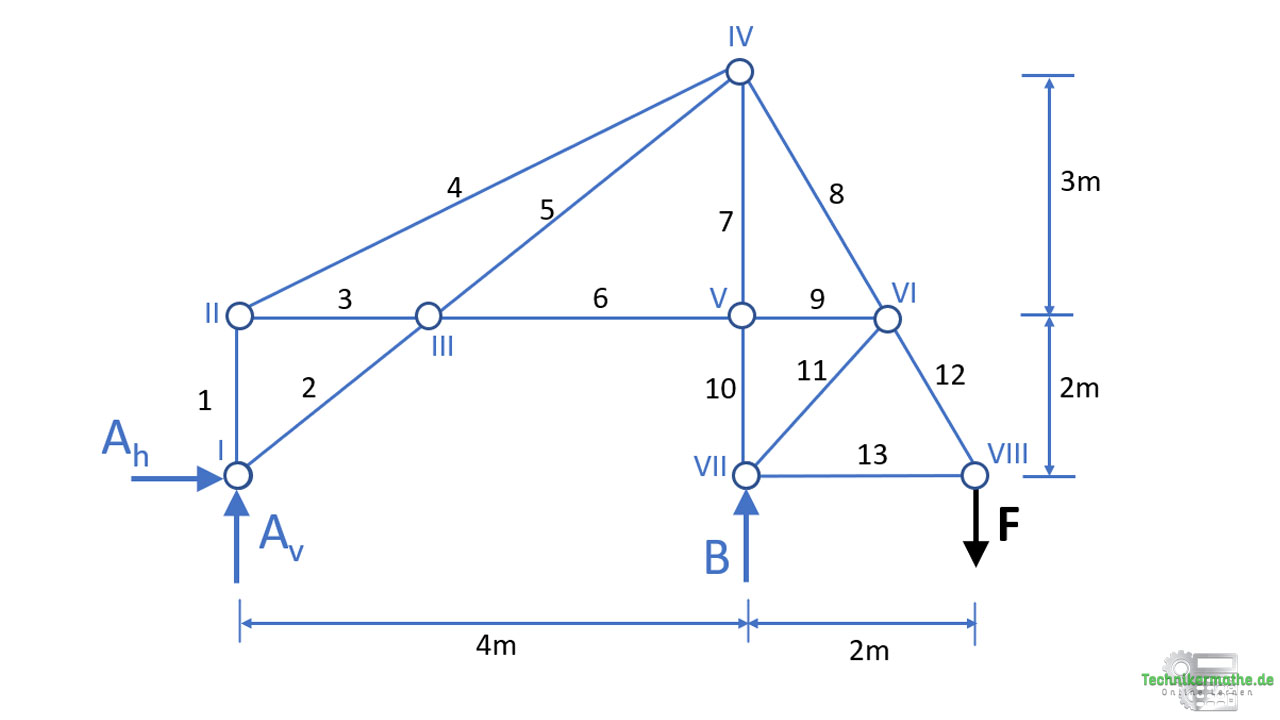
Die Auflagerkräfte können wir mit den drei Gleichgewichtsbedingungen der Ebene berechnen:

$\sum F_{ix} = 0$

$\sum F_{iy} = 0$

$\sum M_i = 0$

Wir starten mit der Gleichgewichtsbedingung in x-Richtung. Da keine äußeren horizontalen Kräfte an das Fachwerk angreifen, ist die horizontale Auflagerkraft A_h gleich Null:

$\sum F_{ix} = 0: \; A_h = 0$

Als nächstes wenden wir die Gleichgewichtsbedingung in y-Richtung an, indem wir alle vertikalen Kräfte summieren. Kräfte die nach oben zeigen berücksichtigen wir positiv, Kräfte die nach unten zeigen negativ:

$\sum F_{iy} = 0: \; \; A_v + B - F = 0$

Wir haben hier zwei unbekannte Kräfte A_v und B gegeben. Wir können aus dieser Gleichung also noch keine Unbekannte bestimmen. Demnach betrachten wir als nächstes die Momentengleichgewichtsbedingung und wählen den Bezugspunkt so, dass eine unbekannte Kraft aus der Berechnung herausfällt. Dazu legen wir den Bezugspunkt genau in den Angriffspunkt der unbekannten Kraft. Wir wählen beliebig das Lager A:

$\sum M_i^A = 0: \; \; B \cdot 4m - F \cdot 6m = 0$

Wir lösen die obige Gleichung nach der Auflagerkraft B auf:

$B = \dfrac{F \cdot 6m}{4m}$

Einsetzen der gegeben Werte führt uns zu:

$B_v = \dfrac{50 kN \cdot 6m}{4m} = 75 kN$

Die Auflagerkraft B muss insgesamt 75 kN aufnehmen, damit das Fachwerk sich nicht vertikal verschiebt.

Um herauszufinden wie viel die Auflagerkraft A_v aufnehmen muss, können wir nun die vertikale Gleichgewichtsbedingung heranziehen und nach A_v auflösen:

$A_v + B - F = 0$

$A_v = -B + F = -75 kN + 50 kN = -25 kN$

Die Auflagerkraft A_v muss -25 kN aufnehmen, damit sich das Fachwerk nicht vertikal verschiebt. Das negative Vorzeichen gibt an, dass die Auflagerkraft entgegen der angenommenen Richtung nach unten gerichtet ist. Für die weiteren Berechnungen gehen wir aber weiterhin von einer nach oben gerichteten Auflagerkraft A_v aus und müssen somit das negative Ergebnis verwenden.

Zusammenfassung der Auflagerkräfte:

Auflagerkraft	A_v	A_h	B
Betrag	-25 kN	0	75 kN

Ritterschnitt: Stabkräfte berechnen

Im obigen Fachwerk sind nach den drei bekannten Regeln keine Nullstäbe vorab ermittelbar. Es können trotzdem bei der Berechnung Nullstäbe auftreten.

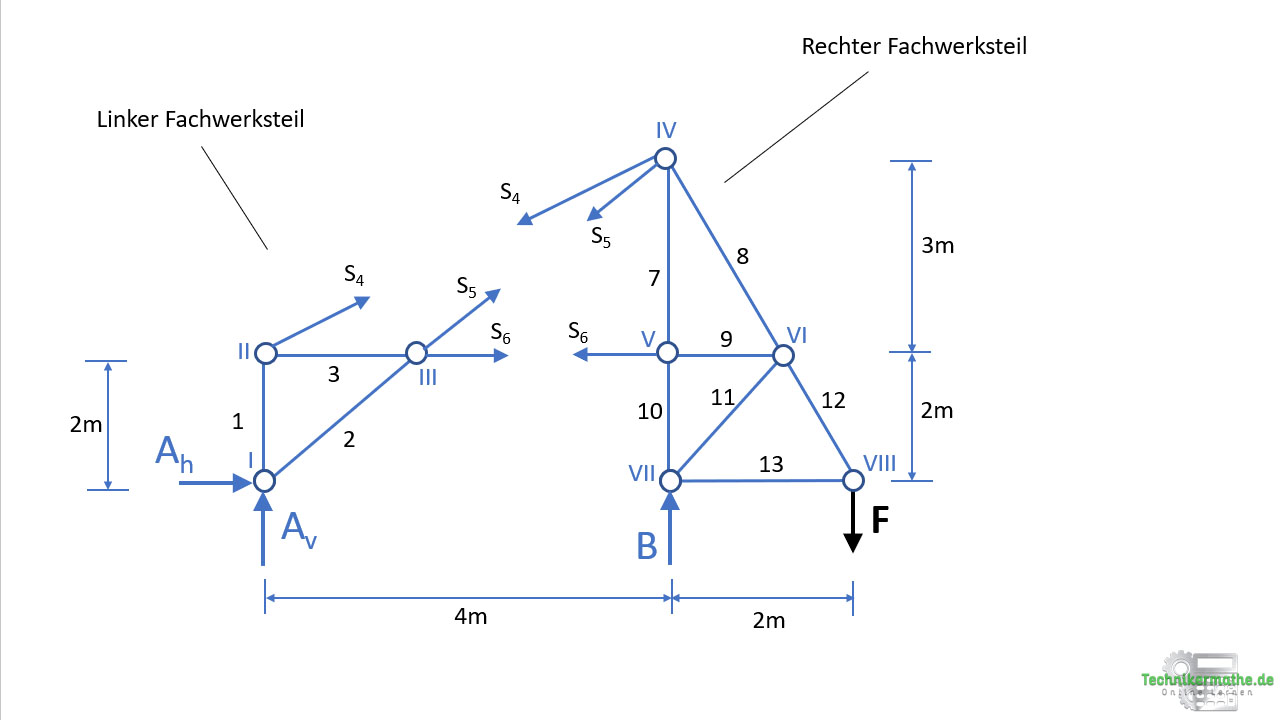
Wir führen als nächstes einen Schnitt durch die drei gesuchten Stäbe durch. Diese liegen nicht alle in einem Knoten und teilen das Fachwerk in zwei Teile:

Schnitt durch drei Stäbe, Ritterschnittverfahren, Fachwerk, Wie wird beim Ritterschnittverfahren geschnitten?, drei Stäbe, Knoten — Schnitt durch das Fachwerk

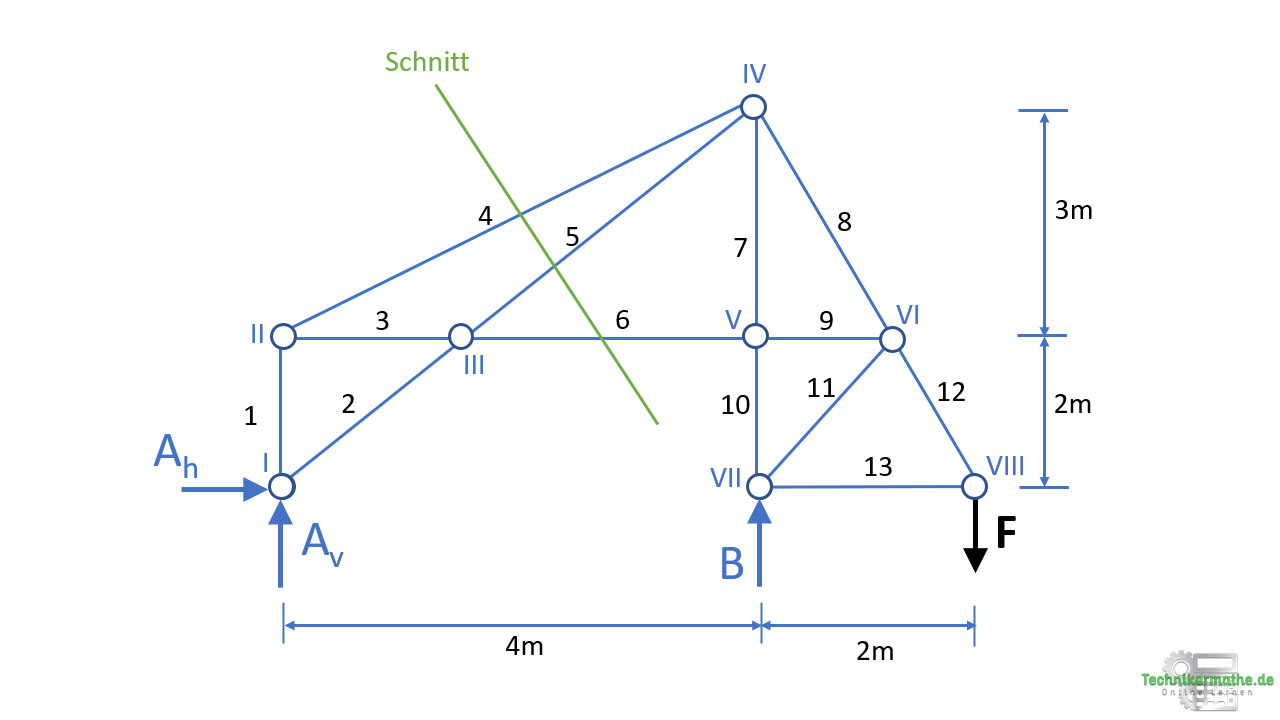
Nach dem Schnitt liegen die drei unbekannten Stabkräfte frei:

Ritterschnittverfahren, Beispiel, Stabkräfte, Zugkräfte — Stabkräfte als Zugkräfte

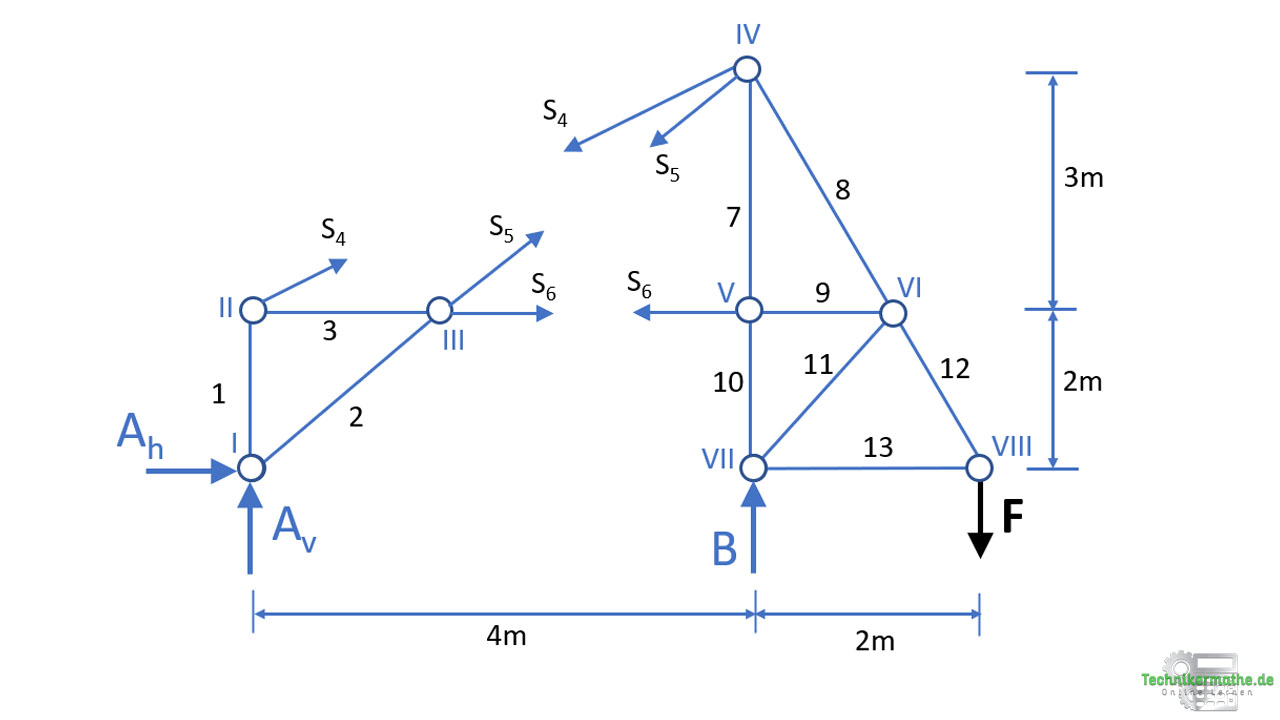
Nachdem die gesuchten drei Kräfte frei liegen, wollen wir diese als nächstes berechnen. Dazu können wir je Fachwerksteil die drei Gleichgewichtsbedingungen in der Ebene heranziehen. Wichtig ist, dass wir hier die beiden Fachwerksteile separat betrachten.

Bestimmung der Winkel mittels Trigonometrie

Bevor wir allerdings mit der Berechnung beginnen können, sollten wir zunächst die Winkel von den gesuchten Stabkräften zur Waagerechten bestimmen. Dazu konstruieren wir rechtwinklige Dreiecke so, dass wir die Trigonometrie am rechtwinkligen Dreieck anwenden können. Wir müssen dafür die gegebenen Abmessungen heranziehen.

Wir starten mit dem Winkel zur Waagerechten des Stabs S₅:

Ritterschnittverfahren, Trigonometrie, Winkel, Tangens, Fachwerk — Trigonometrie am rechtwinkligen Dreieck

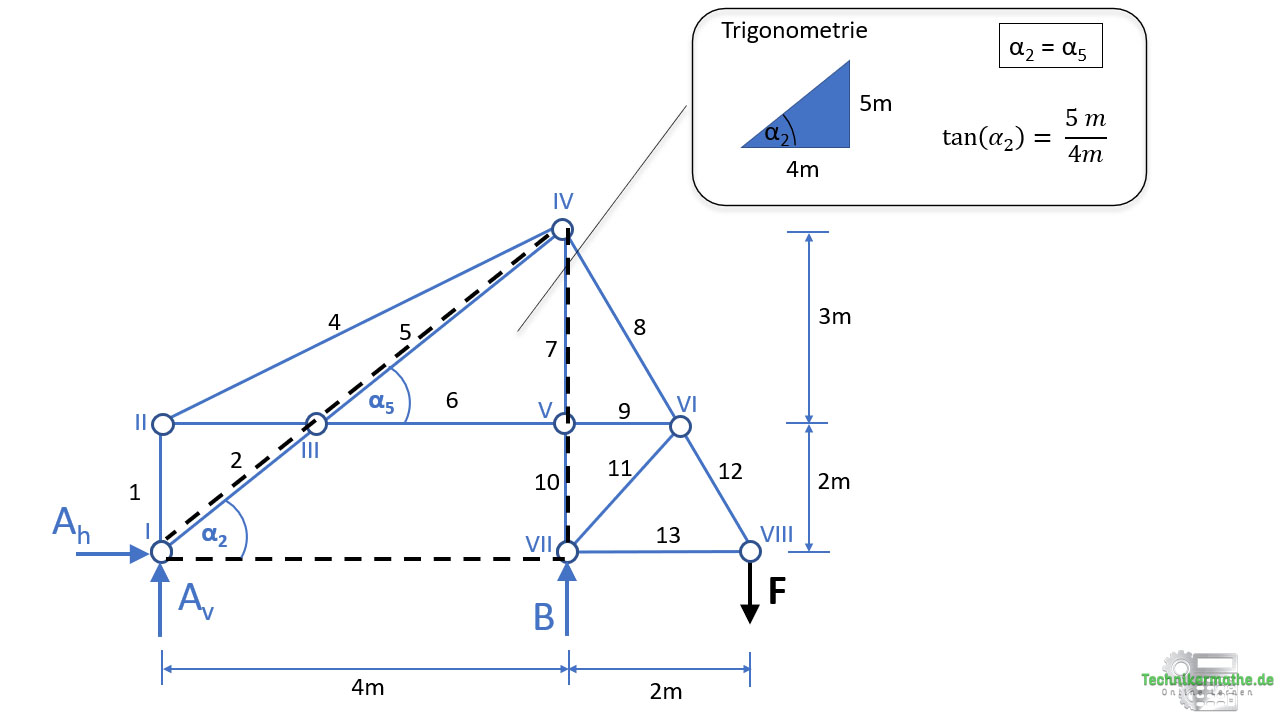
Wir betrachten das obige rechtwinklige Dreieck (gestrichelte Linien) um zunächst den Winkel α₂ zu bestimmen. Dieser Winkel ist identisch zum Winkel α₅, da beide Stäbe auf derselben Wirkungslinie liegen. Wir können hier den Tanges anwenden, da Gegenkathete und Ankathete des rechtwinkligen Dreiecks (rechter Winkel im Knoten VII) gegeben sind:

$\tan(\alpha_2) = \dfrac{\text{Gegenkathete}}{\text{Ankathete}}$

Die Gegenkathete ist die Höhe mit 5m, die Ankathete die Länge mit 4m:

$\tan(\alpha_2) = \dfrac{5m}{4m}$

Wir lösen nach dem gesuchten Winkel auf:

$\alpha_2 = tan^{-1}(\dfrac{5m}{4m})$

$\alpha_2 = \alpha_5 = 51,34 ^{\circ}$

Hinweis!

Die Berechnungen von Winkel und Seiten eines rechtwinkligen Dreiecks werden ausführlich in unserem Onlinkurs Ph1 – Grundlagen der Physik behandelt.

Als nächstes betrachten wir den Winkel vom Stab S₄ zur Waagerechten und betrachten dabei das folgende rechtwinklige Dreieck:

Auch hier wenden wir den Tangens an:

$\tan(\alpha_4) = \dfrac{3m}{4m}$

Auflösen nach dem gesuchten Winkel:

$\alpha_4 = \tan^{-1}(\dfrac{3m}{4m})$

$\alpha_4 = 36,87^{\circ}$

Unbekannte Stabkräfte bestimmen

Wir kommen nun wieder zurück zum freigeschnittenen Fachwerk, um die drei Stabkräfte an den beiden Fachwerksteilen zu berechnen. Zur Berechnung der Stabkräfte stehen uns die drei Gleichgewichtsbedingungen der Ebene zur Verfügung.

Beim Ritterschnittverfahren ist es in jedem Fall sinnvoll mit der Momentengleichgewichtsbedingung zu starten.

Für die Momentengleichgewichtsbedingung müssen wir einen Bezugspunkt wählen. Diesen müssen wir so festlegen, dass so viele unbekannte Stabkräfte wie möglich bei der Berechnung wegfallen. In diesem Fall also zwei unbekannte Stabkräfte, damit aus der Momentengleichgewichtsbedingung eine unbekannte Stabkraft berechnet werden kann.

Merk’s dir!

Stabkräfte fallen dann innerhalb der Momentengleichgewichtsbedingung heraus, wenn das Moment welches sie ausüben gleich Null ist (M = F ⋅ h = 0). Dies ist dann gegeben, wenn die Wirkungslinien der Stabkräfte den Bezugspunkt schneiden!

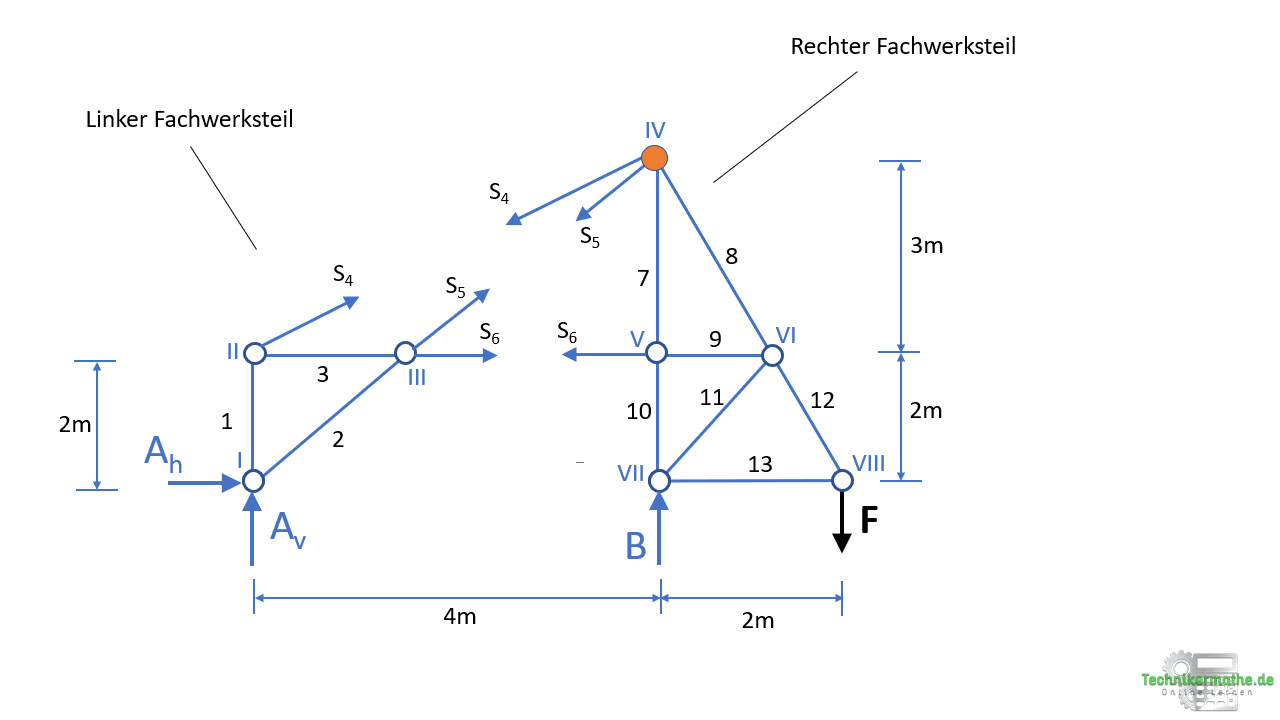
Wir legen dazu den Bezugspunkt in den Knoten IV (rechter Fachwerksteil):

Momentengleichgewichtsbedingung (rechter Fachwerksteil)

Wir können nun die Momente bestimmen, welche die Kräfte auf den Bezugspunkt ausüben. Dabei bleiben wir am rechten Fachwerksteil, weil dort der Bezugspunkt liegt. Die Stabkräfte S₄ und S₅ fallen weg, da diese den Bezugspunkt schneiden. Es verbleibt eine unbekannte Stabkraft S₆ sowie die gegebene äußere Kraft F. Die Wirkungslinie der Auflagerkraft B schneidet den Bezugspunkt, weshalb auch diese kein Moment ausübt und damit wegfällt.

$\sum M_i^{(IV)} = 0: \; \; -S_6 \cdot 3m - F \cdot 2m = 0$

Auflösen nach der unbekannten Stabkraft S₆:

$-S_6 \cdot 3m - F \cdot 2m = 0$

$S_6 \cdot 3m = - F \cdot 2m$

$S_6 = -\dfrac{F \cdot 2m}{3m}$

Einsetzen von F = 50 kN ergibt:

$S_6 = -\dfrac{50 kN \cdot 2m}{3m} = -33,33 kN$ (Druckkraft)

Gleichgewichtsbedingung in x-Richtung (rechter Fachwerksteil)

Wir haben nun schon eine unbekannte Stabkraft bestimmt. Als nächstes können wir die Gleichgewichtsbedingung in x-Richtung anwenden:

$\sum F_{ix} = 0: \; \; -S_4 \cdot \cos(\alpha_4) - S_5 \cdot \cos(\alpha_5) - S_6 = 0$

Einsetzen der berechneten Winkel zur Waagerechten und berechnen des Kosinus:

$-S_4 \cdot \cos(36,87^{\circ}) - S_5 \cdot \cos(51,34 ^{\circ}) - S_6 = 0$

$-S_4 \cdot 0,8 - S_5 \cdot 0,625 - S_6 = 0$

Einsetzen der berechneten Stabkraft S₆:

$-S_4 \cdot 0,8 - S_5 \cdot 0,625 - (-33,33 kN)= 0$

(I) $-S_4 \cdot 0,8 - S_5 \cdot 0,625 + 33,33 kN= 0$

In der obigen Gleichung sind zwei unbekannte Stabkräfte gegeben. Wir können hier also noch keine unbekannte Kraft berechnen, da pro Gleichgewichtsbedingung nur eine unbekannte Kraft berechnet werden kann.

Vertikale Gleichgewichtsbedingung (rechter Fachwerksteil)

Wir betrachten als nächstes die vertikale Gleichgewichtsbedingung und berücksichtigen am rechten Fachwerksteil alle vertikalen Kräfte:

$\sum F_{iy} = 0: \; \; B - F - S_4 \cdot \sin(\alpha_4) - S_5 \cdot \sin(\alpha_5) = 0$

Einsetzen der Winkel:

$B - F - S_4 \cdot \sin(36,87^{\circ}) - S_5 \cdot \sin(51,34 ^{\circ}) = 0$

Einsetzen der äußeren Kräfte:

$75kN - 50kN - S_4 \cdot \sin(36,87^{\circ}) - S_5 \cdot \sin(51,34 ^{\circ}) = 0$

Berechnung des Sinus’:

(II) $25 kN - S_4 \cdot 0,6 - S_5 \cdot 0,781 = 0$

Hier haben wir nun zwei unbekannte Kräfte gegeben. Wir können nun eine der beiden Gleichungen (I) oder (II) nach einer unbekannten auflösen und in die andere Gleichung einsetzen.

Wir lösen die Gleichung (II) nach der Stabkraft S₄ auf:

(II) $25 kN - S_4 \cdot 0,6 - S_5 \cdot 0,781 = 0$

$S_4 \cdot 0,6 = 25 kN - S_5 \cdot 0,781$

$S_4 = \dfrac{25 kN - S_5 \cdot 0,781}{0,6}$

$S_4 = 41,667 kN - S_5 \cdot 1,302$

Einsetzen in Gleichung (I) und nach S₅ auflösen:

$-S_4 \cdot 0,8 - S_5 \cdot 0,625 + 33,33 kN= 0$

$-(41,667 kN - S_5 \cdot 1,302) \cdot 0,8 - S_5 \cdot 0,625 + 33,33 kN= 0$

$-33,33 kN + S_5 \cdot 1,042 - S_5 \cdot 0,625 + 33,33 kN = 0$

$S_5 \cdot 1,042 - S_5 \cdot 0,625 = 0$

$S_5 \cdot 0,417 = 0$

$S_5 = 0$ (Nullstab)

Wir können nun noch die Stabkraft S₄ aus der nach S₄ aufgelösten Gleichung II bestimmen:

$S_4 = 41,67 kN - S_5 \cdot 1,302$

$S_4 = 41,67 kN - 0 \cdot 1,302$

$S_4 = 41,67 kN$ (Zugstab)

Wir haben nun alle Stabkräfte am rechten Fachwerksteil berechnet. In der Tabelle sehen wir nochmal die Zusammenfassung der Stabkräfte:

Stab	S₄	S₅	S₆
Betrag	41,67 kN	0 kN	33,33 kN
Richtung	Zugstab	Nullstab	Druckstab

Merk’s dir!

Welchen Fachwerksteil wir zur Berechnung der Stabkräfte verwenden ist unerheblich. Wir können auch zwischen den beiden Fachwerksteilen wechseln, wenn das notwendig oder einfacher für die Berechnungen ist. Wir müssen aber beachten, dass innerhalb einer Gleichgewichtsbedingung auch nur Kräfte aus einem Fachwerksteil berücksichtigt werden dürfen.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++