MA1 – Zahlenmengen [Erklärungen, Beispiele]

In dieser Lerneinheit wollen wir uns die unterschiedlichen Zahlenmengen anschauen.

Für ein optimales Verständnis helfen dir mehrere ausführliche Beispiele mit Zahlenwerten zu dem Thema.

Dieser Lerntext ist ein Auszug aus unserem Onlinekurs MA1 – Vorkurs Mathe.

Zahlenmengen – Grundlagen

Wir unterscheiden die folgenden Zahlenmengen voneinander:

Natürliche Zahlen
Ganze Zahle
Rationale Zahlen
Reelle Zahlen
und komplexe Zahlen.

Schauen wir uns im Folgenden die Zahlenmengen mal genauer an.

Video: Zahlenmengen

Im folgenden Video zeigen wir euch nochmal die Zahlenmengen auf.

Natürliche Zahlen

Natürliche Zahlen sind alle ganzen Zahlen von $0$ bis $\infty$ (unendlich). Dabei werden nur ganze positive Zahlen zu den natürlichen Zahlen gezählt.

Beispiel!

Natürliche Zahlen sind zum Beispiel: 0 / 1 / 5 / 350 / 1025 / 1.000.001

Die natürlichen Zahlen werden mit dem Formelzeichen $\mathbb{N}$ angegeben. Wird die Null nicht hinzugezählt, so wählt man für die natürlichen Zahlen ohne Null das Formelzeichen $\mathbb{N}^*$ .

Addition und Subtraktion von natürlichen Zahlen

Für die natürlichen Zahlen ist die Addition und Multiplikation uneingeschränkt durchführbar:

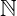$\mathbb{N}$ ist bezüglich der Addition und der Multiplikation abgeschlossen.
Alle anderen Rechenoperationen sind nicht uneingeschränkt durchführbar.

Abgeschlossenheit bedeutet, dass das Ergebnis der Berechnung innerhalb des Zahlenbereichs liegt. Werden also zwei natürliche Zahlen miteinander addiert oder multipliziert, so ergibt sich als Ergebnis auch eine natürliche Zahl. Bei den anderen Rechenoperationen wie der Subtraktion und der Division ist dies nur eingeschränkt möglich. Bei diesen Rechenoperationen ergibt sich nicht immer eine natürliche Zahl.

Beispiel: Abgeschlossenheit

Die natürlichen Zahlen 5 und 2 sollen miteinander addiert und multipliziert werden:

$5 + 2 = 7$ Ergebnis ergibt eine natürliche Zahl

$5 \cdot 2 = 10$ Ergebnis ist eine natürliche Zahl

Betrachten wir als nächstes die Subtraktion:

$5 - 2 = 3$ In diesem Fall ergibt sich ebenfalls eine natürliche Zahl. Betrachten wir nun aber:

$2 - 5 = -3$ so ist das Ergebnis eine negative Zahl und damit nicht innerhalb der natürlichen Zahlen. Es ist also deutlich zu erkennen, dass die Subtraktion der natürlichen Zahlen nur eingeschränkt möglich ist.

Betrachten wir nun die Division:

$\frac{5}{2} = 2,5$ Das Ergebnis ist keine natürliche Zahl. Genauso sieht es aus für

$\frac{2}{5} = 0,4$ .

Es gibt aber auch hier Brüche, die als Ergebnis eine natürliche Zahl aufweisen:

$\frac{2}{1} = 2$ .

Auch hier gilt, dass die Division nur eingeschränkt möglich ist.

Ganze Zahlen

Die ganzen Zahlen stellen eine Erweiterung der natürlichen Zahlen dar. Hier werden zusätzlich noch die ganzen negativen Zahlen, also Zahlen kleiner Null mitberücksichtigt.

Beispiel!

Ganze Zahlen sind zum Beispiel: -501 / -23 / -1 / 0 / 5 / 300 / 5.020

Die ganzen Zahlen werden mit dem Formelzeichen $\mathbb{Z}$ angegeben. Auch hier kann die Null ausgeschlossen werden, dann wählt man das Formelzeichen $\mathbb{Z}^*$ .

Für die ganzen Zahlen ist die Addition, Subtraktion und Multiplikation uneingeschränkt durchführbar:

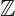$\mathbb{Z}$ ist bezüglich der Addition, Subtraktion und der Multiplikation abgeschlossen.
Alle anderen Rechenoperationen sind nicht uneingeschränkt durchführbar.

Rationale Zahlen

Die rationalen Zahlen sind die Erweiterung der ganzen Zahlen um negative und positive Brüche. Rationale Zahlen sind also alle ganzen Zahlen plus aller endlichen und unendlich periodischen Dezimalzahlen.

Beispiel!

Rationale Zahlen sind zum Beispiel:

$3,75 = \frac{15}{4}$

$0,1\overline{6} = \frac{1}{6}$

$-0,125 = \frac{1}{8}$

Die rationalen Zahlen werden mit dem Formelzeichen $\mathbb{Q}$ angegeben. Soll die Null hier nicht berücksichtigt werden, so gilt $\mathbb{Q}^*$ .

Für die rationalen Zahlen ist die Addition, Subtraktion, Division und Multiplikation uneingeschränkt durchführbar:

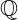$\mathbb{Q}$ ist bezüglich der Addition, Subtraktion, Division und der Multiplikation abgeschlossen.
Das Wurzelziehen ist hier nicht uneingeschränkt durchführbar.

Reelle Zahlen

Reelle Zahlen umfassen sowohl die rationalen Zahlen (als Bruch darstellbar: endlich oder periodisch) sowie die irrationalen Zahlen (nicht als Bruch darstellbar; unendlich viele, nicht periodische Nachkommastellen).

$\mathbb{R} = \mathbb{Q} + \mathbb{I}$

Beispiel!

Bekannte Beispiele für irrationale Zahlen sind $\sqrt{2} = 1,4142...$ und die Kreiszahl $\pi = 3,1415...$ . Diese Zahlen sind nicht als Bruch darstellbar und haben unendlich viele, nicht periodische Nachkommastellen. Hingegen ist $\frac{1}{3}$ als Bruch darstellbar und periodisch und gehört deswegen den rationalen Zahlen an.

Die reellen Zahlen werden mit dem Formelzeichen $\mathbb{R}$ angegeben. Soll die Null hier nicht berücksichtigt werden, so gilt $\mathbb{R}^*$ .

Für die reellen Zahlen ist die Addition, Subtraktion, Division, Multiplikation und das Wurzelziehen einer positiven Zahl uneingeschränkt durchführbar:

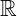$\mathbb{R}$ ist bezüglich der Addition, Subtraktion, Division, Multiplikation und Wurzelziehen abgeschlossen.
Das Wurzelziehen einer negativen Zahl ist hier nicht durchführbar.

Die reellen Zahlen sollen in der folgenden Tabelle nochmals mit unterschiedlichen Bezeichnungen angegeben werden. Dabei können die reelle Zahlen – je nach Bezeichnung – gewissen Beschränkungen unterliegen. So bedeutet $\mathbb{R^*}$ zum Beispiel, dass alle reelle Zahlen außer die Null betrachtet werden.

Alle reellen Zahlen	$\mathbb{R}= \{ x \| \text{ x ist eine rationale oder irrationale Zahl} \}$
Reelle Zahlen ohne Null	$\mathbb{R}= \{ x \| x \not 0 \; \text{und} \; x \in \mathbb{R} \}$
Nicht negative reelle Zahlen	$\mathbb{R}_+ = \{ x \| x \ge 0 \; \text{und} \; x \in \mathbb{R} \}$
Nicht negative reelle Zahlen ohne Null	$\mathbb{R}^*_+ = \{ x \| x > 0 \; \text{und} \; x \in \mathbb{R}\}$
Nicht positive reelle Zahlen	$\mathbb{R}_- = \{ x \| x \le 0 \; \text{und} \; x \in \mathbb{R} \}$
Nicht positive reelle Zahlen ohne Null	$\mathbb{R}^*_- = { x \| x < 0 \; \text{und} \; x \in \mathbb{R}\}$

Komplexe Zahlen

Komplexe Zahlen hingegen erfassen die Wurzel aus negativen Zahlen. Dies ist nur möglich durch Einführung einer widerspruchsfreie Definition, damit die bisher gültigen Rechenregeln nicht verletzt werden. Verwendet hierfür wird:

Komplexe Zahlen

$i = \sqrt{-1}$

$\rightarrow i \cdot i = i^2 = -1$

Innerhalb der Elektrotechnik wird als Symbol statt $i$ ein $j$ benutzt, um eine Verwechslung mit dem Momentanwert der Stromstärke $i(t)$ zu vermeiden. Die komplexen Zahlen werden mit den Zeichen $\mathbb{C}$ angegeben.

Realteil und Imaginärteil von komplexen Zahlen

Die komplexen Zahlen bestehen aus einem Realteil $z := x$ und einem Imaginärteil $z := y$ .

$\mathbb{C} := \{x + iy \; \; |x,y \in \mathbb{R}\}$

Innerhalb eines x,y-Koordinatensystems stellt die $x$ -Achse die reelle Achse und die $y$ -Achse die imaginäre Achse dar.

Beispiel: Realteil und Imaginärteil

Beispiel!

Es sei die folgende komplexe Zahl gegeben: $z = 4 + i \cdot 3$ .

Was ist der Real- und was der Imaginärteil?

Die komplexe Zahl $z = 4 + i\cdot 3$ hat den Realteil $z = 4$ und den Imaginärteil $z = 3$ .

Eine komplexe Zahl die keinen Imaginärteil besitzt kann man mit den reellen Zahlen identifizieren. Eine komplexe Zahl die keinen Realteil besitzt wird als rein-imaginär bezeichnet.

Die komplexe Zahl $z = \frac{1}{5} + 0 \cdot i$ entspricht der reellen Zahl $\frac{1}{5}$ .

Die komplexe Zahl $z = i \cdot \frac{1}{8}$ ist rein-imaginär.

Was kommt als Nächstes?

In den nächsten Lektionen behandeln wir die Grundrechenarten.

Was gibt es noch bei uns?

Optimaler Lernerfolg durch tausende Übungsaufgaben

Übungsbereich (Demo) - Lerne mit mehr als 4000 Übungsaufgaben für deine Prüfungen

Quizfrage 1

“Wusstest du, dass unter jedem Kursabschnitt eine Vielzahl von verschiedenen interaktiven Übungsaufgaben bereitsteht, mit denen du deinen aktuellen Wissensstand überprüfen kannst?”

Alle Technikerschulen im Überblick

Zum Verzeichnis der Technikerschulen (Alles Rund um die Schulen) — Zum Verzeichnis der Technikerschulen

Kennst du eigentlich schon unser großes Technikerschulen-Verzeichnis für alle Bundesländer mit allen wichtigen Informationen (Studiengänge, Kosten, Anschrift, Routenplaner, Social-Media) ? Nein? – Dann schau einfach mal hinein:

Was ist Technikermathe?

Unser Dozent Jan erklärt es dir in nur 2 Minuten!

Oder direkt den > kostenlosen Probekurs < durchstöbern? – Hier findest du Auszüge aus Alle Onlinekurse Technikermathe!

Geballtes Wissen in derzeit 26 Kursen

Hat dir dieses Thema gefallen? – Ja? – Dann schaue dir auch gleich die anderen Themen zu den Kursen

WT3 (Werkstoffprüfung) und
TM1 (Technische Mechanik – Statik) an.

Lerne nun erfolgreich mit unserem Onlinekurs Technische Mechanik 1 — TM1 (Technische Mechanik)

Lerne nun erfolgreich mit unserem Onlinekurs Werkstofftechnik 3 — WT3 (Werkstoffprüfung)

Perfekte Prüfungsvorbereitung für nur 14,90 EUR/Jahr pro Kurs

++ Günstiger geht’s nicht!! ++

Oder direkt Mitglied werden und Alle unsere Onlinekurse (inkl. Webinare + Unterlagen) sichern ab 7,40 EUR/Monat ++ Besser geht’s nicht!! ++